基于对偶变量变分原理的完整约束系统保辛算法
满淑敏, 高 强, 钟万勰
(大连理工大学 工业装备结构分析国家重点实验室,工程力学系,大连 116023)
1 引 言
哈密顿系统的一个主要性质是其相流保持辛结构[1,2],因此其近似积分的数值方法也应该具有保辛的性质[3]。在完整约束哈密顿动力系统中,约束的存在给数值积分带来了许多问题。如一些传统算法在处理完整约束系统时,约束不是直接施加,而是由等价的加速度约束所代替。在这个过程中,数值积分带来的误差会使得结果无法满足系统原有的约束条件,导致硬曲面下沉这种不真实现象的产生。为解决这类误差,引入了复原力的概念,但这类任意添加的参数必须要根据每一个计算过程进行调整,并要引入人工的能量损失。对于高度受限的系统,这类损失在最终所生成的动力系统中将占据支配作用[4]。而保辛算法能保持系统的固有特性,其数值结果具有能量和动量守恒等特点[5,6]。因此,研究完整约束系统的保辛算法具有重要意义。
变分积分法是构造保辛算法的一类重要手段[7,8]。在一类变量表示的拉格朗日体系内,利用哈密顿原理,文献[7,9]通过对作用量进行近似,给出了构造保辛算法的通用方法。文献[10]讨论了积分点个数与广义位移近似多项式阶数不相同时算法的收敛阶数。在完整约束系统中,为提高算法精度,Wenger等[11]同时使用Gauss积分和Lobatto积分,得到一种高精度的Galerkin变分积分法。
上述保辛算法都是基于拉格朗日函数构造的,但实际有些问题只能获得哈密顿函数,而无法给出拉格朗日函数。此时,保辛算法的构造基于对偶变量变分原理。在无约束哈密顿系统中,文献[12-15]基于两种不同的对偶变量变分原理,通过选取不同的独立变量,分别构造了四种不同类型的高阶保辛算法。这类保辛算法只需哈密顿函数便可实施,拓宽了保辛算法的应用领域。
本文从哈密顿函数表示的对偶变量变分原理出发,研究完整约束哈密顿动力系统的保辛算法。首先,引入拉格朗日乘子,得到包含完整约束方程的对偶变量变分原理;然后,选取积分区间两端位移为独立变量,基于变分原理的一种离散化形式,得到能够在位移插值点处高精度满足完整约束的高阶保辛算法。
2 完整约束哈密顿系统的基本方程和对偶变量变分原理
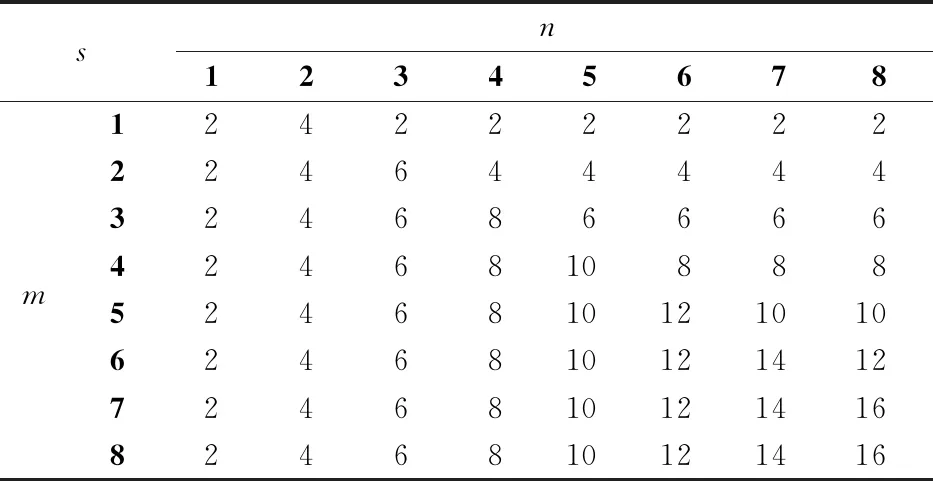
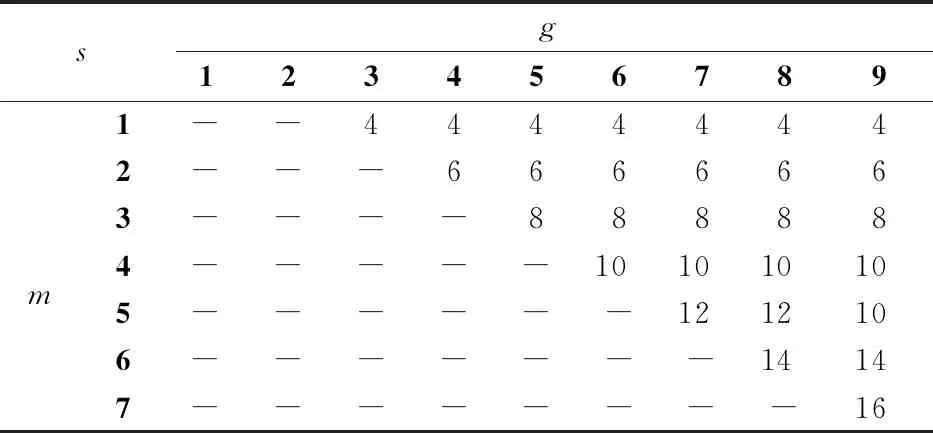
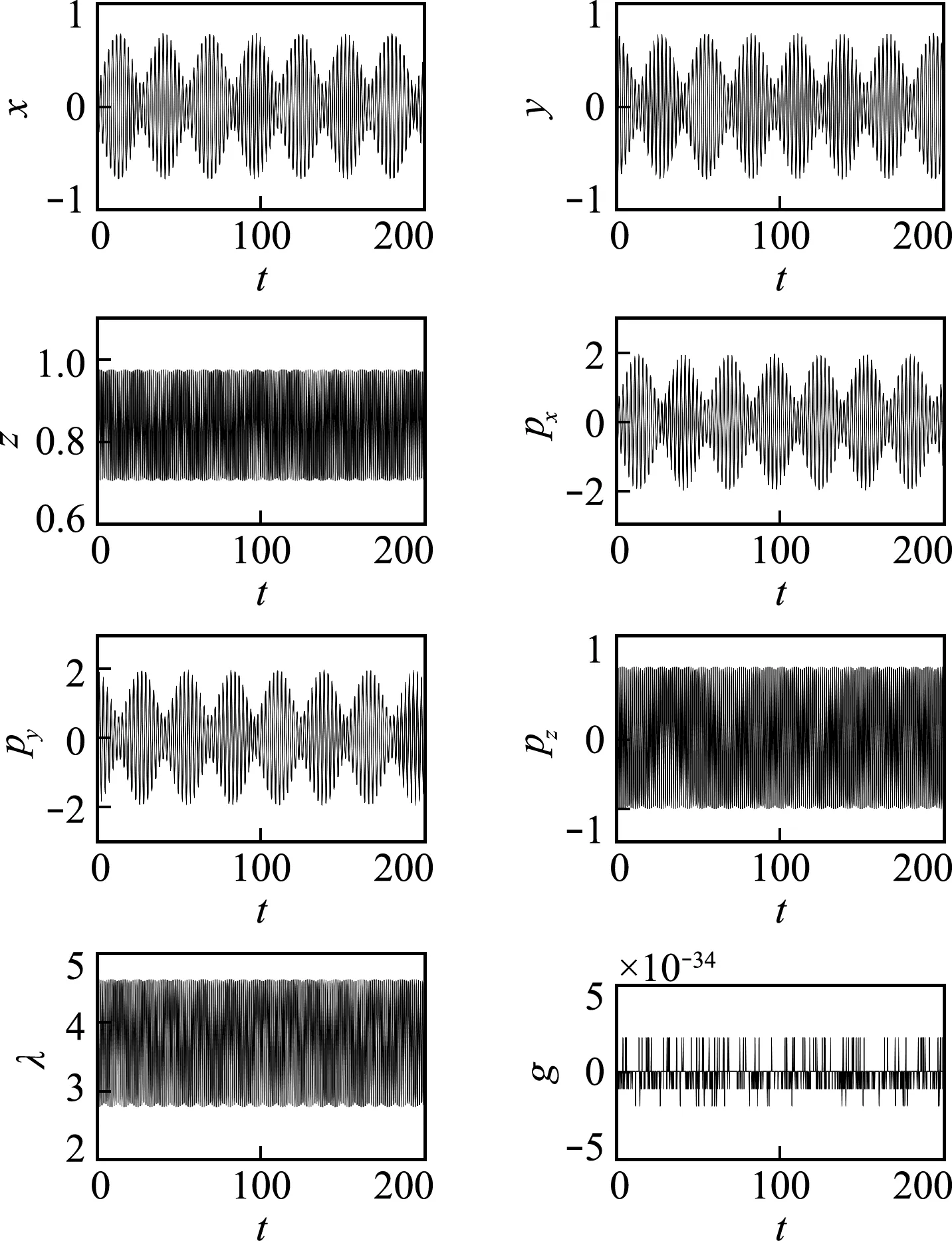
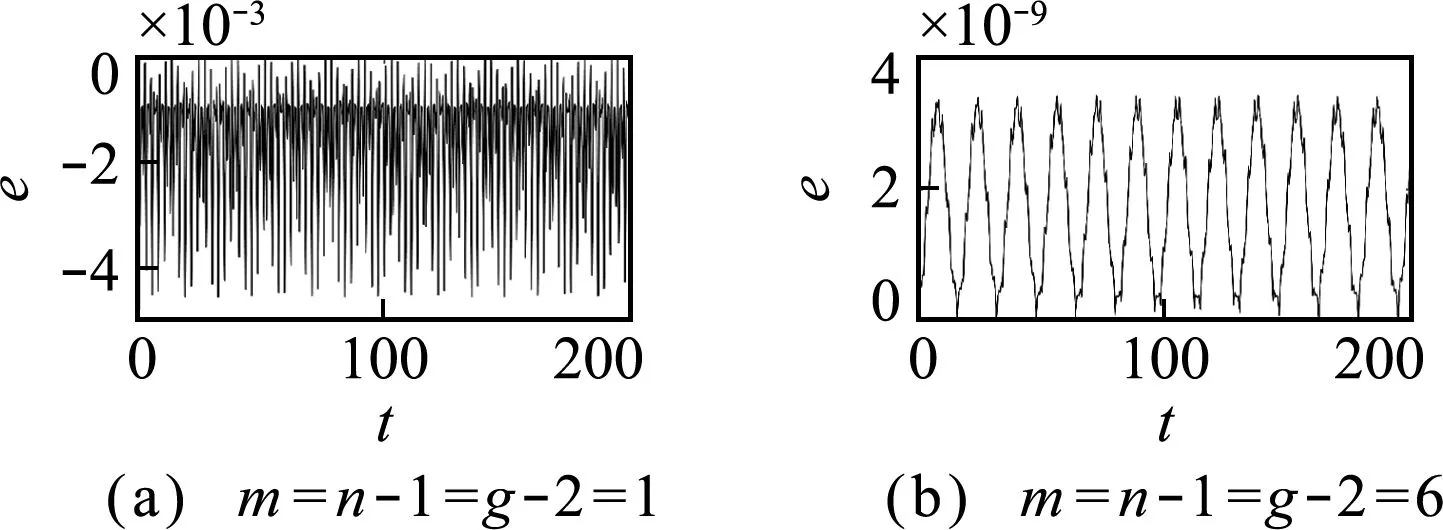
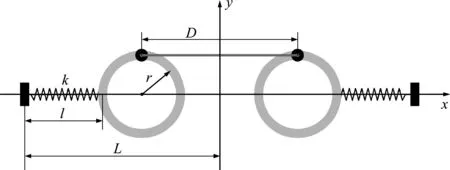
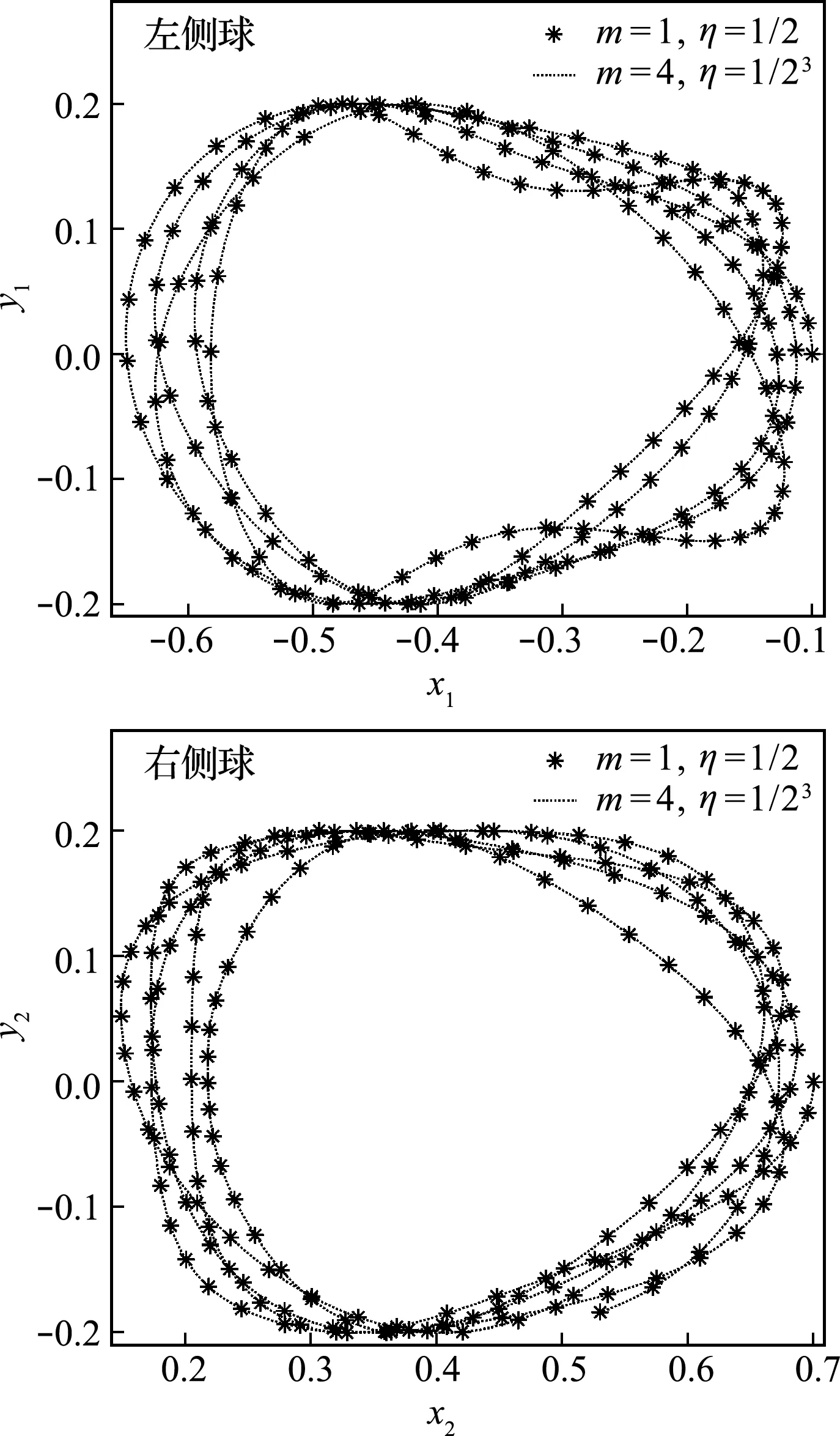
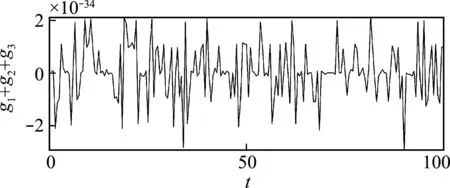
设哈密顿动力系统位置坐标由d维向量q= {q1,q2,…,qd}T表示,d维位置坐标受到c g(q) = {g1(q),g2(q),…,gc(q)}T=0 (1) 哈密顿原理表明,系统的运动方程可由变分方程(2)导出, (2) (3) 则由哈密顿函数表示的对偶变量变分原理为 (4) 完成方程(4)的变分得到 pT(t1)δq(t1)-pT(t0)δq(t0) (5) 式中G(q) = ∂g(q)/∂q。根据式(5),如果积分区间两端位移给定,则变分原理导出系统的运动方程为 (6) 如果系统的运动方程提前满足,则作用量仅仅是时间区间左右两端位置坐标的函数,即 δS=pT(t1)δq(t1)-pT(t0)δq(t0) (7) 方程(7)对应了q(t0),p(t0)和q(t1),p(t1)之间的一个正则变换 p(t0) =- ∂S[q(t0),q(t1)]/[∂q(t0)] p(t1) = ∂S[q(t0),q(t1)]/[∂q(t1)] (8) 式(8)可用于构造数值算法。本文将以方程(8)为出发点,构造完整约束哈密顿动力系统的保辛算法。 (9) (k= 0,1,…,n)(10) (k= 0,1,…,m)(11) (k= 0,1,…,z)(12) 将式(9)代入式(4),可得 (13) (14) 根据式(7),近似作用量仅为积分区间两端位移q0和qn的函数,对近似作用量变分可得 (i= 1,2,…,n-1)(15) (i= 0,1,…,m)(16) (i= 0,1,…,z)(17) 同时,根据正则变换(8)可得 ∂Sd/∂q0+p0=0, ∂Sd/∂qn-pm=0 (18) (19) 则式(14)的最后一项为 (20) (i= 1,2,…,n-1)(21) 方程(21)为约束方程在位移插值点处的表达式。需要注意的是,由于初值q0已知,初始点处的约束方程g(q0) =0自动满足,因此,需要另外补充c个方程。本文使用积分区间右端点处的速度约束作为补充方程。将约束方程(1)对时间求导,并利用式(6)可得右端点处的速度约束为 (22) 至此,求解方程组(15,16,18,21,22)便可得到完整约束哈密顿动力系统的解。本文采用牛顿迭代法求解。由于上述非线性方程组由对偶变量变分原理导出,因此算法为保辛算法。 通过两个算例分析保辛算法的数值性质。数值算例在64位计算机和64位操作系统下完成,程序使用Fortran实现,采用四倍精度。 算例1考虑三维球面摆在非线性势能场中的运动。三维球面摆摆长l=1.0 m,质量m=1.0 kg,位移与动量分别为q= {xyz}T和p= {pxpypz}T,系统哈密顿函数和约束方程为 (23) g(q) =x2+y2+z2-l2= 0 (24) 系统初始状态为 (25) 大量数值结果表明,当位移和动量的插值阶次分别为n和m时,算法所需最少Gauss积分点个数为g>max. (n,m),而当g≤max. (n,m)时,由于在牛顿迭代求解过程中雅可比矩阵奇异,因此不能求解。 (26) (27) 由表1可知,算法收敛阶数s满足如下规律, (28) 可见,位移和动量插值阶次的最佳搭配方案为n=m+1,此时算法的收敛阶数和计算效率最高。表2 给出了m和g取不同值,且n=m+1时,算法的收敛阶数。由表2可知,仅改变g的值不会改变算法的收敛阶数。综合表1和表2,位移的插值阶次n、动量的插值阶次m以及Gauss积分点个数g的最佳搭配方案为m=n-1 =g-2。此时,算法的收敛阶数为s= 2m+2。 表1 g= max. (n,m)+1,且n和m取不同值时保辛算法的收敛阶数 表2 n= m+1,且n,m和g取不同值时保辛算法的收敛阶数 算例2考虑一弹簧连杆装置。两个弹性系数为k,可以在光滑水平面上自由振动的弹簧分别将一端固定,另一端连接半径为r、质量为M的光滑圆环形轨道,轨道上各放置一质量为m的小球,两球在轨道中运动,同时又由一长为D的轻质细杆相连。两弹簧原长均为l,振动方向在同一直线上,固定端相距2L。建立图3所示坐标系,系统位移为q= {x1,y1,x2,y2,O1,O2}T, 动量为p= {px1,py1,px2,py2,pO1,pO2}T。 其中(x1,y1)和(x2,y2)分别为左右两侧小球的位置坐标,O1和O2分别为左右两侧轨道圆心的x轴坐标。系统的哈密顿函数及约束方程为 图1 三维球面摆数值积分结果 图2 三维球面摆哈密顿函数相对误差 k(L-l-r+O1)2/2+k(L-l-r-O2)2/2 (29) (30) 系统参数取M=1.5 kg,m=1.0 kg,k=0.6 N/m,L=1.0 m,l=0.4 m,r=0.2 m,D=0.8 m,初值选取 q(0) = {-0.1,0,0.7,0,-0.3,0.5}T p(0) = {0,0.05,0,-0.05,0,0}T (31) 数值结果表明,算法参数的最佳搭配方案为m=n-1 =g-2,此时,算法阶数为s= 2m+2。 图3 弹簧连杆装置 图4 弹簧连杆装置中两球运动轨迹 图5 弹簧连杆装置完整约束之和 本文选取积分区间两端位移为独立变量,将位移、动量及拉格朗日乘子分别采用拉格朗日多项式近似,对作用量中包含约束的积分项使用Lobatto积分近似,对作用量中不包含约束的积分项使用Gauss积分近似,从而得到近似作用量。然后,在此近似作用量的基础上,基于对偶变量变分原理,构造了求解约束哈密顿系统的高阶保辛算法。通过数值算例得到如下结论。 (1) 如果位移、动量和拉格朗日乘子的插值阶次分别为n,m和z,Gauss积分点个数为g,则本文算法所需最少Gauss积分点个数为g>max. (n,m)。 (2) 位移插值阶次、动量插值阶次以及Gauss积分点个数的最佳搭配方案为m=n-1 =g-2。此时,算法的收敛阶数为s= 2m+2。 (3) 算法在位移插值点处高精度地满足完整约束方程。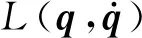
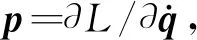
3 完整约束哈密顿系统的保辛算法
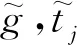

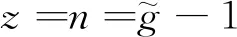
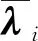
4 数值算例

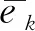
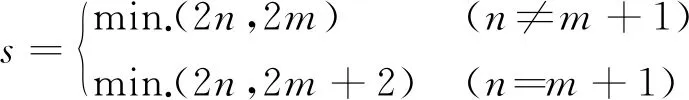

5 结 论

