考虑周长约束的圆柱薄壳初始几何缺陷随机场建模方法

李建宇， 魏凯杰

(天津科技大学 机械工程学院，天津市轻工与食品工程机械装备集成设计与在线监控重点实验室，天津 300222)

1 引 言

圆柱薄壳由于其优越的承载性能和简易的制造工艺，在航空航天、军事导弹和液罐存储等现代工程中广泛应用[1,2]。当圆柱薄壳的主要服役工况为轴压时，其失效模式为屈曲失稳。大量实践和研究表明[3-5]，圆柱薄壳的屈曲载荷对其在制造、安装和服役等环节产生的缺陷极其敏感，而这些缺陷的不确定性和薄壁结构稳定性分析中的非线性导致定量研究圆柱薄壳屈曲载荷的缺陷敏感性极具挑战，一直以来都受到学术界和工程界的广泛关注。

对圆柱薄壳屈曲载荷有影响的缺陷主要包括几何缺陷、刚度缺陷和边界缺陷，其中几何缺陷的影响最大。几何缺陷形状的表征是量化研究圆柱薄壳屈曲载荷缺陷敏感性的关键。常用的几何缺陷表征方法可划分为确定性方法和不确定性方法两类，其中确定性方法有实测缺陷法[6]、特征模态缺陷法[7]以及基于最优搜索的最不利缺陷多点扰动载荷法[8]等。不确定性方法有基于概率框架的随机场模型[9-12]和基于非概率框架的区间类方法[13,14]。由于缺陷的产生和分布具有事先不可预知性，因而采用不确定性方法表征缺陷应该是更自然的选择[15]。研究表明[10,16]，对于特定制造工艺和服役环境下的薄壁圆壳，其几何缺陷具有统计学规律，可以用随机过程等概率方法表征。与区间类方法相比较，利用随机场模型表征初始缺陷的好处是能够获得屈曲载荷的概率分布，从而为进一步的可靠性分析奠定基础，但随机场模型的构建需要更多的关于缺陷的先验信息。实测缺陷数据是当然的先验信息，如文献[9,10]利用实测缺陷数据拟合随机场模型中的参数(相关函数的方差和相关长度等)。除此之外，随机场所描述的物理量应该满足的物理条件也是一类有用的先验信息(如杨氏模量非负的条件)，为此文献[17]研究了如何将物理约束信息用于随机模型的构建中。圆柱薄壳几何缺陷虽具有不确定性，但其随机变化也受到相关物理约束。如薄壁圆柱壳除非受到内外压力作用并产生环向的总体塑性变形，否则其几何缺陷并不会引起圆柱周长的显著变化。本文研究发现，单纯利用二维高斯随机场表征圆柱薄壳的几何缺陷时，确实会出现圆柱周长显著增大或减小的情形，从而增大随机屈曲分析结果的分散性。为此，本文将讨论在几何缺陷的随机场模型中如何引入这一内在的物理约束条件，从而构建更符合实际的几何缺陷随机场模型。

在建立了几何缺陷的随机场模型后，就可以在结构稳定性分析模型的基础上利用不确定传播的办法获得屈曲载荷的概率分布。Monte Carlo法是最常用的不确定传播算法[18]，但其计算成本太高。近年来发展起来的多项式混沌展开法[19]，由于其较高的计算效率而受到广泛关注，在非线性结构分析、流固分析和多物理场分析等复杂问题的不确定性量化中广泛应用[20]。本文拟将其用于薄壁圆柱结构的随机屈曲分析。

2 初始几何缺陷的随机场建模

2.1 初始几何缺陷的先验分布

(1)

图1 圆柱薄壳结构及其展开

式(1)的协方差函数沿用了文献[9,10]的假设，即假定几何缺陷的随机场模型在轴向和环向的相关性相互独立，其中环向缺陷的相关性具有对称性。式中σ2表示随机场的方差，lx和ly分别为环向和轴向的相关长度参数。环向和轴向的协方差函数图像如图2所示。

2.2 引入周长不变约束

利用高斯随机场表征初始几何缺陷的优点是从数学上将可能发生的几何缺陷都涵盖在内，但带来的问题是，随机场所表征的几何缺陷也包含了很多不符合实际的情形。如仅考虑环向缺陷，利用随机场离散化方法随机生成一族环向几何缺陷，发现所生成的几何缺陷中包含了圆周周长显著增大或缩小的情形，如图3(a)所示。从力学的角度，薄壁圆柱结构在加工、装配和运输过程中主要发生壳的局部弯曲变形，即使是发生局部平面变形(如凹陷)，也不会导致环向周长的显著膨胀或缩小。因而，随机场所表征的这种缺陷是不符合实际的，应予剔除。

本文构造如下优化问题，实现在几何缺陷高斯随机场中引入周长不变约束的目的。

(2)

(∀y∈ [0,H], ∀ω∈Ω)

(3)

图2 环向和轴向协方差函数

图3 几何缺陷形状示例

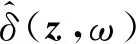
υL= (L-L0)/L0×100%

(4)

表1给出了随机抽样10次后圆周周长改变率的计算结果，保留四位有效数字，结果证明了周长不变约束的有效性。

2.3 随机场的离散化

(5)

对∀z∈ [0,2 πR]×[0,H]，求a(z)和b(z)，满足

表1 施加周长不变约束前后圆周周长变化率的数值试验结果

(6)

(7)

(8)

(9)

将式(8)代入优化问题(6)，利用罚函数法处理周长不变等式约束，并由该优化问题的一阶最优性条件得几何缺陷的随机变量表征。

(10)

(11)

式中I0= [0,0,…,0]1 × m，I1= [1,1,…,1]1 × m。式(10)将几何缺陷表达为一系列特定缺陷模式的随机组合。对于各阶缺陷模式，随着其阶数的增加，缺陷的波动性增加，如图4所示。

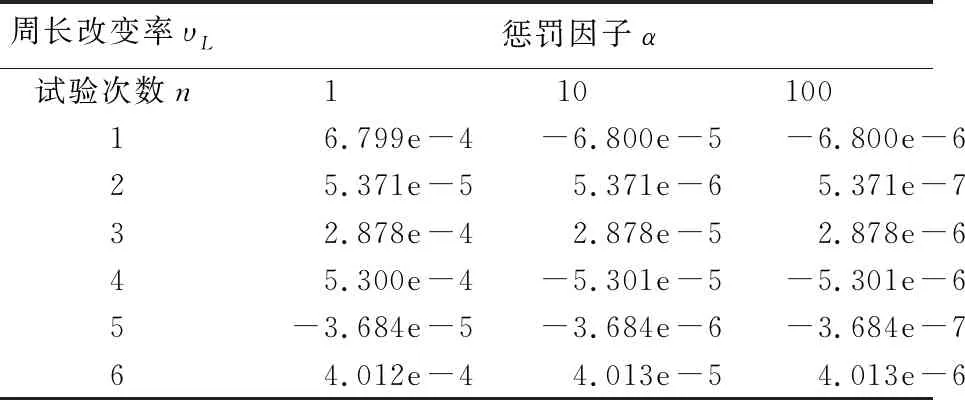
表2 惩罚因子对于周长改变率的影响

与现有文献关于几何缺陷随机场建模表征的两类方法[23]，即Gaussian随机场K-L展开法和谱展开方法相比，本文方法既具有K-L展开法在数值计算方面的优势，又满足谱展开法所具有的均值各态历经性。

3 基于多项式混沌展开法的随机屈曲分析

将初始几何缺陷表征为随机场(10)后，圆柱薄壳的几何参数中包含了独立高斯随机变量ξ∈ RN，其临界屈曲载荷Pc r也是一个随机变量，与随机变量ξ之间满足由屈曲分析模型决定的映射关系。为表述简单，将其表述为

Pc r= Μ(ξ)

(12)

对具有确定物理、几何和边界参数的圆柱薄壳结构，可以利用各类成熟的稳定性分析方法计算其临界屈曲载荷，包括特征值屈曲、显示动力学屈曲等非线性有限元分析方法[24,25]。屈曲分析模型给出了ξ与Pc r之间的隐式关系，但计算不方便而且成本昂贵。本文利用多项式混沌展开PCE(Polynomial Chaos Expansions)法构建Μ(·)的显式形式。

(13)

式中Φi(ξ)为关于高斯随机变量ξ的Hermite正交多项式，P= (d+p)!/d!p!，其中p为Hermite多项式Φ(ξ)的阶数，d为随机变量ξ的维数。ci∈ R为多项式系数，

式中E[Φi(ξ)Φj(ξ)] =δi j，E[Pc rΦj(ξ)] 表示Pc rΦj(ξ)的期望，需要做积分计算.为了减少积分点的数目，降低计算量，本文使用稀疏网格数值积分法求积，其中积分点上的Pc r值通过有限元方法进行计算，相关细节见文献[18,26]。

图4 不同阶的几何缺陷形状示例

4 数值算例

以一个光筒圆柱薄壳为例，说明本文方法的有效性。为简单而不失一般性，积分点上的屈曲载荷值的计算选用特征值屈曲分析方法。表3为模型参数，薄壳模型的一端固定，一端施加轴向单位外压载荷。采用S4R壳单元，进行收敛性分析后，将网格单元大小设为4 mm，如图5所示。具体计算时，将随机场的方差取为σ2= 4，相关长度取为lx= 0.6H，ly= 0.15L，利用式(10)得到随机的几何缺陷值，将其导入到有限元模型中进行积分点上屈曲载荷值的计算。

利用非干涉PCE构建代理模型(13)时，一旦选定稀疏网格精度水平k，就可确定积分点的数目，对积分点进行抽样计算，利用式(14)求得PCE系数，即可得到PCE代理模型。在PCE模型上进行有效的Monte Carlo模拟，便可估算薄壳结构屈曲载荷的统计特性。为了验证代理模型的精度，以直接Monte Carlo模拟1000次的计算结果为参考，计算不同精度水平下相对于MCS结果的误差，列入表4。

图5 完善薄壳的屈曲载荷收敛性分析

表3 模型参数

表4 不同精度水平下相对于MCS结果的误差

通过综合比较均值误差和方差误差，选定稀疏网格精度水平k= 3建立PCE模型。在对319个积分点进行抽样计算后，得到8阶的PCE模型。图6给出了在PCE模型上进行百万次抽样计算后，考虑周长不变约束和不考虑周长不变约束时圆柱薄壳屈曲载荷的统计结果。

将几何缺陷的不确定性表征为随机场后，屈曲载荷的结果为一个概率分布。从图6可知，是否引入周长不变约束，对于屈曲载荷的概率分布有明显的影响。首先，引入周长不变约束的屈曲载荷均值要比未引入约束的大，而方差比未引入约束的小。其原因是引入周长不变约束后，将不符合周长不变要求的随机缺陷剔除，从而减小了随机缺陷的样本总量范围，其分散性也就相应减小。另外，考虑到几何缺陷的幅值越小，相应屈曲载荷越大，引入周长不变约束会使得几何缺陷的幅值相对变小，相应的屈曲载荷均值也会增大。

为进一步说明引入周长不变约束的必要性和效果，研究随机场模型中的参数σ2和lx的变化对周长不变约束的敏感性。

图6带有几何缺陷的圆柱薄壳屈曲载荷统计直方图

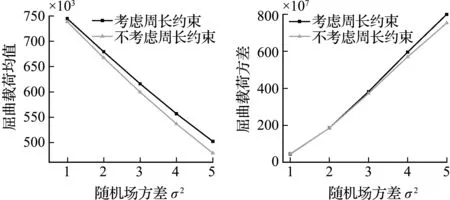
图7 随机场方差对屈曲载荷统计矩的影响(考虑和不考虑周长不变约束)

图7展示了随着随机场方差的变化，考虑周长不变约束和不考虑周长不变约束时的屈曲载荷的统计矩结果。可以看出，随着随机场方差的改变，几何缺陷考虑约束与否对屈曲载荷的均值和方差有差别，但是差别并不显著。因而，随机场模型中的方差参数对于约束的敏感性相对较小。

图8展示了随着随机场环向相关长度lx的改变，考虑周长不变约束和不考虑周长不变约束的屈曲载荷的统计矩结果变化。可以看出，环向相关长度对屈曲载荷的统计矩结果有较大影响，尤其当环向相关长度为0.25L时，随机模型中的环向相关长度参数对于周长不变约束的敏感性很强，是否考虑周长不变约束对于屈曲载荷的预测结果有很大影响。在协方差函数中，相关长度是对两点之间相互影响距离的度量。对于刚度较小的结构，如大型钢储罐，其相关长度相对较小，因而结构对周长不变约束并不敏感。对于刚度较大的圆柱薄壳结构，如加筋薄壳，其相关长度也较大，在利用随机场进行几何缺陷建模时，考虑周长不变约束显得尤为重要。

图8 环向相关长度对屈曲载荷统计矩的影响(考虑和不考虑周长不变约束)

5 结 论

本文采用随机场理论研究轴压圆柱薄壳结构屈曲载荷的几何缺陷敏感性。一方面，研究了圆柱薄壳结构初始几何缺陷的随机场建模方法，发现单纯将几何缺陷用二维高斯随机场表征时，在数学上会造成圆柱周长显著增大或缩小的几何缺陷。为了剔除这些不符合实际的几何缺陷，提出一种考虑周长不变约束的随机场建模方法，并通过数值试验表明了所提方法的必要性和有效性。另一方面，基于所建立的几何缺陷随机模型，提出利用非干涉混沌多项式展开法进行圆柱薄壳的随机屈曲分析，给出了临界屈曲载荷的概率分布，进而为进一步的可靠性分析和设计奠定了基础。