几何非线性分析的高效高阶无网格法

陈嵩涛， 段庆林， 马今伟

(大连理工大学 工业装备结构分析国家重点实验室，大连116023)

1 引 言

许多工程问题的力学分析需考虑结构构形的变化，如橡胶材料的大变形等。这一类问题的刚体转动和应变很剧烈，小变形假设失效，需要采用几何非线性模型进行计算。

传统有限元法的形函数依赖于网格单元，在处理几何非线性问题时容易因网格畸变而导致计算失败。与此不同，无网格法[1]的形函数仅依赖于离散点，无需网格单元，因而处理大变形问题更具优势。目前，无网格法已在几何非线性的数值分析中得到广泛应用[2-4]。

与线性分析不同，求解几何非线性问题时参考构形的选取关系到分析效率与结果的精确性，有限元通常选择相邻构形作为参考构形，即UL法，相比于有限元，无网格法求解形函数导数过程较为复杂，使用UL法不断更新构形，必然会降低计算效率。针对该问题，需要建立既能及时跟踪变形又不产生极大计算代价的构形更新方式。Léger等[5]发展了一种介于TL法和UL法之间的构形更新方法，即在每个载荷步迭代平衡后将此构形作为新的参考构形，这种方法比较适用于形函数复杂、更新构形代价较大的无网格法。

由于无网格形函数的丰富性，Galerkin弱形式的准确积分要求较多的区域积分点，严重降低了计算效率。无网格领域已发展了一些高效积分方法，如Wang等[6]的子域积分、Beissel等[7]的节点积分和Duan等[8]的稳定应力点积分等。其中,Chen等[9]发展的基于应变光顺的稳定相容节点积分SCNI(Stabilized Conforming Nodal Integration)方法极具吸引力，其突出优点是不引入任何人工参数，且能精确通过线性分片试验。该方法已成功应用于几何非线性分析[10,11]，在高度不规则计算网格下仍展现出良好的计算稳定性和效率。Wang等[12]进一步将该方法拓展到板单元的大变形问题，成功克服了剪切自锁。

Puso等[13]发现SCNI仍然可能导致边界附近锯齿形振荡模式的出现。Duan等[14]也指出，即使对于二次无网格近似，SCNI也只能通过线性分片试验，而不能通过二次分片试验。本质上，SCNI是一点积分方案，只能反映出常数应变场。对于应变分布可能较为复杂的非线性问题，高阶方法更能够精确地再现变形过程，避免体积自锁。Ortiz等[15]指出，在一些大应变算例中低阶方法鲁棒性较差，对这一类问题发展高效的高阶方法是必要的。Duan等[14]针对线弹性小变形问题发展了一个三点积分方案，积分点上的形函数导数由其与形函数之间散度定理的离散形式计算。该方法可精确通过二次分片试验，因而称之为二阶一致三点积分方法QC3(Quadratically Consistent 3-point integration method)。相应的，SCNI可称为线性一致一点积分方法LC1(Linearly Consistent 1-point integration method)。目前，QC3积分方案已成功应用于不可压缩固体[15]、断裂相场[16]和斯托克斯流[17]等问题，但这些研究仍主要集中在线性分析方面。

本文把QC3积分方案拓展到几何非线性分析，并进一步引入Léger等[5]的更新构形方法，发展能够高效分析大变形问题的高阶无网格法，并通过数值结果考察和验证方法的计算精度与效率。

2 几何非线性分析列式

如图1所示，考虑当前构形为Ωn + 1，坐标为xn + 1，自然边界为Γn + 1，本质边界为Γun + 1，Γun + 1∪Γtn + 1=Γn + 1，Γun + 1∩Γtn + 1= ∅。与标准的TL和UL方法不同，本文选取第n个载荷步迭代平衡后的构形Ωn作为参考构形，该构形上的各物理量均标注下标n，如图1的Γtn和Γun。相应地，初始构形Ω0的各物理量均标注下标0。图1的Fn和fn + 1分别表示Ωn相对于Ω0以及Ωn + 1相对于Ωn的变形梯度。

当前构形下，平衡方程及边界条件为

(1)

(2)

σi jnj=tn + 1ionΓtn + 1

(3)

(4)

式中左端为内力虚功Wint，右端为外力虚功Wext。采用本文选取的参考构形Ωn，式(4)可表示为

(5)

式中bn和tn为定义在参考构形下的体力和面力载荷，Sn和En分别为

(6)

(7)

图1 计算构形

式中Jn= |Fn|，I为二阶单位张量，S和E分别为参考初始构形的第二Piola-Kirchhoff应力(PK2应力)和格林应变。显然，Sn和En分别为前推到参考构形Ωn的PK2应力和格林应变[5]。

采用节点的无网格形函数建立位移近似u=NIuI，并代入式(5)，则该式左端可表示为

(8)

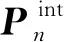
(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

式中m为节点数目，un=xn + 1-xn为参考构形到当前构形的位移增量。须着重指出的是，本文方法采用Ωn作为计算参考构形，因而式(12，14，16)的空间导数均为对xn的导数，这是与参考初始构形的传统TL法以及参考相邻构形的传统UL法的核心区别。

非线性方程的求解采用牛顿-拉普森迭代算法，计算流程简述如下。

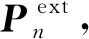
(17)

(3) 建立切线刚度阵K，并通过罚函数法施加本质边界条件求解增量平衡方程

(18)

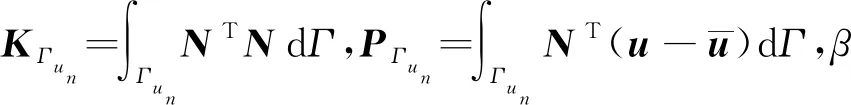
(19)

3 二阶一致三点积分格式

由以上列式可以看到，刚度阵的建立需要计算形函数导数的区域积分。由于无网格形函数是非多项式的有理函数，精确计算该区域积分需要较多的积分点，故计算效率下降。针对该问题，本文引入Duan等[14]针对线弹性小变形问题发展的三点积分格式QC3来减少积分点数目。

如图2所示，QC3方法采用背景三角形单元进行积分计算，每个单元仅使用三个积分点(五角星)，边界积分在每条边上使用两个一维高斯点(三角形)。QC3方法的核心思想是导数修正，即积分点上形函数的空间导数不采用标准形式，而是由散度定理(20)确定

(20)

式中ΩSn为参考构形下的背景积分子域，ΓSn为其边界，q(x) =p,x(x)∪p,y(x)，p(x)为MLS形函数的基底函数向量。本文采用二次近似，即p(x) =[1xyx2xyy2]T，则q(x) = [1xy]T，因而

图2 QC3积分方法

式(20)实际上表示了三个方程，刚好可以用于确定三个积分点上形函数的空间导数。采用数值积分，式(20)的离散形式为

(21)

4 数值算例

采用三个算例考察和验证本文发展的无网格方法处理几何非线性问题的有效性。作为对比，对有限元(线性三节点三角形单元，标识为FEM)、LC1以及积分点上直接使用标准导数(而非修正导数)的无网格法(标识为ST16，即每个背景三角形单元使用16个积分点)也进行了程序实现。

4.1 浅拱

如图3所示，两端固支弧形浅拱在顶部中心点A处受向下的集中载荷作用[10]。浅拱中性轴半径为100 mm，拱厚为2 mm，弧对应圆心角为 28.06°，杨氏模量E=4.8×103N/mm2，泊松比υ=0.0。无网格离散采用105个节点，分20个加载步，每步载荷为1 N，各种方法得到的A点处的载荷-位移响应如图4所示。可以看出，本文的QC3方法以及ST16方法的结果与解析解吻合良好，但是FEM和LC1方法的计算结果明显偏离了解析解。应说明的是，FEM的结果通过加密网格和改变构形更新方式(如采用UL法)可以得到显著改善。

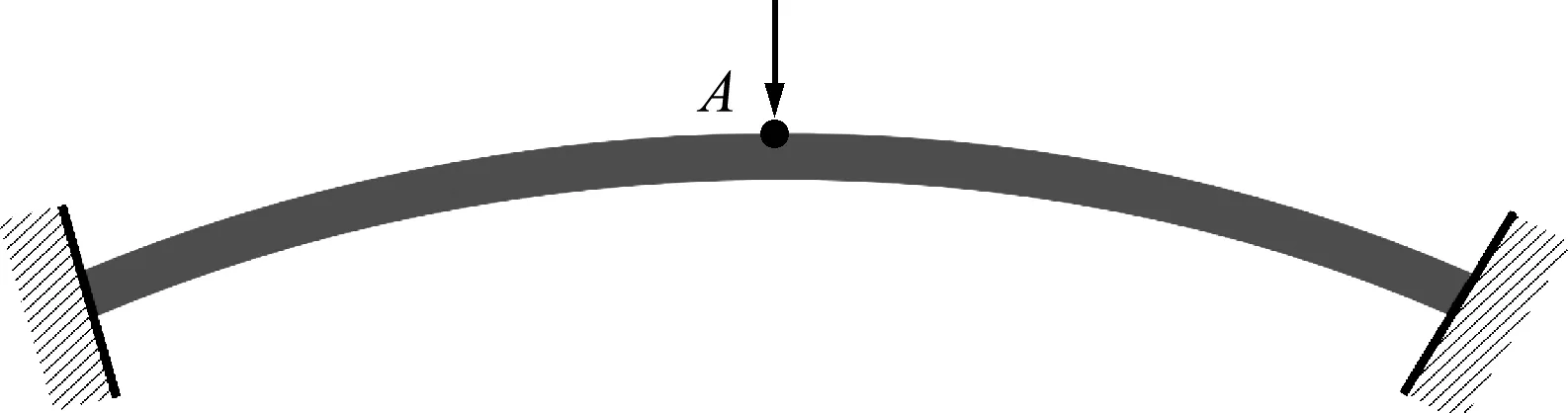
图3 受集中载荷的浅拱

图4 浅拱A点处的载荷-位移响应

QC3与ST16的计算精度相当，但QC3更为高效，表1比较了三种无网格方法在四种计算节点配置下消耗的CPU时间。显然，QC3的计算时间大约仅为ST16的1/4。

4.2 悬臂梁

如图5所示，悬臂梁一端固支，另一端部中心A处受向上的集中载荷作用[10]，梁长为20 mm，厚度为1 mm，杨氏模量E=4.8×103N/mm2，泊松比υ=0.0。采用405个节点离散，分100个加载步加载，每步载荷为0.1 N，QC3方法得到的变形过程如图6所示，载荷-位移响应的比较如图7所示。QC3和ST16的结果与解析解吻合，LC1的精度相对较差，FEM则明显偏离解析解。

图8比较了各方法得到的应力场。FEM和LC1的应力场均出现了明显的虚假数值振荡。本文QC3方法使用的积分点明显少于ST16，但两种方法得到了类似的光滑无振荡的应力场。

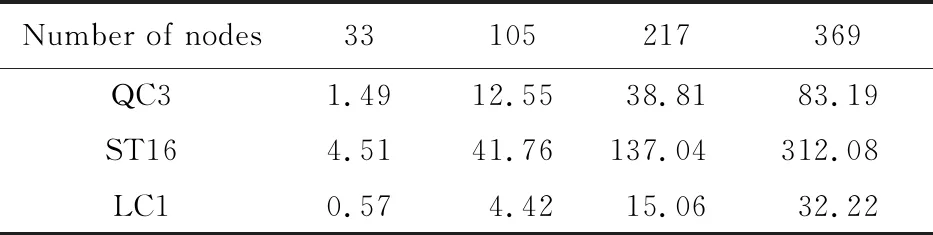
表1 浅拱算例的CPU时间比较

图5 受集中载荷的悬臂梁

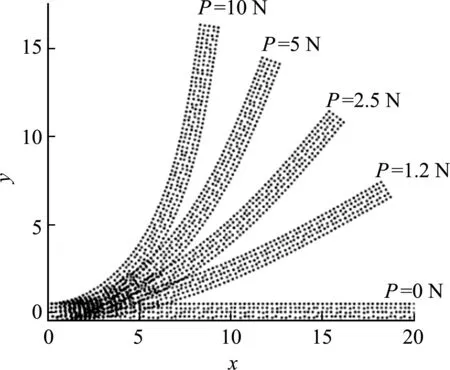
图6 QC3方法得到的不同载荷下变形后的悬臂梁

4.3 轴承座

如图9所示，轴承座尺寸为10 cm×10 cm，大孔位于正中心，四角小孔对称分布，h=1 cm，r=0.5 cm，R=4.5 cm。杨氏模量E=7.9×104N/cm2，泊松比υ=0.33。轴承座的上下表面分别施加向下和向上的不随构形变化的均匀面载荷。无网格计算采用了3830个节点,如图9所示，分50个加载步，前25步每步加载2 N直至达到极值载荷50 N，后25步每步卸载2 N直至完全卸载。

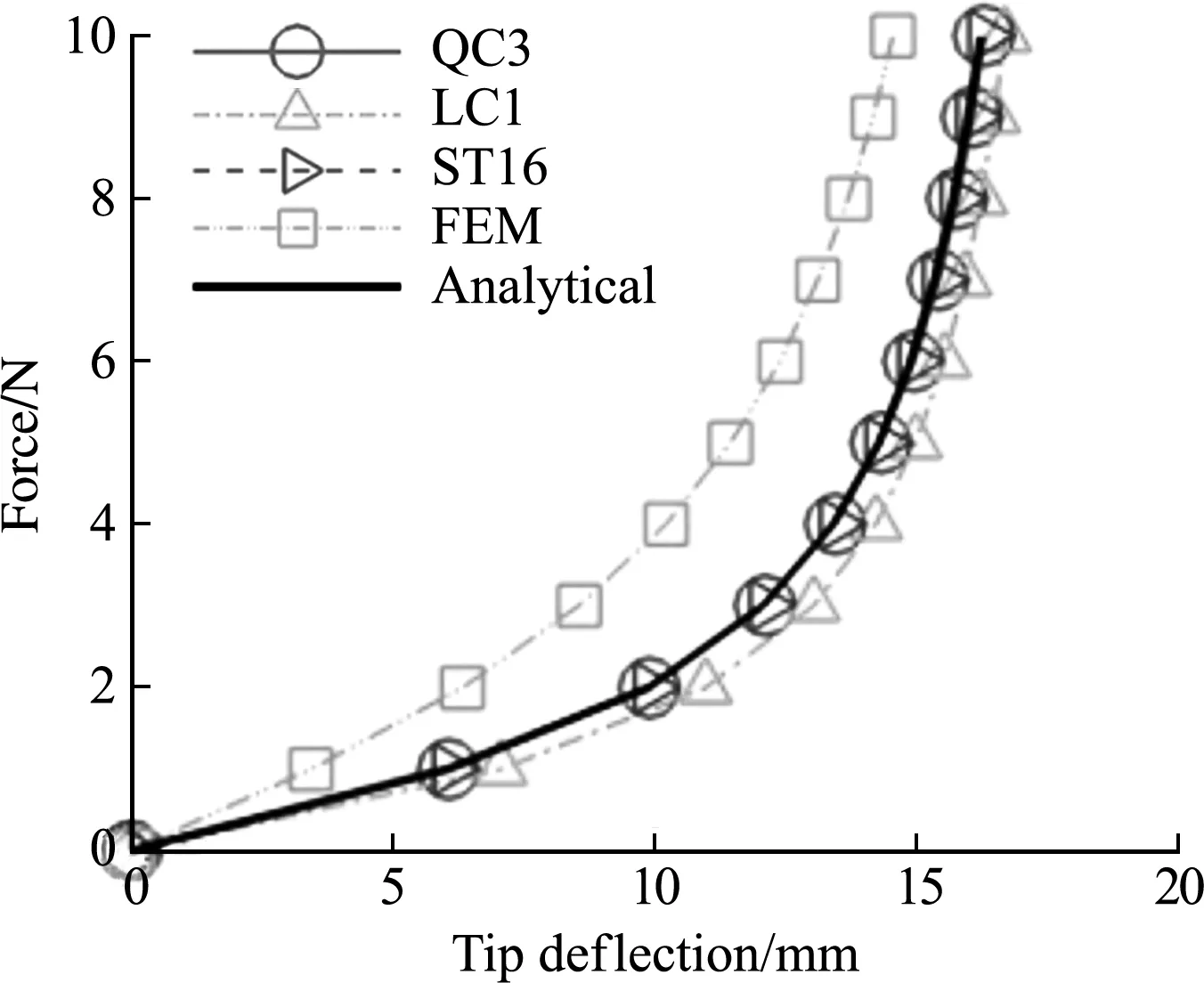
图7 悬臂梁A点处的载荷-位移响应

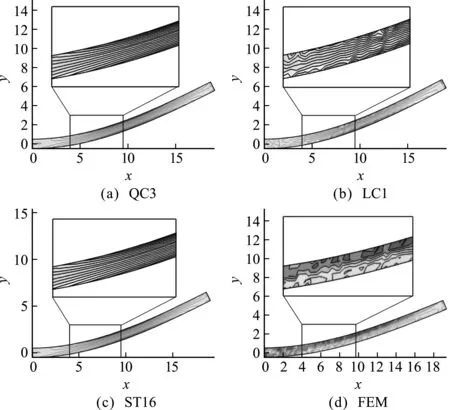
图8 悬臂梁的σx x场

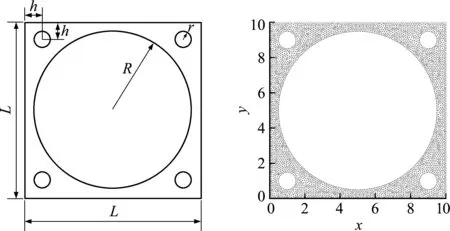
图9 轴承座的几何模型和计算节点

图10为P=20 N时轴承座的y向正应力场。以Abaqus结果为参照，QC3得到的应力极值较为准确，而LC1明显偏离参考解。图11展示了QC3方法得到的轴承座加卸载的变形过程。在完全卸载后轴承座与初始构形吻合良好，无虚假残余变形，这进一步验证了本方法计算复杂结构大变形的能力。

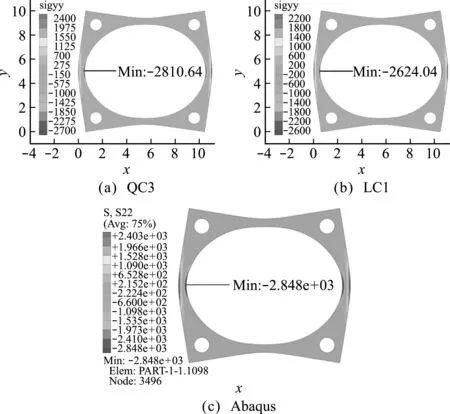
图10 轴承座的σy y场

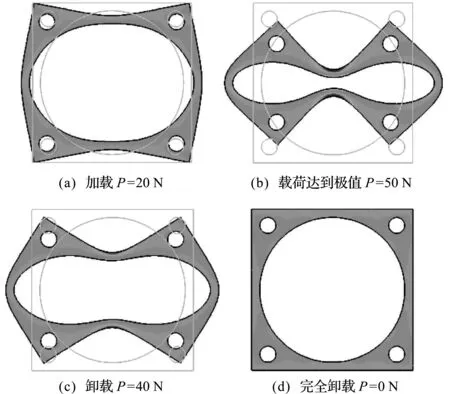
图11 QC3得到的轴承座的变形过程

5 结 论

本文将QC3方法拓展到了几何非线性分析，并采用上一载荷步的收敛构形作为计算参考构形，针对超弹性材料建立了大变形分析的高阶无网格法。与标准的高阶无网格法(ST16)相比，本文方法大幅度减少了积分点数目，节省了大量的计算时间。与一点积分的高阶无网格法(LC1)相比，本文方法具有高得多的计算精度。因此，本文方法有效提高了高阶无网格法几何非线性分析的计算效率，是超弹性材料大变形问题值得考虑的计算方案。