基于概率密度演化理论的LRB隔震支座时变可靠度研究

王思文， 王宪杰， 胡 彪， 李承玥， 张 帆

(云南大学 建筑与规划学院，昆明 650500)

1 引 言

结构参数随机性对工程的影响一直伴随着工程设计和建造等全过程。经过大量研究工作的持续投入，取得了系列成果[1]。90年代末到新世纪初，我国学者发展了随机系统分析理论，为随机结构可靠度的求解提供了新的途径[2]。李杰等[3]提出随机结构动力响应的概率密度演化方法PDEM(Probability Density Evolution Method)，可精确高效地获得随机结构概率反应信息。梅真等[4]将PDEM方法结果与统计结果对比，证明了该方法的高效与准确性。范文亮等[5]基于PDEM方法推导了结构承载力裕度的概率密度演化方程，研究了钢筋混凝土框架结构的体系可靠度等。诸多研究已证明概率密度演化理论这一新方法的应用范围正逐渐普及开来。

实际工程中，隔震支座长期与外界环境接触，不可避免会老化。同时，在生产支座的过程中，因材料和尺寸存在不确定因素，致使支座力学参数具有一定随机性。对此，已有学者进行了相应探究，Kato等[6]发现长期服役后的隔震支座水平刚度显著增大;Oh等[7]证明加速老化后支座的剪切刚度、能量吸收和等效阻尼系数受到了影响；薛斌等[8]〗指出橡胶剪切模量和铅芯屈服强度的变异会影响等效水平刚度的不确定性。因此，对支座老化衰退以及参数的不确定性应予以重视。

等效水平刚度是影响建筑隔震效果的一个重要力学指标，其值越小，隔震效果越好；相反，其值越大，致使上部结构地震响应加大[9]。在役支座刚度减小或增加过大都不利于隔震建筑的安全性，因此，对隔震支座可靠度的研究具有重要的工程意义。

现有关于支座力学性能的分析大多是确定性的分析，并没有考虑支座材料性能的衰退；或仅考虑材料衰退而忽视了材料衰退与参数不确定性的耦合影响。在前人对LRB支座试验研究的基础之上，本文引入橡胶材料的随机性、时变性及铅芯弹模的随机性，得出橡胶和铅芯的随机时变本构模型，构建LRB支座随机时变有限元模型，探究支座等效水平刚度的退化趋势。最后，基于极值分布事件概率密度演化理论得出不同老化时间下支座等效水平刚度的概率密度演化曲线和衰退规律，求解不同老化年限下LRB支座的时变可靠度，为隔震工程设计和既有隔震支座的更换和维护提供一定的理论支持。

2 LRB支座随机时变本构关系

2.1 Mooney-Rivlin超弹性本构模型

LRB支座中的硫化橡胶材料有着体积不可压缩的特点，且具有优良的弹性和恢复性。和金属等材料初始时刻即展现出线弹性本构关系不同，橡胶本构具有非线性的特点，不能简单用弹性模量来描述，其本构可以由式(1，2)表示[10]。

(1)

(2)

式中W为应变能函数，N为阶次，Ck l为材料常数，k和l为所取级数最低次幂第一项对应的指数，一般取0或1，Dk为不可压缩系数，J为弹性体积比，I1,I2和I3分别为第1,2，3应变不变量，λ1,λ2，λ3分别为第1,2，3拉伸比。

当N= 1和I3= 1并取最低次幂时，式(1)可用傅里叶级数式表示，即得式(3)的Mooney-Rivlin本构模型。对橡胶而言，材料常数C10和C01可根据式(4～6)[11]由橡胶硬度间接换算得出。

(3)

lgE0= 0.0238Hr-0.9905

(4)

E0= 6(C10+C01)，C01= 0.25C10

(5，6)

式中Hr为橡胶硬度，E0为橡胶弹性模量，D1为k取1时对应的不可压缩系数。

2.2 橡胶材料性能的衰变

LRB隔震支座由钢材、铅芯和橡胶组成。其中，钢板和铅芯的性质较为稳定，力学性质改变缓慢，而橡胶材料随着使用时间的增加，分子层面的化学性质发生改变。橡胶老化是一个缓慢的过程，为便于试验研究，文献[12]提出化学反应速度论，并指出实际环境中的材料老化时间与加速老化时间存在换算关系。马玉宏等[13]在其理论基础上，进一步归纳出式(7)。在单纯考虑热老化因素时，对支座橡胶材料进行了2160 h(等同于20 ℃环境使用180年，详见文献[13]图24)超长周期的加速老化试验，部分试验时间与自然老化时间的换算关系及数据列入表1和如图1所示。

表1 试验时间与对应自然环境20 ℃的老化时间

(7)

式中Ea为反应活化能，R为气体常数，Treal为自然环境中的绝对温度，Ttest为热氧加速老化试验绝对温度，treal为自然老化时间，ttest为试验老化时间。

因我国建筑设计基准期较长，一般在50年以上，房屋产权为70年，具有较长的使用年限。为使研究范围覆盖大多数房屋的寿命周期，图1中0～84年数据点是下文的数据基础。可以看出，橡胶的老化并不是线性关系，在0～16年增加速度较快；随后因试样外层橡胶老化起了一定隔绝作用，减慢了内部橡胶的老化；16～36年出现了平台期，此时橡胶硬度较稳定；在36～84年继续上升，与前16年相比增加速度较缓。为了进行针对性分析，选取0年，4年，12年，16年，24年，40年，60年，72年和84年的老化时间作为目标时刻。

2.3 支座等效水平刚度不确定性

目前，已有大部分研究采用确定性的力学指标来衡量隔震支座的力学性能。实际上，支座在制造过程中不可避免地存在诸多随机性因素，如支座的几何尺寸、材料弹模和橡胶材料常数等，最终导致支座等效水平刚度的不确定性。本文选定橡胶材料常数和铅芯弹模Eq作为LRB支座材料层面的时变和随机性因素，并假设其服从标准正态分布。根据贵州轮胎股份有限公司对橡胶材料样品的基础试验数据，近似拟合出式(8)所示橡胶材料常数变异系数Cv的时变关系。变异系数和材料常数概率取值列入表2，Eq均值取16000，变异系数取0.02。式(9，10)即为橡胶和铅芯材料的随机本构关系模型表达式。

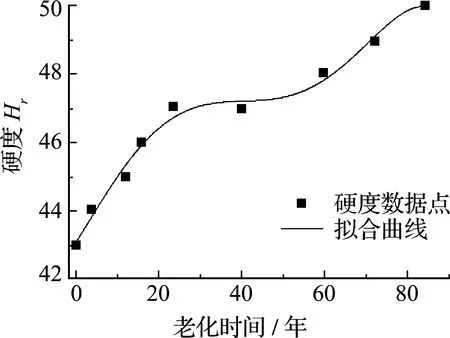
图1 加速热老化试验数据[13]

表2 材料常数概率信息取值Tab.2 Probability information of material constant

Cv(t) = 0.000363e0.06201 t+0.04164e0.01213 t

(8)

W(μ1,σ1) =C10(μ1,σ1)(I1- 3)+

(9)

(10)

规范《建筑隔震橡胶支座JG/T118-2018》[14]规定隔震支座的等效水平刚度计算式为

Kh= (Q+-Q-)/(U+-U-)

(11)

式中Kh为等效水平刚度，U+和U-为支座的最大和最小位移，Q+和Q-为最大和最小位移对应的最大和最小剪力。

LRB支座等效水平刚度的理论值计算式为[15]

(12，13)

(14，15)

3 基于概率密度演化理论极值分布的可靠度求解

PDEM理论是一种新兴的随机性理论方法，高效而准确，为求解复杂随机问题提供了一种新的途径。结构的可靠度可定义为

R(t) = Pr{X(τ) ∈Ωs, 0≤τ≤t}

(16)

式中R(t)为结构可靠度函数,X(τ)为致使结构失效的物理因素,Ωs为安全域,t为参考时间。

根据不同的判别标准，PDEM方法求解可靠度问题可分为单侧吸壁问题和双侧吸壁问题等[16]。规范[14]指出，老化后支座等效水平刚度的变化量应在+20%之内，存在一侧限值，故适合采用单侧吸壁准则式(17)来定义其变化区间限值。

R(t) = Pr{X(τ) ≤b, 0≤τ≤t}

(17)

根据PDEM方法的基本思想[17],求解极值分布事件可靠度的核心是构造一个虚拟随机过程Ql(τ)，在虚拟时间τ中使目标随机变量为该过程的截口随机变量Zl(τ= 1)。以该过程为桥梁，进而求解目标随机变量的概率密度函数[18]，如式(18,19)。式(20)即为依赖于随机参数Θ定义的随机结构反应绝对值的最大值。

Zl=Ql·τ=Wl(Θ,T) ·τ

(18)

Zl=Ql(τ)|τ =1

(19)

(20)

进一步，可得到(Ql,Θ)的联合概率密度函数pQl Θ(q,θ,τ)的概率密度演化方程(21)和相对应的初值条件(22)。

(21)

pQlΘ(q,θ,τ) |τ = 0=δ(q)pΘ(θ)

(22)

式中δ(q)为Dirac函数。

求解偏微分方程(21)初值问题,联立式(21，22)即可求出pQlΘ(q,θ,τ)的数值解，再代入式(23～25)求出可靠度。

(23)

pz1(z) =pQl(q,τ)|q =z,τ =1

(24)

(25)

根据数论选点法在三维随机变量Θ的三维分布空间Ωθ中选取若干个代表点，求出等效水平刚度Kh。根据式(19)构造的虚拟随机过程如式(26)所示，则虚拟随机过程Z(τ)关于τ的导数即为式(27)。

Z(τ) =Kh(θi,j) · sin(τ· π/2)

(26)

式(26)满足Z(τ)|τ =0= 0,Z(τ)|τ =1=Kh(θi,j),当τ= 1时，Z(τ)即为真实的等效水平刚度。

4 算例分析

4.1 参数选取与有限元模型的建立

依照图2 所示的LRB支座结构形式进行有限元建模，模型的尺寸大小参照规范[14]对支座尺寸规格的规定，选取支座直径为Ф600 mm进行建模。为了便于分析，暂不考虑封板中的螺栓和支座橡胶保护层的厚度，以及外层橡胶老化后对内部橡胶的延缓效果，模型具体尺寸参数列入表3。

橡胶材料常数取值基于表2的概率信息，经由数论选点法生成；钢板选用Q235钢，钢材弹模EG= 206000 MPa，采用随动硬化本构关系[20]，应力σ1，σ2及应变ε1，ε2的取值分别为235 MPa，444 MPa及0,0.1812，泊松比μG=0.3；铅芯弹模Eq=16000 MPa；泊松比μ=0.44，屈服强度σs=10.2 MPa，采用理想弹塑性本构关系[21]。

LRB支座具有轴对称的特点，为提高收敛性和计算效率，对支座模型进行如下简化。以xOy平面为基准面，沿X轴方向切去一半，可减少一半网格数量。因支座在组装过程中的硫化工艺可使钢板层和橡胶层间产生极强的黏结力，很难产生剥离破坏，且铅芯在制作时直径会略大于中孔直径，以使铅芯和钢板-橡胶复合体紧密相连。因此，将支座的钢板、封板、橡胶层和铅芯合并为一个构件，细部构造如图2所示，模型展示如图3所示。

因橡胶体积不可压缩的性质，取D1=0。为防止模拟过程中材料进入非线性阶段发生体积自锁的现象，橡胶选用8结点线性6面体杂交单元C3D8H；钢板和铅芯采用8节点线性6面体减缩单元C3D8R。

加载方式采用正弦幅值位移加载，位移的限值为±114 mm(即使支座产生100%的剪切变形)，仅对支座上封板圆心施加位移荷载。规范[14]要求加载频率f≥0.02 Hz，取f=0.5 Hz。模型底部锁定所有自由度，剖面方向约束Y方向平动自由度，顶部释放X和Z向平动自由度，约束其他自由度。

《建筑抗震设计规范GB/50011-2010》[22]规定，各类隔震建筑支座竖向压应力应小于等于15 MPa，综合考虑课题组涉及隔震项目中柱结构轴力，取压强P=7.07 MPa。

4.2 结果分析

篇幅所限，在4.1节加载方式基础之上，仅绘制出支座经4年、16年、60年和84年老化后的滞回曲线(图4)。随着老化时间增长，滞回曲线逐渐呈现出一定的非线性关系，橡胶老化变硬后不再是最初的理想超弹性本构，支座性能产生了退化。图4反映出加载位移不变的情况下，随着老化时间增加，支座的反力同步增大，滞回曲线Y轴峰值呈上下移动的趋势，支座变刚。图5为经式(9)计算后所有目标时刻支座等效水平刚度的变化趋势。老化后支座的等效水平刚度(图5)与橡胶材料的硬度(图1)有着相似的变化规律，即随着时间推移，刚度以两次不同的速率增大直至平台期，最后以较平稳增长速率继续增大。

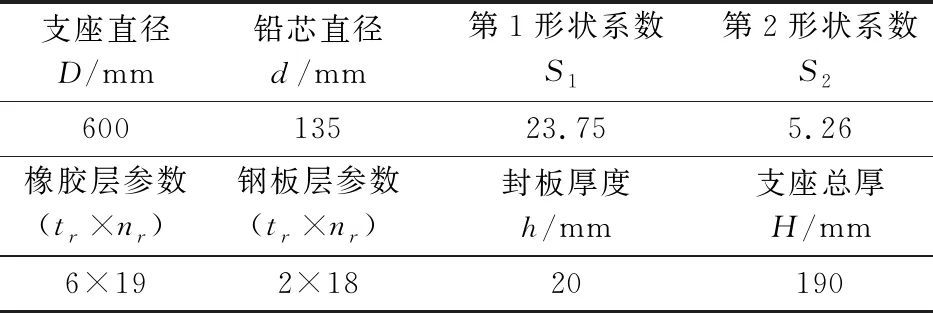
表3 LRBФ600支座几何尺寸

图3 LRB支座有限元模型

但需要指出的是，文献[23]表明当LRB支座产生小应变以下剪切变形时(γ≤150%)，有限元方法对支座刚度的模拟较好，但对等效阻尼比等其他参数的模拟存在误差；支座剪力-位移限值的模拟值与试验值较契合，而式(11)的刚度正是基于该限值求得，因此本文采用有限元方法模拟LRB支座等效刚度具有一定可行性。从图4可以看出，LRB支座滞回曲线中加载和卸载阶段的折角较尖锐，原因在于有限元模拟时没有考虑试验中加载设备与支座之间的相对滑动。

在有限元模拟完成后，取Ar=268429.5 mm2，α=0.216，σp b=10.2 MPa，代入式(12～15)，即可计算出等效水平刚度的理论值。目标时刻LRB支座等效水平刚度模拟值与理论值对比列入表4。

图4 部分老化时间滞回曲线变化

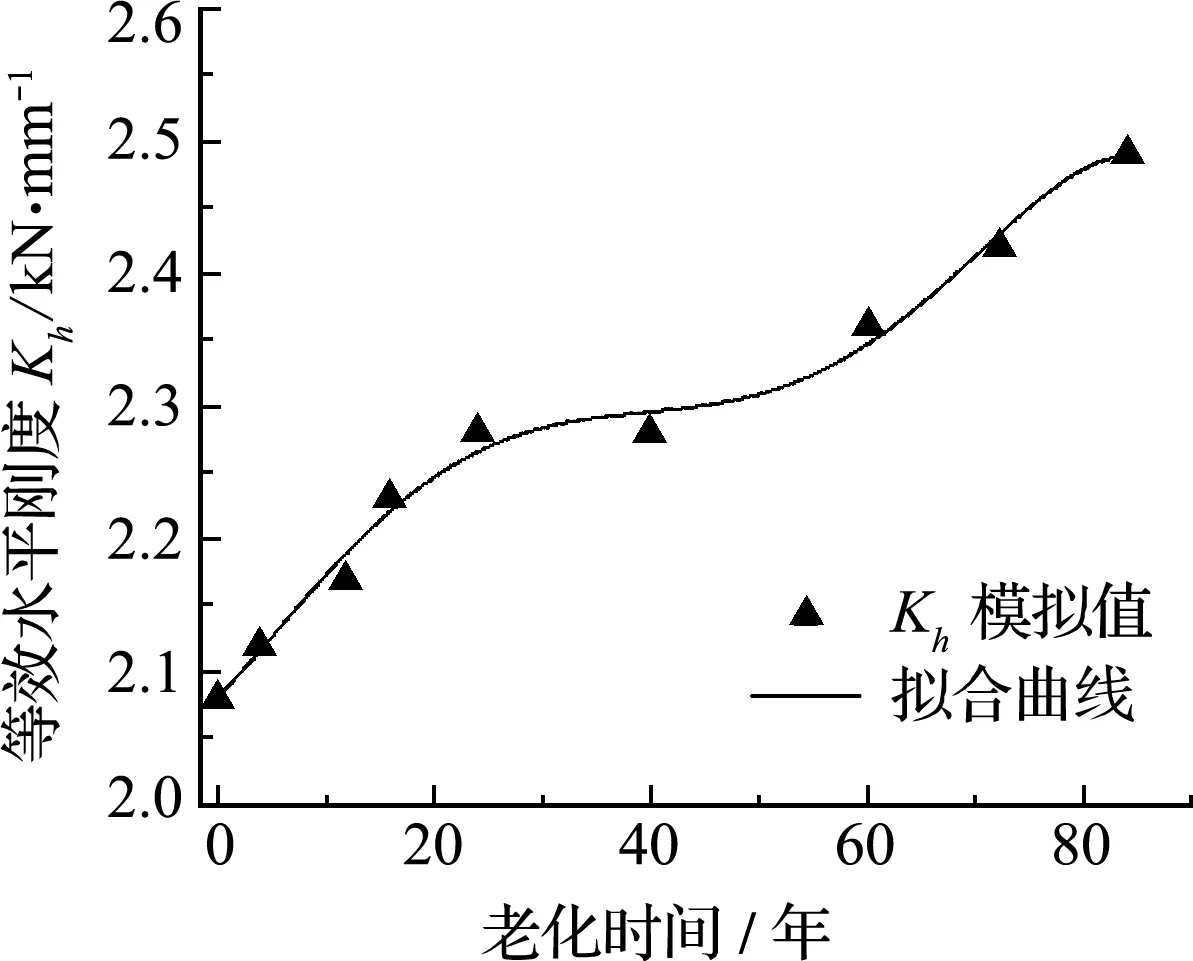
图5 等效水平刚度变化趋势

由表4可知，不同老化时间下，模拟值与理论值的误差在5%～7%之间，平均误差为6.3%，采用有限元软件能够以较小的误差对LRB支座水平力学性能进行模拟，获得精度良好的等效水平刚度结果，进一步验证了文献[23]的有限元可较好模拟支座中小应变下水平刚度的结论。采用有限差分法求出方程(21)的解,为了直观地反应等效水平刚度的演化过程，同时绘制等效水平刚度2维和3维的概率密度演化曲线(面)，如图(6)所示。

表4 不同老化时间支座等效水平刚度模拟值与理论值的对比

可以看出，随着老化时间增加，概率密度曲线呈现右移，表示LRB支座等效水平刚度产生了如图5所示的刚度退化，证明概率密度演化理论对LRB支座等效水平刚度的衰退有良好的表达。从 图6 和图7可以看出，各老化时间等效水平刚度PDF值表现出下降的趋势；老化40年之后，下降速率增加且概率密度演化曲线的轮廓逐渐趋于扁平，故老化对支座等效水平刚度离散性的影响较明显。

由式(17)单侧吸壁条件K(τ) ≤2.5,0 ≤τ≤1和式(23～25)可得表5可靠度，变化趋势如图8所示。可以看出，老化后支座可靠度呈下降趋势，在0～10年可靠度比较稳定；10～25年可靠度出现第一次下降；25～41年可靠度进入第二个稳定期，41～84年可靠度再次下降；随着老化时间增加，支座可靠度变化率逐渐增大。由此可见，在LRB支座服役时间达到20年前后，要加大检测频率；而40年后，需要检修或有条件的更换，以确保隔震结构维持设防的抗震能力。

图6 目标时刻概率密度曲线(面)的演变过程

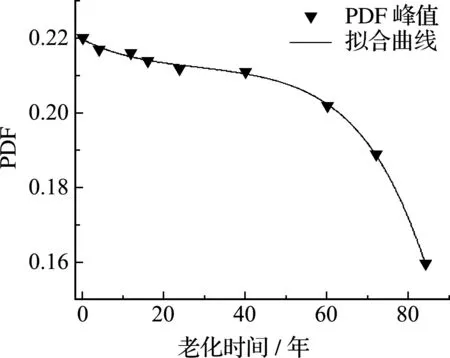
图7 PDF值随时间变化情况

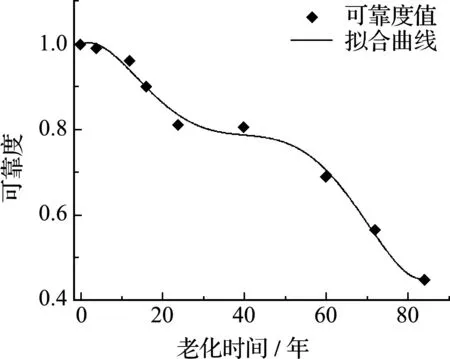
图8 可靠度随老化时间增加的变化趋势

表5 不同老化时间LRB支座可靠度Tab.5 LRB bearing reliability at different aging times

5 结 论

本文对LRBФ600支座算例等效水平刚度的衰退趋势进行了分析，并将有限元模拟值与理论计算值进行对比，进一步验证了有限元方法模拟支座水平刚度的准确性和可靠性。基于概率密度演化理论求出目标时刻支座等效水平刚度与可靠度，最后得到如下结论。

(1) 概率密度演化理论可准确有效地捕捉目标时刻LRB支座时变本构关系的概率信息，得到等效水平刚度随老化时间的演化规律。支座在老化后，等效水平刚度也随之增加。

(2) LRB支座的老化是一个非线性的过程。老化后支座外围橡胶老化变硬延缓了内部橡胶的老化，存在两个平台期，此时可靠度比较稳定。在平台期外的两个时间段，可靠度下降较明显。

(3) 在橡胶材料常数和铅芯弹模时变变异系数确定的情况下，老化后各目标时刻概率密度演化曲线的峰值明显降低，概率密度曲线的形状逐渐扁平，老化增大了LRB支座等效水平刚度离散性。

本文的研究为在役LRB隔震支座的维护和更换提供了一定的理论支持，但不同支座种类橡胶是否均可视为体积不可压缩材料目前尚不明确，相关的研究工作，课题组正陆续开展。