直径限定可靠性计算的冗余边的检测算法

熊祥军， 邵方明， 张祖渊， 管建民

（1. 华东理工大学理学院，上海 200237；2. 长春财经学院数学系，长春 130122）

经典的二终端网络可靠性是指源节点s 和终端节点t 之间存在至少一个操作路径的概率，但是不考虑对st-路长度的限制。通过限制所有st-路的长度不超过给定正整数D，Petingi 等[1]最初将直径限制引入网络可靠性（DCR）。Cancela 等[2]研究了通信网络的直径限制可靠性模型，并提出了一种多项式时间算法，用于检测和删除冗余边，以计算具有直径限制的简单无向图的二终端可靠性。在DCR 模型中，检测冗余边的必要条件尚未得到解决。此外，文献[3]中做了进一步的工作。文献[4]中将s，K-直径定义为源节点s 与K 中任意节点之间的最大距离，使用控制以提出一种简单的方法来计算s，K-直径不大于给定值D 时的可靠性。然而，检测冗余边的必要条件仍然是一个悬而未决的问题。

计算二终端可靠性的问题是NP-难的问题。因子分解算法[5]是评估可靠性的有效方法。通过使用这种算法，Cancela 等[2]研究了文献[6]中网络的结果，这些结果也用于本文。

多项式时间拓扑归约在直径限制可靠性的计算中起重要作用，因为许多冗余边能够被删除并且可靠性保持不变。然而，以往对冗余边的研究并不全面。检测冗余边的必要条件是所谓的开放问题。在本文中，我们基于文献[7]定义路径长度的新度量方法，将 st-路径分类为实际路径（RP），伪路径（PP），组合路径（CP），包含特定边的最短 st-路径（SPE）并明确指出通过测量PP、RP 和CP 可以得出SPE 的长度。此外，我们提出了一种检测隐藏冗余边的算法，该算法的复杂度是多项式的(O(n4))。

1 系统模型和冗余边问题

1.1 系统模型

通信网络可以通过概率图G（V，E）在数学上建模，其中V 是节点集合，E 是边的集合。每个节点v∈V 是完全可靠的，而每个边e∈E 独立地失效并且与操作概率pe（失效概率qe=1-pe）相关联。图1 示出了具有节点集 V={s，a，b，c，d，t}的通信网络 G，其中源节点和终端节点分别是 s、t，边集 E={e1，e2，...，e11}。

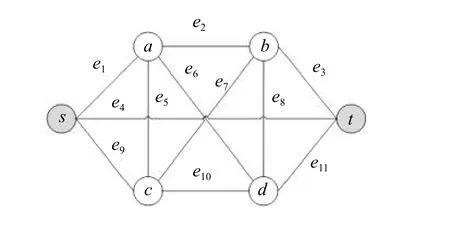
图 1 通讯网络G (V, E)Fig. 1 Communication network G (V, E)

定义 1[1]：由 Rst(G)表示的st 可靠性是指源点s 和汇点t 之间至少存在一条连通路径的概率。

文献[5]提出了因子分解算法来计算st 可靠性，这被认为是NP-难问题。可靠性计算的因子定理：

1.2 直径限制二终端可靠性

定义3：直径限制下的二终端可靠性是指至少存在一条长度小于D 的st 路径，记为Rst(G, D)。

通过因子分解定理计算：

值得注意的是，收缩边e 得到图 G *e 的过程可能会使原来经过边e 的长度为D+1 的路的长度减少到D，从而导致计算Rst( G *e , D)时将多余的路径计算在内的情况。因此，我们设定固定边e 的状态为1 并保留边e 在图中的位置不变。

1.3 冗余边问题

Petingi 等[3]提出检测冗余边的充分条件。

命题1：e=uv 是存在于图G 某个st-路上的边。如果 dG-e(s, u)+dG-e(v, t)≥D 和 dG-e(s, v)+dG-e(u, t)≥D，则边e 是冗余边。

与[2]中结果相比，命题1 可以被认为是路径长度的新的度量方法，但它仍然不能完全找到冗余边。比如在图2 中，给定D=5，冗余边e=bc。从命题1，dG-e(s, b)+dG-e(c, t)=4＜D 并 且 dG-e(s, c)+dG-e(b, t)=4＜D可知e=bc 并非冗余边。

造成这种现象的原因是该度量仅考虑路径长度，但忽略了从源点s 到点u 和点v 到汇点t（从s 到v 和u 到t）的路径的具体信息以及路径的组合是否包含给定边uv。因此dG-e(s, u)+dG-e(v, t) 和 dG-e(s, v)+dG-e(u, t)的度量仍然需要进一步改进。

图 2 无法用命题1 判断冗余边的拓扑结构Fig. 2 Topology structure with irrelevant edges not identified by Proposition 1

2 检测冗余边的分析和算法

2.1 冗余边的分析

设定 P1, P2, …, Pm都为包含边 e 的 st-路，

定理 1：如果 min1≤i≤m|Pi|＞D，则 e 为不相关边。

显 而 易 见 ，min1≤i≤m|Pi|＞D 意 味 着 所 有 包 含 边e 的st-路径的长度大于D，因此边e 必然为冗余边。反之，如果边e 为冗余边，则所有包含边e 的st-路径的长度大于 D，例如，min1≤i≤m|Pi|＞D。

为了更有效地检测冗余边，我们考虑包含边e（SPE）的最短 st-路径[3]。如果找到 SPE，则肯定会完全检测到所有冗余边。但是，Petingi 等[3]证明找到SPE 的问题是NP-难的。我们希望在多项式时间内找到接近SPE 长度的值，并使用该值与D 进行比较以确定冗余边。

对于节点 x，y，Px,y表示从 x 到 y 的最短路径之一。对于边 e=uv，我们称 Ps,u∪(u, v)∪Pv,t和 Ps,v∪(v, u)∪Pu,t分别为 u，v-path 和 v，u-path。为方便起见，我们只讨论如何处理 u，v-paths 并对 v，u-paths 进行相同的操作。

推论1：包含边uv 的最短路径然必然是包含u，v-paths 和 v，u-paths 中最短的路径。

图 3 RP 和 CP 的示例Fig. 3 An example for RP and CP

在图4 中，可以看到每个步骤都对上一步进行进一步度量。事实上，检测所有冗余边是基于SPE 的值，而不是SPE 本身。在我们的算法设计中，我们并没有尝试寻找SPE，而是使用SPE 的长度或其近似值。

以上分析侧重于有向边 (u, v)。对于边（v，u），操作是相同的。不可否认，存在最短路径不唯一的情况，实际上这并不会影响冗余边的检测，因为PP，RP 和CP 重复检查两个节点之间的最短路径。更明确地，如果通过删除Ck损坏了最短路径之一，则度量将测量其他最短路径。

表 1 路径长度的度量标准Table 1 Metrics of path lengths

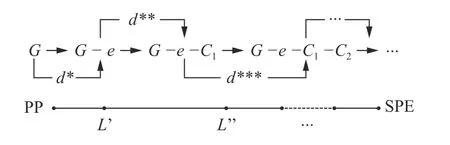
图 4 从 PP 到 SPE 的长度Fig. 4 Length matric from PP to SPE

2.2 检测冗余边的算法

将归约过程整合到因子分解定理中，我们得到可靠性计算程序（RCP）：

输入：G (V, E)，源点 s，汇点 t，p，直径限制 D

输出：Rst(G, D)

步1：如果G 直径小于或等于D，执行步3；否则执行步2；

步2：执行NRP 以获得新网络G0；

步3：在G0中随机选择边e；

步4：递归计算Rst(G*e, D)；

步5：递归计算Rst(G-e, D)；

步 6：Rst(G, D)=pRst(G*e, D)+qRst(G-e, D)。

复杂性分析：文献 [8]表明，对于 D=2，Rst(G,D)可以在多项式时间内确定，并且计算D, D≥3 的固定值的Rst(G, D)是NP-难问题。

3 实例分析

在本节中，我们将说明检测冗余边的不同拓扑，并显示Petingi 算法与我们算法之间的比较。图5 说明了 4 个图：5（a）循环 C [6]; 5（b）Arpanet [6]; 5（c）欧洲光网络[6]; 5（d）加齐大学网络[6]。该算法被编码为 MATLAB 程序，并在 PC（Intel Core i5; 2 450 M;2.5 GHz CPU）上实现。

表2 显示了所提算法和Petingi 算法[2]之间冗余边数和CPU 时间的比较，其中，*IE1, T1分别为本文算法的冗余边数量和 CPU 时间；IE2, T2分别为Petingi 算法冗余边数量和 CPU 时间[2]；T：未减少计算可靠性的CPU 时间。当D=3 时，在图5（a）中检测到两个冗余边，并且CPU 时间节省0.007 6 s。当D=5 时，我们在图 5（b）中找到两个冗余边，CPU 时间节省4.439 s。在许多例中，通过使用我们的算法可以完全找到冗余边。通常，冗余边的数量与直径限制 D 密切相关。例如，在图 5（c）和表 2 中，D 越小，冗余边越多，CPU 时间越少。当D＜7 时，我们的算法检测到的冗余边比Petingi 算法更多。然而，当D=7 时，Petingi 算法的冗余边数与我们的相同，并且CPU 时间相近。

表3 显示了我们的算法和Petingi 算法之间冗余边数和CPU 时间的比较，其中，IE1, T1分别为本文算 法 的 冗 余 边 数 量 和 CPU 时 间；IE2，T2分 别 为Petingi 算法冗余边数量和CPU 时间[2]。总的来讲，Petingi 的算法和我们的算法都能有效地检测不相关的边缘。如果D 的值太小，则Peting 的算法更快，因为相关边的数量很小。例如，由于网络没有长度为3,4 和5 的路径，因此在D=2,3 的网络中有20 个冗余边（只有边s1 和1t 是相关的）。但是，我们的算法的优点在D=4, 5, 6, 7 和8 时通过事实凸显出来，结果见图6。原因是我们的算法能够在检测冗余边时清楚地找到PP，从而找到最内部冗余边。因此，计算可靠性的相应CPU 时间进一步减少。最后，从s 到t 的最大距离是9，此时，我们的算法和Petingi 算法的CPU 时间接近。

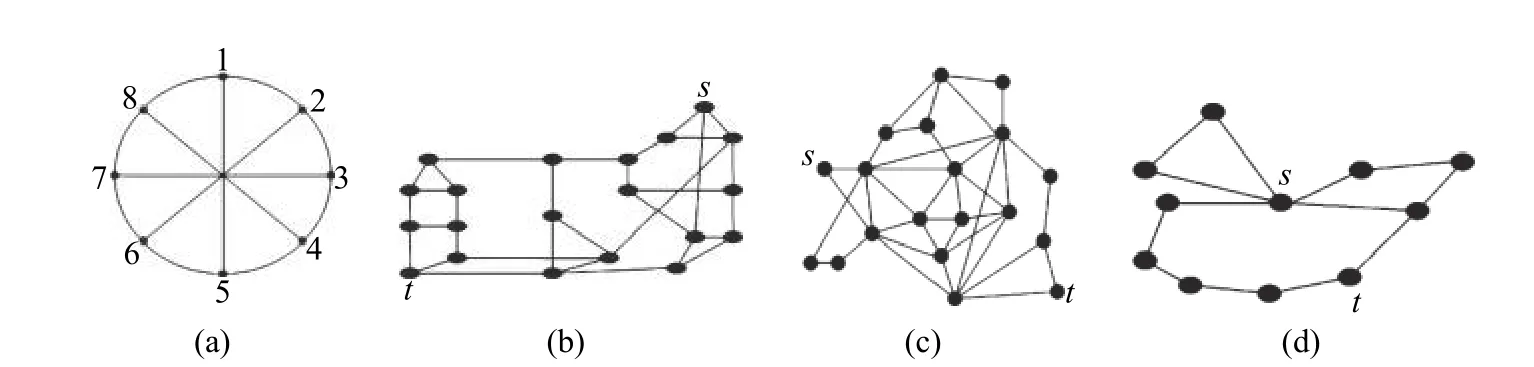
图 5 拓扑示意图Fig. 5 Illustration of four topologies

表 2 数值结果（p=0.9）Table 2 Numerical results with p = 0.9

表 3 冗余边的检测及可靠性计算时间（p=0.9）Table 3 Detection of irrelevant edges and computation of reliability for p = 0.9

图 6 比较不同D 值的示意图Fig. 6 An illustration for comparison of different values of D

4 结 论

我们在检测直径限制可靠性的冗余边方面做了进一步的工作。提出的一些路径长度度量来改进检测隐藏的冗余边的方法。实例分析结果表明所提出的算法能够在多项式时间(O(n4))中识别更多冗余边。