刀片式多排密集圆孔气体冲击射流冷却的实验研究
邢改兰, 赖焕新, 刘华飞
(1. 华东理工大学机械与动力工程学院, 上海 200237;2. 宝钢股份有限公司研究院,上海 201900)
工业过程中经常遇到需要快速冷却高温物体或者在有限空间内持续冷却运动高温板带的场合,如高负荷微电子元件在狭小空间内需快速排出电流产生的焦耳热以维持正常工作温度[1];带材连续生产线上需要高且均匀的热流密度以对运动带材实施气体淬火,保证马氏体组织转变均匀[2-3];航空发动机涡轮叶片内部通道通过实施强制冷却以使其在高温环境下正常运转[4-6]。从传热的角度讲,上述冷却过程都需要比较大的换热系数,气体冲击射流冷却可以适应这种需求。冲击冷却通常是气体从圆孔或狭缝型喷嘴喷射到固体表面,由于其流动行程短,边界层薄,因而换热系数比常规的管内流动换热系数高出几倍直至一个数量级。对于给定的换热系数,采用冲击换热原理设计的装置比常规装置在尺寸上通常小 1~2 个数量级[7-9]。
在圆孔气体射流换热方面,前人多是采用实验方法研究冲击换热系数,获得传热准数方程。Gardon 等[10-11]揭示了冲击射流局部换热系数非单调性变化是由于湍流度变化的缘故,并以喷嘴间距Xn为定性尺寸定义努谢尔数(Nu),引入到达速度定义雷诺数(Re),获得的准数方程在目前的工业设计中被广泛采用。Martin[12]以Krotzsch[13]的传质实验数据为基础,通过传热传质类比,总结出适用性更广的单股圆孔射流和圆孔阵列射流准数方程。Martin 公式以喷嘴直径D 为定性尺寸,综合考虑了各种几何因素(如喷射高度、开孔率)、喷气速度与介质种类等的影响,并讨论了喷射系统的最佳结构参数问题。Kuntikana[14]和Viskanta[15]通过实验分析了气体冲击射流和火焰冲击射流的传热过程,研究结果均针对特殊的几何结构。Zuckerman[16]列举了多位研究者的单孔和多排圆孔射流的传热准数方程,Meola[17]探讨了对多排圆孔射流建立新的通用传热关联式的方式。
通常冲击射流的传热准数影响因素可归因于流体特性和结构参数,流体特性主要指雷诺数和普朗特数(Pr),结构参数通常指量纲为一喷射高度(H/D)和量纲为一喷嘴间距(Xn/D)或者开孔率(Af)。但是对比已有文献研究可知,这两个量纲为一参数并不能涵盖阵列圆孔射流的所有结构参数,如采用平板开孔、短圆管和长圆管的结果就有显著差异[18],此外射流废气的排出方式,如强制排气、排气不畅、排气良好对换热系数也会影响显著[19]。因此Martin的回归公式与Glaser[20]的实验值存在明显偏差,当Re>20 000 时 , Glaser 的 努 谢 尔 数 高 出 回 归 值 约20%~30%,当 Re<20 000 时,Ott[21]的实验结果也高出Martin 公式计算值的25%左右。Meola 等[22]也曾指出Gardon的实验值与Martin 公式的计算值差异较大,Gardon的实验值较大。可见,目前还难以获得通用的圆孔阵列射流换热准数方程。
近年来,随着电子工业和制造业等的发展,气体冲击射流冷却需要更高的换热系数和更好的均匀性,如带钢热处理领域生产高强度钢板所需的平均换热系数可达1 000 W/(m2·K)。这意味着一方面需要进一步提高雷诺数,另一方面需要进一步优化冲击射流阵列结构参数,例如采用密集型的气体射流装置。王磊等[23]研究了涡轮叶片用密集冲击射流冷却的换热情况,考察了小喷嘴间距条件下的换热性能。Meola[22]测量了方形、圆孔等喷嘴的密集冲击射流换热系数,结果表明换热系数比Martin 公式计算值高出20%左右。
本文针对刀片式密集圆孔气体冲击换热进行实验研究,以得到平均对流换热系数,用于指导冷却装置的开发、设计与运行。
1 实验部分
1.1 实验原理

图 1 刀片式圆孔射流装置Fig. 1 Blade-type circular jet device
图1 所示为刀片式圆孔射流装置,喷孔布置在狭长型的刀片状肋管上,类似于狭缝喷嘴,肋管之间形成规则的狭长形逸气通道,排气空间较大;在肋管头部布置间距为Yn、直径为D 的圆孔,相邻肋管的间距为Xn。这种结构使得刀片式圆孔气体射流装置兼具狭缝喷嘴和圆孔喷嘴的优点,一方面肋管的集气功能可以大幅降低供风和集气环节的阻力损失,在风机功率一定的情况下可以提高气体流量;另一方面良好的排气空间,使得喷孔可以密集布置,提高了开孔率。
刀片式圆孔气体射流换热均匀,其测量原理如图2 所示。射流速度为ug,温度为Tg的气体从冲击高度为H 的刀片式多排圆孔喷嘴喷射出来,垂直向下喷射到温度为Ts的高温薄铜板上进行强化换热。由于铜板厚度极薄,毕渥数(Bi)不超过0.01,忽略其厚度方向的温度差别。高温薄铜板背部黏贴有电压为U、电流为I 的薄膜电阻加热器供热。射流气体与薄铜板换热后,废气流向相邻肋管间的逸气空间,最终从两侧排出。当薄铜板表面温度稳定在Ts后,薄铜板与气体的换热满足如式(1)所示的热平衡式:

图 2 刀片式圆孔气体射流测量原理示意图Fig. 2 Schematic diagram of measurement for blade-type circular gas jets

式中:kg和vg分别为气体的导热系数和运动黏性系数,单位分别为W/(m·K)和m2/s;定性温度采用气体喷口处的温度值Tg。改变射流速度和喷射高度,测量各工况下的平均对流换热系数,可以获得NuDav与ReD的关系。
1.2 实验装置
图3 所示为圆孔气体射流实验原理,主要分为空气管路系统、刀片式喷嘴喷射系统、冲击板与热流密度测试系统、位置调节系统和信号采集系统。
室温空气经过滤器和消音器后由压头为12 000 Pa,风量为3 600 m3/h 的离心式风机鼓入直径400 mm 的风管,经主管道上的调节阀和孔板流量计后进入风箱。在风箱前,管道逐渐由圆管缓慢过渡到风箱上矩形接口,以保证气体流量在喷嘴组上均匀分配。
刀片式圆孔喷嘴的具体尺寸如图4所示,结构参数包括喷孔直径D、肋管深度E、喷嘴纵向间距Xn、横向间距Yn(见图5)、喷射高度H 和喷嘴个数n。开孔率(Af)表示喷嘴出口总面积与换热面总面积的比值,图5 中分别示出了狭缝喷嘴(5(a))、等间距圆孔喷嘴(5(b))和刀片式圆孔喷嘴(5(c))的开孔率定义。刀片式圆孔喷嘴的具体几何尺寸如表1 所示,其开孔率高达0.036 6,是常规管式风箱开孔率的3 倍,接近狭缝喷嘴的开孔率。当 D=8 mm 时,如果带钢与喷嘴间距过小,例如 H/D <5,则带材振动容易损坏喷嘴,将不具备实际用途;如果带钢与喷嘴间距过大(H/D >15),则会造成风机的动力浪费。由于刀片式圆孔射流的应用场景为带材连续退火,考虑到带材顺利运行和喷嘴效率,选取6<H/D<13,具体为6.25、7.50 和 12.5。

图 3 圆孔气体射流实验原理Fig. 3 Experimental apparatus for circular gas jets
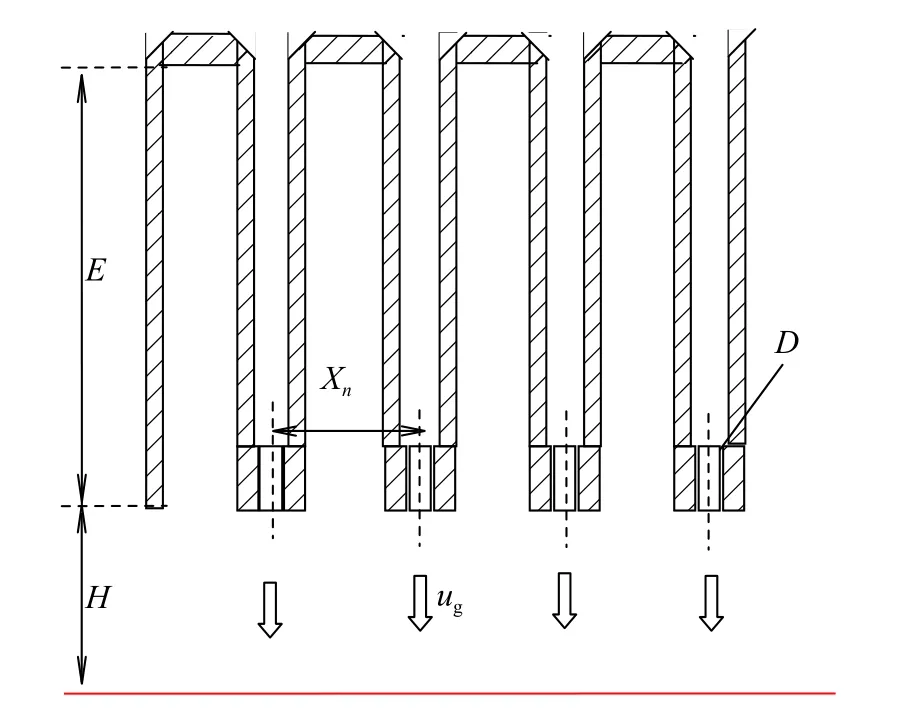
图 4 刀片式圆孔喷嘴几何结构Fig. 4 Geometric drawing of blade-type circular nozzle

图 5 不同喷嘴布置方式下的开孔率Fig. 5 Af for different nozzle configurations

表 1 刀片式圆孔喷嘴的几何尺寸表Table 1 Geometric data for blade-type circular nozzle
冲击板的作用是模拟气体射流冲击后形成的流场,其材质为不锈钢,几何尺寸为600 mm×600 mm×8 mm。在冲击板的中央镶嵌着边长250 mm 的方形薄铜板,其作用是模拟高温带材表面与气体射流的换热,并测定平均热流密度。高温薄铜板与冲击板之间填充厚约10 mm 的绝热材料,以减小薄铜板边缘与冲击板之间的接触导热,安装时使薄铜板上表面与不锈钢冲击板面保持在同一平面上。
总管冷却气体的流量采用孔板流量计测量,误差约为3%。铜板温度采用T 型热电偶测量,测温范围0~350 ℃,最大温度误差为0.5 ℃;气体温度采用水银温度计测量,测温范围0~100 ℃,最大温度误差为0.2 ℃。电压表为1.0 级,测量范围0~200 V,最大误差为2 V。根据误差分析[24],可得雷诺数的相对误差为3%,平均努谢尔数或平均对流换热系数的相对误差为

2 结果与讨论
2.1 平均换热系数
采用的刀片式圆孔喷嘴组横向与纵向间距较小(Xn/D=6.25, Yn/D=3.125),局部对流换热系数可视为均匀分布,采用薄铜板热流计表面的平均温度来计算平均努谢尔数NuDav。但实际上,换热系数在空间上仍然存在一定的不均匀性,如果采用表面温度的最高值和最低值估算努谢尔数的最大值NuDav_MAX和最小值NuDav_MIN,它们与平均努谢尔数NuDav的偏差可以表征换热系数在空间上的不均匀程度。图6示出了H/D =7.50 时,以NuDav_MAX-NuDav为正偏差、NuDav-NuDav_MIN为负偏差的 NuDav与 ReD的对应关系。由图6 可以看出,当雷诺数较高时,NuDav的偏差较大,但是最大偏差仍小于5%,平均偏差为2%。由此可见,可以采用热流计的平均温度估算NuDav。
图 7 示出了不同 H/D 条件下 ReD对 NuDav的影响,主要研究了 H/D 分别为 6.25,7.50 和 12.5 时的3 种情况。由图7 可以看出,NuDav随雷诺数的增加而增大,即换热系数随着喷气速度的增大而增加。表明提高射流速度会使气体射流与冲击面的动量交换加剧,从而增强换热效果。由图7 还可以看出NuDav对 ReD的依赖程度。3 种 H/D 条件下,在双对数坐标下,实验点均落在3 条近乎平行的线附近,表明3 种H/D 条件下准数方程中ReD的幂次接近。当H/D<7.50 时,喷射高度的影响并不明显,当H/D>7.50 时,增加喷射高度会显著降低换热系数。

图 6 不同ReD 下平均努谢尔数NuDav 的测量偏差Fig. 6 Measured derivation of NuDav at different ReD
图 8 示出了 N uDav/R(其中 m 为指数)与量纲为一喷射高度 H /D 的关系,按照(NuDav/RemD)∝(H/D)p(其中p 为指数)的形式进行回归,可得到 p =-0.606 ,说明 NuDav随 H /D 的-0.606 次幂递减。

图 8 量纲为一喷射高度H/D 对 N uDav/RemD 的影响Fig. 8 Effects of normalized impingement height H/D on NuDav/RemD
2.2 与已有准数方程的比较
在 6 000≤Rex≤600 000, 8≤Xn/D≤32 条 件 下 ,Gardon 获得的准数方程如下[11]

式中,ua为到达冲击面的速度,m/s,考虑了喷射高度的影响。Martin 总结的准数方程为[12]


公式的适用范围为 2 000≤ReD≤100 000,2≤H/D≤12,0.004≤Af≤0.04。
图9 比较了H/D =7.5 时函数的测量值与Gardon公式的计算值,可以看出两者吻合很好。
图10(a)比较了H/D =7.5 时函数的测量值与Martin 公式的计算值,可以看出测量值明显高于Martin 公式的计算值,前者大约是后者的1.4 倍左右。这与Glaser[20]和Ott[21]实验结果与Martin 公式的比较结果是一致的。

图 9 H/D=7.5 测量值与Gardon 公式比较Fig. 9 Comparision of measured data with values reduced by Gardon’s equation when H/D =7.5

图 10 H/D =7.5 时实验值与 Martin 公式(a)和修正 Martin 公式(b)结果比较Fig. 10 Comparision of measured data with values reduced by Martin’s equation (a) and corrected Martin’s equation (b) when H/D=7.5
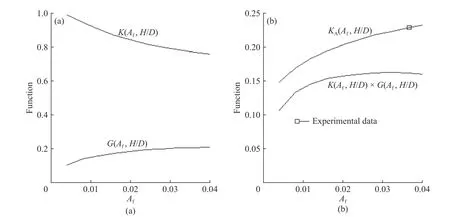
图 11 H/D =7.5 时函数 K(Af,H/D)、G(Af,H/D)和修正函数 KA(Af,H/D)以及函数 K(Af,H/D)× G(Af,H/D)与 Af 的关系Fig. 11 Relationship between function K (Af,H/D),G (Af,H/D) and modified KA (Af,H/D)、function K (Af,H/D) × G (Af,H/D) with Af whenH/D=7.5
图 11 示 出 了 H/D=7.5 时,函 数 K (Af,H/D) 、G(Af,H/D) 及修正函数KA( Af,H/D) 分别与Af的关系。由图 11(a)可以看出,当 H/D=7.5、Af>0.03 时函数 K (Af,H/D) 和 G (Af,H/D) 几乎不变化;由图11(b)可以看出,当 Af>0.02 时,函数 K (Af,H/D) ×G(Af,H/D)几乎不变化。这主要是Martin 公式中函数K(Af,H/D)和 G (Af,H/D) 过度压制了开孔率Af的作用。
如果引入修正函数

3 结 论
(1)以空气为模化介质,考察了刀片式多排圆孔冲击射流换热情况,结果表明平均努谢尔数随雷诺数的增加而增大,与量纲为一喷射高度 H /D 的0.606 次幂成反比。
(2)刀片式多排圆孔气体射流采用密集布置喷孔后,提高了开孔率,换热系数显著提高,约为Martin公式计算值的1.4 倍。
(3)实验结果与Gardon 公式非常吻合,与Martin公式存在显著差别,引入修正的KA(Af, H/D)函数后两者吻合较好。

