基于AEKF的永磁同步电机转速控制方法

党 克，刘子源，田 勇，衣鹏博,刘 闯

(东北电力大学现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林 132012)

0 引 言

随着电力电子技术和稀土永磁材料取得突破性进展，永磁同步电机(以下简称PMSM)现代控制理论体系越来越完善，PMSM逐渐显现出自身的优势，比如便于安装和维修，运行高效，具有较小的转矩脉动和较高的气隙磁密，广泛应用于航空航天、军用武器跟随系统以及新能源汽车等行业[1]。在大多数实际应用中，PMSM控制需要位置传感器来保证转速控制精度。但是，位置传感器存在维护成本高、空间限制和抗干扰性差的缺点，并且会受到湿度和腐蚀等条件的影响，在PMSM控制领域，越来越多专家和学者致力于研究无速度传感器。

现阶段，针对PMSM转子位置和转速估计，陆续出现了SMO(滑模观测器)、MRAS(模型参考自适应系统)、神经网络法、EKF(扩展卡尔曼滤波法)等手段。SMO方法的优点在于具有良好的鲁棒性，便于实现，缺点是对电机相关参数估计不稳定[2]。在无传感器控制领域，MRAS方法的应用越来越广泛，由自适应率、参考模型、可调模型组成控制策略，但可能难以适应参数，鲁棒性较差[3]。神经网络法有效地提高了电机控制系统的精度和稳定性，但其计算量大，实际应用尚不成熟[4]。

EKF可以有效地处理非线性系统，并且能够边采集数据边计算，同时EKF也具有合理的收敛速度。EKF算法适用于电机控制系统，可以工作在较大的速度范围内，甚至在较低的速度下能够完成转速估计。这些特性使EKF在PMSM的无传感器速度控制应用中备受关注[5-7]。近年来，对EKF进行了广泛的研究。测量和系统噪声协方差矩阵R和Q的确定对用EKF进行估计有重大影响。通常用试错法来假设这些协方差矩阵,耗时长，且常数噪声矩阵并不能代表实际噪声矩阵，使得EKF精度下降[8]。为提高算法精度，获得噪声矩阵的最佳值，文献[9]利用差分进化算法获得了噪声矩阵的优化值。此外，文献[10]设计了自适应衰落EKF来寻找Q和R的值，但是该方法需要离线完成，通常耗时很久。Sage-Husa自适应滤波具有原理简单、快速跟踪系统噪声和测量噪声统计特性的优点,在惯性导航中应用广泛[11]。

为此，本文根据传统EKF测量噪声和系统噪声矩阵不能自适应调节的问题，研究了一种将改进的Sage-Husa自适应卡尔曼滤波算法和基于新息的自适应扩展卡尔曼滤波算法相结合的方法，提高系统的观测精度，改善系统的稳定性。

1 PMSM数学模型

PMSM可以选择d,q同步旋转坐标系下的数学模型，也可以选择α,β静止坐标系下的数学模型，在d,q同步旋转坐标系模型下，变换矩阵中含有转子磁链空间角度的正余弦函数，造成递推计算时间的增加。α,β静止坐标系相对于旋转坐标系可节省EKF计算时间，缩短采样周期，提高估算精度。因此，本文建立表贴式三相PMSM的数学模型。在静止坐标系下的电压方程：

(1)

式中：uα为定子电压的α轴分量；uβ分为定子电压的β轴分量;iα为定子电流的α轴分量；iβ为定子电流的β轴分量;Rs为定子电感；Ls为定子电感；ψf为永磁体磁链；ω为电机的机械角速度；θ为转子位置角。

将式(1)用电流方程的形式表示，可得：

(2)

对于PMSM来说，相比电气时间常数，机械时间常数更大，通常用ωe表示对转子位置求导的结果，用0表示电机速度变化量，可提高计算过程的便利性，即：

(3)

可以得到状态方程如下：

(4)

式中：

(5)

考虑到系统噪声和测量噪声的影响，且式(4)是非线性的，构建PMSM离散化的数学模型:

(6)

式中：Wk-1为系统噪声；Vk为测量噪声。且这两个噪声都是零均值的白噪声。通过测量噪声协方差矩阵R和系统噪声协方差矩阵Q代入EKF递推算法，并不直接利用噪声矢量W和V，假设V和W不相关，且初始状态x(0)也不相关于Vk和Wk-1。

2 自适应EKF观测器设计

EKF是线性系统状态估计的卡尔曼滤波器在非线性系统中的扩展应用。通过对系统状态进行在线估计，进而实现对系统的实时控制。EKF涉及预测和校正两个阶段。使用当前时刻的系统测量输出，可以预测下一时刻的系统状态。使用实际输出和预测输出中的误差校正这些预测状态。具体步骤如下：

(7)

(8)

Kk=Pk|k-1CTSk

(9)

Pk|k=(I-KkC)Pk|k-1

(10)

xk|k=xk|k-1+Kk(yk-xk|k-1)

(11)

2.1 测量噪声估计器

根据理论分析及实验探究,在EKF估计PMSM转速时,其主要的不足之处是不能准确地描述协方差矩阵的统计特性，包括噪声协方差矩阵和测量协方差矩阵。长期以来，科学家利用试凑法对协方差矩阵统计特性进行估计，估计结果的精确性以及估计算法的收敛性很大程度上取决于选取的参数是否合理。本文利用自适应扩展卡尔曼滤波(以下简称AEKF)进行估计，改进的Sage-Huse AEKF用来估计测量噪声，基于新息的卡尔曼扩展自适应[12]方法用来估计系统噪声。由于噪声协方差矩阵和测量协方差矩阵会随着系统参数改变而发生变化，因此能有效提高统计特性估计结果的精确度，从而具有良好的收敛性，同时保证了系统参数鲁棒性。

对于时变系统，利用Sage-Husa AEKF构建以下噪声估计器：

(12)

(13)

ek=yk-Cxk-1|k-1-rk

(14)

式中：b表示遗忘因子，其取值范围为0.95～0.99；ek是Sage-Husa滤波器残差；rk是测量噪声的平均值。

式(12)中的主要缺点是矩阵的减法。实际上，这种减法可以使式(8)中的矩阵几乎是奇异的，甚至是非正定的，使得滤波器系数发散。因此，本文用基于残差估计代替式(12)中的Rk递归估计，这将增加滤波器的稳定性。使用卡尔曼滤波器中的新息残差：

vk=yk-Cxk-1|k-1

(15)

所以式(12)改写：

(16)

2.2 系统噪声估计器

通过取长度为N的窗口先前残差序列的平均值来导出新息残差的协方差估计：

(17)

式中：j0=k-N+1是估计窗口中的第一个样本。

估计的系统噪声协方差矩阵：

(18)

式中：Δx=xk|k-1-xk-1|k-1。

等式根据稳态条件下的新息顺序，可将式(18)描述如下：

(19)

Sage-Husa自适应滤波法最大的缺点在于无法同时获得测量噪声和系统噪声的观测结果，本文的AEKF在控制周期中，系统可以在稳定的前提下观测到这两类噪声。

3 仿真分析

3.1 模型框图

图1为基于AEKF的PMSM无传感器控制系统框图。其控制方式采用id=0的控制策略。控制结构采用双闭环控制结构，转速环为外环，电流环为内环。将uα,uβ,iα,iβ作为AEKF算法的输入信号，将估算出的ω,θ作为矢量控制反馈控制。

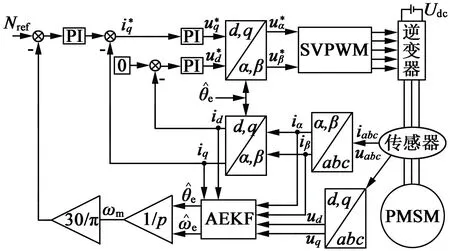
图1 基于AEKF的PMSM无传感器控制系统框图

3.2 仿真验证

本文分别对EKF和AEKF两种算法进行仿真实验，预定转速为500 r/min，仿真持续时间0.5 s。表1给出了PMSM的相关参数，两种算法的转速估计值如图2所示，两种算法的转子位置估计值如图3所示。

表1 电机参数

由图2(a)可知，传统EKF算法在初始阶段转速超调，超调量为13%，最大转速误差为60r/min，在0.18s到达预定转速后，转速波动为10r/min。

由图2(b)可知，AEKF算法在初始阶段几乎没有转速超调，超调量仅为1%，最大转速误差为40r/min，在0.14s到达预定转速后，转速波动为5r/min。

由图2可以得出，AEKF算法响应快，追踪效果好，在进入预定转速时，AEKF收敛性要优于EKF，估计转速更接近电机的实际转速。

(a) 基于EKF转速估计

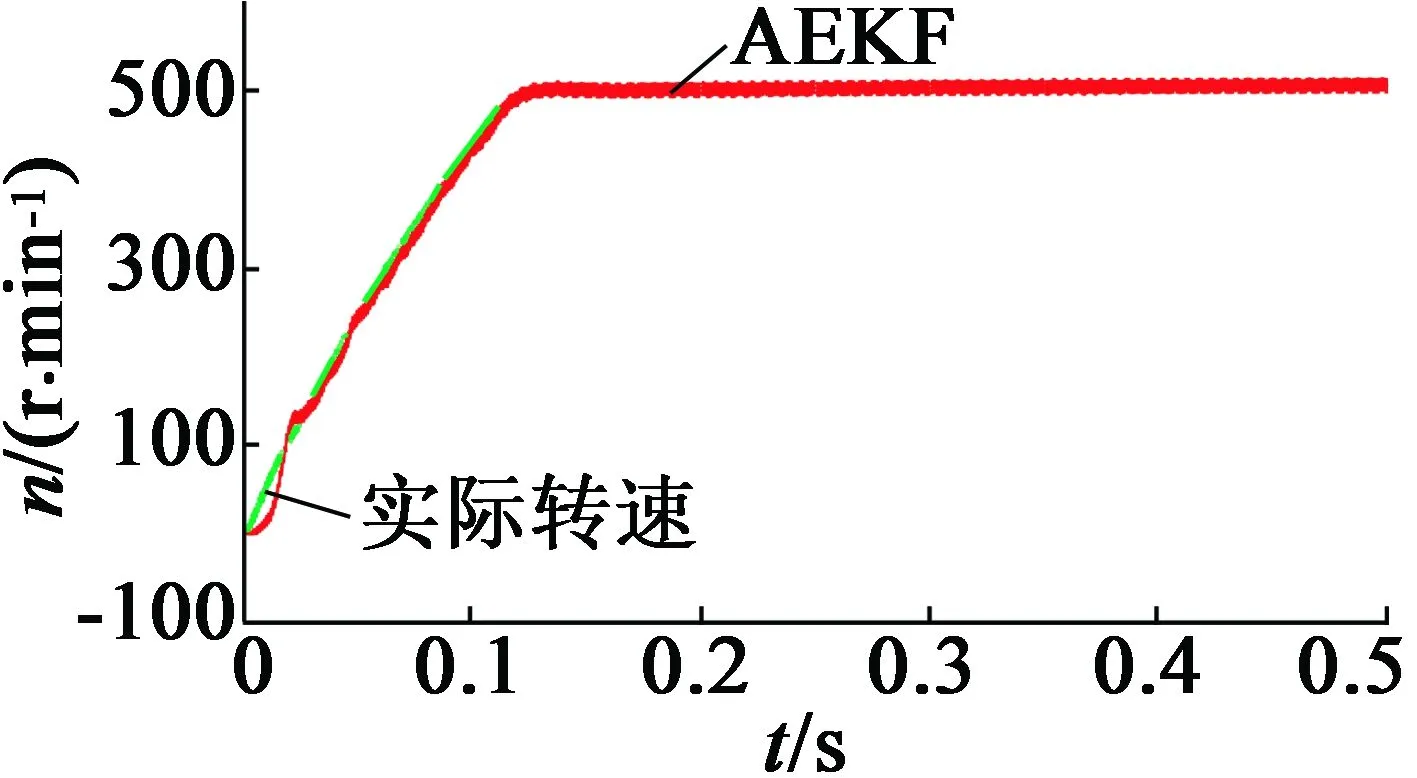
(b)基于AEKF转速估计

由图3可以看出，AEKF相比于传统的EKF，对电机转子位置的估计值精确度更高，传统EKF算法对转子位置的估计值稍滞后于实际值。由图3(c)、图3(d)放大图可以看出,AEKF算法最大位置误差比传统EKF算法减小7%，更接近于转子实际位置。

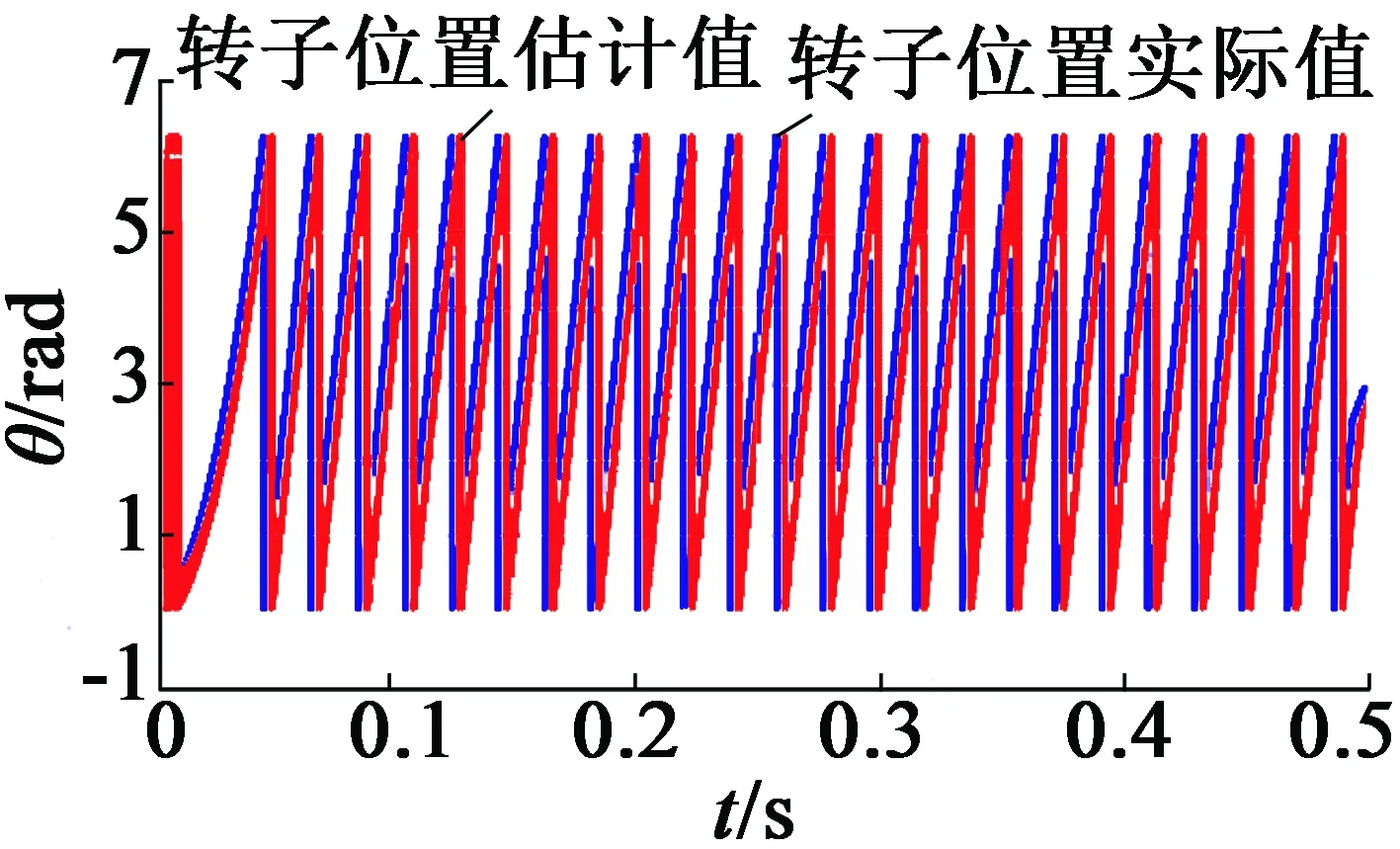
(a) 基于EKF转子位置估计

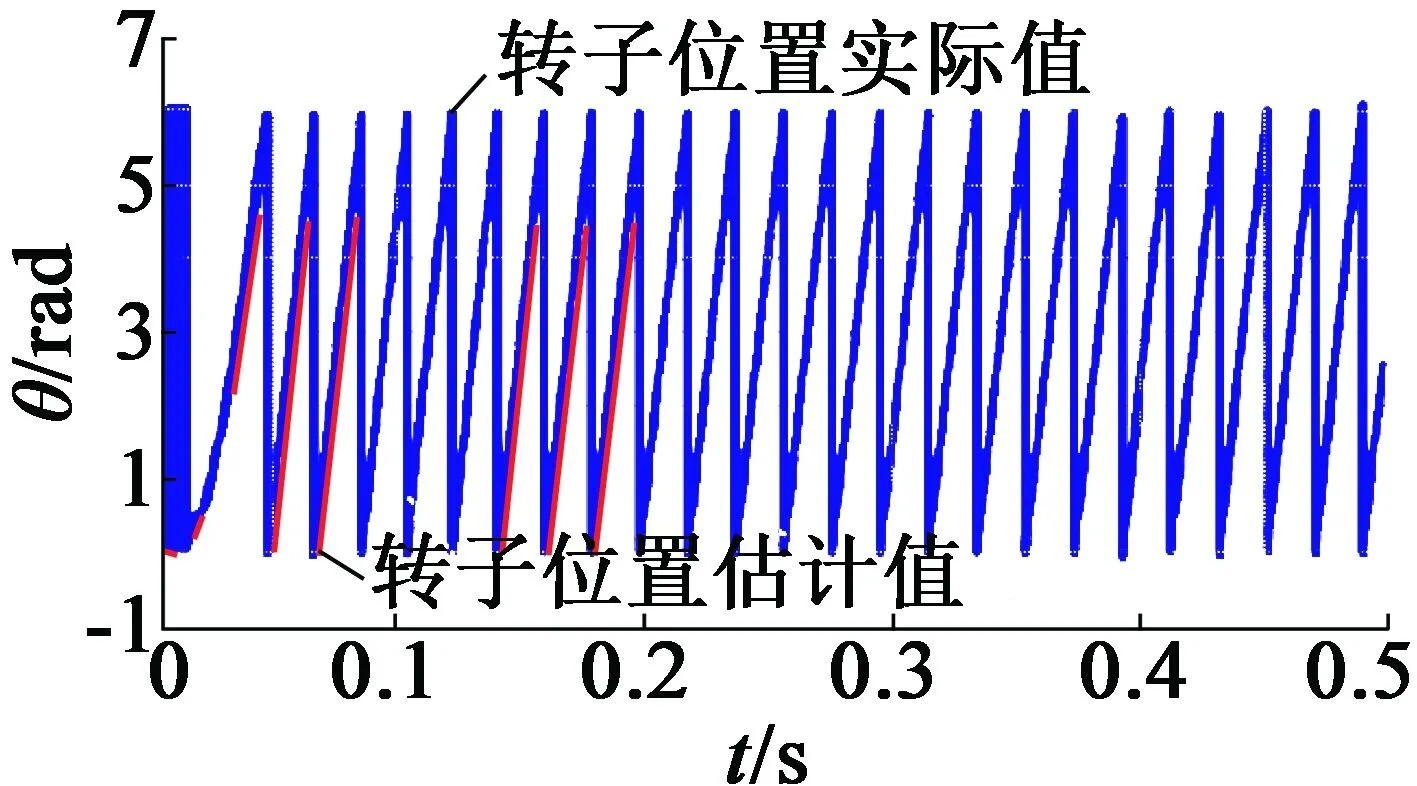
(b)基于AEKF转子位置估计

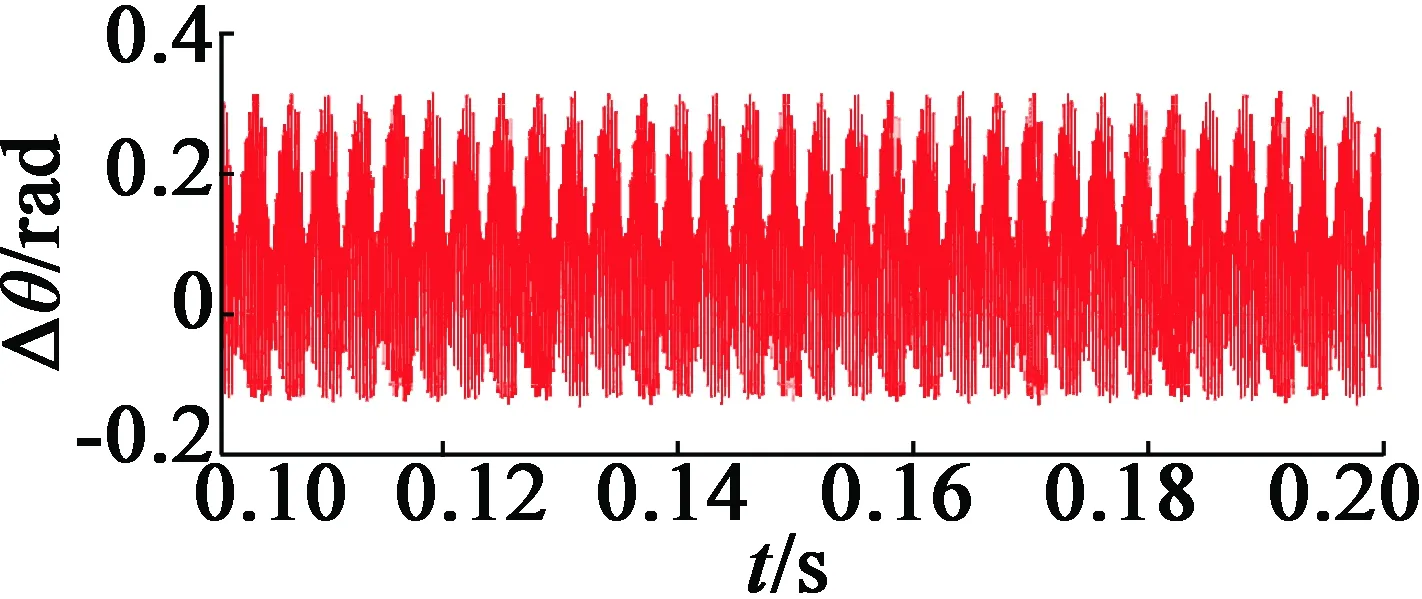
(c) 0.1～0.2 s时基于EKF转子位置估计误差放大图

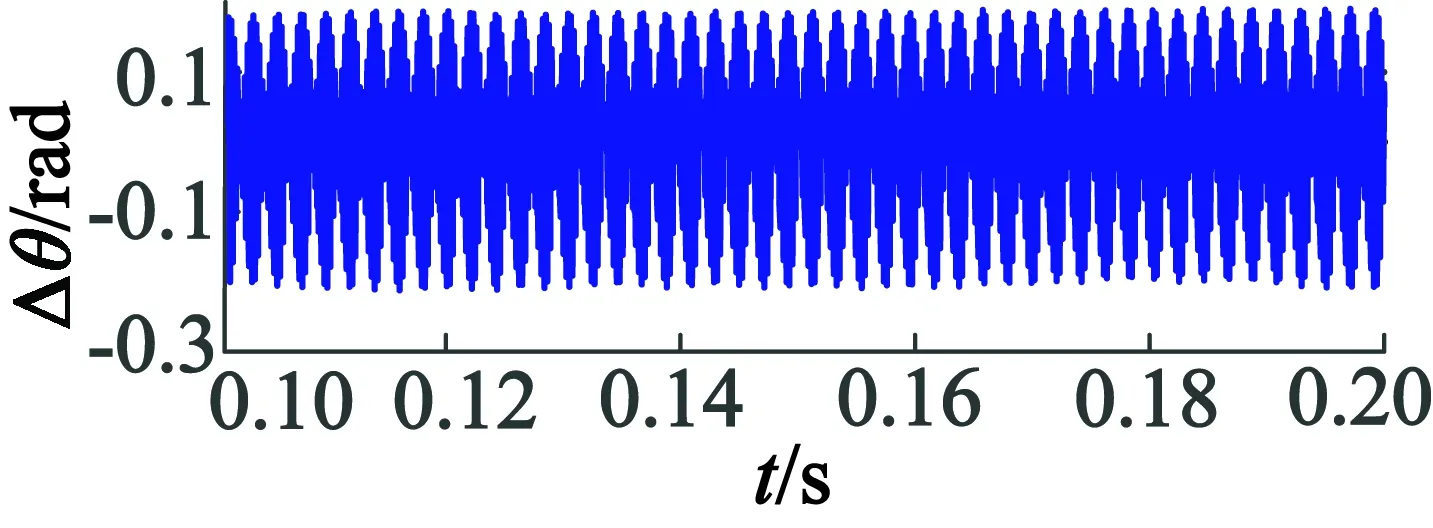
(d)0.1～0.2 s时基于AEKF转子位置估计误差放大图

3.3 参数鲁棒性

近年来，电机控制系统已经广泛应用于实际工程中，在电机起动的瞬间，电感、定子电阻额定值与实际值的差值很小。随着电机运行时间的增加，内部温度会逐渐上升，电子电感和电阻都会随之上升，严重影响电机控制的精确度。针对上述问题，本文在开展AEKF算法参数鲁棒性实验的过程中，规定定子电感值和电阻值分别是1.1倍和1.2倍的额定值。图4和图5给出了仿真结果。

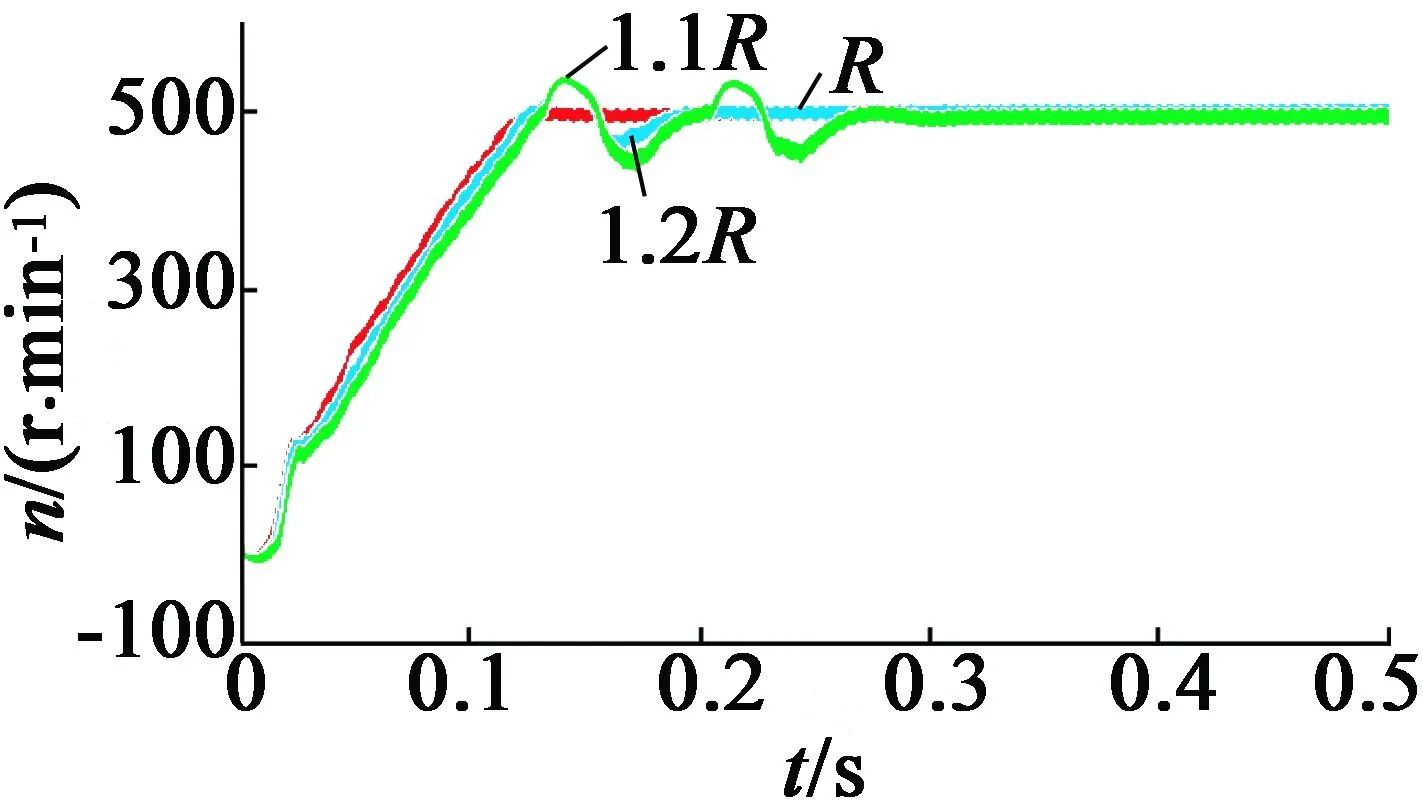
图4 定子电阻为1倍，1.1倍，1.2倍时的仿真结果

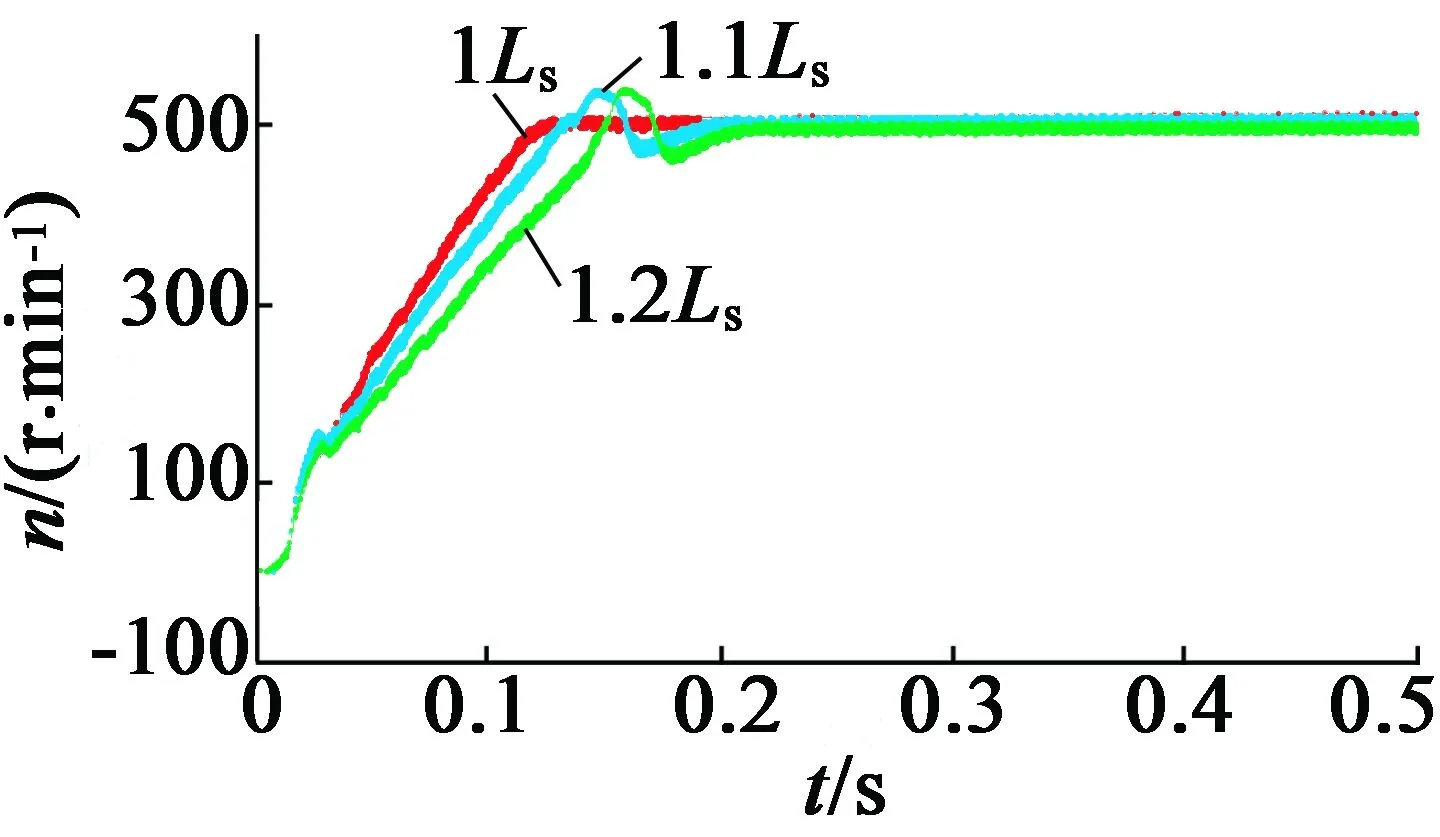
图5 定子电感为1倍，1.1倍，1.2倍时的仿真结果

从图4可以看出，当定子电阻取值是其额定值的1.1倍和1.2倍时，用AEKF算法的转速波动的时刻是0.1～0.2s，波动幅度达到±50 /min，并随着时间的推移逐渐趋于收敛，收敛值是500r/min；当定子电阻取值是其额定值的1.2倍时，用AEKF算法的转速波动的时刻是0.1～0.25s，波动幅度达到±50r/min，并随着时间的推移逐渐趋于收敛，收敛值仍然是500r/min。

从图5可以看出，定子电感增加0.1倍后，AEKF算法在0.1～0.2s时转速出现±50r/min的波动，虽然到达预定转速的时间有所增加，但是最后收敛至500r/min。

根据图4和图5不难发现，AEKF算法的参数鲁棒性较好，能有效解决PMSM无传感器控制估计值不准确的问题。

4 结 语

本文研究了一种AEKF算法，将改进的Sage-Husa自适应卡尔曼滤波算法和基于新息的AEKF算法相结合，以解决EKF测量噪声和系统噪声矩阵不能自适应调节的问题，相比于传统EKF算法，本文采用的AEKF算法对转速和转子位置估计精度更高，收敛性更好。从理论和仿真实验两方面证明了AEKF算法的稳定性和参数鲁棒性。