分数槽集中绕组表贴式永磁同步电机电感参数研究
王 璐,许雪峰
(1.沈阳航空航天大学 电子信息工程学院,沈阳 110136,2.沈阳工业大学 电气工程学院,沈阳 110870)
0 引 言
分数槽集中绕组永磁同步电机具有以下优点:高功率密度,高效率,节约成本,恒功率区间弱磁扩速能力优越及容错能力强,低速运行时不用过多考虑定、转子斜槽、斜极等降低齿槽转矩措施。因此,其在高速和低速直驱应用场合得到广泛应用[1-2]。但是,采用分数槽集中绕组后,其绕组磁动势在电机气隙空间内分布着幅值较大的次谐波以及绕组系数与基波相同的高次谐波[3],可能造成电机振动噪声增大、转子损耗提高,并导致电机发热严重等不良后果。现阶段,分数槽集中绕组永磁同步电机的关键技术研究和应用已引起了广泛关注,且在不同的应用领域取得了较大的进展和成效[3-5]。但对于分数槽集中式单、双层绕组的永磁同步电机电感参数进行综合分析研究,且阐述其相互联系和变化规律的文献目前较少。
文献[6]分别开发了10极12槽单、双层绕组的表贴式永磁同步电机,运用理论分析和实验测试对电感参数进行研究,且理论分析与实验测试结果误差在±5%以内。同时,分析结果表明,10极12槽永磁电机的互感接近于零。文献[7]基于绕组函数法对双层集中式绕组永磁同步电机自感、互感进行论述,研究了永磁电机整数槽绕组和分数槽集中绕组之间的电感参数关系,测试了多台不同转子磁极结构永磁电机的交、直轴电感参数,总结了不同磁极结构的电机凸极率特性。
分数槽集中绕组永磁同步电机与每极每相槽数分布式绕组的永磁同步电机相比,其有效材料利用率和容错性能等方面得到一定改善。同时,分数槽集中绕组以其自身较高的自感参数限制了短路电流。基于上述分析,分数槽集中绕组表贴式永磁同步电机电感参数的准确计算、解析法与有限元法的对比分析、电感参数统一解析表达式的推导、相应规律特性的归纳总结是十分重要的。为证明其理论正确性,通过实验进行验证。
1 电感分析
本文基于绕组函数法对分数槽集中绕组单、双层表贴式永磁同步电机电感参数进行研究,利用数学表达式阐述两者之间关系及变化规律。分数槽集中绕组永磁同步电机是由m个(m=1,2,3,…)单元电机组成,且在圆周方向(旋转电机)成周期性分布。图1为单层、双层绕组排布的30极36槽表贴式永磁同步电机。
1.1 绕组函数法自感分析
绕组函数法[7]主要分析永磁同步电机的自感、互感参数。该方法中自感参数的描述为电机相匝数函数与其线圈匝数的匝链在空间角度范围内的积分后与气隙磁导的乘积;互感参数的描述为相匝数函数与其不同相线圈匝数函数的匝链在空间角度范围内的积分后与气隙磁导的乘积。计算方法如下:
(1)
(2)
式中:μ0为真空磁导率,μ0=0.4π×10-6H/m;r为气隙半径;lef为铁心有效长度;g0为气隙长度;nA(θ)为A相绕组的匝数函数的空间分布;NA(θ)为A相绕组的绕组函数的空间分布,其波形与A相绕组磁动势波形相同。
本文以30极36槽单、双层永磁电机为例,对其自感参数进行研究,且以双层自感作为基值,总结出单、双层永磁电机自感比值变化规律。分析前,假设两种绕组形式的永磁同步电机的转子完全相同,并保证其气隙长度相同,忽略槽开口对气隙磁场影响。算例中两台电机永磁磁链分别为ψ1,ψ2:
(3)
(4)
式中:N为线圈匝数;p为极对数;q为每极每相槽数;τ为极距;Bm1为空载气隙磁通密度基波幅值。其中,对于30极36槽单层、双层绕组形式的每极每相槽数q1=q2;令ψ1=ψ2,进而分析比较出N1=1.93N2。为分析方便,现假设N1=1,即得到30极36槽单层、双层绕组永磁同步电机绕组函数空间分布,如图2所示。
因此,30极36槽单、双层集中绕组永磁电机自感参数计算可根据式(1)进行分析。
(5)
(6)
通过上述分析计算,30极36槽单层、双层A相自感的比值为1.87。由此可以看出,采用单层绕组时直轴同步电感最大,短路故障时抑制短路电流效果更好。
30极36槽单、双层每相自感的计算只是个例,为分析其普遍性,下面对三相永磁同步电机在Q=2p±2时的每相自感进行统一归纳总结。式(7)为分数槽集中绕组单、双层每相自感统一表达式:
(7)
式中:n=1代表单层绕组,n=2代表双层绕组。分数槽集中绕组单、双层绕组自感比值关系式如下:
(8)
式中:kdp1(1)和kdp1(2)分别为单、双层分数槽集中绕组的基波绕组系数。
由此可见,利用式(7)可以计算分数槽集中绕组的每极每相槽数q不同时的自感。同时,通过式(8)可以得出Q=2p±2时单、双层自感比值在1.8~2之间。定子槽数相同时,Q=2p+2的自感小于Q=2p-2的自感。
通过上述可知,基于绕组函数法可以计算出表贴式永磁电机的自感和互感,进而可以求取直轴电感Ld,即Ld=LAA-(LAB+LAC)/2,30极36槽永磁电机绕组互感理论分析LAB=LAC=0。此处Ld的计算只计及电枢反应电感和谐波漏感的影响。
1.2 槽漏感分析
文献[2]提到绕组总电感包括基波电枢反应电感、谐波漏感、槽漏感、端部漏感(由于端部漏感较小,本文暂不予以考虑),可见,槽漏感的计算至关重要。槽漏感计算[6,8]表达式如下:
(9)
式中:Ns为每槽导体数;hs为槽深;Ws为槽宽;h0为槽口高;b0为槽口宽。30极36槽单、双层每相槽漏感计算如下:
(10)
(11)
式中:Ws1=Ws2。根据式(3)和式(4)可知,N1=1.93N2。以双层绕组每相槽漏感作为基值,则分数槽集中式单、双层绕组每相槽漏感比值如下:
(12)
通过式(12)计算可知,分数槽集中式单、双层绕组的每相槽漏感近似相等。现推导其一般表达式,分别如式(13)、式(14)所示,其单、双层每相槽漏感的一般比例关系表达式如式(15)所示。
(13)
(14)
(15)
通过计算Q=2p±2每相槽漏感比值ks相可以看出,其数值在1.33~0.98之间变化。并且,随着Q增大,其每相槽漏感比值减小。
基于上述分析,本文以22 kW 30极36槽表贴式永磁电机为例,对其解析计算研究。该电机主要尺寸如表1所示。表2为电感解析计算结果。
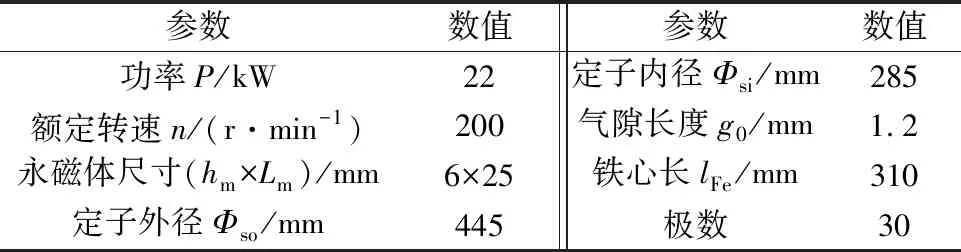
表1 电机的主要参数

表2 22 kW 30极36槽电感解析计算
从表2看出,22 kW 30极36槽的单层绕组的谐波漏感较双层绕组谐波漏感大,且单、双层槽漏感相对于同步电感的占比也较大。因此,为证明该解析计算的正确性,下文通过电磁场计算分析和实验进行验证。
2 基于有限元法同步电感分析
基于有限元方法,通过Maxwell 2D仿真模型分别计算单、双层绕组永磁电机的d轴和q轴同步电感Ld和Lq(忽略绕组端部电感影响)。为求取单、双层绕组的谐波漏感和槽漏感,需将同步电感Ld和Lq分别与电枢反应电感Lad和Laq作差,即为单、双层绕组的定子漏感Lν+Ls,并以22 kW 30极36槽双层永磁电机为例进行详述。
首先,根据坐标变换基本理论求取d轴和q轴的同步电感Ld和Lq[9]。将Maxwell 2D中的A相绕组轴线与d轴重合,即θ=0,并根据式(16)和式(17)分别在ABC三相绕组中通入iA,iB和iC。通过电磁场计算将获取的自感和互感的结果代入式(18)求取Ld和Lq。经上述分析计算,22 kW 30极36槽双层永磁电机的Ld和Lq分别为10.876 mH和10.708 mH。通过与表2中解析计算的Ld对比可知,有限元计算的Ld偏小,且误差为-5.5%。原因是解析法未计及槽开口对气隙的影响,使得其Ld计算值偏大于有限元法的计算结果。图3为22 kW 30极36槽双层永磁电机的磁场分布。
(16)
(17)
Ldq=CTLABCC
(18)

(a) 空载

(b) 负载
其次,计算22 kW双层永磁电机的电枢反应电感Lad和Laq。计算Lad时,A相绕组轴线与d轴重合,给定电流为Imax,B相和C相均给定-0.5Imax。由此得到直轴电枢反应气隙合成磁场波形,并将空载气隙磁场波形与之作差得到直轴电枢反应气隙磁场波形,如图4(a)所示。将图4(a)直轴电枢反应气隙磁场波形进行谐波FFT分解,如图4(b)所示。提取图4(b)直轴电枢反应气隙基波磁密求取Ead;Laq计
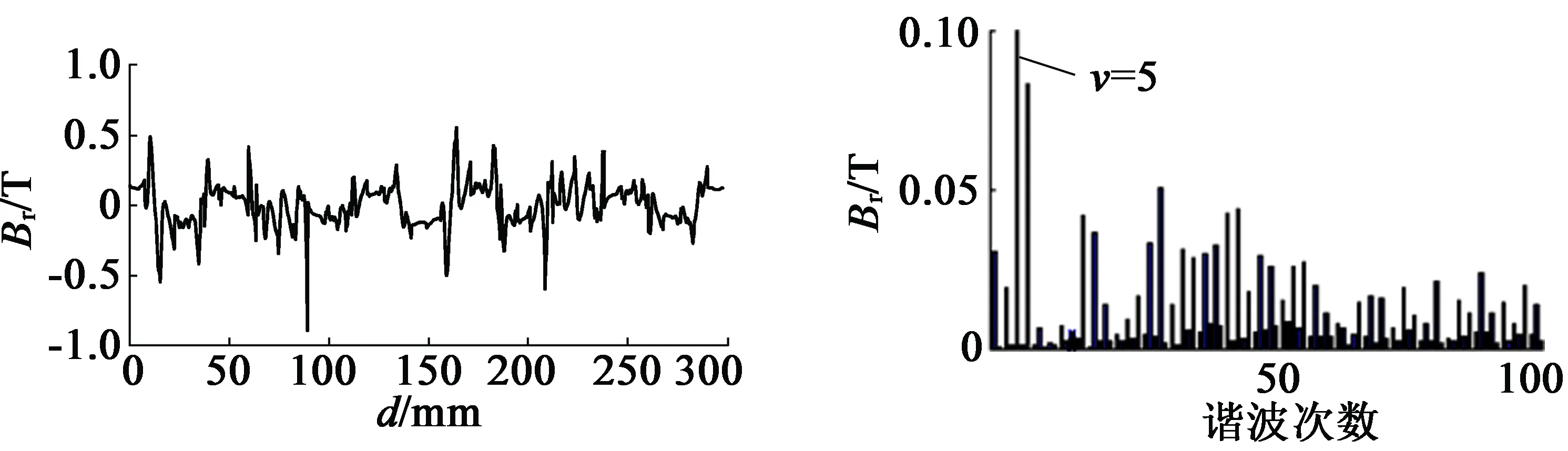
(a) 气隙磁场波形 (b) FFT分解
算时,A相电流设置为零,B相与C相电流分别给定Imax和-Imax。将计算出的负载气隙合成磁场波形与空载气隙磁场波形相减,可以得到交轴电枢反应气隙磁场波形,如图5(a)所示。将图5(a)交轴电枢反应气隙磁场波形进行谐波FFT分解,如图5(b)所示。提取图5(b)交轴电枢反应气隙基波磁密求取
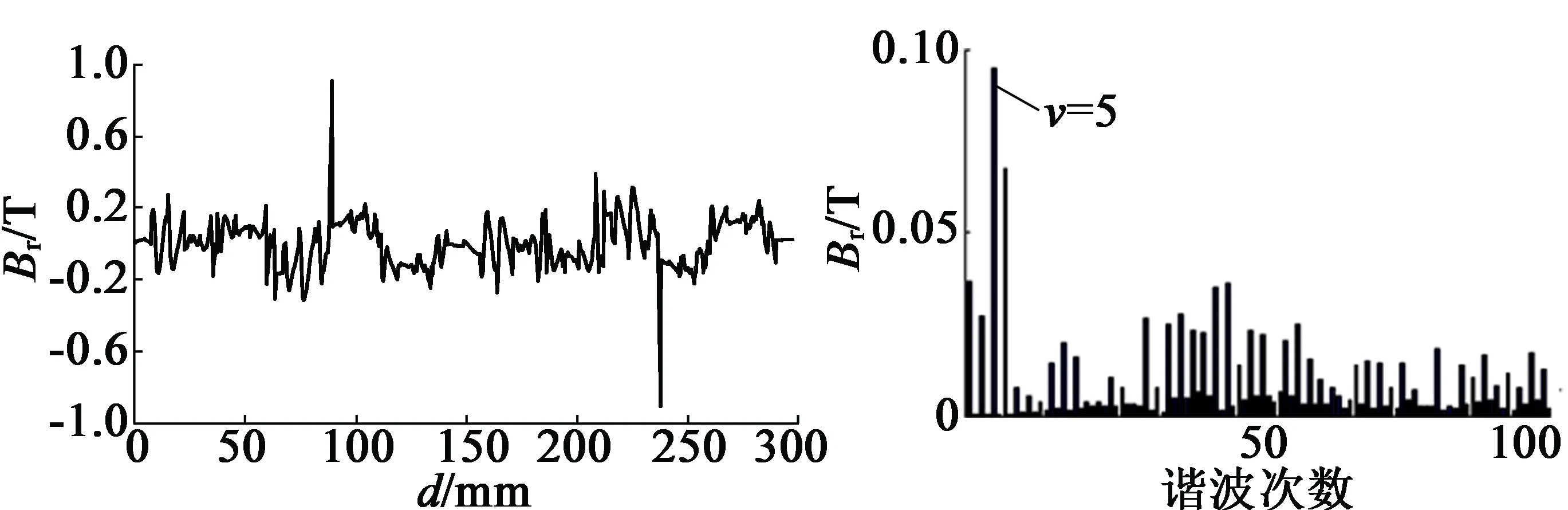
(a) 气隙磁场波形 (b) FFT分解
Eaq。最后,根据永磁电机的矢量分布图计算Lad和Laq,如下式:
(19)
(20)
经计算Lad和Laq分别为1.618 mH和1.539 mH。为获取定子漏感Lν+Ls,需通过前文有限元计算的Ld与Lad作差可以得到Lν+Ls=9.258mH。对于Lν和Ls的分离,结合表2中的Lad+Lν,与有限元计算得到的Lad作差即为Lν=1.816mH,而Ls的获取可以通过Lν+Ls与Lν作差得到,且Ls=7.442 mH。因此,从定子漏感的计算结果看出,分数槽集中式双层绕组的定子漏感远大于电枢反应电感。
根据22 kW 30极36槽双层永磁电机的电感计算方法,可以计算出其单层绕组的d轴和q轴同步电感Ld和Lq分别为14.410 mH和14.091 mH,且与双层绕组同步电感比值为1.32。将有限元方法计算出的单层绕组的Ld与表2中解析计算的Ld相比较可知,有限元计算的同步电感也偏小,且误差为-7.1%(原因同双层同步电感误差分析)。另外,有限元计算的Lad和Laq分别为1.737 mH和1.655 mH,且定子漏感Lν+Ls=12.673 mH。经计算分离出的Lν和Ls分别为4.682 mH和7.991 mH。由此看出,分数槽集中式单层绕组的永磁电机,其定子槽漏感与双层的定子槽漏感近似,而谐波漏感相比于双层的谐波漏感偏大。
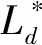
表3 分数槽集中绕组永磁电机同步电感计算值
3 样机计算值与测试值对比
通过上述三台表贴式永磁电机不同极槽配合下直、交轴同步电感的电磁场计算,得出单、双层绕组同步电感的比值变化规律,为验证其合理性及准确性,本文对三台样机采用伏安法测试。表4为计算值与测试值对比结果,且以标幺值表示,其误差对比以实验测试值作为基值,且误差在10%以内,满足电机性能分析和实践应用的需求,证明本文所提方法的正确性。

表4 电感计算值与测试值对比
4 结 语
本文对Q=2p±2的分数槽集中绕组永磁同步电机自感、槽漏感进行了解析研究,并利用电磁场分析和实验测试进行验证,得出以下结论:
1) 分数槽集中绕组永磁电机当Q=2p±2时,自感、槽漏感的解析表达式具有一定的普遍性。同时,可作为伺服驱动系统参数匹配和性能优化参考依据。
2) 对于Q=2p±2的分数槽永磁电机,其单、双层自感比值在1.8~2之间,且单层谐波漏感与自感比值较双层谐波漏感与自感比值偏大,如30极36槽的单、双层谐波漏感占比分别为72.9%和52.9%。另外,当定子槽数相同时,Q=2p+2的自感小于Q=2p-2的自感。
3) 当Q=2p±2时,单、双层每相槽漏感比值在1~1.3之间变化,并随着Q增大,每相槽漏感比值减小。另外,槽漏感对电机性能有较大影响,其数值计算可根据本文的方法进行验算校核。
4) 对于Q=2p±2的表贴式永磁电机,其单、双层绕组同步电感比值除4极6槽和8极6槽外,其余同步电感比值均在1.3~1.4之间。

