基于随机高频信号注入的PMSM无传感器控制
樊温新,杨建飞,2,邱 鑫,2,窦一平,王志伟,王日茗,吕 润
(1.南京师范大学 电气与自动化工程学院,南京 210046;2.南京智能高端装备产业研究院有限公司,南京 210042;3.国电南瑞南京控制系统有限公司,南京 211106)
0 引 言
近年来,永磁同步电动机(以下简称PMSM)效率高、可靠性好、体积小、结构紧凑、对环境的适应性强,已广泛用于家用电器、电梯、电动汽车等行业。在高性能驱动系统中,PMSM的现代矢量控制越来越引起人们的关注[1-2]。转子位置信息的获取通常需要机械传感器,这可能会导致一些问题[3],如高成本、降低系统的可靠性和较差的环境适应性,尤其是在低速或零速范围内范围。许多学者已经广泛研究了基于高频信号注入的PMSM无传感器控制,然而这些方法的主要问题之一是会带来额外的噪声,导致严重的噪声污染[4]。学者们为减少与注入高频信号密切相关的噪声做出了巨大的努力,通过减小信号幅度来降低噪声。例如,Medjmadj S等学者已经使用现场可编程门阵列(FPGA)来处理数据,以最大程度地提高A / D转换率,并使用电流过采样方法来最小化注入信号的幅度[5]。另一种选择是频率调整策略,通过该策略信号频率可以增加到人耳无法听到的水平[6],或降低到人耳可以接受的更柔和的水平[7]。
通常,高频信号注入会伴有噪声,因此减少这种负面噪声影响非常重要。本文研究了一种基于随机高频信号注入(RFSI)的PMSM无传感器控制方法。首先,建立信号处理的分析模型;通过使用该模型,可通过MATLAB/Simulink构建控制系统。仿真结果表明,该方法简单易用,可以有效降低噪声。
1 信号处理分析模型
1.1 PMSM数学模型
PMSM在d,q同步坐标轴中的数学模型可以表示:
(1)
式中:ud,uq,id,iq,Rd,Rq,Ld和Lq分别是定子电压,定子电流,定子电阻和定子电感;ωe是转子电角速度;ψf是永磁通量;s是Laplacian运算符。
对于零速或低速,可以忽略式(1)中与速度有关的项ωeψf,ωeLd和ωeLq,可以获得:
(2)
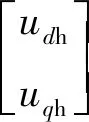
(3)
式中:下标“ h”代表“高频”。
1.2 信号处理方法
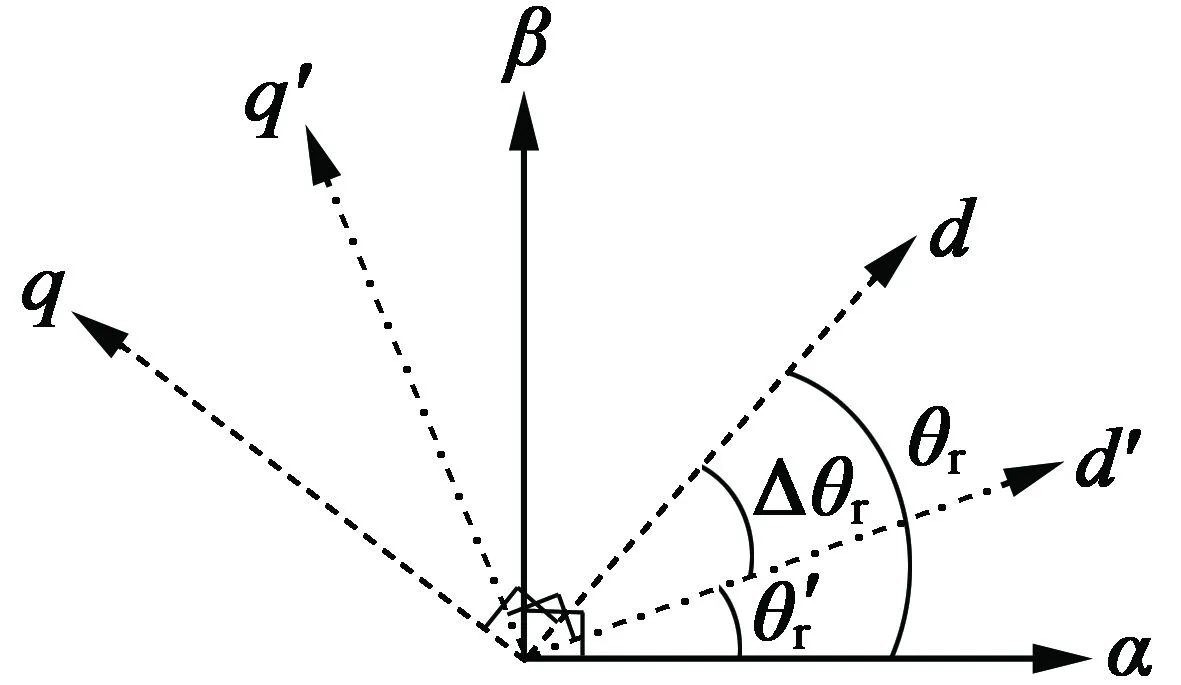
图1 各坐标系间关系示意图
不同坐标系之间的变换关系如下:
(4)
(5)
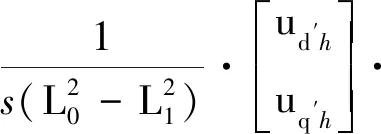
(6)

当将高频电压信号uinj注入到d′轴时,由高频信号引起的电流响应高频分量:
(7)
(8)
如果位置估计误差Δθr足够小,则可以得到sin(2Δθr)=Δθr,sin(Δθr)≈0和cos(Δθr)=1。因此,可以导出:
(9)
(10)
为了获得位置信息,需要与注入信号有关的解调系数kd。在高频电压信号注入法中,可以将注入信号设置uinj=Vinsin(ωint),并且解调系数kd=sin(ω0t+b0),并且将经过高通滤波器处理的iαh乘以kd,得到如下式:
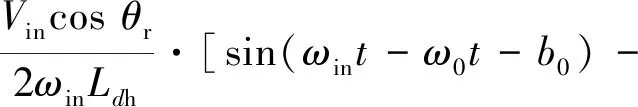
sin(ωint+ω0t+b0)]=Kdcosθr
(11)
式中:Kd是与转子位置无关的变量。
为了消除电机参数的影响,通常需要进行归一化处理,这意味着变量Kd始终应该大于零。如果kd=-cos(ωint),那么:
(12)
通过低通滤波器后,解调信号变为下式:
iαθ=LPF(iαhkd)=Kθcosθr
(13)
式中:Kθ大于零且与转子位置无关;iαθ是经过LPF之后的解调信号;LPF是低通滤波器。
归一化过程如下式:
(14)

(15)
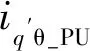
2 随机高频信号注入策略
2.1 随机高频信号注入方法
频谱分析表明,对于固定频率信号注入方法,功率谱密度波形在频率f0会出现一个高峰值。 注入信号的频率通常在人耳的听觉范围内(20 Hz~20 kHz),因此它将产生更尖锐的听觉噪声,注入信号的幅频比越大,噪声就越高。为了减少高频噪声,随机高频信号注入(以下简称RFSI)方法是一种有效的选择,通过该方法可以将两个不同频率的高频正弦电压信号以随机方式异步注入到电动机中。RFSI电路的结构框图如图2所示。
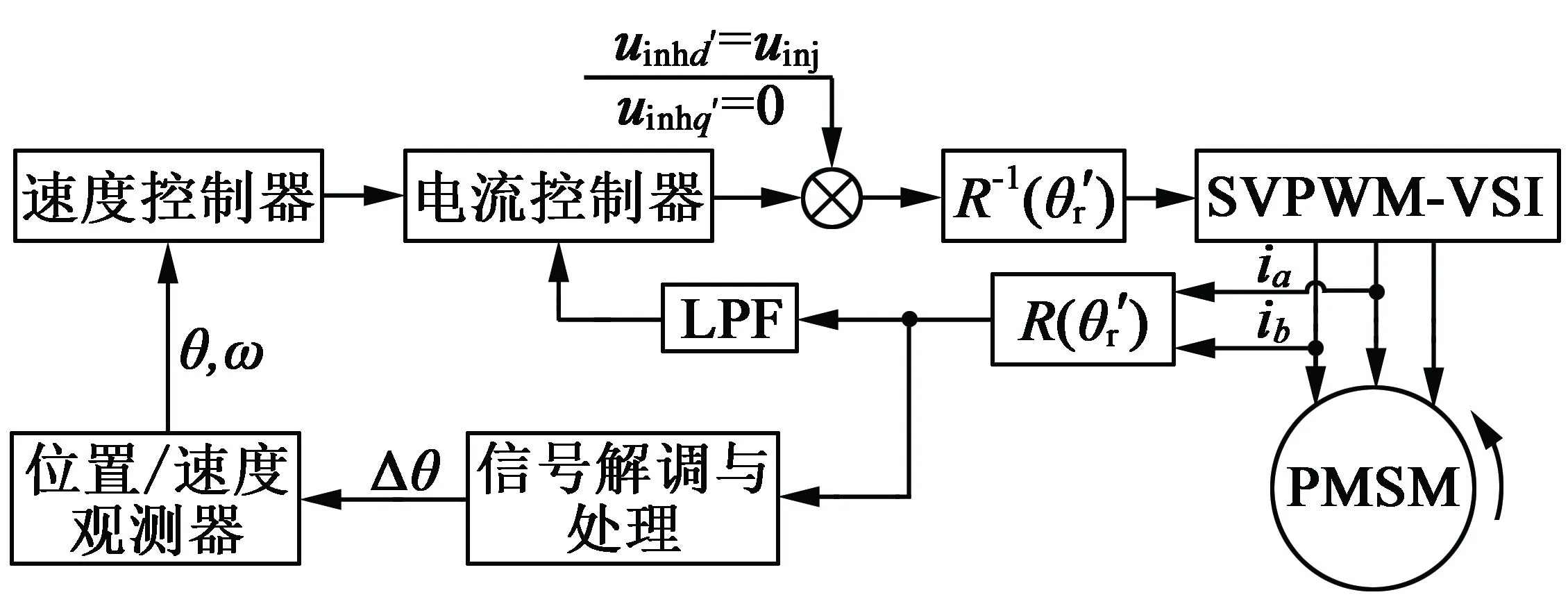
图2 随机高频信号注入法结构框图
2.2 随机高频信号的选择
2.2.1 随机高频信号的频率
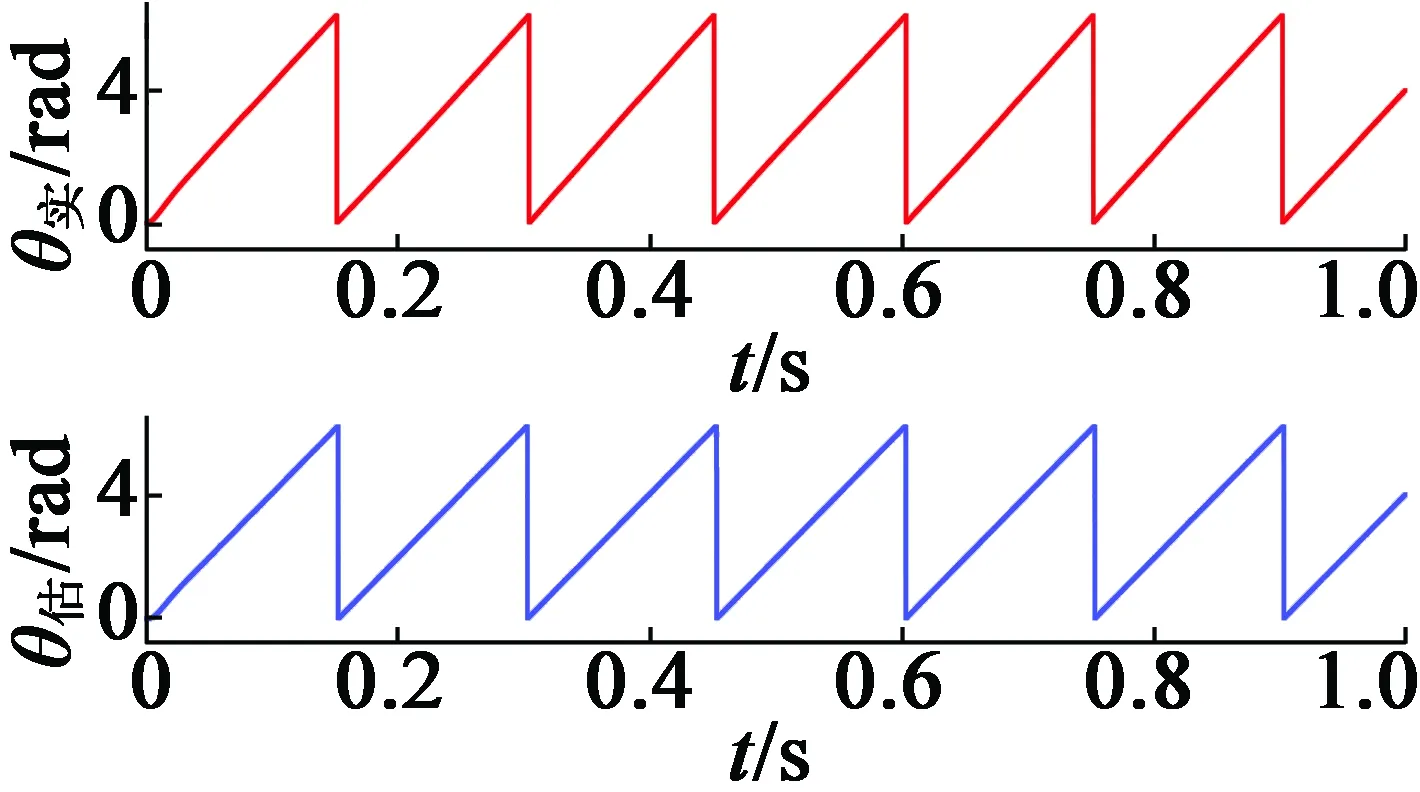
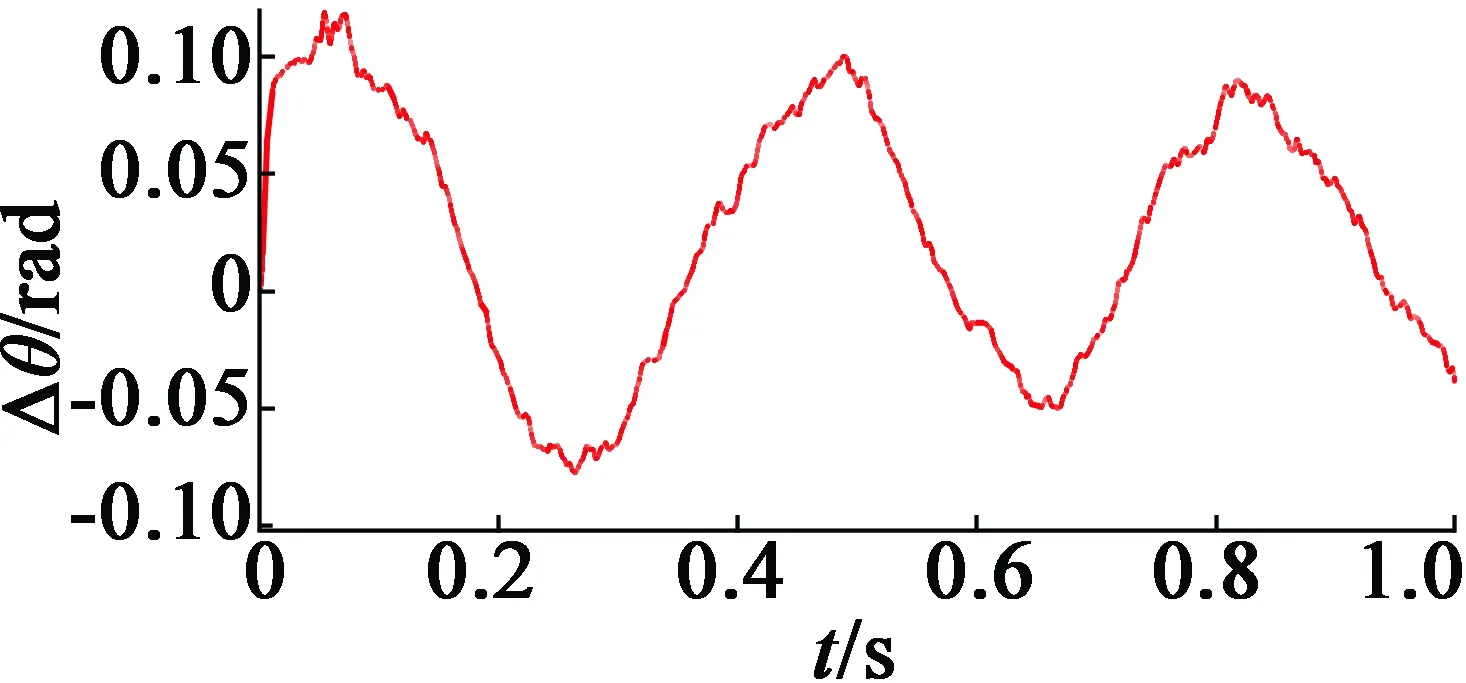
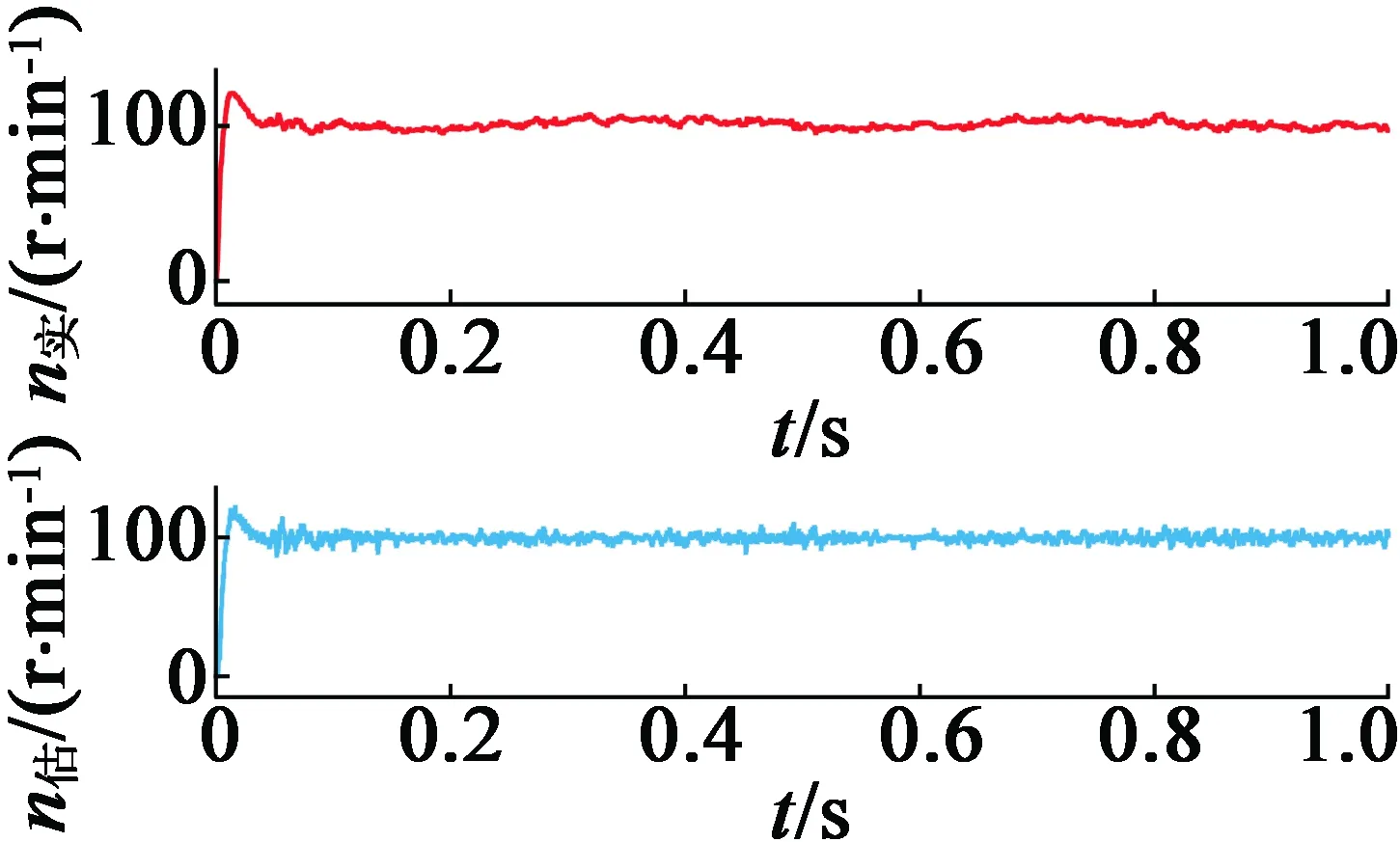
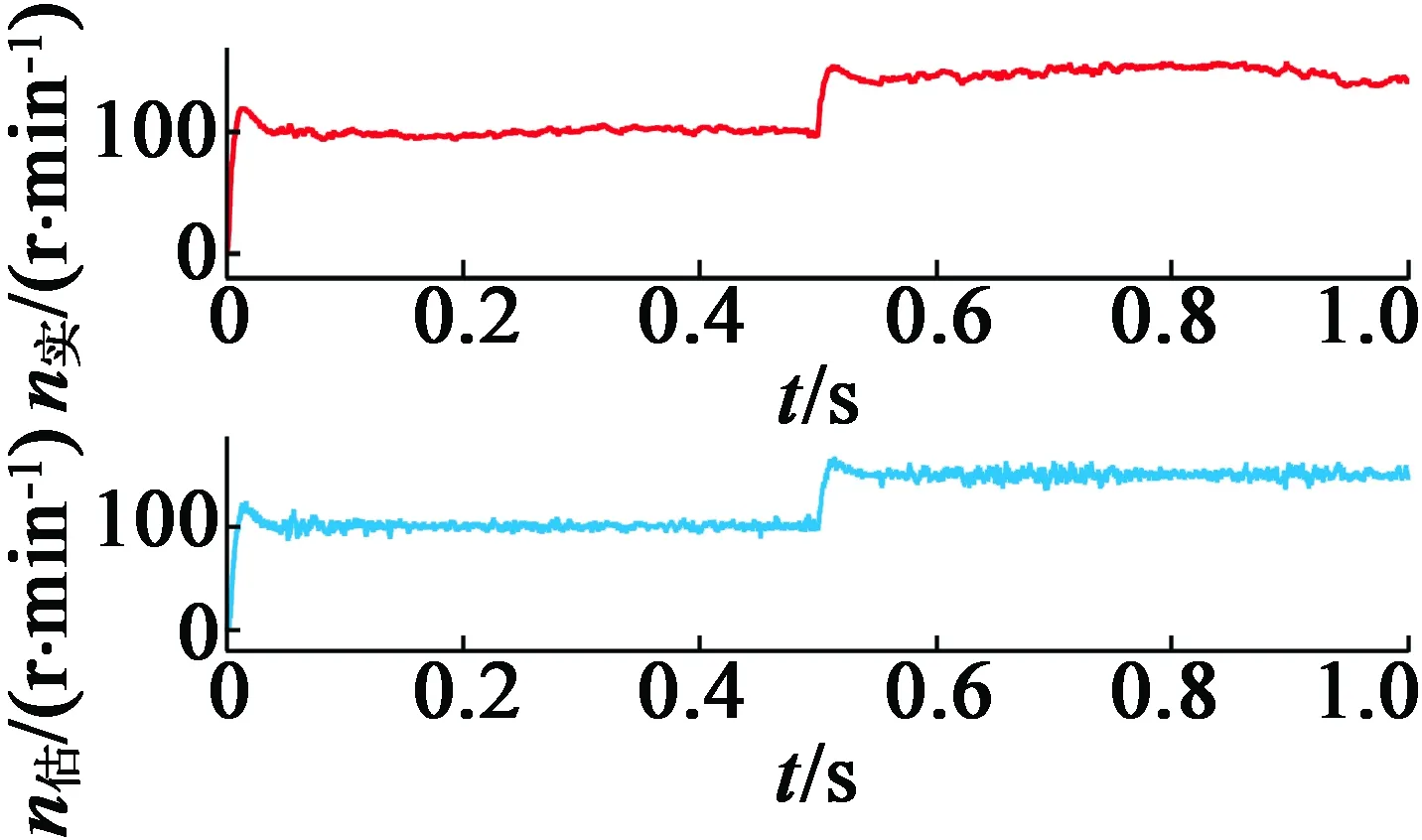
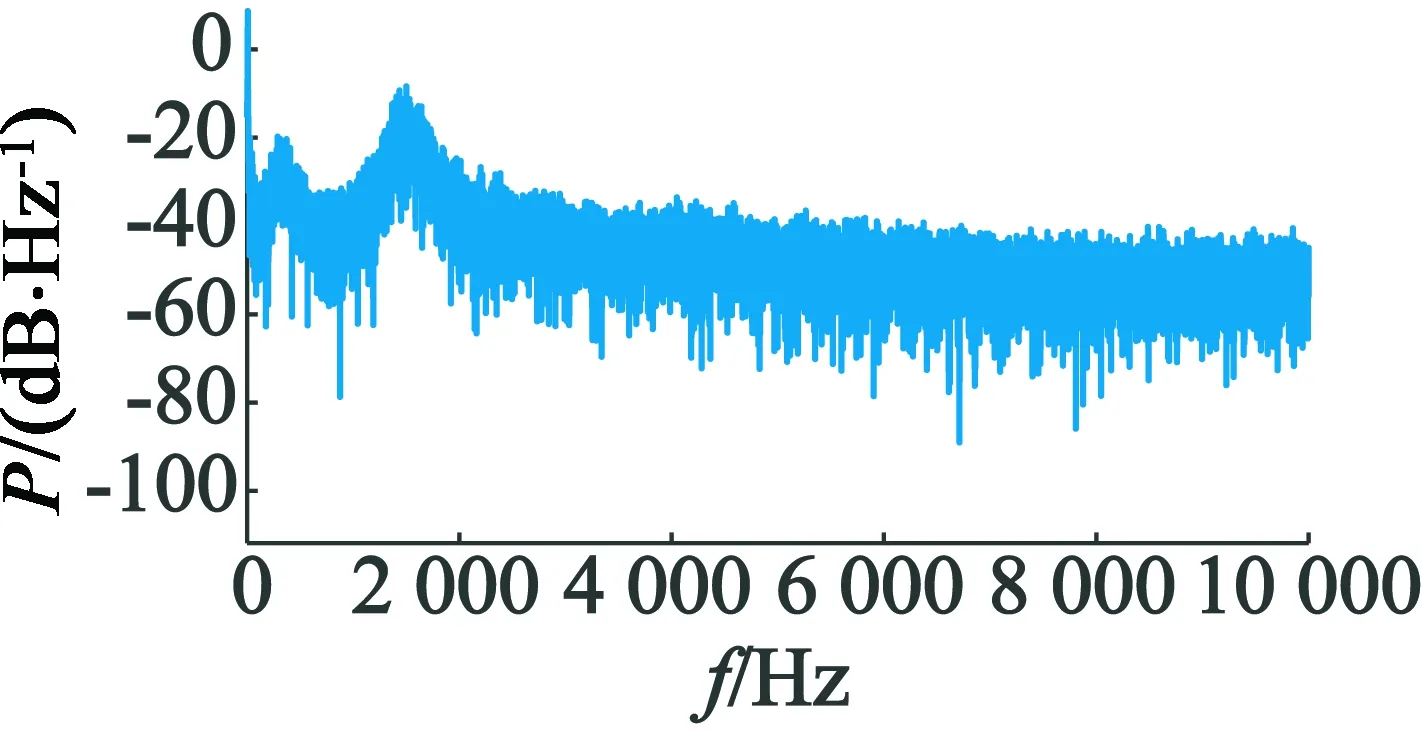
首先,由于高频电压信号通过逆变器注入到电动机绕组中,因此注入信号的周期必须是PWM周期Ts的整数倍。逆变器的PWM载波频率fs=6 kHz,选择两个正弦波信号u1=V1sin(ω1t)和u2=V2·sin(ω2t),其频率分别为f1=fs/n1和f2=fs/n2,其中n1 另外,为了确保估计精度,低频f2不能太小。u1的发生概率为P,则u2的发生概率为1-P。确定两个信号后,通过更改P将功率谱调整为平坦。 2.2.2 随机高频信号的幅值 为了在改变注入信号时减少谐波,需要调整高频信号的幅度及其频率,以保持电流幅度恒定。从式(12)可以看出,要使Kd中的直接分量恒定,这意味Vin/(2ωinLdh)应该是恒定的,高频信号Vin的幅值必须与其角频率ωin成比例,即V1/f1=V2/f2。 为了生成随机高频信号,首先选择具有不同频率的两个信号作为基本注入信号,然后利用程序生成随机码产生随机数R,在注入周期开始时,将R与设定的信号切换概率P进行比较,如果R 为了验证RFSI方法,选择一个典型PMSM,并构建了一个RFSI电路,如图2所示,以通过MATLAB/Simulink进行仿真。表1列出了PMSM的主要参数。 表1 电机参数 以下研究了不同频率和概率的仿真。例如,考虑到正弦波的完整性和降噪效果,将两个注入信号设置为1 kHz/135 V和1.5 kHz/202 V,每个信号的概率为50%。以给定速度100 r/min进行恒定负载转矩为5 N·m的模拟仿真。高频电流信号及其放大图如图3和4所示,可以看出,电流中叠加高频分量,且高频分量的频率发生了变化。 图3 α,β静止坐标系中高频电流的仿真结果 图4 α,β静止坐标系中高频电流的仿真结果放大图 稳态性能测试的仿真是在负载恒定为5 N·m的情况下以速度100 r/min进行的。仿真结果如图5~图8所示。 图5 转子位置估计值与实际值的变化曲线 图6 转子位置估计误差的变化曲线 图7 转速估计值与实际值的变化曲线 图8 转速估计误差的变化曲线 从以上结果可以看出,RFSI方法有效地控制了电动机的稳态运行,实际曲线与估算曲线之间具有良好的一致性。 对于转子位置、最大估计误差小于0.125 rad;对于速度、最大估计误差小于13 r/min。 如图9所示(负载为5 N·m),系统的动态特性也已经过测试,结果表明,实际曲线和估计曲线之间有较好的一致性。 图9 动态速度曲线从100~150 r/min 为了评估降噪效果,分析并比较了不同控制方法之间的相电流功率谱。不同方法的功率谱密度曲线如图10所示。 (a) 1 kHz 信号注入 (b) 1.5 kHz 信号注入 (c) 随机信号注入(1 kHz和1.5 kHz) 从图10可以看出,与固定频率信号注入方法相比,RFSI方法可以显著降低功率谱密度波形的峰值,这意味着可以有效地降低噪声。 本文研究了一种用于PMSM的无传感器RFSI控制方法。通过采用这种方法,与传统的固定频率信号注入相比,可以提高系统在稳态和动态状态下的性能。建立了信号处理的计算模型,并通过MATLAB/Simulink建立了RFSI电路仿真模型。仿真结果表明,对于稳态运行,转子位置和速度的实际和估算曲线相吻合,转子位置的最大估算误差小于0.125 rad,转速的最大估算误差小于13 r/min。不同控制方法的功率谱曲线比较表明,RFSI方法可以更有效地降低噪声。2.3 随机高频信号的产生和解调系数
3 仿真结果






4 结 语

