月壤样品袋整形缠绕运动分析与仿真
国树东, 王 刚, 齐朝晖*, 张欣刚, 魏 妹
(1.大连理工大学 工业装备结构分析国家重点实验室,大连 116024;2.大连理工大学 海洋科学与技术学院,盘锦 124221); 3.青岛理工大学 理学院,青岛 266520)
1 引 言
月球探测是深空探测的基础,对于提高人类对宇宙的认识,推动科技和经济发展具有重要的意义[1,2]。目前,我国正在实施探月三期工程,目标是采集深度约2 m并保持层序信息的月壤样品[3,4]。
月壤样品钻取完成后,将采样样品收集于样品袋内,然后整形缠绕在回转卷筒上等待回收[5-8]。由于样品袋为柔性结构,在整形过程中极易发生重叠和滑落等现象,为了确定顺利缠绕的条件,需要对样品袋缠绕过程进行运动学建模和受力分析。
由于技术保密等原因,可参考的资料相对较少。刘天喜等[9,10]采用离散元法对整形过程中样品袋内的月壤进行了力学分析,为钻取机构设计提供了理论指导。但却无法模拟样品袋整形的整体运动过程,无法计算整形机构参数与各力学参量之间的关系。由于月壤颗粒数量庞大,还会出现计算量过大和计算时间较长等问题。
整形缠绕系统中,与卷筒接触的样品袋受到的是形状约束。学者们对形状约束问题做了大量研究,Hong等[11]为研究物体在一维介质中的运动提出了任意欧拉-拉格朗日绝对节点坐标单元(ALE-ANCF),解除了单元节点与物质点的绑定,并在求解一些工程问题中得到了应用。Fu等[12]提出了一种多尺度索轮系统建模方法,索与轮非接触部分采用ALE单元建模,接触部分作为约束该单元的边界条件。齐朝晖等[13]提出了一种单元节点既不与空间坐标固定也不与物质坐标固定的动态节点绳索单元,精细描述了滑轮绳索的运动,简化了分析过程。这些研究工作充分说明了采用单元节点与物质点解除绑定的空间描述法解决带形状约束问题的必要性和可能性,对样品袋缠绕过程的运动学分析具有重要的指导意义。
本文基于空间描述法建立月壤样品袋整形缠绕系统的运动学模型,以期揭示系统部件物理量间的关系,得到影响整形的关键因素和样品袋顺利缠绕的卷筒驱动条件,对系统的设计提供理论参考。
2 整形缠绕系统运动学模型
2.1 整形缠绕系统
整形缠绕系统主要包括回转卷筒驱动部分和导向套轴向进给部分,如图1所示。在卷筒驱动下,样品袋前端的拉绳被缠绕在卷筒上,从而将样品袋提升至卷筒端口处,然后通过导向套引导,使其沿卷筒轴向自上而下逐渐缠绕到卷筒上。
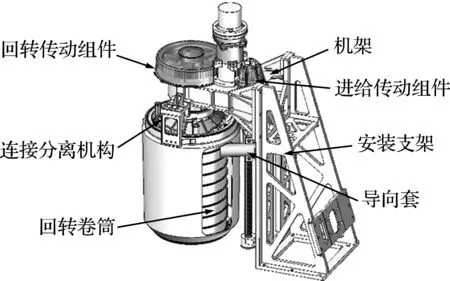
图1 月壤样品袋整形缠绕系统
整形缠绕分析过程是从样品袋一端刚进入卷筒开始直到全部缠绕在卷筒上结束,模型如图2所示。系统中起支撑作用的结构等效为样品袋所受的支撑力和摩擦力。由于样品袋弹性伸缩率较低,故整形过程中忽略其轴向伸长,并假设样品袋截面保持不变。
为了便于分析,对样品袋初始状态作标记,A为缠绕起点,AB为卷筒和导向套间无支撑约束段,BC和CD为受导向套约束的直线和圆弧段,DE为导向套和导轨间无约束过渡段,EF为受导轨约束倾斜段,FG为导轨末端圆弧段,GH为无约束竖直段。
2.2 整形缠绕系统运动方程
以卷筒底面中心点为原点建立坐标系,如图2所示。系统中标记点弧长坐标随时间的变化规律均可由卷筒入绳点的描述变量表示,因此选取卷筒入绳点处样品袋的弧长坐标s0、纵向坐标z0和样品袋水平倾角θ0作为系统描述变量。
卷筒入绳点和导向套出口B的矢径分别为
r0=z0ez,r1=z1ez+δex
(1,2)
式中z1为B点纵向坐标,δ为AB间水平距离。
卷筒入绳点的空间速度为
(3)
样品袋水平倾角满足
tanθ0=δ-1(z0-z1)
(4)
卷筒入绳点的物质速度为[13]
(5)
式中∂r0/∂s=cosθ0ex-sinθ0ez。
卷筒入绳点处卷筒上的物质速度为
(6)
式中r为卷筒与样品袋半径之和,ω为卷筒角速度。
理想状态下,样品袋随卷筒同步运动,即卷筒入绳点物质速度与卷筒上相应点物质速度相等,则
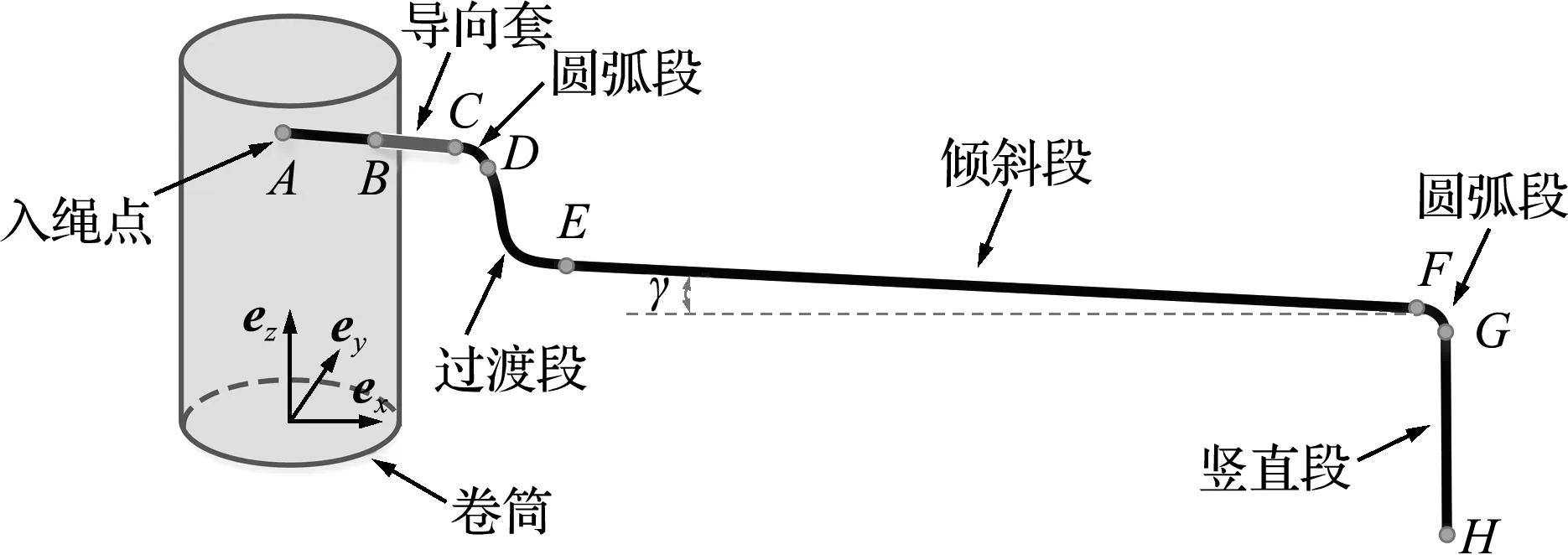
图2 月壤样品袋整形缠绕系统运动学模型
reshaping and winding system
(7)
由式(3,7),可得
(8,9)
对式(4)求时间导数
(10)
导向套以速度vd匀速向下运动,则有
z1=h-vdt
(11)
式中h为卷筒高度。
此时,卷筒入绳点纵向坐标满足方程
(12)
由于在初始时刻z0=h,方程(12)的解为
z0=h-vdt+vdδ(1-e-ω r t /δ)/ωr
(13)
因此,水平倾角满足如下变化规律。
tanθ0= (ωr)-1vd(1-e- ω r t/δ)
(14)
由式(14),样品袋整形不久,倾角将稳定在
(15)
导向套运行速度计算公式为
(16)
式中d为样品袋直径。
由式(15,16)可知,导向套运行速度需满足
(17)
由式(8,14)得弧长坐标变化率为
(18)
至此,得到整形缠绕系统卷筒入绳点处样品袋的系统运动方程。
2.3 样品袋过渡段弧长求解
为了分析样品袋运动规律,需要得到整形过程中其末端的点所处的位置,因此要计算样品袋待卷入卷筒的弧长。样品袋圆弧段、倾斜段和竖直段弧长容易准确计算,难点在于过渡段弧长的求解。
一般样条插值或Hermite插值对小曲率曲线弧长的求解比较准确,对大曲率的曲线则存在较大误差,而样品袋过渡段属于大曲率曲线,为了得到更加准确的弧长,采用累加弦长插值法[14]。
选取过渡段两端点间弦长λ作为描述参数,端点处λ1= 0,λ2=‖r2-r1‖,端点切向量取单位向量[14]。
插值曲线为
(19)
形函数为
(20)
(21)
(22)
(23)
曲线对弦长的导数为
(24)
整理可得,过渡段曲线弧长为
(25)
式中xi和wi为高斯积分点和权量系数。
3 样品袋顺利缠绕受力分析
3.1 卷筒驱动条件
卷筒入绳点处样品袋拉力可以描述为
TA=TAgs
(26)
式中gs和TA为入绳点处样品袋切向矢量和拉力值。
卷筒入绳点处样品袋受力如图3所示。样品袋与卷筒间的接触力可以表示为
T=N1en+N2ez
(27)
式中en为卷筒外法向矢量。
样品袋上一点的加速度为
a=-ω2ren
(28)
将卷筒入绳点视为一微元体,列平衡方程为
(29)

(30)
则样品袋与卷筒间法向和径向接触力分别为
(31)
(32)
满足样品袋顺利缠绕的卷筒驱动条件是,既要保证样品袋与卷筒表面接触,又要保证样品袋不从卷筒上滑落,即N1> 0,μN1>N2> 0。
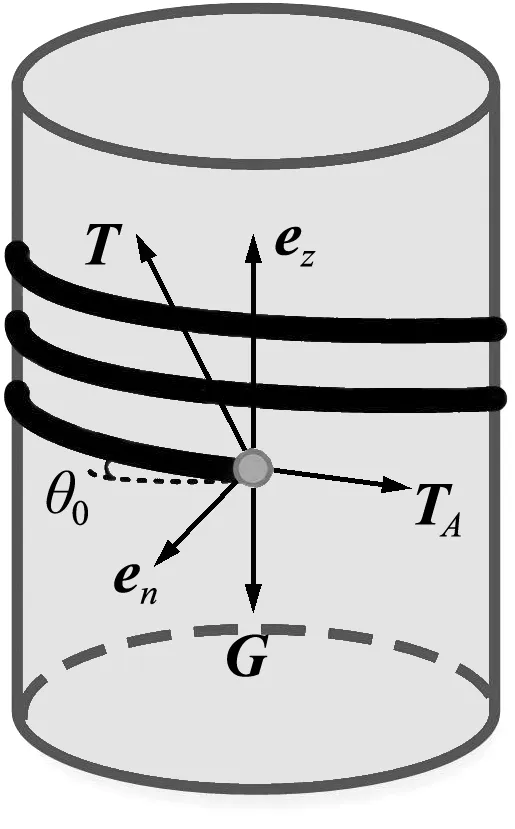
图3 受力分析
3.2 样品袋受力分析
样品袋标记点的受力影响到卷筒入绳点处拉力和样品袋整形缠绕,因此需要对其进行分段受力分析,如图4所示。
(1) 圆弧段受力分析
对圆弧段上一微元体,列平衡方程
(33)
式中es和en为微元体处切向和法向矢量,r1为圆弧半径,fa为合外力,v为线速度。
CD和FG为圆弧段,以FG为例,整理可得
TF=ρv2+ (TG-ρv2)eμ (φ - φ0)+α1eμ (φ - φ0)-αt
(34)
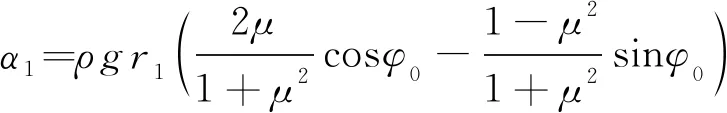
(2) 过渡段受力分析
为了减少求解误差,采用虚功率原理求解DE两端的拉力[15],虚功率方程为
(35)
式中s-1和s1为标准区间[-1,1]起止弧长。
整理可得
(36)
当样品袋从导轨脱离后,样品袋形状近似不变,切向物质加速度为0,可得
TD=TE+ρg· (rE-rD)
(37)
(3) 直线段受力分析
G点受力由竖直段样品袋重力决定,则
TG=ρg(sH-sG)
(38)
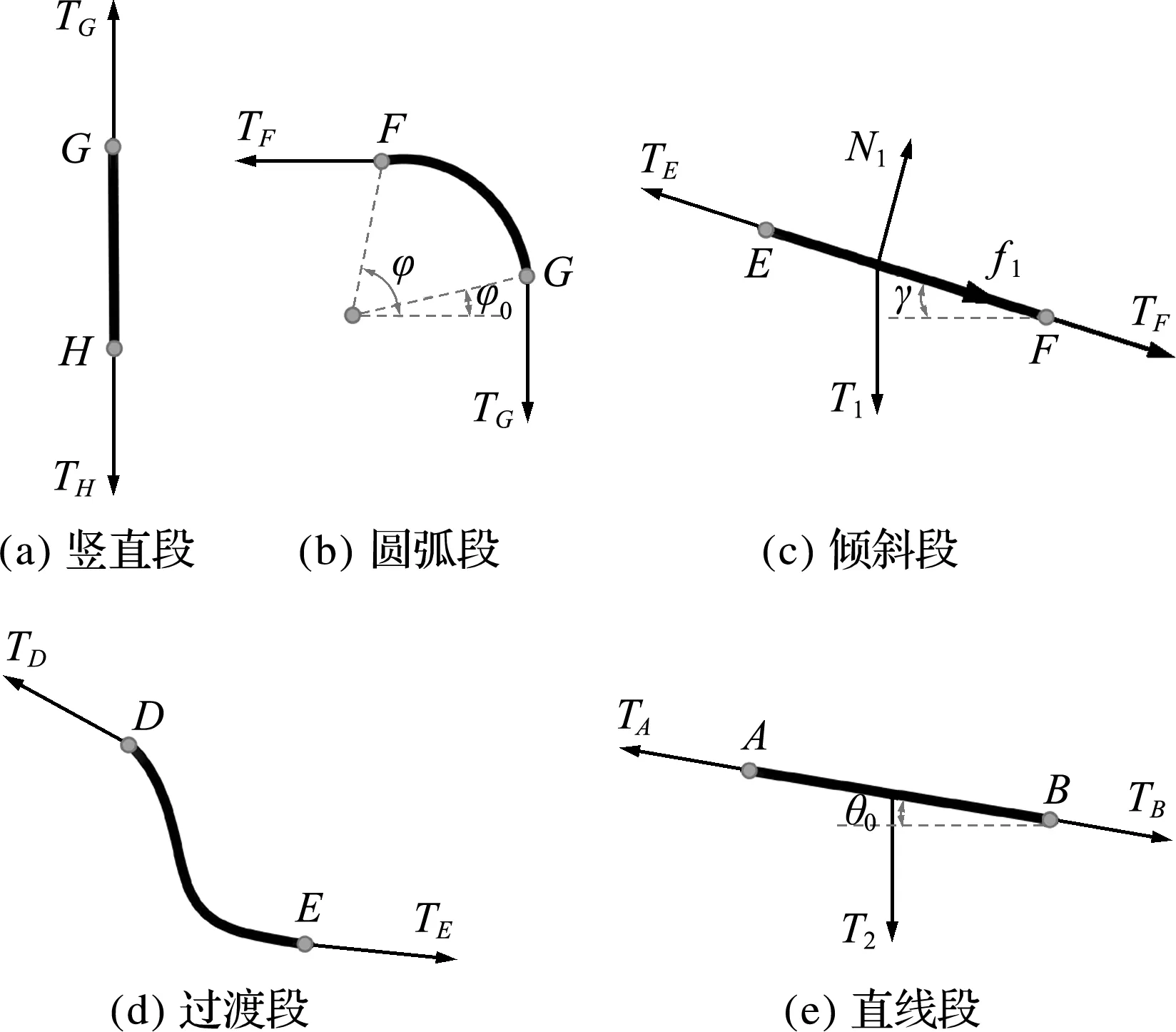
图4 月壤样品袋标记点受力分析
CD和EF为直线段,以EF段为例,整理可得
TE=TF+μT1cosγ+T1sinγ
(39)
式中T1=ρ(sF-sE)g,γ为导轨与水平面夹角。
AB距离极短,可视为直线,虚功率方程为
(40)
整理可得
TA=TB+ρg(sB-s0)sinθ0
(41)
式中ρ为样品袋线密度,θ0为AB与水平轴的夹角。
4 数值算例
对整形缠绕系统进行仿真,相关参数如下。月球重力加速度为1.633 m/s2,月壤密度为1580 kg/m3,样品袋与卷筒、导向套和导轨间摩擦系数均为0.2,卷筒角速度为0.6 r/min,卷筒直径为112.2 mm,卷筒高度为110 mm,样品袋长度为2000 mm,样品袋直径为17 mm,导轨长度为1300 mm,导轨水平倾角为8.5°,导轨末端到卷筒入绳点间距为170 mm,导向套运行速度为11.63 mm/min,导向套水平长度为100 mm,导向套末端到卷筒入绳点距离为50 mm。
4.1 工况1
按照默认参数,样品袋重叠(样品袋不同圈发生重合叠加的现象)缠绕点计算结果如图5所示。可以看出,样品袋重叠缠绕点仅出现在第一圈和第二圈的起始点处,其他位置缠绕情况良好。
样品袋缠绕失效点(样品袋与卷筒脱离接触或滑落处)如图6所示。可以看出,在缠绕到第五圈时,样品袋拉力不足以使其缠绕在卷筒上,样品袋从卷筒上脱离接触和滑落,滑落失效起止角度为266.0°和331.6°,滑落失效长度为73.93 mm;接触失效点位于最末端处。
卷筒阻力矩由卷筒转动惯量和样品袋拉力引起,如图7所示。可以看出,阻力矩整体数值相对较小,最大值为207.2 N·mm;随着样品袋不断缠绕呈现逐渐减小趋势,在0.9750 min后变化趋缓,这是由于0.9750 min之前样品袋竖直段处在逐渐提升状态,卷筒所受阻力矩较大,下降较快,至 0.9750 min 时,样品袋完全提升至导轨上,卷筒阻力矩随后逐渐减小,下降速度较慢。

图5 样品袋重叠缠绕点
4.2 工况2
通过仿真发现,系统对导向套运行速度比较敏感。调整导向套运行速度为12.83 mm/min,样品袋重叠缠绕点如图8所示。可以看出,样品袋重叠缠绕点出现在第四圈和第五圈末端,重叠角度为86.70°,重叠长度为97.70 mm。
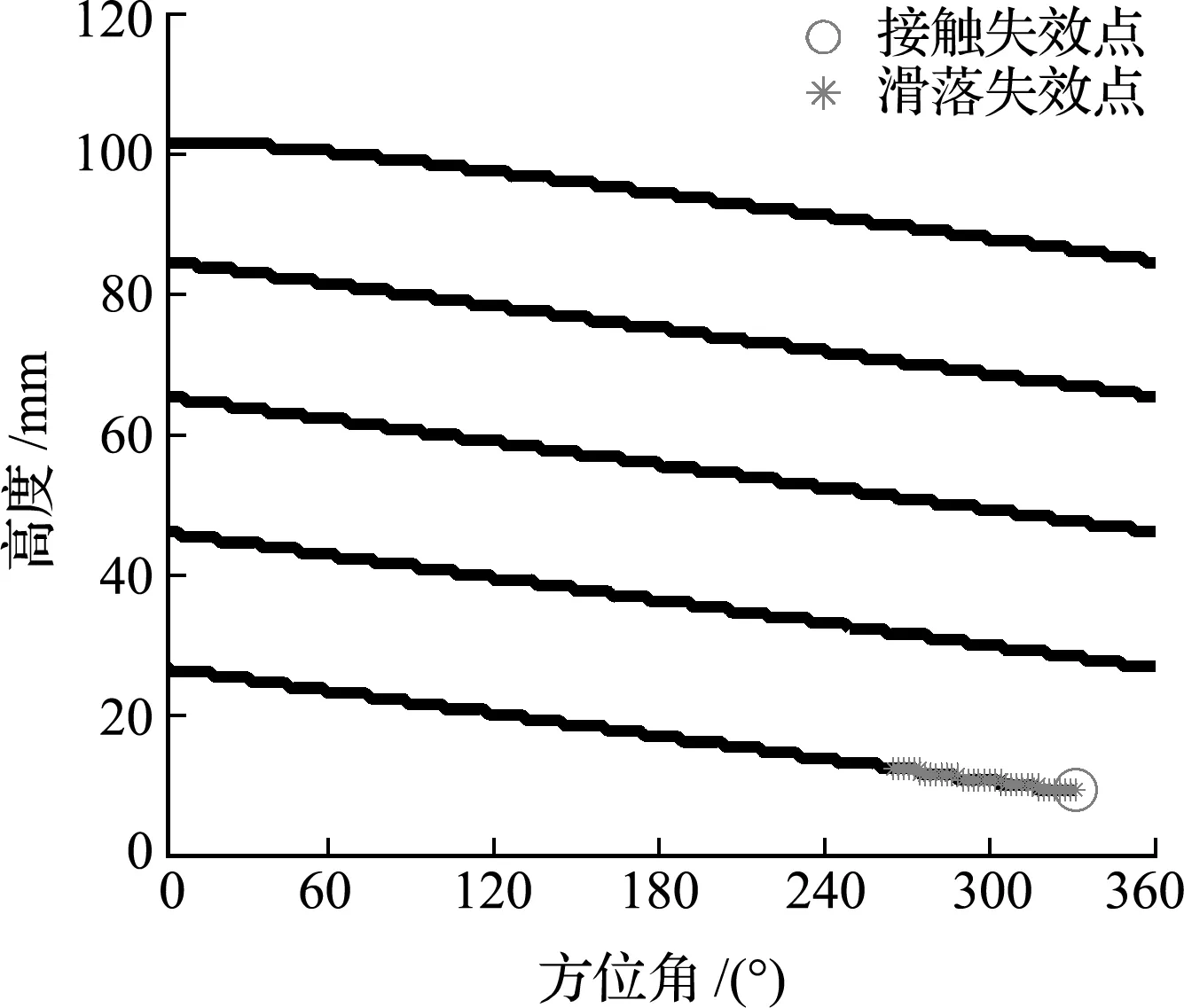
图6 样品袋缠绕失效点

图7 卷筒所受阻力矩
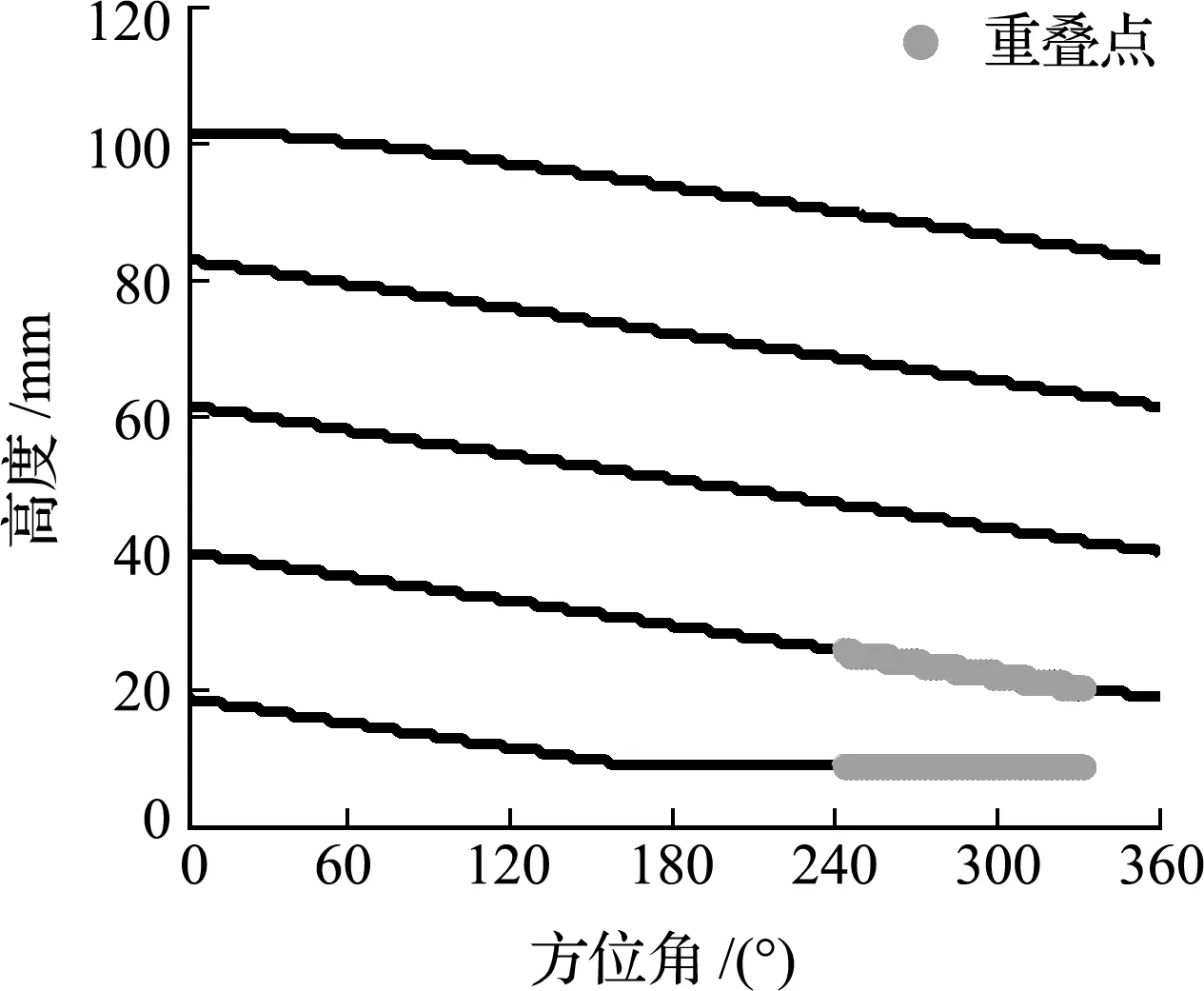
图8 样品袋重叠缠绕点
样品袋缠绕失效点如图9所示。可以看出,样品袋缠绕到第五圈时从卷筒上脱离接触并滑落,滑落失效起止角度为265.7°和331.6°,滑落失效长度为74.26 mm;接触失效点位于最末端处。
卷筒所受阻力矩和工况1变化趋势一致,最大值为207.2 N · mm,在0.9767 min以后变化趋缓;当继续增大导向套运行速度,样品袋重叠长度增大,失效点增多,而卷筒所受阻力矩变化不大。
4.3 工况3
调整导向套运行速度为10.43 mm/min,样品袋重叠缠绕点如图10所示。可以看出,样品袋重叠缠绕点出现在第一圈和第二圈前端,重叠角度为76.00°,重叠长度为85.65 mm。
样品袋缠绕失效点如图11所示。可以看出,样品袋缠绕到第五圈时从卷筒上脱离接触并滑落,滑落失效起止角度为266.0°和331.9°,滑落失效长度为74.26 mm;接触失效点位于最末端处。
卷筒所受阻力矩和工况1变化趋势一致,最大值为207.2 N·mm,在0.9717 min以后变化趋缓;当继续减小导向套运行速度,样品袋重叠长度增大,失效点增多,卷筒所受阻力矩变化不大。
图9 样品袋缠绕失效点
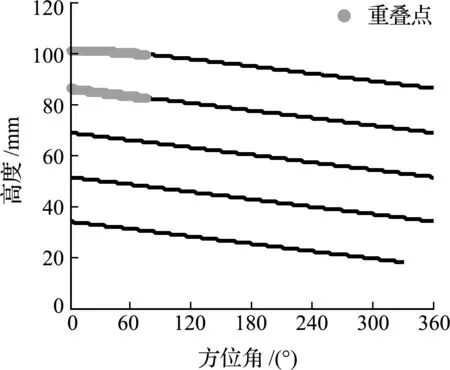
图10 样品袋重叠缠绕点
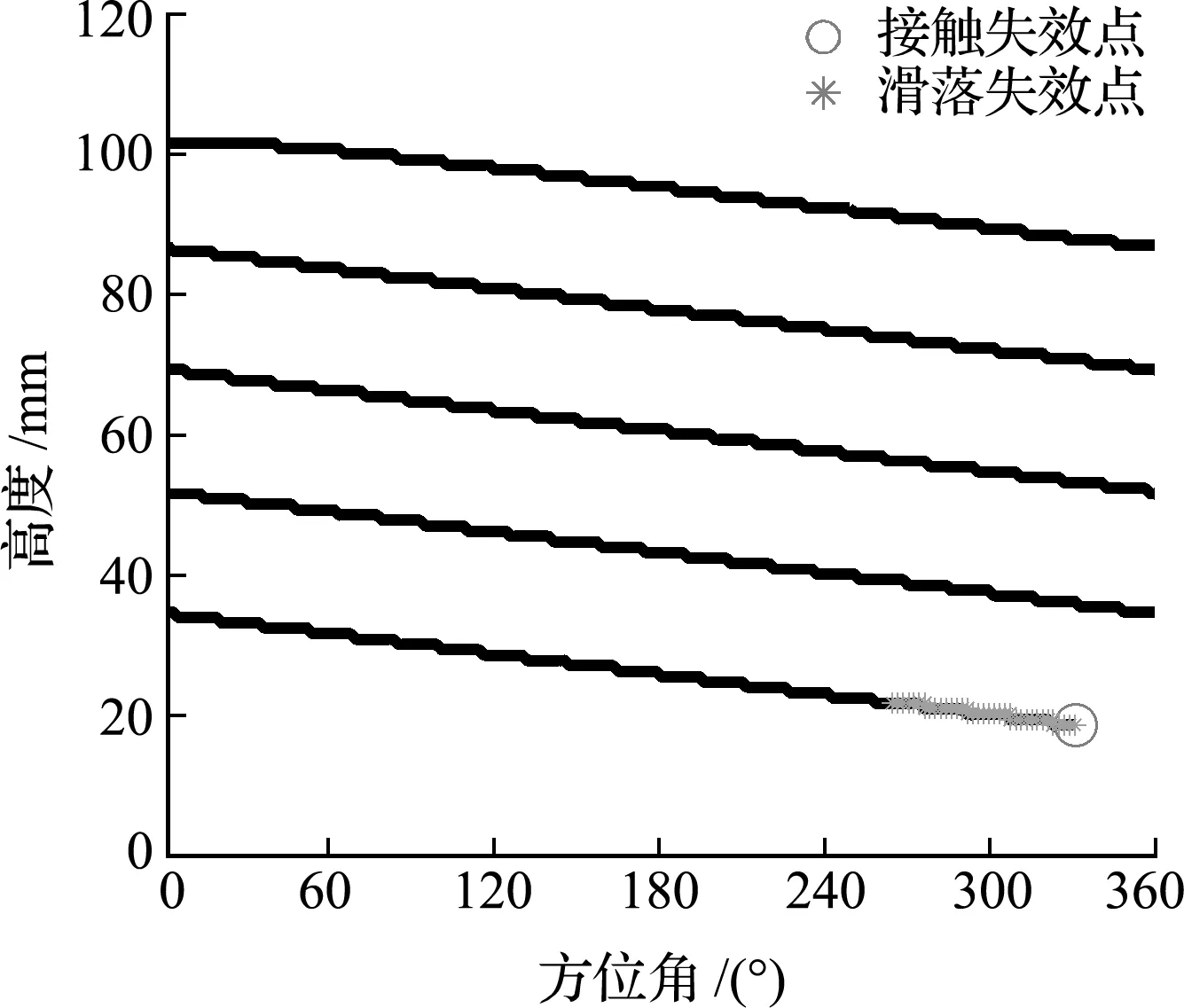
图11 样品袋缠绕失效点
5 结 论
(1) 导向套运行速度是影响月壤样品袋整形缠绕的关键因素,且需要与卷筒角速度匹配调整。当卷筒角速度为0.6 r/min时,导向套运行速度调整为11.63 mm/min,可以使样品袋重叠点和失效范围达到最小。
(2) 月壤样品袋整形缠绕过程中,若样品袋拉力不足,会导致样品袋与卷筒脱离接触或滑落,此时需要提供卷筒轴向托举力等方法保证其正常缠绕。

