谐波型波磨激扰下轮轨系统接触蠕滑特性

王志强， 雷震宇

(1.同济大学 铁道与城市轨道交通研究院,上海 201804；2.上海市轨道交通结构耐久与系统安全重点实验室，上海 201804)

1 引 言

轮轨系统激扰是引起车辆部件振动以及轮轨系统振动的主要原因,产生的高频振动和冲击噪声对车轮和轨道危害极大,同时对车辆运行的平稳和舒适,以及周边环境等都有重要的影响。轮轨系统的激扰由车辆和轨道两方面的因素造成。车辆方面主要是车轮擦伤、偏心和踏面不圆顺等因素,而轨道方面主要是轨道的几何不平顺,包括普遍存在的钢轨波浪型磨耗,以及钢轨接头状态不良和轨下基础缺陷等。

国内外很多学者对这些激扰所引发的轮轨动力作用做过研究,如Mok等[1]运用仿真软件分析了由车轮压扁等缺陷引起的冲击荷载对轨头垂直裂纹传播的影响。Kouroussis等[2]在同时考虑了钢轨不同接头缺陷和车轮踏面擦伤的情况下,分析了轮轨冲击对地面振动水平的影响以及各因素的敏感性。温泽峰等[3]分析了不同轴重和车速对接头处钢轨应力应变分布规律的影响。罗文俊等[4]对无缝线路大于0.3 mm/m焊接接头的垂向轮轨冲击力和钢轨、轨枕振动加速度进行了打磨前后的对比试验测试。宋小林等[5]以实测地铁内轨波磨为激扰,提出了波磨的波深时变率概念,并分析了其与轮轨垂向力和钢轨垂向加速度的对应关系。此外,车轮多边形现象对轮轨动力行为的影响,也是当前铁路领域研究的一大热点问题[6-14]。

综上所述,轮轨系统激扰作用下的轮轨接触问题是研究地铁波磨发生发展机理的重要切入点。本文以钢轨波磨连续谐波激扰为输入,因为谐波激扰对应的动力学响应明确，有利于寻找和发现激扰与响应之间的对应关系，而波磨的周期特性明显，任意周期激扰总可以用谐波形式的傅里叶级数来表示。通过多体动力学软件UM,建立车辆-轨道耦合系统，分析直线线路上不同波长和波深的谐波激扰作用下轮轨滚动接触的动力响应、蠕滑率、蠕滑力等物理量的变化规律,以及波磨的发展特性,揭示谐波激扰引发的轮轨接触蠕滑特性。

2 谐波型波磨激扰模型的建立

严格地讲,轮轨间的激扰往往是随机的,如轨道几何状态不平顺[15,16]。但对于一些特定的轮轨激扰,研究者会采取简化的数学模型来模拟,如Steenbergen等[17]在分析焊缝凸头对轮轨动力响应影响时,将焊缝凸头用一个幅值为1 mm、波长为1 m的单波来模拟。韦红亮等[18]将高架支撑块轨道不平顺简化为波深和波长不同的一种单波激扰和两种连续的谐波激扰。蒋博等[19]将由轨下基础刚度不均等因素造成的轨道局部动态不平顺用指数衰减型函数来模拟。而铁路上普遍存在的周期特性显著的钢轨波磨,Grassie[20]曾根据成因不同将其分成六种类型,但不管属于哪种类型和成因,这些波磨都具有固定波长和位置的特征,可以将其简化为如图1(b)所示的多波连续谐波激扰，图1(a)为现场实测波磨照片,以更好的揭示轮轨接触蠕滑特性与初始谐波激扰的频率对应关系,即用余弦函数简单描述其轨面外形Z0(t)[21]，

(0≤t≤nλ/v)(1)

式中ω=2πv/λ。其中,a为不平顺波深,v为行车速度,t为行车时间,n为激扰波数,λ为不平顺波长。基于对上海某地铁线路钢轨波磨的实际测量,可得波磨波长范围为80 mm～300 mm,波深不超过1 mm,因此,本文建立的谐波激扰选取的波长分别为100 mm,200 mm和300 mm,波深分别为0.3 mm,0.6 mm和0.9 mm,列入表1。

3 车辆-轨道耦合模型的建立

3.1 车辆模型

以地铁A型车为研究对象,相关参数列入表2。

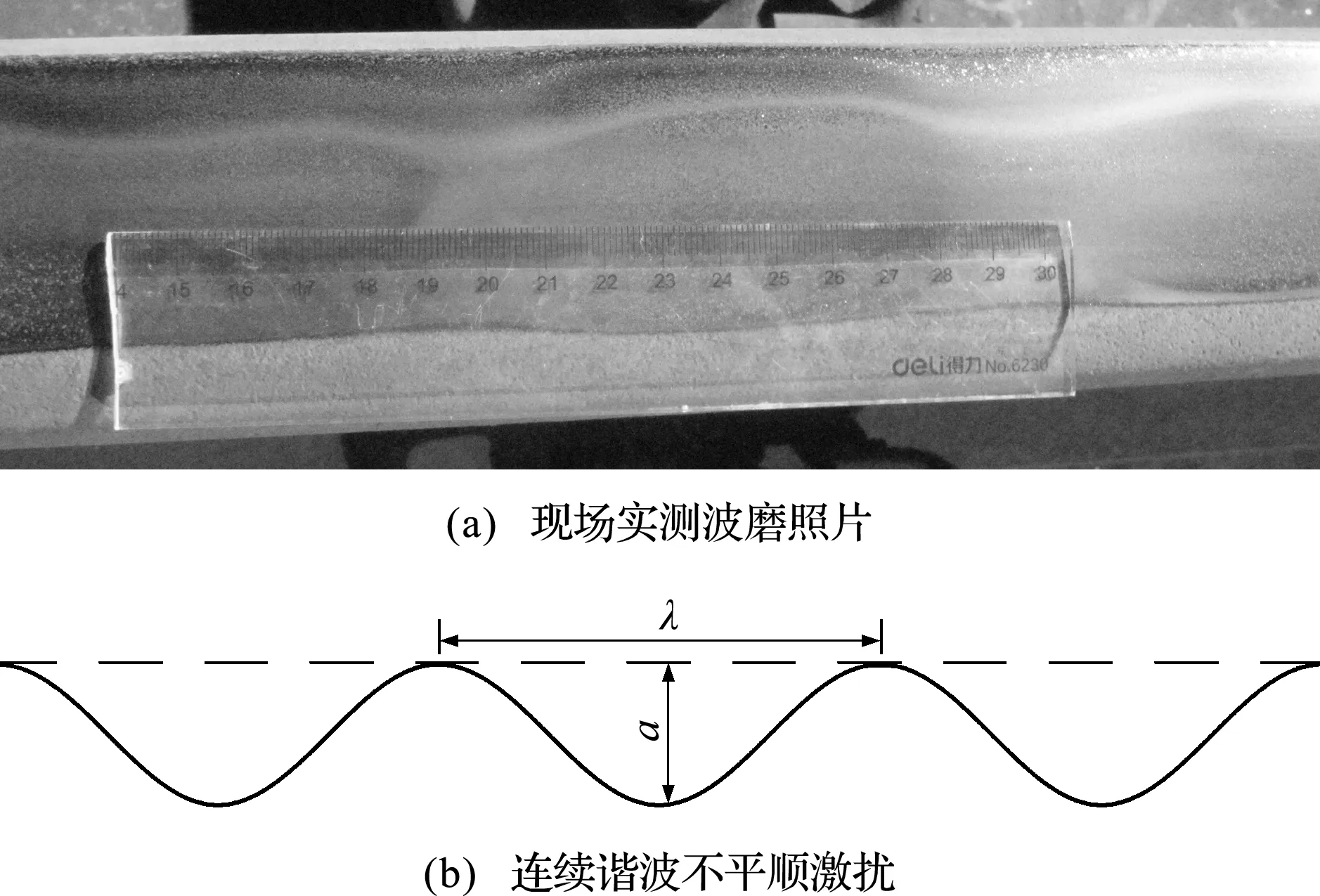
图1 波磨照片及其简化模型

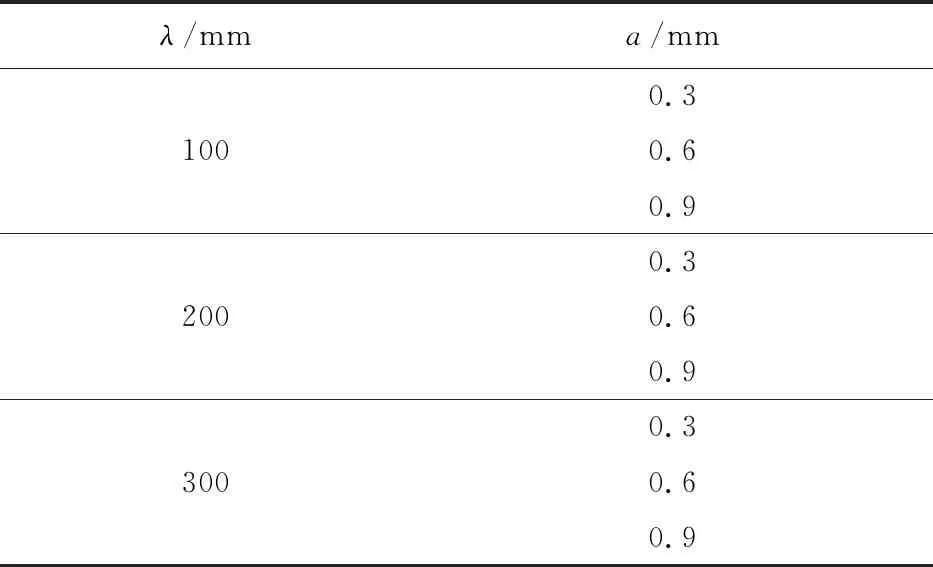
表1 λ和a的取值

运用多体动力学软件UM建立单节车辆模型,包含车体、构架和轮对3类质量体。车体与构架、构架与轮对之间通过弹簧阻尼单元连接,以模拟一系二系悬挂部件,具有三个方向上的刚度和阻尼。车辆模型如图2所示。

3.2 轨道模型

轨道模型采用柔性轨道模型。在柔性轨道模型中,钢轨模型采用能够考虑剪切变形的Timoshenko梁,其能较好地体现高频振动的影响。钢轨型号为60 kg/m,扣件间隔为625 mm。道床板采用有限元软件ABAQUS建模并作为子系统导入UM前处理中,该子系统通过力元与地基和钢轨进行连接,以模拟地基的支撑作用和扣件的连接作用,其中地基的支撑作用只保留垂向自由度,扣件部分保留垂向、横向和纵向三个方向上的自由度。道床板断面尺寸为2700 mm×300 mm,长度为 60 m。轮轨摩擦系数为0.35。轨道扣件类型采用科隆蛋扣件,垂向刚度为12.07 MN/m,横向刚度和纵向刚度为7.5 MN/m;垂向阻尼为1361.12 Ns/m,横向阻尼和纵向阻尼为974.67 Ns/m。轨道模型如图3所示。

表2 车辆参数

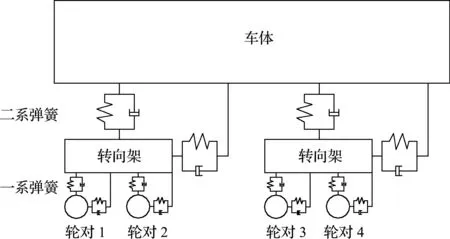
图2 车辆模型

3.3 轮轨接触模型

轮轨接触模型采用Kik-Piotrowski接触模型,该模型假设轮轨法向接触应力通过接触区域的几何点能够满足接触条件求得,切向接触问题通过改进的FASTSIM算法求解。该模型能够适应轮轨非赫兹接触的情况[22]。

基于上述车辆模型、轨道模型和轮轨接触模型,即可完成车辆-轨道耦合模型的构建,模型如 图4 所示。

3.4 模型验证

基于车辆-轨道耦合动力学模型,施加实测轨面不平顺作为钢轨表面初始不平顺,进而对某地地铁线路进行仿真计算。提取测点断面钢轨垂向振动加速度数据,并与实测数据进行对比,如图5所示,其中,实测数据来源于2018年10月对上海某地铁线路的试验结果。可以看出,仿真结果与测试结果吻合较好,验证了模型的有效性,满足本文计算精度要求。

将连续谐波激扰输入到车辆-轨道耦合动力学模型,然后运用动力学软件UM分别对3种波长(100 mm，200 mm和300 mm)和3种波深(0.3 mm，0.6 mm和0.9 mm)谐波激扰情形下的轮轨接触动力响应、轮轨蠕滑率和蠕滑力进行计算,分析轮轨接触蠕滑特性,并对波磨发展特性进行研究。仿真模型中的车速为60 km/h，因此三种波长对应的通过频率分别为167 Hz，83.3 Hz和55.6 Hz。

图3 轨道模型

图4 车辆-轨道耦合模型

4 轮轨接触蠕滑特性分析

4.1 轮轨接触动力响应特性

表1 的9种谐波激扰作用下的钢轨轮对垂向振动加速度最大值和平均值、轮轨垂向力最大值和平均值列入表3。由表3可知,在波长固定、波深增大时,钢轨轮对垂向振动加速度的平均值均增大(波长越短,增大幅度越大,即短波长类激扰对轮轨系统动力响应影响更大),轮轨垂向力的平均值变化不明显。在波深固定、波长增大时,钢轨轮对垂向振动加速度平均值均减小(波深越大,减小幅度越大,即大波深类激扰对轮轨系统动力响应影响更大),轮轨垂向力平均值变化不明显。当波长为100 mm,波深为0.9 mm时,钢轨轮对垂向振动加速度最大值和平均值、轮轨垂向力最大值均达到最大。其原因在于钢轨表面连续谐波激扰波长的减小会提高轮轨系统动力作用的频率,而连续谐波激扰波深的增大则会提高轮轨系统动力作用的强度。上述规律对于地铁线路养护维修具有一定的指导意义。

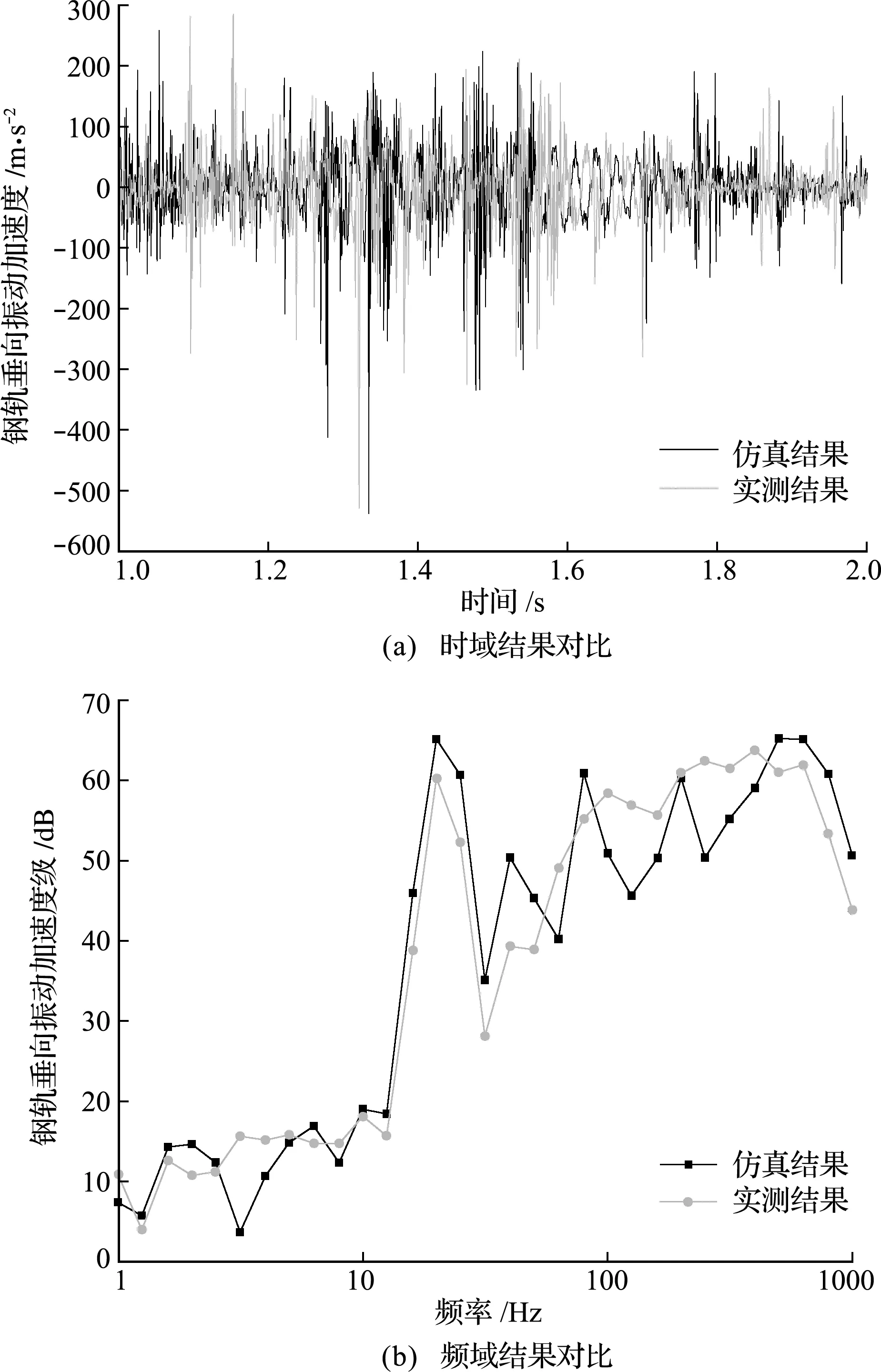
图5 仿真与实测结果对比

4.2 蠕滑率

通过计算可得9种工况下纵横向蠕滑率变化情况,分别提取其最大值和平均值列入表4。由 表4 可知,当波长固定,波深由0.3 mm增大至0.9 mm时,三种波长对应的纵向蠕滑率平均值分别增大139.3%，54.2%和8.3%,横向蠕滑率平均值分别减小83.2%，8.7%和8.5%;当波深固定,波长由100 mm增大至300 mm时,三种波深对应的纵向蠕滑率平均值分别减小71.4%，87.3%和87.1%,横向蠕滑率平均值分别增大26.3%，356.5%和589.3%。

为了反映蠕滑率变化情况,以波长100 mm的谐波激扰为例,截取计算区段中间部分进行频谱分析,如图6和图7所示。

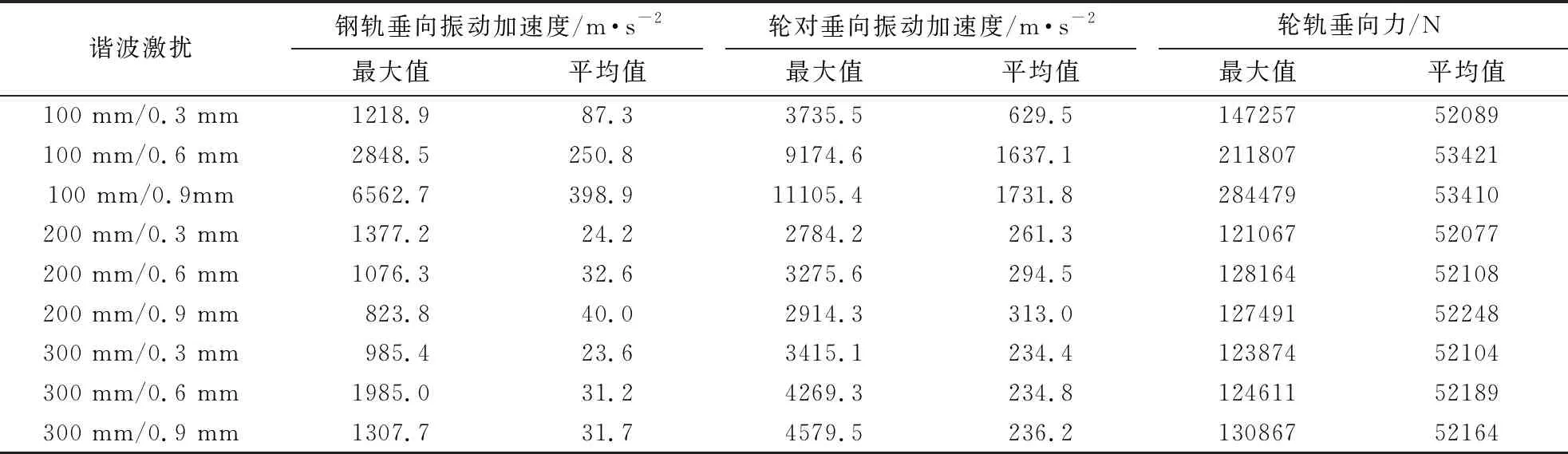
表3 不同谐波激扰波长和波深下的轮轨接触动力响应特性Tab.3 Dynamic response characteristics of wheel-rail contact under different harmonic excitation wavelengths and wave depths

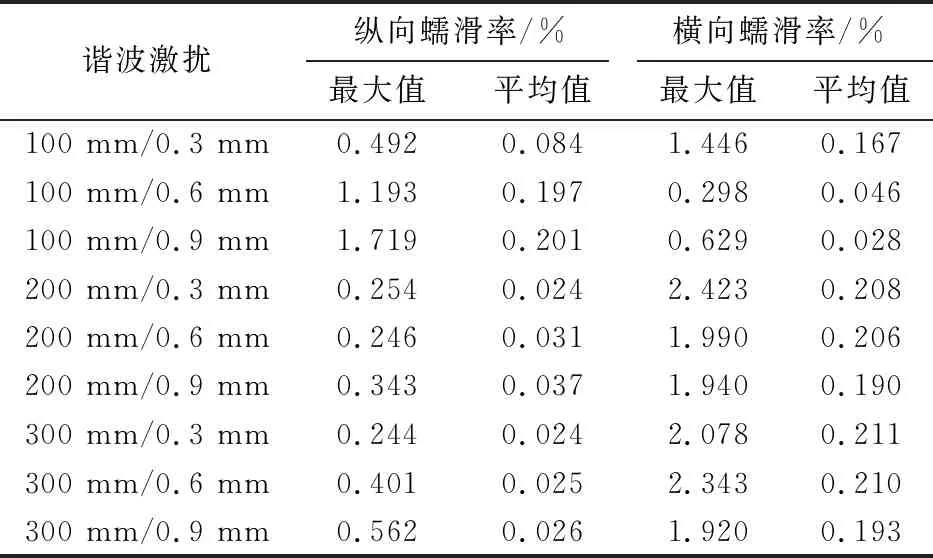
表4 不同谐波激扰波长和波深下的轮轨接触蠕滑率

可以看出，

(1) 纵向和横向蠕滑率均含有与初始不平顺频率值167 Hz相接近的频率成分。

(2) 纵向蠕滑率特征频率随着波深的增大趋向高频段发展,横向蠕滑率特征频率集中在低频段,且随着波深增大逐渐减小。

(3) 当波深为0.3 mm时,纵横向蠕滑率强度相当，二维特征明显，能量主要集中在低频,频率比较单一;当波深达到0.6 mm和0.9 mm时,蠕滑率以纵向蠕滑率为主,表现出多频率特征,说明此时波深的增大主要影响轮轨间的纵向相对速度,一维特征明显。

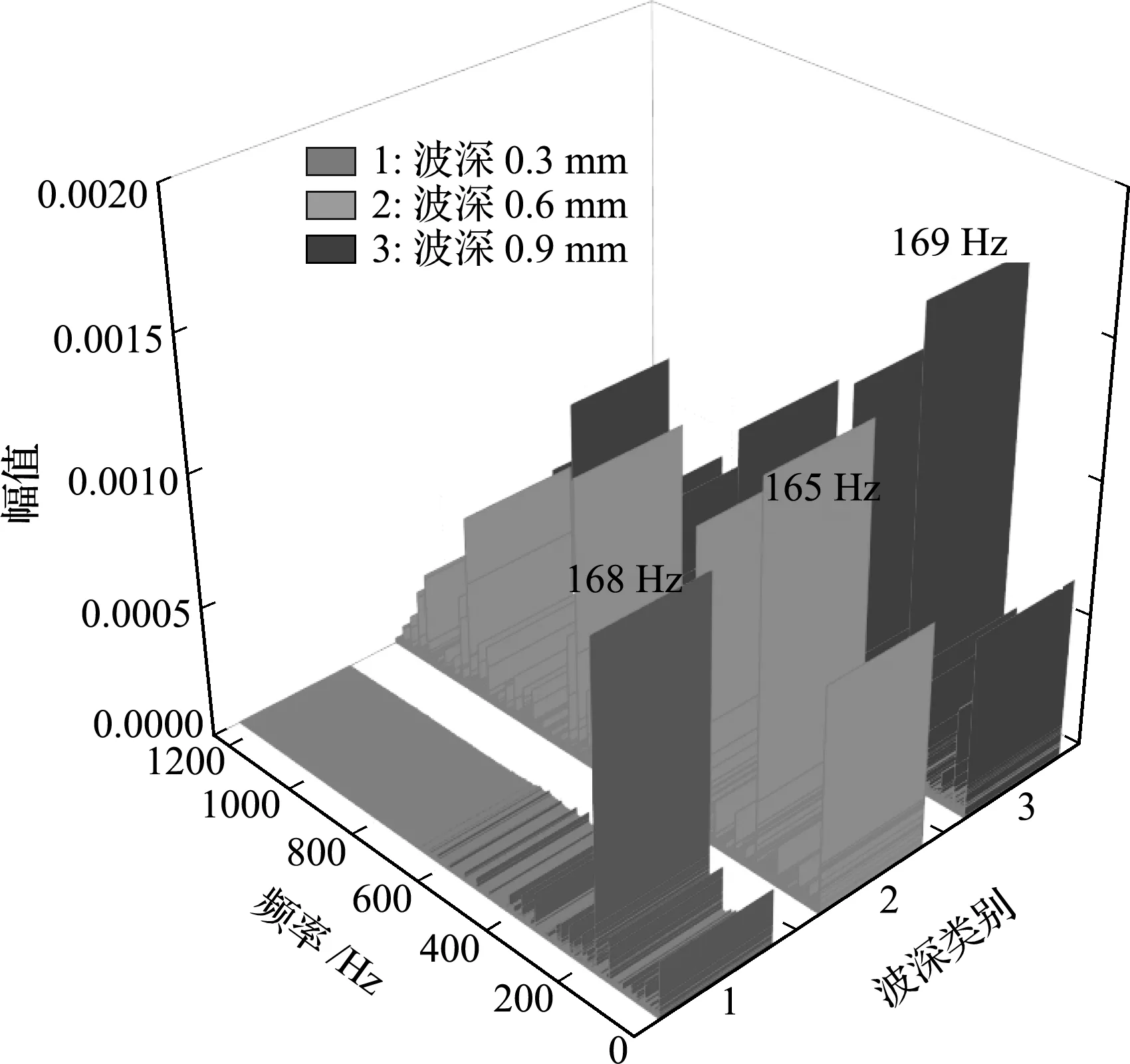
图6 纵向蠕滑率

图7 横向蠕滑率

4.3 蠕滑力

不同激扰波长和波深下的轮轨接触纵横向蠕滑力最大值和平均值列入表5。由表5可知,当波长固定,波深由0.3 mm增大至0.9 mm时,三种波长对应的纵向蠕滑力平均值分别增大117.9%，58.8%和22.7%,横向蠕滑力平均值随着波深的增大分别减小84.7%，18.4%和17.6%;当波深固定,波长由100 mm增大至300 mm时,三种波深对应的纵向蠕滑力平均值分别减小71.6%，83.8%和83.9%,横向蠕滑力则分别增大34.4%，525.7%和624.9%。

同样以波长为100 mm的谐波激扰为例,不同波深下的轮轨接触纵横向蠕滑力的频谱曲线如图8和图9所示。可以看出，

(1) 纵向和横向蠕滑力均含有与初始不平顺频率值167 Hz相接近的频率成分。

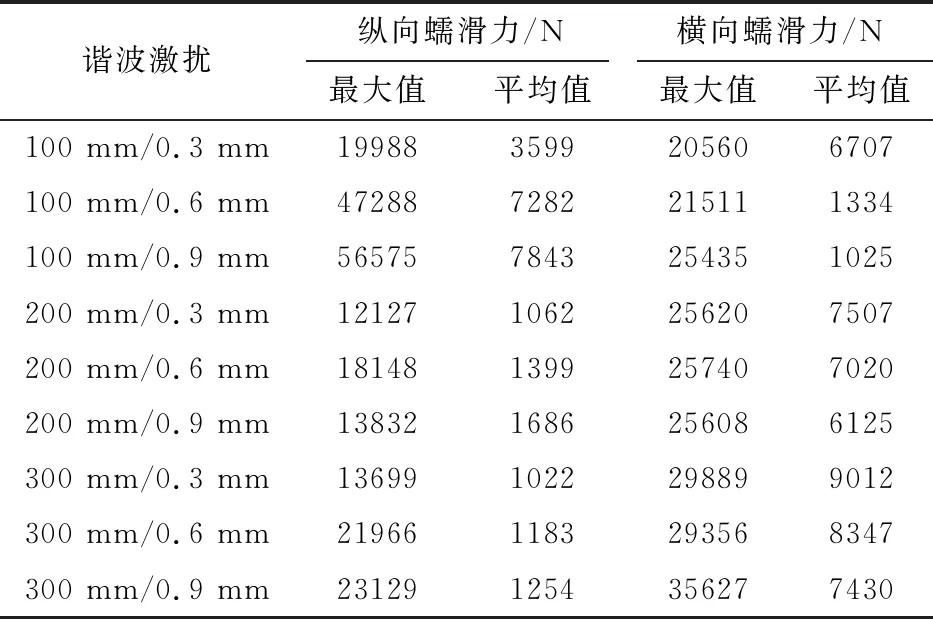
表5 不同谐波激扰波长和波深下的轮轨接触蠕滑力

(2) 纵向蠕滑力特征频率随着波深的增大趋向高频段发展,横向蠕滑力特征频率主要在低频段,且随着波深增大逐渐减小。

(3) 当波深为0.3 mm时,纵横向蠕滑力强度相当,二维特征明显,能量主要集中在低频,频率较为单一;当波深达到0.6 mm和0.9 mm时,蠕滑力以纵向蠕滑力为主,呈现多频率特征,一维特征明显。

5 谐波激扰下波磨发展特性研究

为了对连续谐波激扰下波磨的发展特性进行研究,以波深0.9 mm,波长分别为100 mm，200 mm和300 mm的三种谐波激扰为例,采用基于摩擦功理论的材料摩擦磨损计算模型对钢轨磨耗进行叠加计算[23]。取100000次运算为增量,在初始不平顺基础上输出5次(取其中3次)钢轨磨耗量曲线,然后对其进行频域变换,得到频谱如图10所示。同时对比频率160 Hz处不同波长的磨耗量,如图11所示。

(1) 如图10所示,随着运营时间的增加,三种波长对应的磨耗量在低频段增加较小,在中高频段增加较大。

(2) 如图11所示,随着运营时间的增加,波长为 100 m m 时，磨耗量从 1.28159 m m 增加到 5.40795 m m,增幅为4.12636 m m;波长为200 mm时，磨耗量从 0.28989 m m 增加到 1.24945 m m,增幅为 0.95956 m m;波长为 300 m m 时，磨耗量从0.24948 mm增加到 1.04739 m m,增幅为 0.79791 m m。说明在频率 160 H z 处，磨耗量幅值和磨耗发展速度都随着波长的增大而减小。

图8 纵向蠕滑力

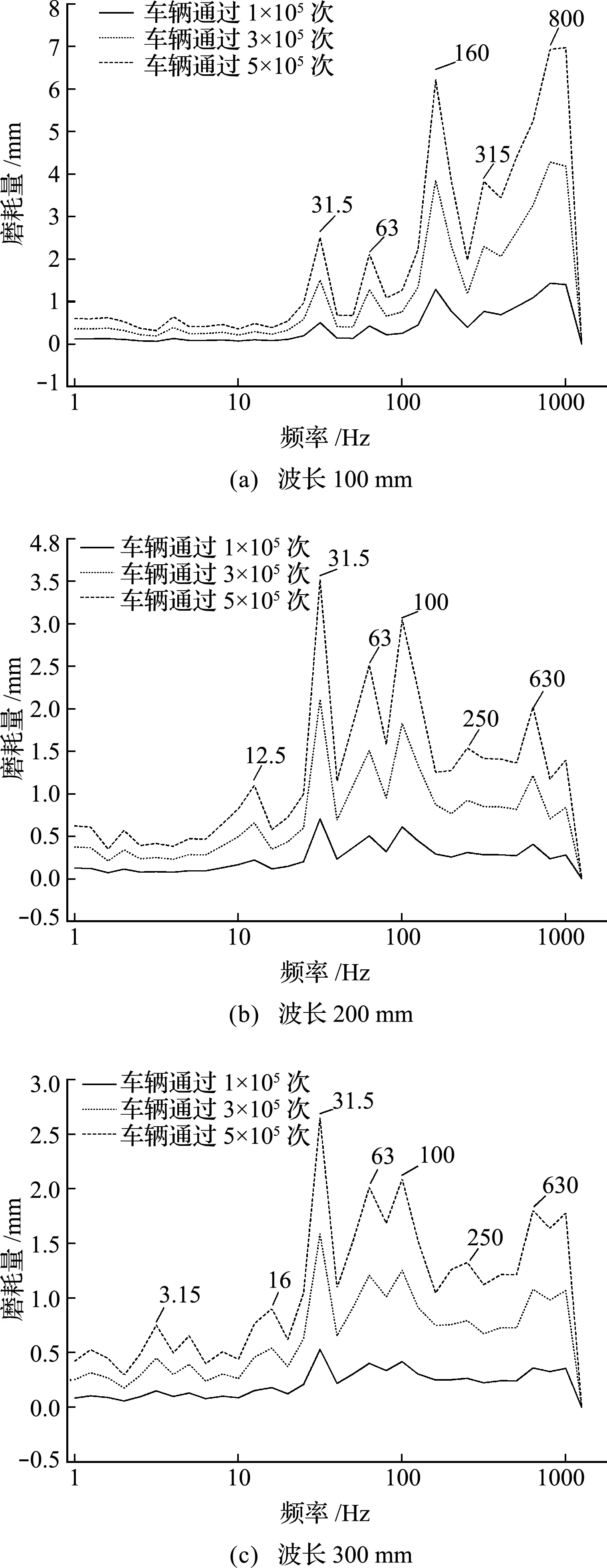
图10 磨耗量1/3倍频程

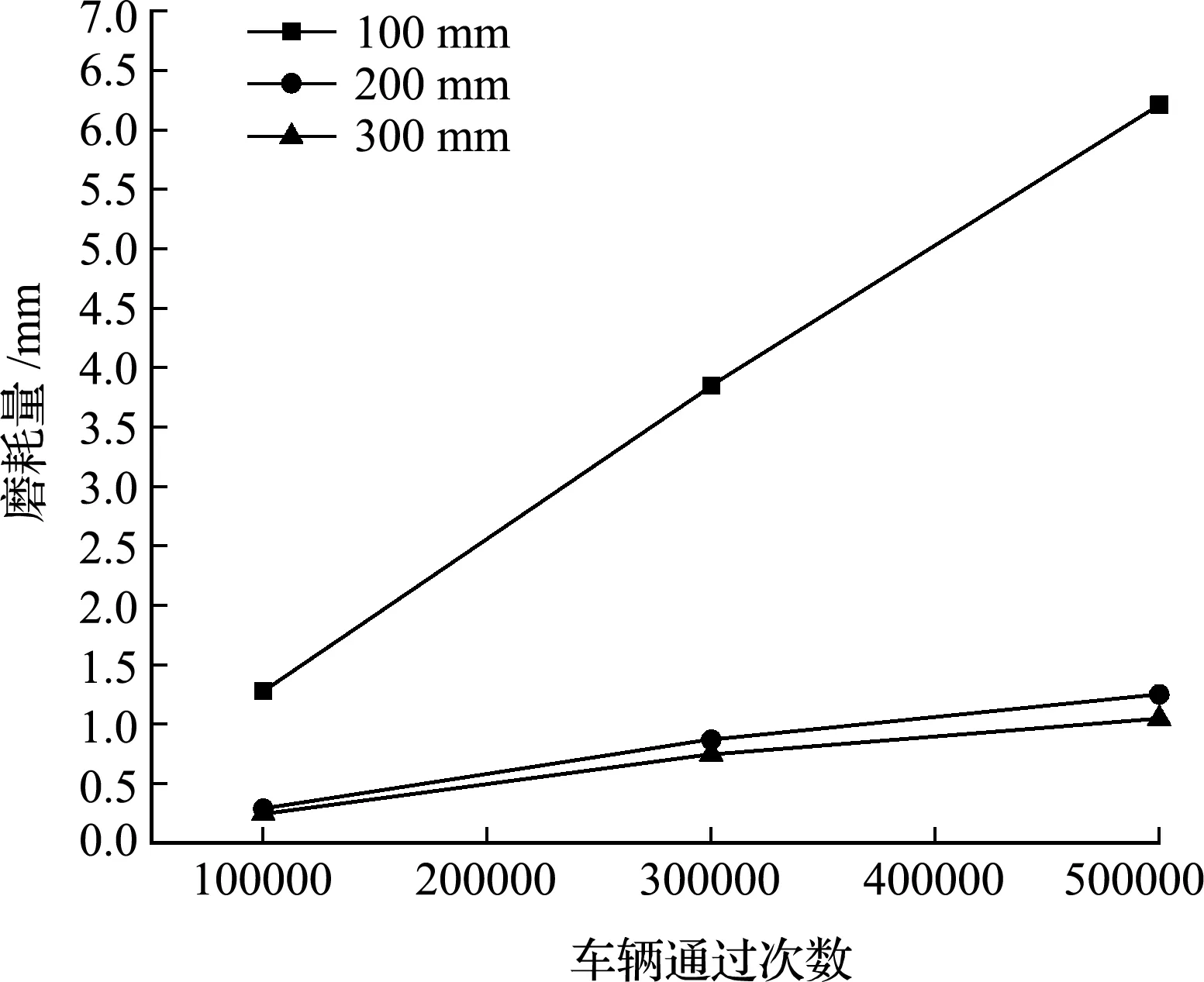
图11 不同波长下磨耗量对比

6 结 论

(1) 谐波激扰波长和波深对轮轨接触动力响应特性有着重要影响。在波长固定、波深增大时,钢轨轮对垂向振动加速度的平均值均增大,轮轨垂向力的平均值变化不明显。在波深固定、波长增大时,钢轨轮对垂向振动加速度平均值均减小,轮轨垂向力平均值变化不明显。且当波长为100 mm,波深为0.9 mm时,钢轨轮对垂向振动加速度最大值和平均值以及轮轨垂向力最大值均达到最大。

(2) 当波长固定,波深由0.3 mm增大至0.9 mm时,纵向蠕滑率/力平均值均增大,横向蠕滑率/力均减小;当波深固定,波长由100 mm增大至300 mm时,横向蠕滑率/力平均值均增大,纵向蠕滑率/力均减小。

(3) 对于波长100 mm的谐波激扰,纵横向蠕滑率/力均含有与初始不平顺频率值167 Hz相接近的特征频率成分。纵向蠕滑率/力特征频率随着波深的增大趋向高频段发展,横向蠕滑率/力特征频率集中在低频段,且随着波深增大逐渐减小。当波深为0.3 mm时,纵横向蠕滑率/力强度相当,能量主要集中在低频,频率比较单一;当波深达到0.6 mm和0.9 mm时,蠕滑率/力以纵向蠕滑率/力为主,表现出多频率特征。

(4) 在波长相同的条件下,随着运营时间的增加,磨耗量在低频段增加较小,在中高频段增加较大。