地下水流并行有限层方法及同伦反演研究
王少伟, 徐 进, 杨伟涛
(烟台大学 土木工程学院,烟台 264005)
1 引 言
地下水是宝贵的自然资源,也是地质环境的基本要素[1]。过量开采地下水会造成区域性降落漏斗,导致地面沉降和海水入侵等环境地质问题。实现地下水流问题的高效求解对上述问题的预测和防治具有重要意义。
地下水流问题的常用求解方法包括解析法和数值法等。解析法[2,3]是利用积分变换等分析手段直接求解地下水流控制方程,得到问题的精确显式解。Craig[4]提出了二维非均质稳定流问题的一般解,解的形式包括拉普拉斯方程的复多项式以及由多项式系数确定的附加非全纯项,可以通过选择多项式系数满足不同边界的流动条件。Zha等[5]定义了无限边界、等效均质含水层中抽水引起的二维和三维水流的近似稳态解及稳态条件,讨论了非均质含水层的稳态解条件。然而,对于考虑复杂非均质性和各向异性情形的三维地下水流问题,目前解析法仍难以应用。
数值方法(有限差分法和有限单元法等)是目前求解地下水流模型的主流方法,可以反映复杂水文地质条件下的水流形态,得到广泛研究和应用。潘树来等[6]提出了一种无需对自由面作近似处理的精确算法,为实现有自由面非稳定渗流问题的精细分析提供技术保证。Xie等[7]提出了一种新的有限体积多尺度有限元模型,该方法可以简化仿真过程,有效模拟多孔介质中的地下水流动。但是,在对区域性地下水流三维非稳定流的精细化分析时,目前的数值方法仍然存在计算工作量大和计算时间长等问题[8,9]。除了传统解析法和数值法,有限层方法[10]是一种混合算法,将解析手段和数值方法相结合,使得三维问题简化为一维问题,可以实现地下水流模型的高效求解[11-14]。
值得注意的是,随着地下水流模型的不断完善,理论计算与数值模拟中涉及到的参数需要事先确定。如何通过实验或现场资料有效获取各类水文地质参数非常重要[15-19]。然而,反演分析中需要多次调用正演程序,这加剧了数值方法本身存在的计算困难。另外,反演计算本身存在初值选择问题,如果初值选取不合适,太过偏离真值,往往会出现收敛速度慢、局部收敛甚至发散等问题。本文主要结合同伦算法对参数反演方法进行改进,Keller等[20]首次将同伦法用于反演方法中,使得同伦算法的研究得到了迅速发展。文献[21,22]利用同伦方法对不同模型参数进行反演计算,结果表明,同伦参数反演方法具有良好的稳定性、收敛性和较快的计算速度。
本文针对地下水流有限层求解格式的解耦性,实现并行化,进一步提高其处理地下水三维流问题的计算效率。同时,结合大范围收敛的非线性同伦方法[23,24]进行反演计算,避免初值选取问题。在此基础上,利用MATLAB编制并行化计算程序和同伦反演程序,并通过算例对比验证方法和程序的有效性和高效性。
2 地下水数学模型
根据质量守恒定律和达西定律,在直角坐标系下,地下水三维、非稳定流的数学模型用降深可表示为
(1)
式中S(x,y,z,t)为降深(L),Kx,Ky和Kz分别为x,y和z方向的渗透系数(LT-1),q(x,y,z,t)为汇源项(T-1),Ss为贮水率(L-1)。Sy为给水度(无量纲),反映了潜水面单位降深重力排水的补给强度,当考虑承压水流时,可以令Sy=0。
式(1)是地下水三维流的正演数学模型。对于参数反演问题,主要依据实测水位或者降深结果来反求含水层的未知水文地质参数,使得
S(xi,yi,zi,tj)=Sc(xi,yi,zi,tj)
(2)
式中S(xi,yi,zi,tj)为计算降深值,Sc(xi,yi,zi,tj) 为i位置在j时刻的实测降深值。在求解地下水流正演数学模型(1)的基础上,结合一定的优化算法可以实现对反问题(2)的分析。
3 有限层求解格式及其并行特点
根据含水层系统的层状非均质特点,将含水层系统沿z方向离散成L个不同厚度的层元,每一层可以具有不同的水文地质参数以考虑这种层状非均质。
3.1 有限层求解格式
降深在平面x和y方向分别选用M和N项正交完备的解析函数系表示,z方向则采用常规有限元线性形函数来离散,最终得到解析数值混合形式的降深试探函数[12]。
将降深试探函数代入正演数学模型(1),基于伽辽金原理或者泛函极值原理,可以得到正演数学模型的求解格式,用矩阵形式表示为[12]
(3)
式中[G]和[B]分别为整体渗透矩阵以及整体贮水矩阵,{Q}为水量向量,{Φ}为总待求系数向量。
3.2 求解格式的特点
(1) 求解格式(3)的[G]和[B]等整体系数矩阵和向量具有显式的解析表达式,无需数值积分。与传统的数值方法相比,极大减轻了计算工作量,节省了运算时间。矩阵元素具体解析式详见文献[12]。
(2) 利用所引入解析函数的正交性,可以实现求解格式(3)的整体解耦,将其拆分为M×N个独立的L+1阶子线性系统,拆分后的系数矩阵[G]和[B]如图1所示。
(3) 整体矩阵拆解后的子矩阵互不耦合,相互独立,可以分别求解,具有天然的并行性。利用这一特点进行并行计算时,各进程之间无需数据交换,不同进程单独处理,节省运算时间。
4 求解格式并行化方法
结合地下水流有限层求解格式的上述特点,利用MATLAB并行计算库,对求解格式(3)进行并行化处理。
针对求解格式关于级数项M和N的解耦性,采用SPMD(single program multiple data)的方式进行并行化处理[25]。通过SPMD和End命令定义一个SPMD并行结构代码段,各进程使用相同主程序,具有不同数据。程序中使用parpool(K)或parpool指令打开MATLAB并行池,打开K个线程(worker)或默认线程。根据worker的数目,利用labindex命令将级数项M和N分成M1,M2,…,Mi和N1,N2,…,Nj组数据,分别计算降深值(i和j通过worker数目决定)。
根据求解格式特点,各进程单独计算,无需通讯环节,待各进程计算结束,将结果返还给直接累加,可以得到最终降深值,程序流程如图2所示。
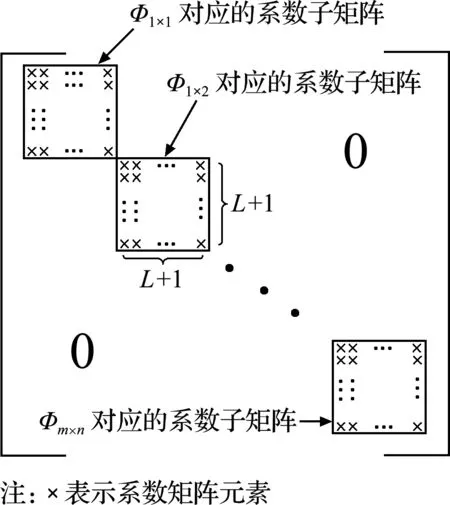
图1 整体系数矩阵的解耦性
5 地下水流降深反演计算
在并行正演方法的基础上,使用同伦方法进行反演计算。同伦方法是一种非线性优化算法,主要采用逐步逼近的计算方式对初值逐次优化,具有大范围收敛的特点。
同伦方法的基本思想是将一个简单问题与所要求的复杂问题放到一个一般问题中,首先求出简单问题的解,然后逐次连续过渡到复杂目标问题的解[23,24]。
(4)
根据同伦方法的思想,构造如下同伦函数
(5)

(6)
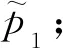
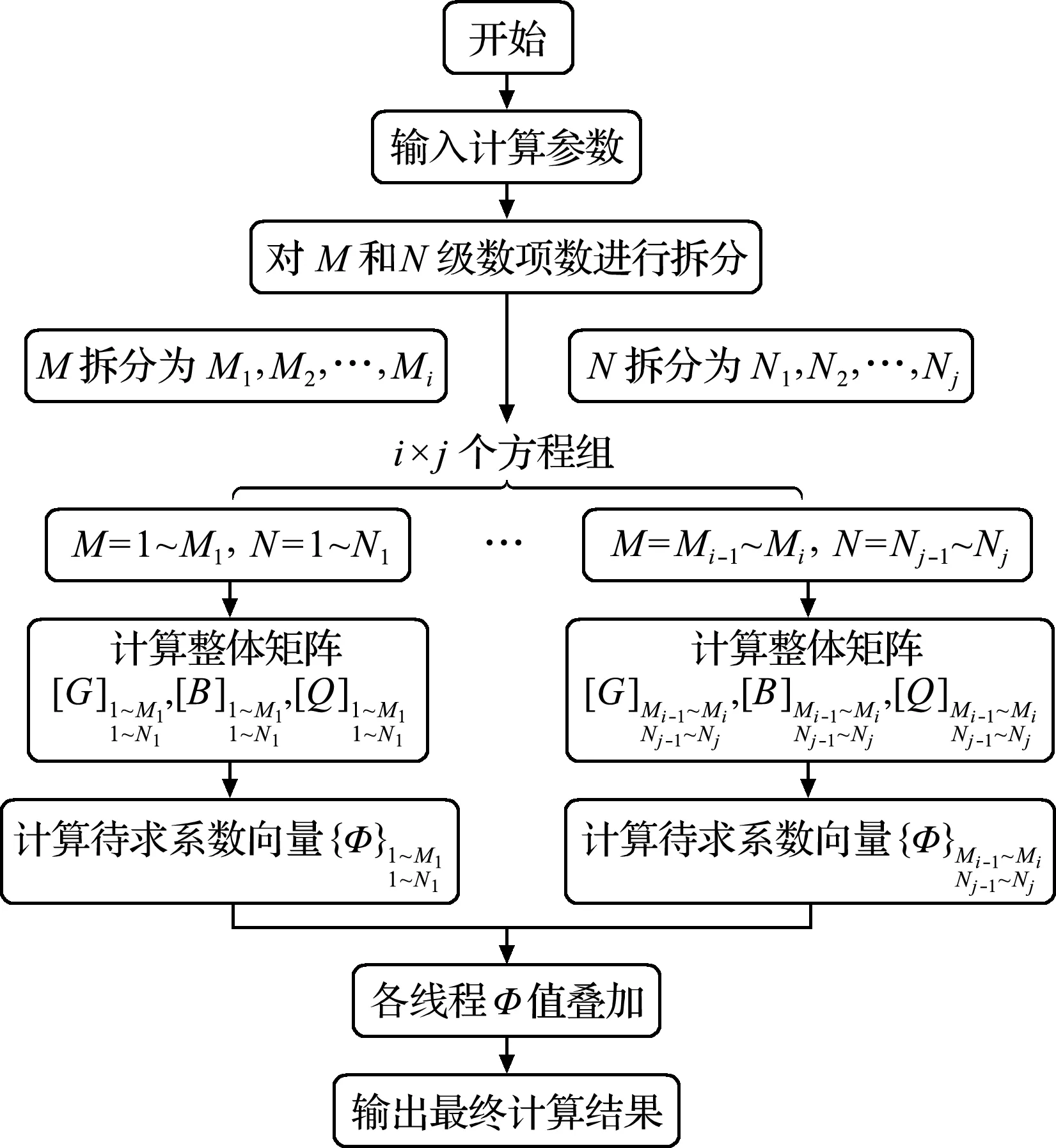
图2 降深正演并行计算程序流程
6 数值算例及验证
根据上述并行策略和反演算法,分别编写MATLAB计算程序以实现地下水流正反演问题的分析。为了验证本文方法和计算程序的正确性,选取了承压水完整井、多层结构含水层系统非稳定流问题进行了分析,并与已有解答进行对比。最后,通过数值算例探讨并行程序的计算效率和反演程序的收敛性。
6.1 单层承压含水层的地下水流分析
利用本文计算程序对经典的单层承压含水层完整井引起的地下水非稳定流问题进行计算。在算例中,含水层厚度c=100 m,贮水率Ss=2×10-5/m,渗透系数Kx=Ky=Kz=5 m/d,抽水量Q=2000 m3/d。利用计算结果,图4给出了距离井中心x=y=10 m处不同时刻的完整井抽水降深曲线,可以看出本文解与文献[26]的解析解曲线非常吻合,证明了并行化正演程序的正确性和计算精度。
6.2 多层含水层系统的地下水三维流分析
为了验证并行正演程序处理复杂地下水流问题的能力,选取三层结构含水层系统三维流问题进行了分析,如图5所示,整个含水层由厚为20 m的第一承压含水层、中间厚为10 m的弱透水层和厚为30 m的第二承压含水层组成,各层的水文地质参数见文献[12]。
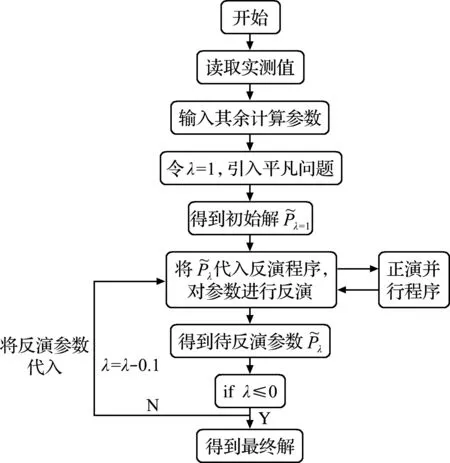
图3 降深反演计算并行程序流程
利用本文计算结果,图5分别给出了第一承压含水层和开采含水层顶板处的降深随距离的分布曲线。由于问题的复杂性,不存在方便对比的解析解,本文采用有限差分计算结果进行了对比。可以看出,本文并行解答与有限差分结果有较好的拟合度,计算结果很好地反映了多层结构含水层的地下水三维越流特征。
6.3 单层含水层地下水流模型参数反演分析
为了验证本文地下水流同伦反演程序的正确性,设置一单层承压含水层抽水降深算例,利用Theis解,代入算例6.1计算参数生成水位降深时间序列,记录时间段为t=0 d~2 d,时间间隔为Δt= 0.1 d,测点坐标为x=y=10 m。将该降深时间序列作为反演计算中的实测值,假定K为未知参数进行反演。
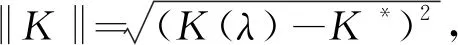
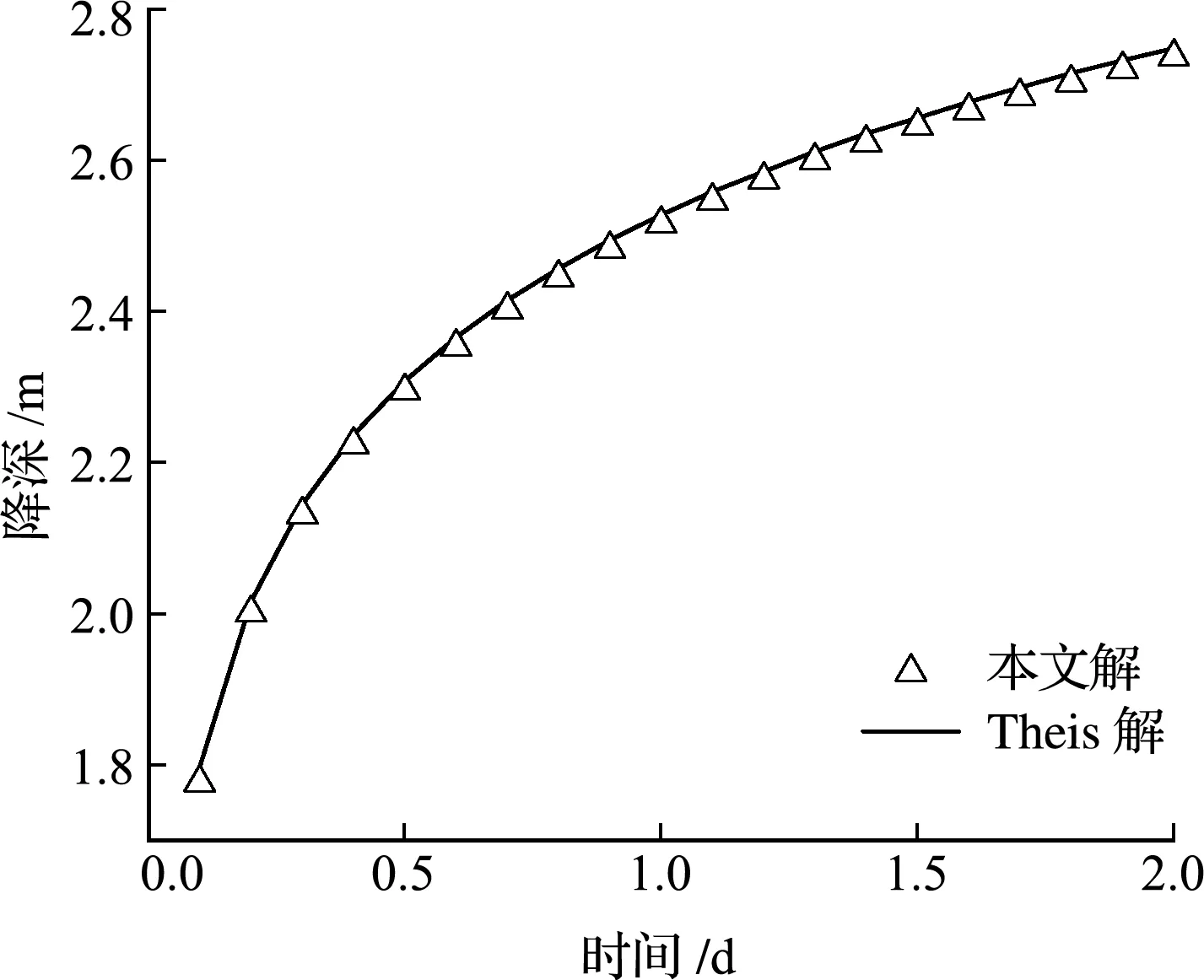
图4 承压含水层完整井引起的水位降深曲线

图5 三层结构承压含水层水位降深
6.4 多层结构含水层地下水流模型参数反演分析
利用算例6.2的计算参数,记第一和第二两含水层的渗透系数分别为K1和K2,通过正演程序计算生成含水层顶和底板距井点10 m处的降深时间序列 (记录时间段为t=0 d~2 d,时间间隔为 Δt=0.1 d),以此作为资料代入同伦程序来反演渗透系数K1和K2。
将初始值选为K0=(10,10) m/d,同伦曲线如图7所示,其中
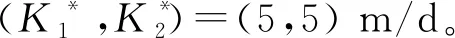
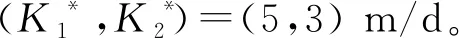
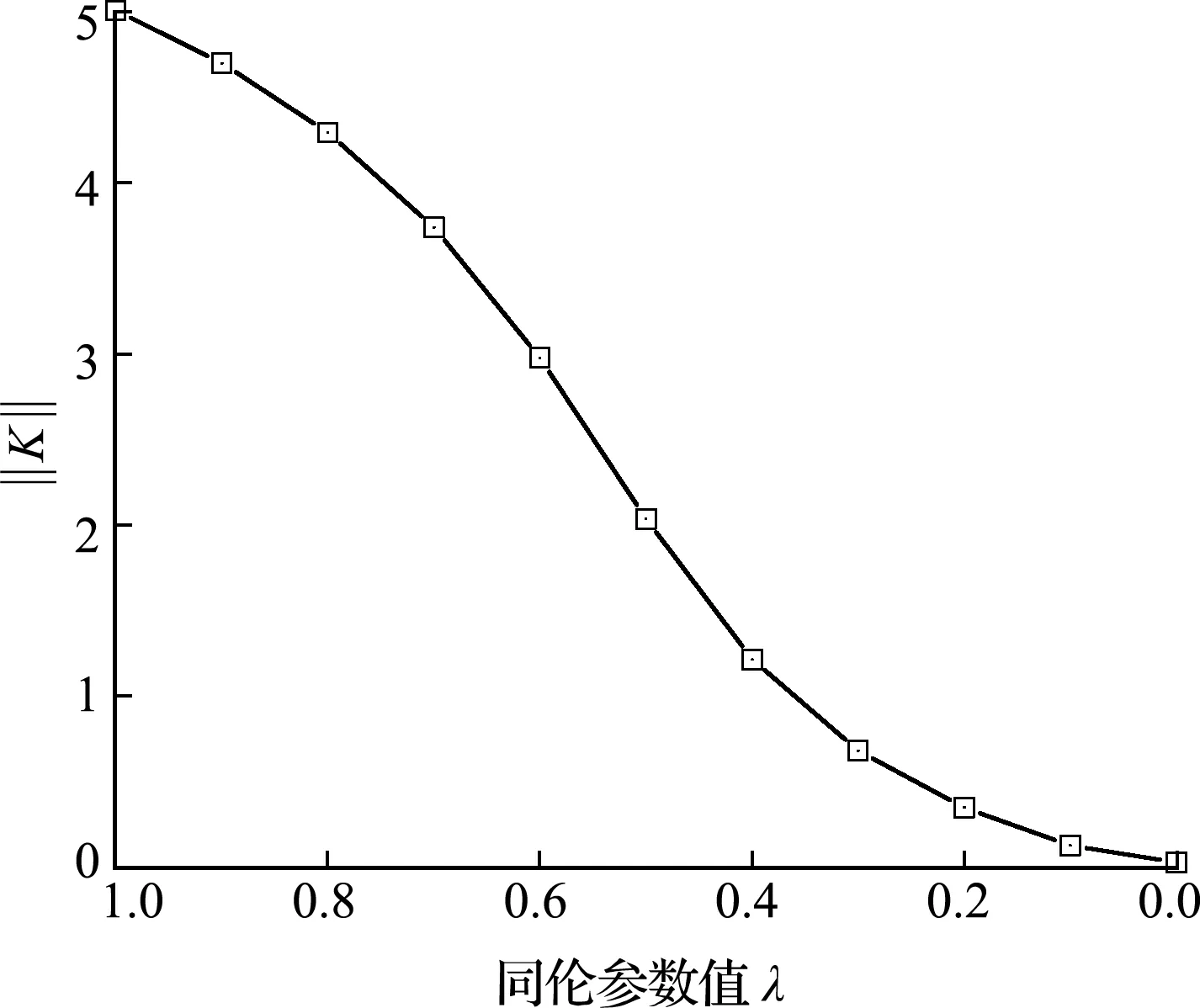
图6 参数反演同伦曲线
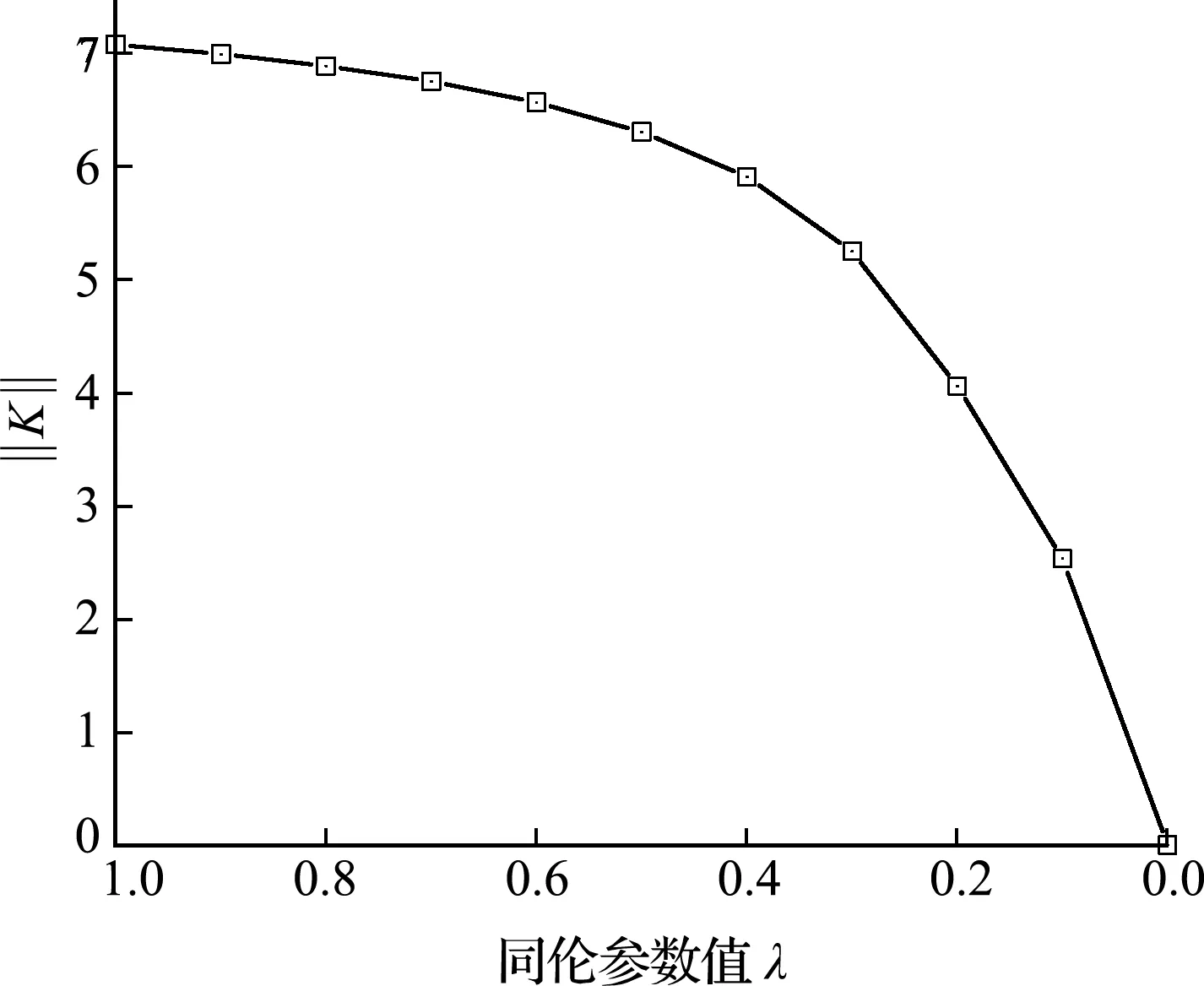
图7 参数反演同伦曲线
6.5 并行计算效率分析
利用有限层求解格式存在的解耦性进行并行化处理,从而达到提高计算效率的目的。区别于有限元等纯数值方法,所采用的解析函数项M和N对有限层方法计算结果的精度有重要影响。为了说明并行求解效率,针对不同解析级数项数,对比反演计算中不同线程的运算时间,计算机硬件配置列入表2。
计算中将计算时间固定,生成一组距井点不同位置的降深值作为反演实测值。反演计算中采用四线程并行程序,观察在不同级数项数下的串行和并行运算时间。图8将计算时间固定为1 d,由曲线可以看出,当级数项数较小时,并行运算时间要高于串行计算;计算循环量大于60时,并行优化的高效性开始体现;在100项处,计算效率提升了近 1倍。这是由于并行反演计算程序较为复杂,程序间存在数据传输问题,占用一定运行时间。
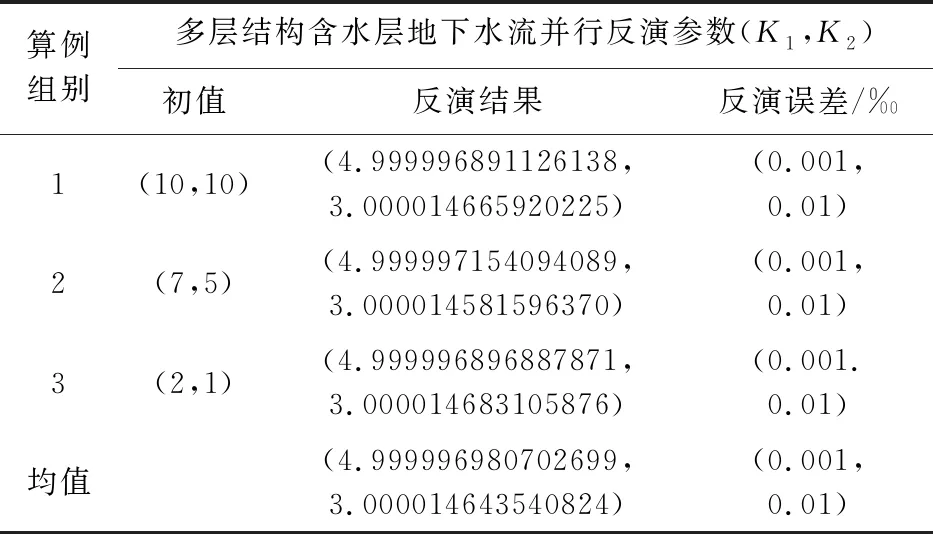
表1 选取不同初值情况下的反演计算结果

表2 计算机配置
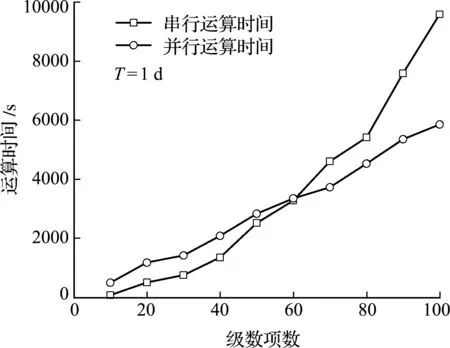
图8 不同函数级数项下的并行计算效率对比
7 结 论
(1) 基于地下水流三维有限层求解格式,建立了该方法的并行化算法,通过MATLAB编制相应程序实现了地下水流有限层方法的并行化,利用解析解以及有限差分解验证了并行方法与计算程序的正确性。
(2) 利用上述并行算法作为正演程序,基于非线性同伦原理,进一步开发了地下水参数反演程序,利用数值算例验证了程序的正确性;同时,研究表明同伦反演算法不依赖于参数的初值选取,具有大范围收敛的特点,适用于地下水流反演计算问题的数值求解。
(3) 通过数值算例说明了并行化程序的计算效率。利用本文并行算法的解耦性,在并行计算中可以节省计算成本,便于编程实现。

