基于有限元的绞缆机卷筒结构优化及稳定性分析

董有凡，胡 义，耿国祥，王 帆

(武汉理工大学 船海与能源动力工程学院，湖北 武汉 430063)

随着航运业的不断发展，船舶的吨位变得越来越大，载重量也随之上升，船舶大型化是未来发展的一个趋势。绞缆机是船舶主要设备之一，卷筒作为绞缆机重要的承载部件，其结构设计的可靠性对于保障绞缆机安全运行而言极为关键。由于对绞缆机卷筒缺乏精确计算，使得绞缆机卷筒的理论承载能力远大于实际所受的负载，造成卷筒自身重量过大，使得在生产过程中存在材料的浪费，增加了生产成本，造成了一定的经济损失。目前，对于卷筒的研究大多数通过有限元计算分析来校核，如胡甫才对卷筒进行有限元计算分析，然后通过试验验证了有限元模型的正确性[1]。翟庆光利用微积分学原理对钢缆在卷筒上张力进行分析，并通过实例进行验证[2]。本文对卷筒理论载荷进行分析，用SolidWorks建立绞缆机卷筒三维实体模型，导入Ansys Workbench中对卷筒进行有限元仿真分析，结果表明在支持负载下卷筒最大应力远小于许用应力值。在此基础上对卷筒筒壳进行结构优化设计和强度校核，在满足卷筒强度和刚度要求的情况下得到卷筒优化模型，经优化设计后的卷筒减重12.8%。总结3种不同的稳定性计算方法，对美国船级社(ABS)规范法、文献法和有限元法进行讨论分析。对优化设计后卷筒进行屈曲分析，结果表明优化后卷筒稳定性满足要求。对卷筒的优化设计实现了轻量化的目的，也为绞缆机卷筒的设计提供了理论依据。

1 卷筒理论载荷分析

为了计算出卷筒所受载荷大小，取缆绳作为研究对象，对其进行受力分析，缆绳受力示意图如图1所示。图1中F1为入绳端缆绳拉力；F2为出绳端缆绳拉力；d为卷筒直径；P1为缆绳与卷筒之间的径向压力；β为缆绳缠绕在卷筒上形成的夹角。缆绳缠绕在卷筒的拉力符合欧拉递减规律，即F1=F0e-fθ，其中，f为缆绳与筒体间摩擦因数，F0为入绳端缆绳张力，θ为两侧包角的平均值。

图1 缆绳受力示意图

根据力在径向平衡可得：

(1)

卷筒表面所受径向压力P2：

(2)

式中，θ1、θ2分别为两侧包角，由于所取缆绳极小，所以θ1≈θ2，取其平均值θ；D为缆绳的直径。整理式(2)可得：

P2=(2F0/dD)e-fθ。

(3)

令P2=P0e-fθ,可得：

(4)

式中，P0为缆绳刚接触卷筒时，缆绳对卷筒的径向压力。

2 卷筒有限元分析

2.1 有限元模型建立

绞缆机卷筒参数如下：卷筒长度790 mm，卷筒半径355 mm，缆绳直径50 mm，筒壳厚度35 mm。绞缆机工况为：支持负载下缆绳拉力为450 kN。绞缆机卷筒筒体材料定义为DH36，侧板材料定义为 Q235B，轮毂材料定义为35#钢，绞缆机卷筒材料参数如表1所示。

表1 绞缆机卷筒材料参数

网格划分对绞缆机卷筒模型有限元分析的过程起着决定性作用，网格划分需要考虑到很多因素，是一个繁琐的过程，一般来说，计算结果精度的提升是随着网格数量增加的，但是相对应的计算量也将增大许多。对卷筒有限元模型进行网格划分，单元数为71 534，节点数为220 311。

2.2 有限元仿真结果分析

缆绳作用下，卷筒筒体为主要承载部位，由于缆绳与卷筒筒体间存在摩擦力，所以随着缆绳在卷筒筒体上面缠绕，原先缆绳作用于筒体的径向压力减小。根据研究表明，这种径向压力的减小符合欧拉递减规律。同时由简支梁的模型可知，卷筒中间出绳时，卷筒所受应力最大。

支持负载是绞缆机带式制动器在单层缆绳作用下所保持的最大拉力，所以卷筒在支持负载下仅考虑单层缆绳作用。经有限元分析，卷筒所受最大位移为0.31 mm，最大应力为125.43 MPa。取卷筒安全系数为2[3]，则卷筒许用应力值为177.5 MPa，支持负载作用下绞缆机卷筒最大应力值远小于许用应力值，存在优化空间。支持负载下卷筒应力和变形云图如图2、图3所示。

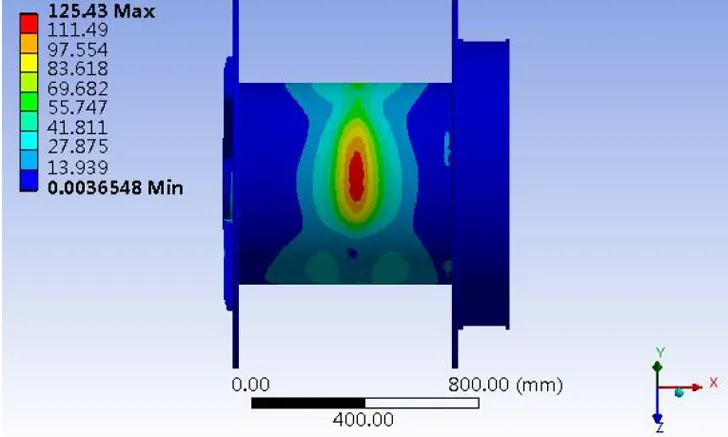
图2 支持负载下卷筒应力云图

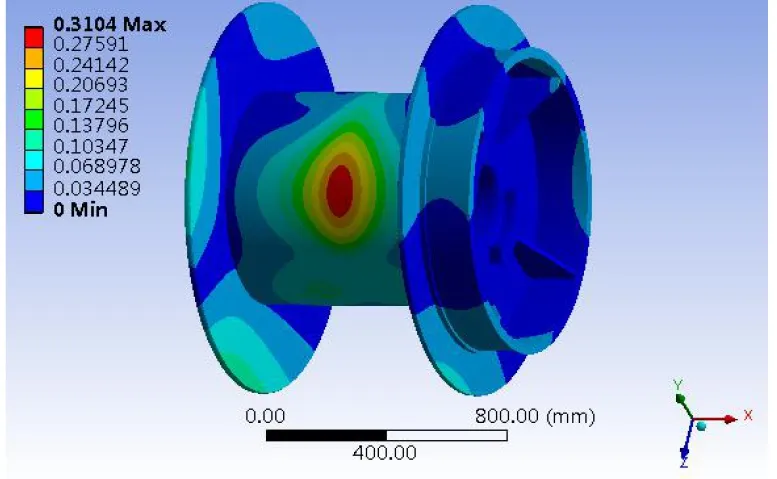
图3 支持负载下卷筒变形云图

3 卷筒筒壳优化设计

由以上分析可知，传统设计方法过于保守，绞缆机卷筒自身重量过大，因此考虑在满足卷筒强度和刚度要求的情况下减轻结构重量。通过减小筒壳厚度然后在结构内部加筋的方法，对卷筒结构进行优化设计。卷简优化后结构如图4所示。

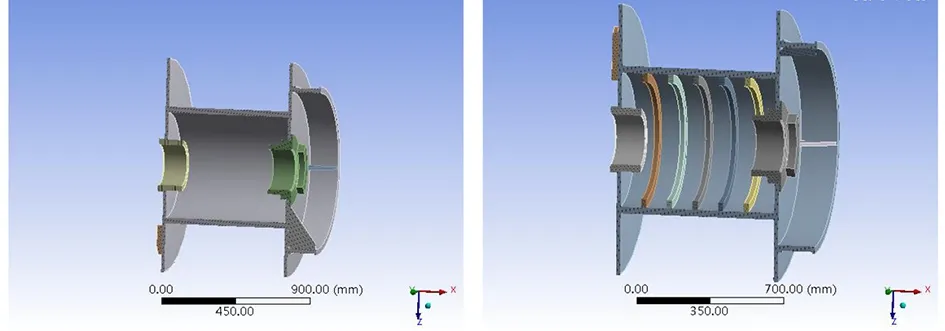
(a)优化前 (b)优化后图4 卷筒优化后结构

3.1 优化后仿真分析

为了确定结构优化后卷筒筒壳厚度，采用每次减少3 mm筒壳厚度的逼近处理方法，分别取筒壳厚度为32 mm、29 mm、26 mm、23 mm、20 mm，对其进行有限元分析，得到不同筒壳厚度下卷筒有限元计算结果，如表2所示。

表2 不同筒壳厚度下卷筒有限元计算结果

通过表2可知，当筒壳厚度降为20 mm时，卷筒最大应力超过许用应力值，卷筒失效，所以取筒壳厚度23 mm为最终优化结果。筒壳厚度为23 mm时卷筒应力和变形云图如图5、图6所示。

图5 筒壳厚度为23 mm时卷筒应力云图

图6 筒壳厚度为23 mm时卷筒变形云图

3.2 优化后结果分析

优化后卷筒最大应力为172.02 MPa，小于卷筒许用应力值177.5 MPa。卷筒最大变形为0.41 mm，均满足卷筒强度和刚度要求。优化前卷筒质量为1 060.13 kg,优化后卷筒质量为924.29 kg，减重12.8%，轻量化效果明显。

4 屈曲分析

由于绞缆机卷筒属于弹性薄壳结构，在缆绳作用下不仅要考虑卷筒强度，还要考虑屈曲的稳定性，由于大型外压容器很难通过对其进行外压试验来校核稳定性，所以大型外压容器通常采用理论计算和有限元计算方法[4]。

4.1 卷筒稳定性计算方法

1)ABS规范法。ABS采用铁摩辛柯基于圆环屈曲理论提出的无端板长圆管承受外压时的稳定理论[5]。临界公式为：

(5)

式中，Pcr1为ABS规范计算的卷筒临界应力；E为材料的弹性模量；μ为泊松比；h为圆管壁厚；R为圆管半径。代入数据，通过计算可得Pcr1=55.29 MPa。

2)文献法。传统的卷筒稳定性计算方法过于保守，因此许多学者对卷筒稳定性计算方法进行了深入研究，文献[6]通过李兹法得出了卷筒在径向压力作用下稳定性计算方法，卷筒所受临界应力Pcr2为：

(6)

式中，L为卷筒长度；L0为卷筒载荷作用长度；α=π/L；n为卷筒失稳时沿壳的圆周方向形成的半波数，具体计算方法为：

(7)

代入数据，通过计算可得卷筒临界应力Pcr2=331.11 MPa。

3)有限元法。以上对于卷筒稳定性理论计算方法基于卷筒均布载荷作用下，因此采用Ansys对卷筒进行屈曲分析，采用均布载荷的加载方式。对优化前卷筒表面施加1 MPa的均布载荷，同时对其施加边界条件，求解后得到卷筒一阶屈曲模态如图7所示，卷筒屈曲载荷因子为352.44，卷筒所受外部载荷为1 MPa，可得卷筒临界应力为352.44 MPa，理论计算卷筒临界应力为331.11 MPa，理论计算结果和有限元计算结果相差6.05%。证明有限元计算方法的准确性。

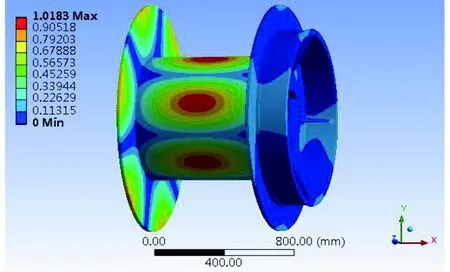
图7 卷筒一阶屈曲模态

4.2 各种稳定性方法比较

表3为各种稳定性计算方法对比，得出以下结论：①方法1为传统校核卷筒稳定性方法，通过传统方法得到的稳定性结果仍满足要求，证明卷筒壁厚的选择是合理的；②方法2和方法3得到的结果相差6.05%，证明了通过有限元法校核卷筒稳定性的可行性，为后续卷筒稳定性校核提供了新方法；③方法1得到的结果相比于方法2和方法3小很多，说明传统的稳定性校核方法过于保守，采用传统的公式设计的卷筒过于安全，是不合理的。

表3 各种稳定性计算方法对比

4.3 优化后卷筒屈曲分析

绞缆机在实际工况下，缆绳卷筒按照欧拉递减方式作用于卷筒表面，因此按欧拉递减方式对优化后卷筒施加1 MPa载荷，优化后卷筒一阶屈曲模态，如图8所示。

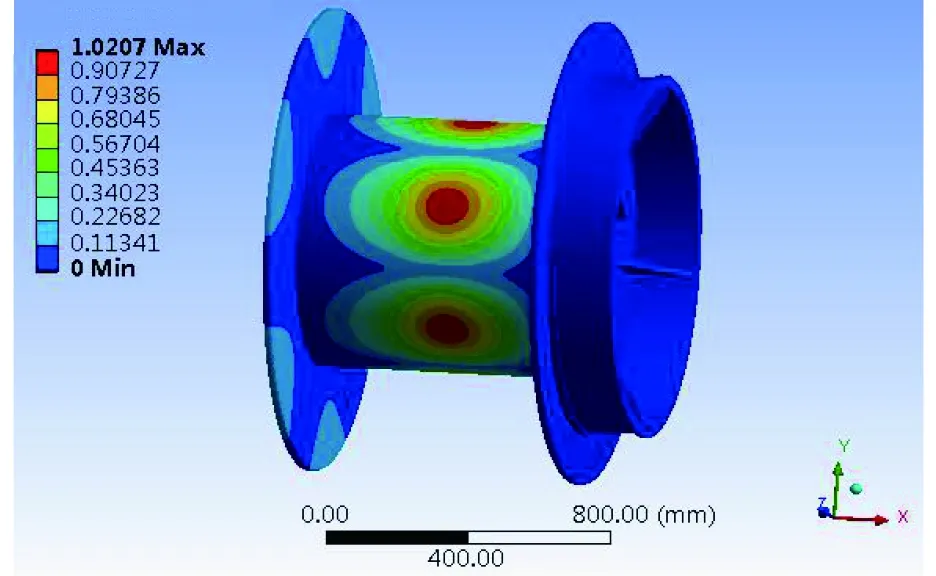
图8 优化后卷筒一阶屈曲模态

从分析结果可知，优化后绞缆机卷筒临界载荷为1 175.2 MPa，而绞缆机卷筒在实际工作工程中所受载荷不可能达到临界值，证明优化后绞缆机卷筒不仅强度满足要求，稳定性也满足要求。

5 结束语

1)绞缆机卷筒在支持负载工况下，卷筒最大应力为125.43 MPa，最大位移为0.31 mm，最大应力由出绳端逐渐向两端递减，符合欧拉递减规律。同时最大应力远小于许用应力值，存在一定的优化空间。

2)将卷筒筒壳结构改为加筋圆筒结构，在满足卷筒应力和变形的条件下，筒壳厚度由原来的35 mm降为23 mm，卷筒质量减少12.8%，轻量化效果明显。

3)通过Ansys对卷筒进行屈曲分析，与理论计算结果相差6.05%，证明了基于有限元得到的结果的准确性。对比传统的稳定性计算方法和有限元计算方法，传统稳定性计算方法过于保守。接着对优化后卷筒进行屈曲分析，结果表明，优化设计后绞缆机卷筒临界载荷为1 175.2 MPa，卷筒稳定性满足要求。