基于矢量计算的雷达监测信号处理方法

付 林，江伟伟，陆 峻

(中国船舶集团有限公司第八研究院，南京 211153)

0 引 言

数字相控阵雷达中通道间的相位不一致性对数字波束形成的波束指向及方向图副瓣电平等均会产生较大的影响。数字相控阵雷达工作时需要对通道间的相位不一致性进行补偿。通道间相位差的获取求解方法有IQ正交求解法[1]、数字相关法[2]、FFT法[3]和相位差分法[4]。在各种方法的使用过程中均需要对IQ数据进行计算求解。但是，直接编程序对IQ数据进行计算，由于PowerPC主频较低等不足，导致计算时间长，无法达到使用要求。

针对上述问题，本文提出一种基于矢量计算的雷达监测信号处理的方法，设计并实现了实时雷达监测信号处理模块。实时雷达监测信号处理模块分析并分解雷达监测信号处理流程，将其重新设计为基于矢量进行计算的计算流程，采用PowerPC矢量库，实现了高效的信号处理，可以满足实时雷达监测信号处理的要求。

1 算法描述

本文以FFT法[3]为例对算法进行理论描述和算法分解。

1.1 FFT法理论描述[3]

用FFT法求解通道之间的相位差的基本原理是：通过FFT得到两路同频信号的离散频谱，分别求出其在最大谱线处的相位值，将求得的两路信号相位值相减即可得到两路信号的相位差。

设两路信号分别为

x1(t)=A1cos(2πf0t+θ1)，

x2(t)=A2cos(2πf0t+θ2)

(1)

式中，A1、A2为信号幅度，f0为信号载频。进行离散化处理，采样频率为fs，并对信号做N点FFT，则信号载频f0可以表示为

f0=(k0+δ)·Δf

(2)

式中，k0为整数；δ为泄露误差系数，且|δ|≤0.5；Δf为频率分辨率，且Δf=fs/N。则

x1(n)=A1cos[2π(k0+δ)·n/N+θ1]，

n=0,1,…,N-1

(3)

对x1(n)进行傅里叶变换后得

k=0,1,…,N-1

(4)

X1(k)在k=k0处有最大谱线。只考虑正频率成份，则有

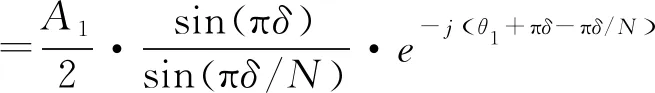
(5)

X1(k)在k=k0处的相位φ1为

φ1=θ1+πδ-πδ/N

(6)

同理，信号x2(n)的频谱X2(k)在k=k0处的相位φ2为

φ2=θ2+πδ-πδ/N

(7)

所以，两信号的相位差为

φ=θ2-θ1=φ2-φ1

(8)

1.2 矢量算法

从上述理论描述中对x1(t)进行采样后得到x1(n)，同样对x2(t)进行采样后得到x2(n)。根据式(4)需要对x1(n)和x2(n)进行傅里叶变换。传统方法需要通过for语句对IQ进行复合变换为复数，即

x1C(i)=x1I(i)+j·x1Q(i),i=1,…,n

(9)

x2C(i)=x2I(i)+j·x2Q(i),i=1,…,n

(10)

而采用PowerPC矢量库后，设计矢量计算方法则为

(11)

(12)

随后的傅里叶变换采用FFT算法：

(13)

(14)

式(5)中需要找到X1(k)和X2(k)的最大值，同样需要使用循环语句，即

X(i)A=|X(i)|,i=1,…,n

(15)

kMax=k, {X(k)A=Max[X(n)A]}

(16)

设计矢量计算方法则为

(17)

(18)

同样的，根据式(6)、(7)可以得到φ1、φ2，利用式(8)得到相位差φ。

2 仿真分析

以两个通道为例，在输入相同的正弦单频点测试信号时设两通道输出信号的初相差为10°，分别加复数形式的高斯白噪声，采样频率fs=200 MHz，载频f0=80 MHz，进行了100次通道测量计算。分别采用矢量算法和传统循环算法时仿真结果如表1所示。

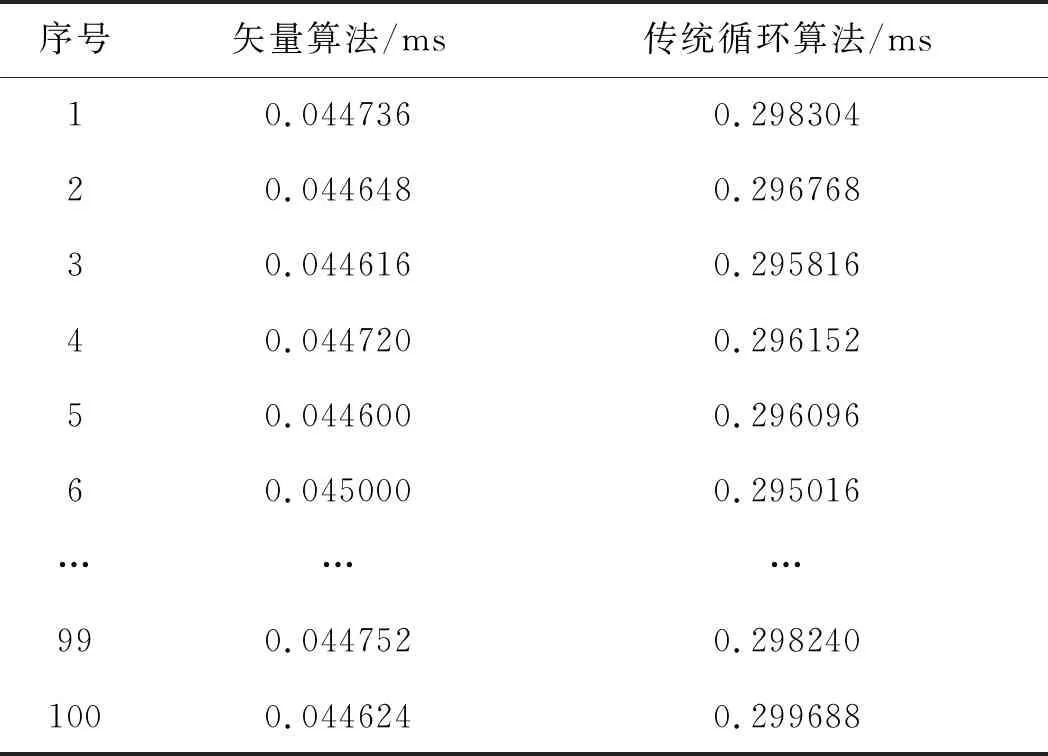
表1 通道相位差测量计算时间对比

由仿真结果可见，采用矢量算法将算法效率提高一个数量级，其单通道计算时间均为T<0.045 ms，当通道数为80时计算所有通道所需时间小于3.6 ms，再对所有50个载频进行计算。计算所需时间小于180 ms，远小于监测流程所需的工作时间，可以满足工程实践要求。

3 结束语

现代雷达信号处理中大量采用PowerPC平台。PowerPC平台由于其CPU主频低等特点导致传统常规的计算方法效率低，无法满足雷达信号处理的实时性要求。本文提出的基于PowerPC矢量库的矢量算法，充分利用CPU的流水线性能，极大地提高了计算性能，满足了工程实践中信号处理对实时性的要求，具有工程实用价值。