脉冲涡流检测激励参数和激励线圈参数的优化设计

宫 昊,郝宪锋,王安泉,孙伟峰,戴永寿

(1.中国石油大学(华东) 信息与控制工程学院， 青岛 266580；2.中国石化股份胜利油田分公司 技术检测中心， 东营 257000)

腐蚀造成的壁厚减薄是承压设备失效破坏的主要原因之一，为了保障承压设备的运行安全，需定期对其剩余壁厚进行检测[1-2]。脉冲涡流检测具有穿透能力强、检测信号包含更多缺陷信息的特点，被广泛应用于承压设备的缺陷检测中[3]。检测过程中，脉冲激励参数和激励线圈参数的不同会对检测结果产生较大的影响。为了研究参数变化对检测结果的影响，徐志远等[3]研究了激励参数和试件电磁参数对检测信号的影响；张辉等[4]研究了矩形传感器尺寸、激励脉冲频率及占空比对检测结果的影响，得出需要根据被测试件的厚度来设计激励频率和占空比的结论；周德强等[5]对传感器几何参数和激励频率进行了优化设计，给出了试验中所用的最佳频率；朱红运等[6]研究了激励电流对检测的影响规律。为了提高涡流检测的灵敏度和分辨率，笔者通过仿真试验研究了脉冲激励参数及激励线圈参数对铁磁性试件壁厚检测灵敏度和分辨率的影响，确定了脉冲激励参数和激励线圈参数；最后以铁磁性阶梯试件为检测对象，对仿真结果进行了验证。

1 脉冲涡流检测的基本原理

将具有一定幅值、频率和占空比的脉冲信号加到激励线圈两端，由法拉第电磁感应定律得知，在脉冲信号的跳变沿处,激励线圈周围会产生变化的磁场B1。当激励线圈靠近被测试件时，激励线圈周围变化的磁场会在试件中感应出变化的涡流，涡流的变化又会产生另一个变化的磁场B2。将检测线圈磁场的变化转换为随时间变化的电压信号，电压信号中包含着有关试件厚度的信息，提取检测电压信号中的某些特征就能实现壁厚的反演[7]。脉冲涡流测厚原理示意如图1所示(图中r0,r1,h分别为激励线圈的内半径、外半径和高度)。

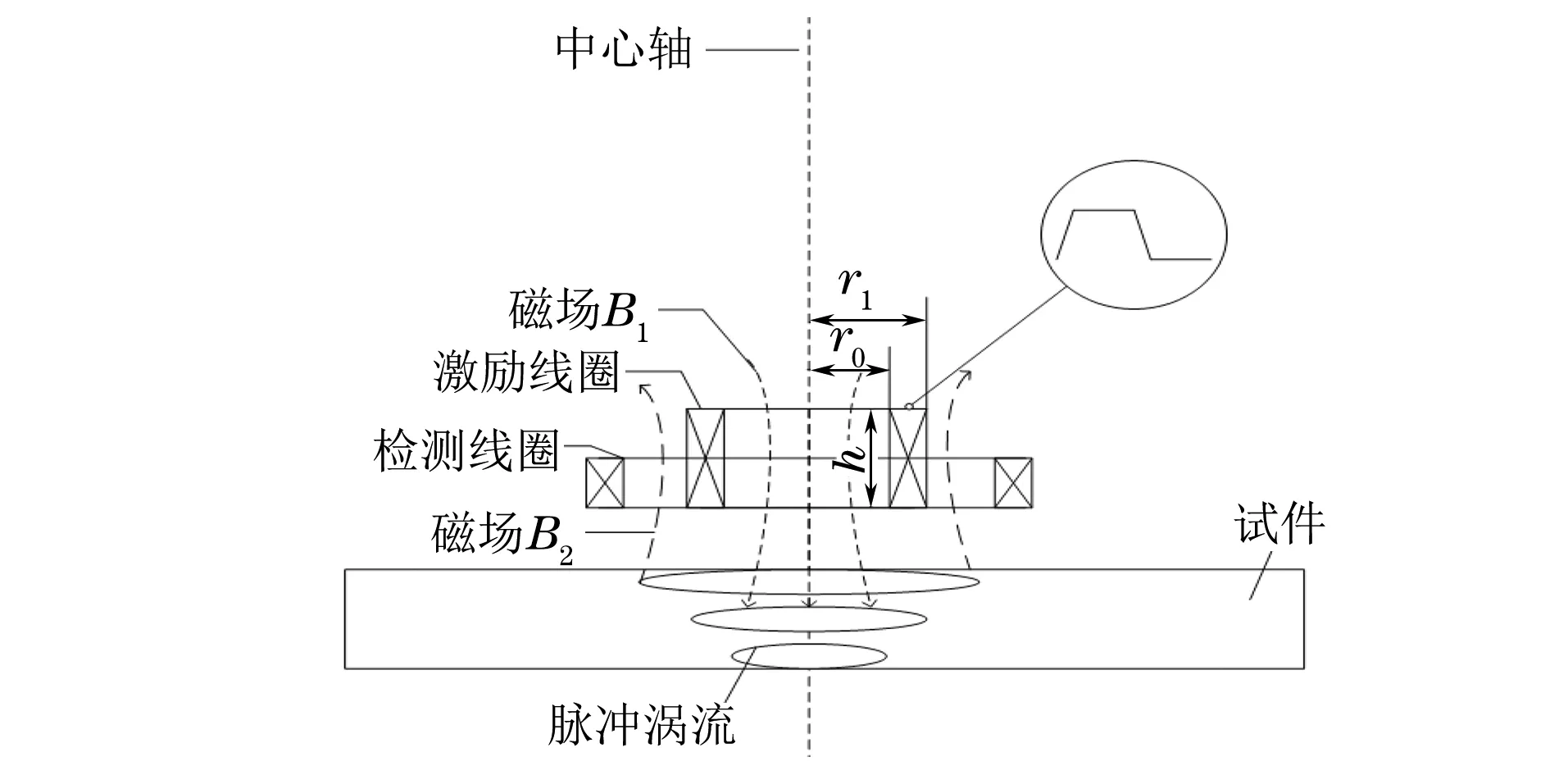
图1 脉冲涡流测厚原理示意

2 脉冲涡流测厚模型及仿真试验内容

2.1 脉冲涡流测厚模型

为了研究检测参数对检测结果的影响，利用COMSOL Multiphysics仿真软件建立了脉冲涡流测厚模型。由于模型具有对称性，同时为了减小计算量，将三维仿真模型转化为二维仿真模型(见图2)。模型中激励线圈和检测线圈均是同轴的空心圆柱形结构，激励线圈在内,检测线圈在外，线圈材料设置为铜。为了计算方便，以厚度均匀的钢板替代管道作为被测试件，钢板的电导率设置为7.1 MS·m-1，相对磁导率设置为250。

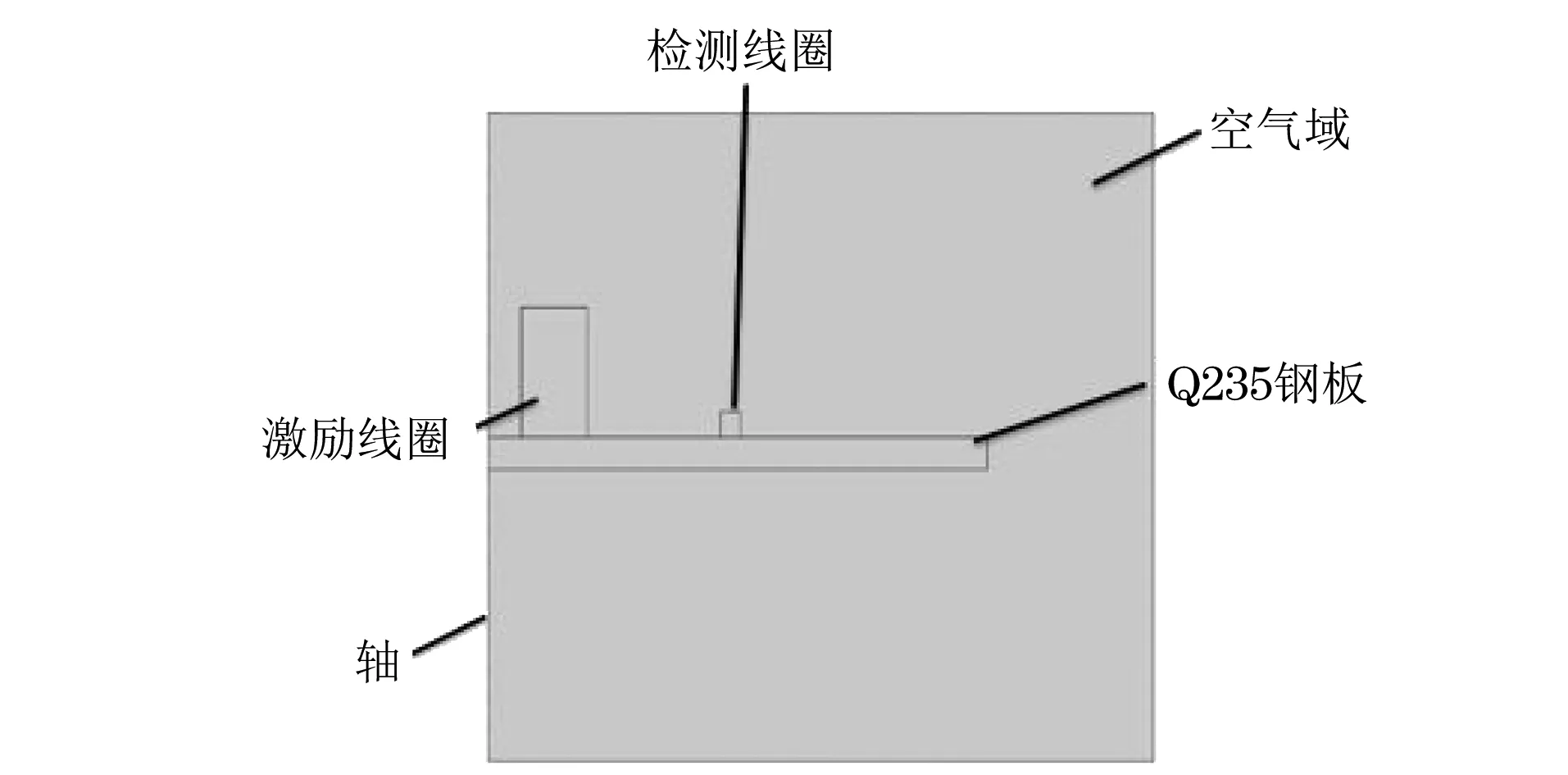
图2 脉冲涡流测厚二维仿真模型

2.2 仿真试验内容

通过图1可以看出，对脉冲涡流检测结果造成影响的主要参数有脉冲激励参数、激励线圈参数及检测线圈参数，但检测线圈参数相较于脉冲激励参数和激励线圈参数,对检测灵敏度和分辨率的影响较小。仿真过程中保持检测线圈的参数不变，设置检测线圈的内半径为72 mm,外半径为76 mm,高度为4 mm,匝数为800匝。脉冲激励及激励线圈的主要参数如表1所示。

表1 脉冲激励及激励线圈的主要参数

以差分电压信号峰值为特征来研究参数变化对检测灵敏度和分辨率的影响。差分电压信号峰值的定义如式(1)所示。

ΔV=max(Vnodefect-Vdefect)

(1)

式中：Vnodefect为无缺陷处的检测电压信号，此时的信号为参考信号;Vdefect为缺陷处的检测电压信号,此时的信号为缺陷信号;ΔV为参考信号减去缺陷信号的最大值[1]，ΔV越大，则检测的灵敏度越高，不同厚度对应的ΔV变化量越大，则检测的分辨率越高。

仿真时被测试件的厚度设置为8, 11, 14, 17, 20 mm，其中最大厚度20 mm用来模拟无缺陷的情况，8,11,14,17 mm厚度用来模拟壁厚减薄的情况。脉冲涡流测厚仿真试验流程如图3所示。

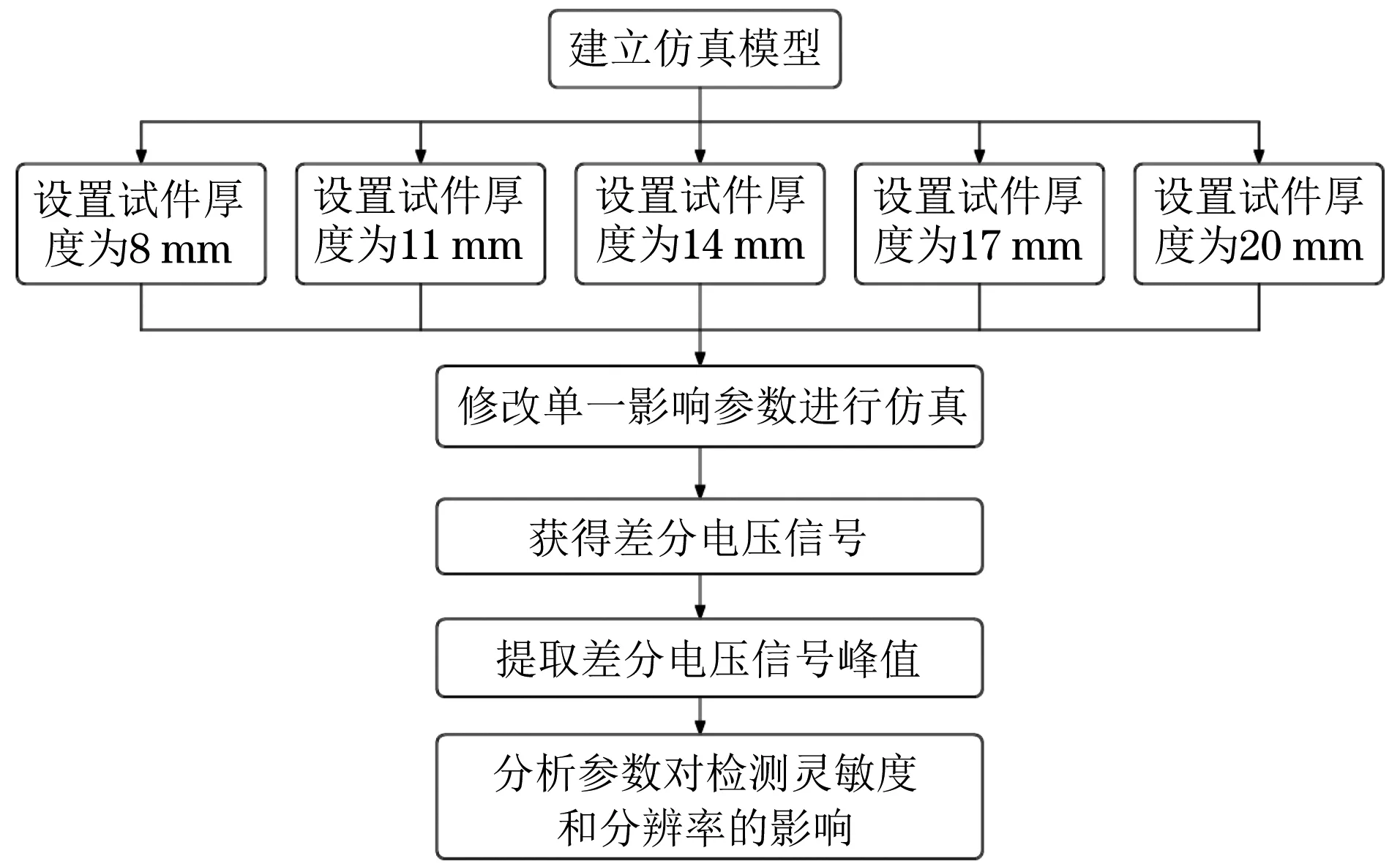
图3 脉冲涡流测厚仿真试验流程

3 参数的仿真优化设计

3.1 脉冲激励参数的优化设计

在研究脉冲激励参数对检测的影响时，保持激励线圈和检测线圈的参数不变。设置激励线圈的内半径为10 mm,外半径为30 mm,高度为40 mm,匝数为400匝。检测线圈的内半径为72 mm,外半径为76 mm,高度为4 mm,匝数为800匝。限于篇幅，在此仅详细介绍脉冲激励电压幅值的优化过程。

保持激励电压的其他参数不变，仅改变电压幅值进行仿真试验。电压幅值设置为20,25,30,35 V，设置频率为1 Hz,占空比为50%,边沿时间为1 ms。在不同的电压幅值下，8 mm试件厚度的差分电压信号如图4所示，激励电压幅值与差分电压信号峰值关系曲线如图5所示，不同激励电压幅值下不同厚度对应的差分电压信号峰值如表2所示。

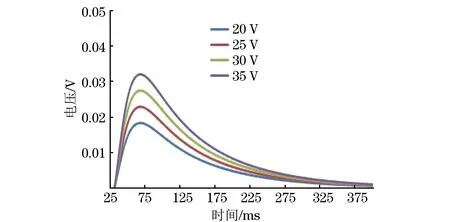
图4 不同电压幅值下，8 mm试件厚度的差分电压信号

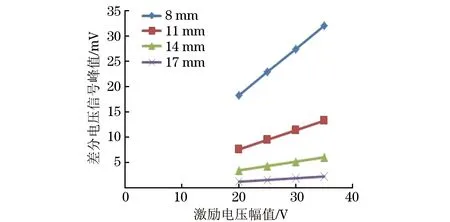
图5 激励电压幅值与差分电压信号峰值关系曲线(仿真)

将表2中的数据绘制在同一个直角坐标系中，得到的激励电压幅值与差分电压信号峰值关系曲线如图5所示。从图5可以看出，随着电压幅值的增大，同一厚度对应的差分电压信号峰值都增大，不同厚度之间的差分电压信号峰值的变化量也增大，即随着激励电压幅值的增大，检测的灵敏度和分辨率均得到了提高。但在实际检测过程中，激励电压幅值越大，则产生的热量越高，容易损坏激励线圈，综合考虑，选定激励电压幅值为30 V。

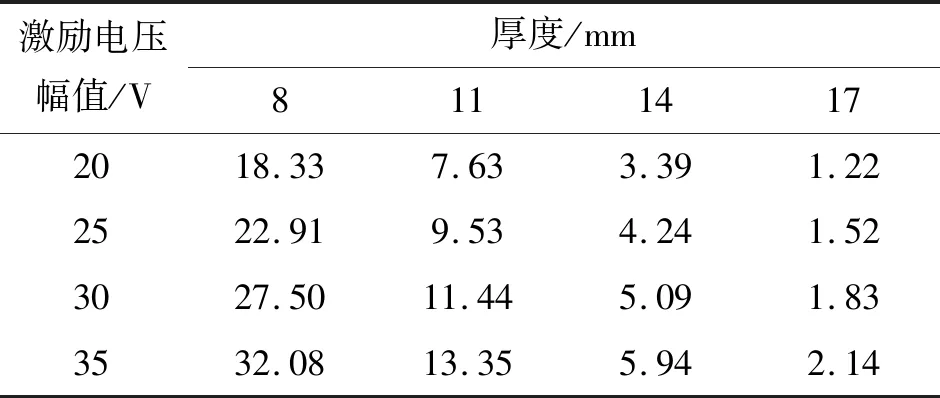
表2 不同激励电压幅值下,不同试件厚度对应的差分电压信号峰值 mV

激励电压频率与差分电压信号峰值关系曲线如图6所示。从图6可以看出,随着电压频率的增大，同一厚度对应的差分电压信号峰值都减小，不同厚度之间的差分电压信号峰值的变化量也减小，即随着激励电压频率的增大，检测的灵敏度和分辨率均降低。由涡流渗透深度公式[8](2)得知,激励电压频率越小则渗透深度越大，检测的灵敏度和分辨率越高，这与仿真结果相符。

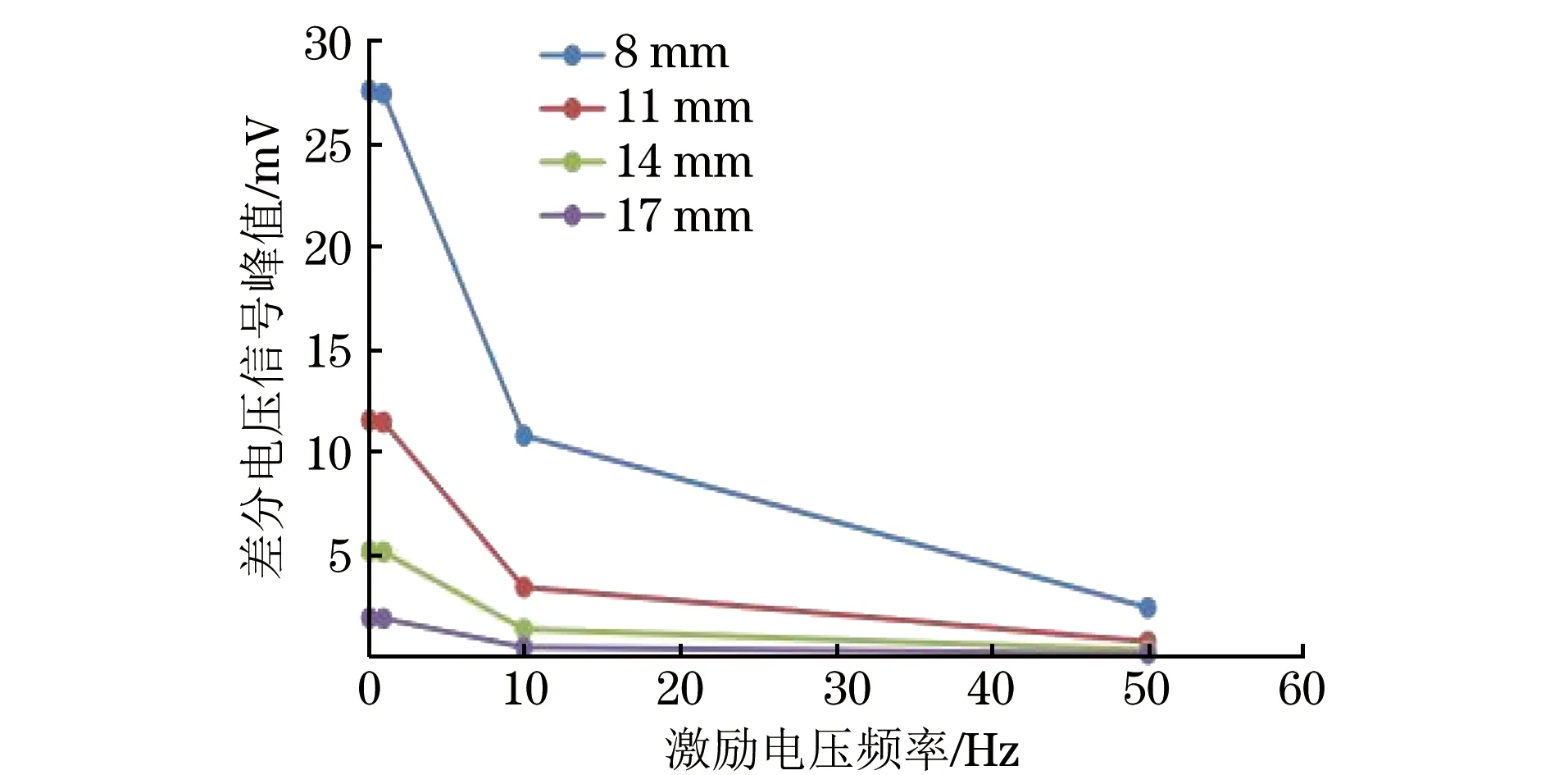
图6 激励电压频率与差分电压信号峰值关系曲线(仿真)

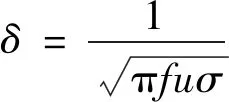
(2)

式中：f为激励电压频率;μ为被测试件的磁导率;σ为被测试件的电导率;δ为涡流渗透深度。

此外，由于在0.1 Hz和1 Hz条件下，检测的灵敏度和分辨率相差无几，综合考虑，选定激励电压频率为1 Hz。激励电压占空比与差分电压信号峰值关系曲线如图7所示。从图7中可以看出，随着电压占空比的增大，同一厚度对应的差分电压信号峰值不改变，即检测的灵敏度和分辨率不受激励电压占空比的影响。但占空比过小会导致涡流不能有效扩散到试件下表面，从而检测信号中不包含有关试件厚度的信息，而占空比过大又会导致产生的热量更高。因此，综合考虑，选定激励电压的占空比为50%。

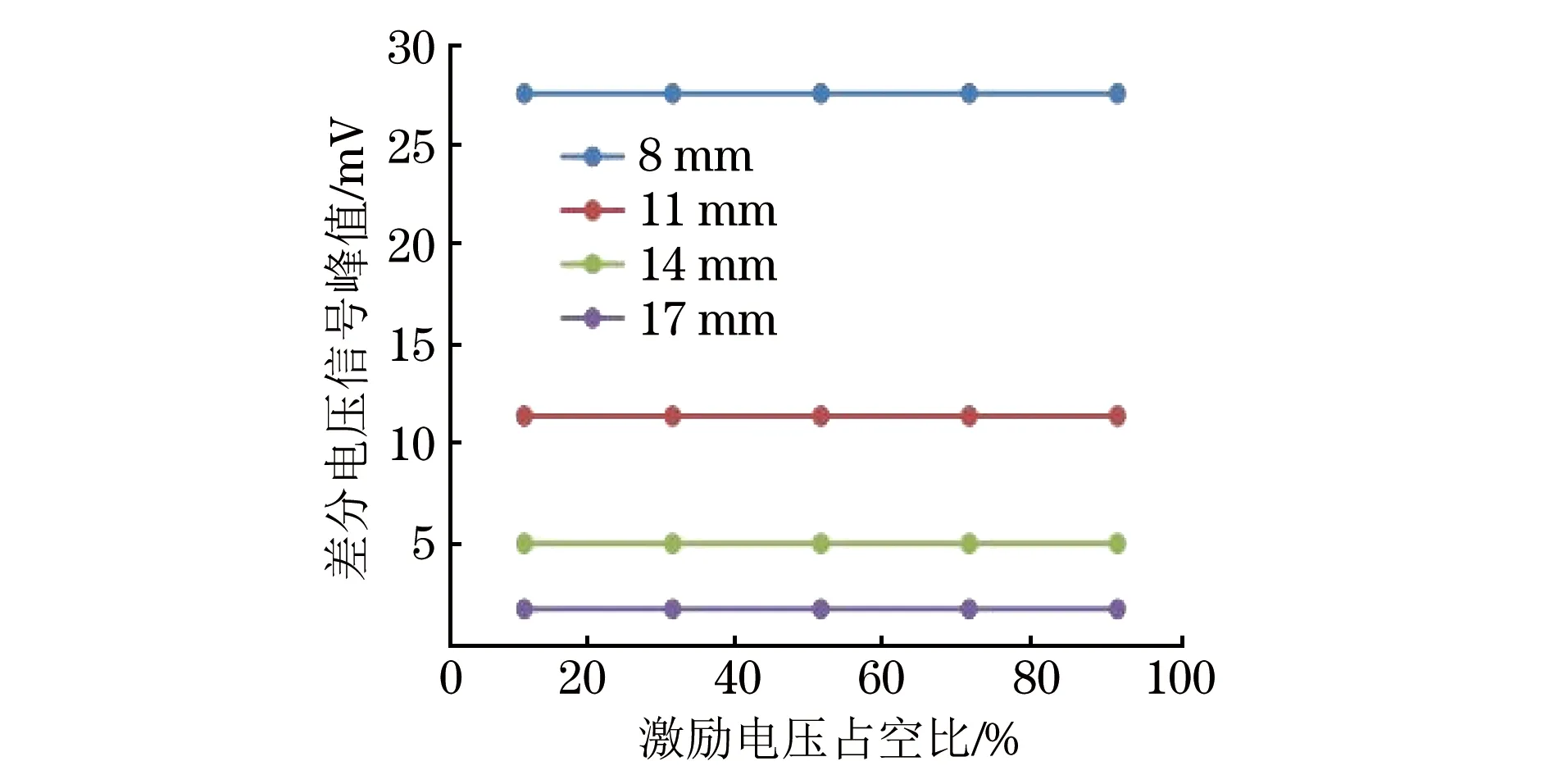
图7 激励电压占空比与差分电压信号峰值关系曲线(仿真)

3.2 激励线圈参数的优化设计

激励线圈的参数设计是脉冲涡流检测系统设计中的一个重要环节，激励线圈的参数直接影响被测试件中涡流的大小及扩散情况。通过研究发现，小尺寸探头适用于检测小壁厚，大尺寸探头适用于检测大壁厚[1]。通过研究激励线圈内半径、外半径、高度及匝数对检测灵敏度和分辨率的影响，对激励线圈的参数给出了选定依据。在研究激励线圈参数对检测的影响时，保持脉冲激励电压参数不变，设置电压幅值为30 V，占空比为50%，频率为1 Hz，边沿时间为1 ms。

保持激励线圈的其他参数不变，仅改变激励线圈内半径进行仿真试验。设置激励线圈内半径为5,10,15,20,25 mm，外半径为30 mm,高度为40 mm,匝数为400匝。在不同的激励线圈内半径下，8 mm试件厚度的差分电压信号如图8所示，不同激励线圈内半径下,不同厚度对应的差分电压信号峰值如表3所示。

图8 不同激励线圈内半径下，8 mm试件厚度的差分电压信号

将表3中的数据绘制在同一个直角坐标系中，得到激励线圈内半径与差分电压信号峰值关系曲线如图9所示。从图9可以看出，随着激励线圈内半径的增大，同一试件厚度对应的差分电压信号峰值略有增大，不同厚度之间的差分电压信号峰值的变化量也略有增大，即随着激励线圈内半径的增大，检测的灵敏度和分辨率都略有提高。然而，激励线圈内半径过大时，不能有效检测小范围腐蚀。综合考虑，选定激励线圈内半径为10 mm。

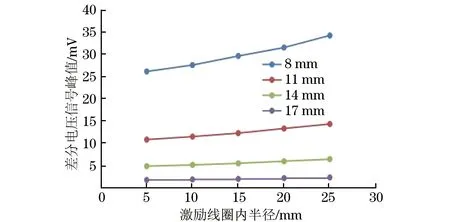
图9 激励线圈内半径与差分电压信号峰值关系曲线

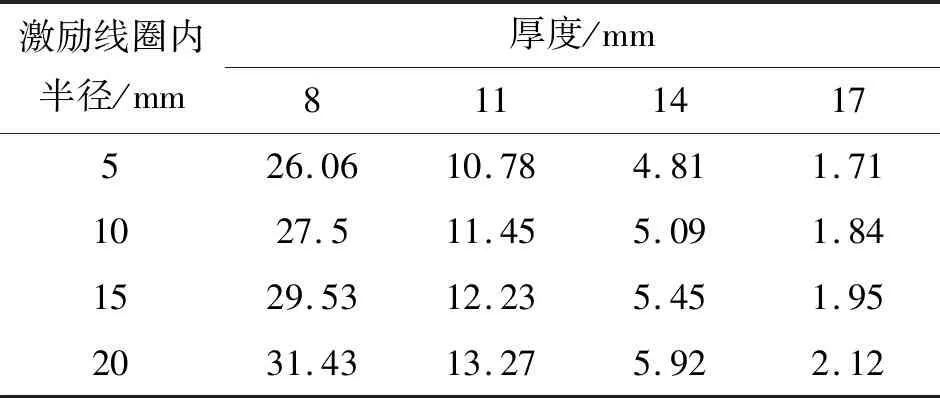
表3 不同激励线圈内半径下，不同试件厚度对应的差分电压信号峰值 mV

激励线圈外半径与差分电压信号峰值关系曲线如图10所示。从图10可以看出，随着激励线圈外半径的增大，同一厚度对应的差分电压信号峰值略有增大，不同厚度之间的差分电压信号峰值的变化量也增大，即随着激励线圈外半径的增大，检测灵敏度和分辨率都有所提高。然而，激励线圈外半径过大时，不能有效检测小范围腐蚀。综合考虑，选定激励线圈外半径为30 mm。

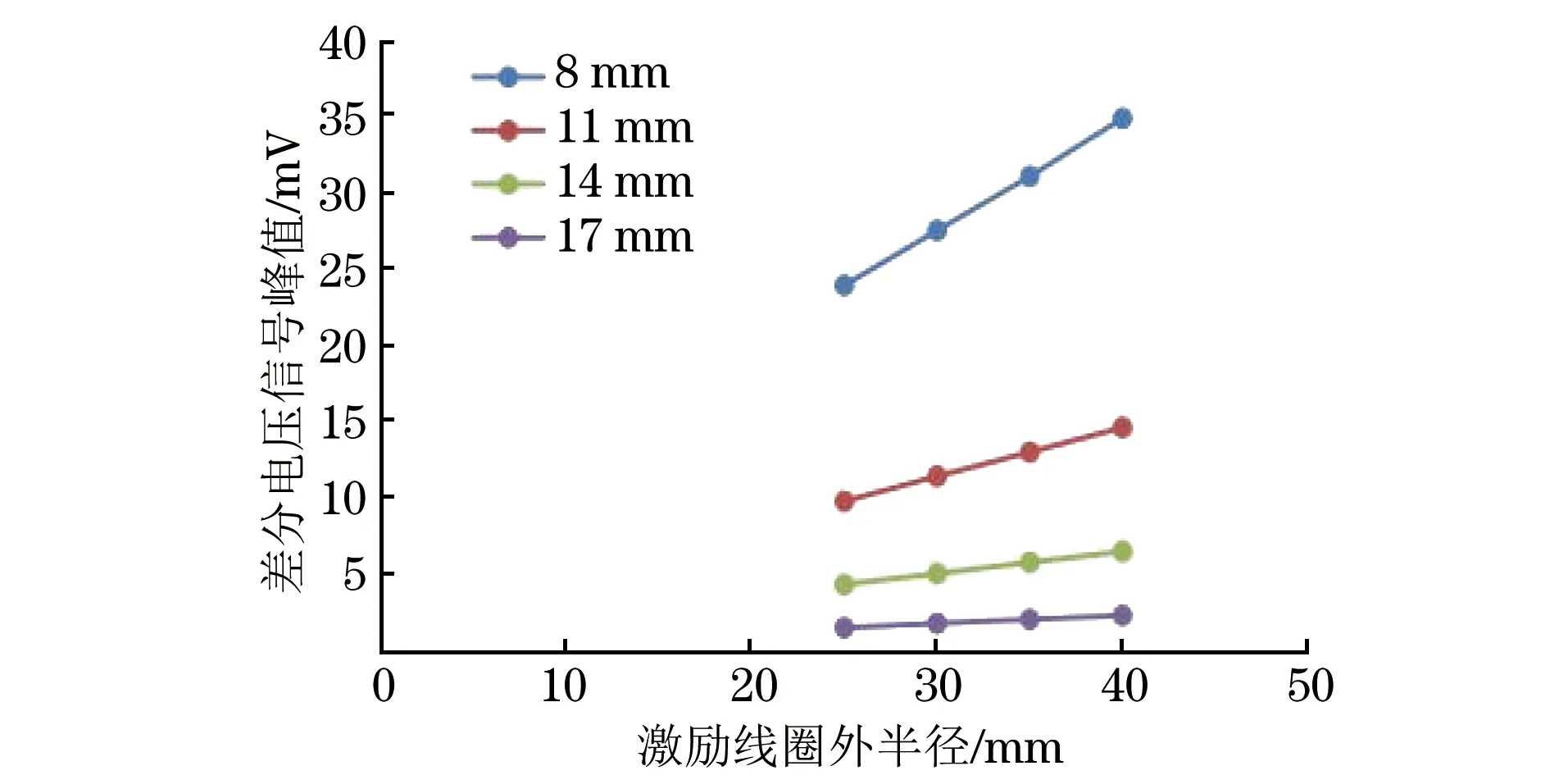
图10 激励线圈外半径与差分电压信号峰值关系曲线

激励线圈高度与差分电压信号峰值关系曲线如图11所示。从图11可以看出，随着激励线圈高度的增大，同一厚度对应的差分电压信号峰值减小，不同厚度之间的差分电压信号峰值的变化量也减小，即随着激励线圈高度的增大，检测灵敏度和分辨率都降低。然而，激励线圈的高度过小时，不能有效检测较大厚度的试件。结合现场的壁厚检测需求，综合考虑，选定激励线圈高度为40 mm。

图11 激励线圈高度与差分电压信号峰值关系曲线

激励线圈匝数与差分电压信号峰值关系曲线如图12所示。从图12可以看出，随着激励线圈匝数的增多，同一厚度对应的差分电压信号峰值略微减小，不同厚度之间的差分电压信号峰值的变化量也略微减小，即随着激励线圈匝数的增多，检测灵敏度和分辨率的变化不太明显。然而，匝数的多少会影响磁场强度，进而影响壁厚的检测范围，综合考虑，选定激励线圈匝数为400匝。

图12 激励线圈匝数与差分电压信号峰值关系曲线

3.3 探头厚度检测范围的确定

在前两小节介绍了脉冲激励参数和激励线圈参数对检测的影响，确定了脉冲激励参数和激励线圈参数。激励线圈电压幅值为30 V，频率为1 Hz，占空比为50%，边沿时间为1 ms，激励线圈内半径为10 mm，外半径为30 mm，高度为40 mm，匝数为400匝;检测线圈的内半径为72 mm，外半径为76 mm,高度为4 mm，匝数为800匝。为了确定在该参数下的有效厚度检测范围，以单对数坐标系下信号后期斜率(脉冲涡流检测电压信号曲线的后期在单对数坐标系中趋于直线，该直线的斜率为信号后期斜率)为特征[9]，通过仿真试验确定了有效厚度检测范围。

仿真时被测试件的厚度为1.5～45 mm，单对数坐标系下的检测电压信号如图13所示。通过提取信号后期斜率并建立其与厚度之间的关系发现，试件厚度为4～24 mm的信号后期斜率与厚度之间呈现较好的幂函数关系，拟合曲线如图14所示。斜率与厚度之间的关系如式(3)所示。

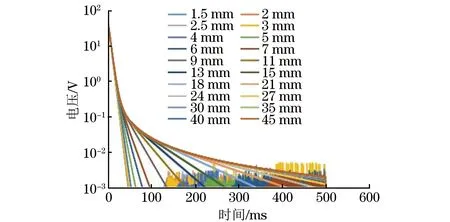
图13 单对数坐标系下的检测电压信号(仿真)

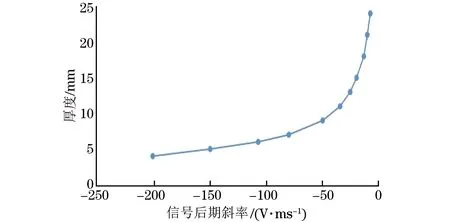
图14 信号斜率与被测试件厚度拟合曲线(仿真)

y=71.71(-x)-0.53

(3)

关系式的确定系数为0.999 1。通过仿真试验及数据分析可以得出，在该参数条件下的有效厚度检测范围为4～24 mm。

4 测试件试验及结果分析

试验系统包括自研发的脉冲激励源、Q235材料的阶梯板、探头、示波器及PC机，脉冲激励参数及探头参数与仿真试验参数相同。首先以9,11,13,15,18 mm厚度的测试件进行试验来验证脉冲激励参数仿真优化结果的正确性，试验结果如图15～17所示。

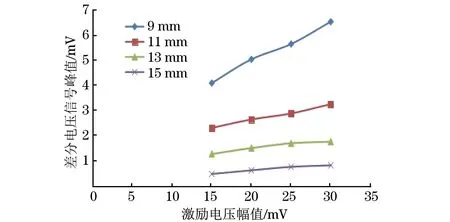
图15 激励电压幅值与差分电压信号峰值关系曲线(验证试验)

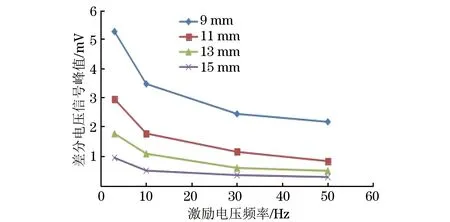
图16 激励电压频率与差分电压信号峰值关系曲线(验证曲线)

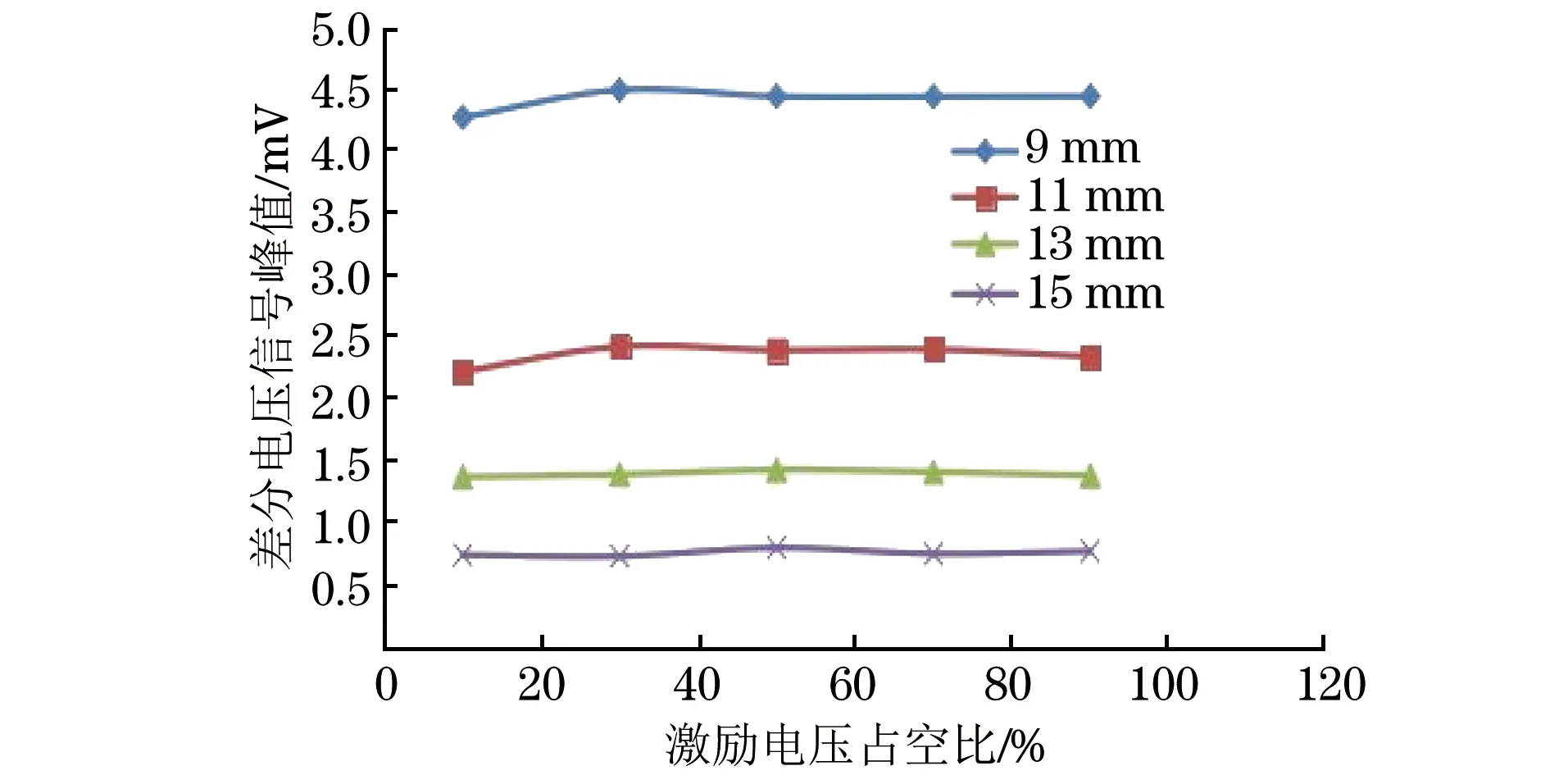
图17 激励电压占空比与差分电压信号峰值关系曲线(验证试验)

从图15～17可以看出，参数变化对检测的影响规律与仿真试验结果相同，验证了仿真结果的正确性。

然后验证探头的厚度检测范围，将采集的检测电压信号进行滤波处理及单对数转换后，得到的电压信号如图18所示。通过提取信号后期斜率并建立其与厚度之间的关系发现，厚度为7～24 mm的斜率与厚度之间呈现较好的幂函数关系，拟合曲线如图19所示。斜率与厚度之间的关系式如式(4)所示，关系式的确定系数为0.954 5。通过测试件试验及数据分析可以得出

图18 单对数坐标系下的检测电压信号(验证试验)

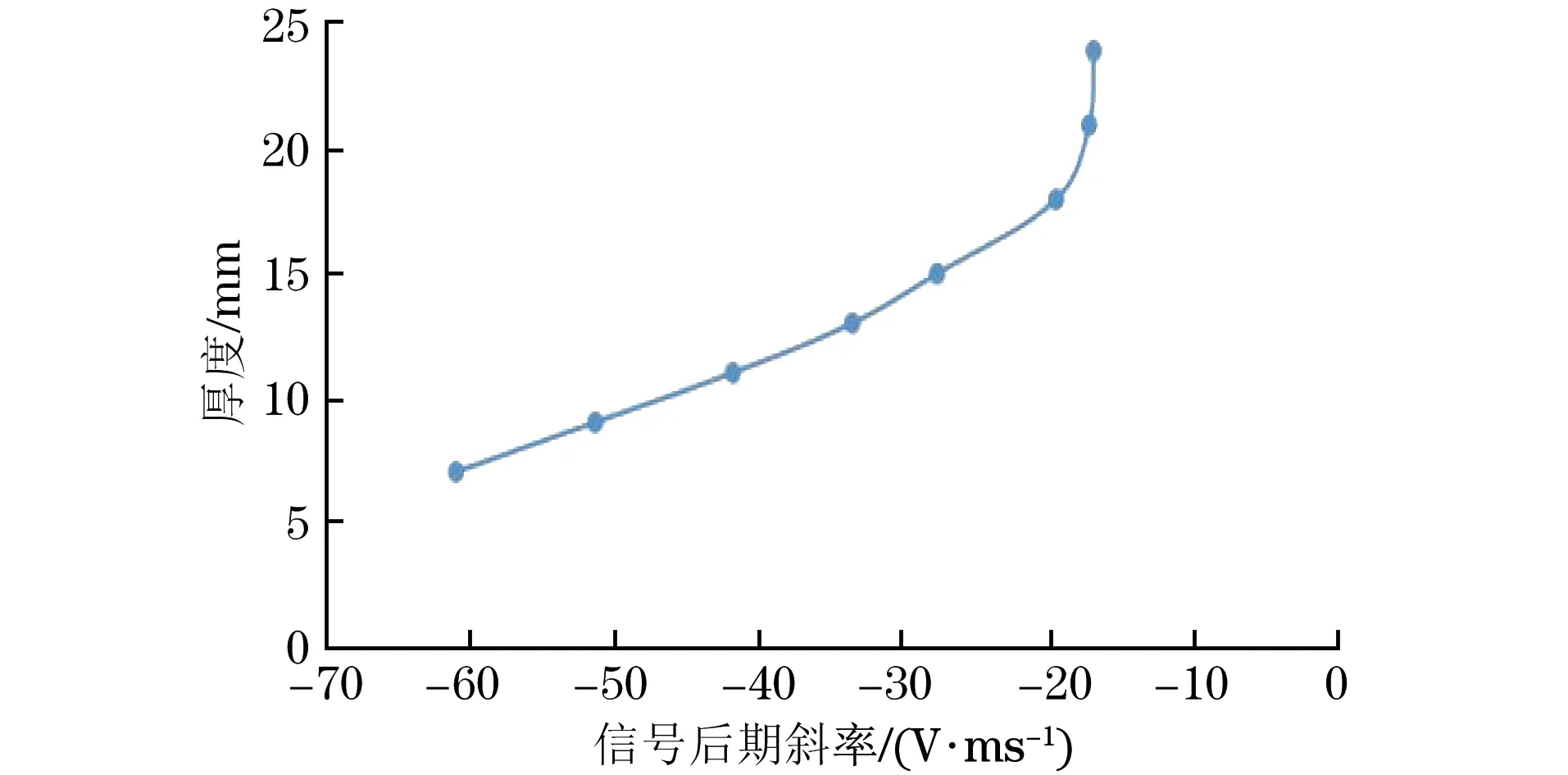
图19 信号斜率与被测试件厚度关系曲线(验证试验)

y=124.4(-x)-0.661

(4)

使用该探头能够有效检测7～24 mm厚度的试件。由于绕制的探头尺寸存在一定偏差，厚度检测范围较仿真结果略有不同。

5 结语

(1) 激励电压幅值、激励线圈内半径及激励线圈外半径越大，检测灵敏度和分辨率越高;激励电压频率、激励线圈高度及激励线圈匝数越大，则检测灵敏度和分辨率越低;激励电压占空比的变化不影响检测的灵敏度和分辨率。

(2) 激励电压幅值、激励电压频率、激励线圈外半径及激励线圈高度对检测灵敏度和分辨率的影响较大，激励电压占空比、激励线圈内半径及激励线圈匝数对检测灵敏度和分辨率的影响较小。

(3) 使用所设计的参数能够有效检测7～24 mm厚度的试件。