基于粒子群优化的超声共振谱法测量材料弹性常数

沈 飞，樊 璠，王 蕊，张 强，牛海军

(北京航空航天大学 生物与医学工程学院，北京 100191)

超声共振谱法(Resonant Ultrasound Spectroscopy, RUS)是20世纪90年代发展起来的一种材料力学特性测量方法，被物理学家认为是测量高Q值(品质因数)固体材料弹性系数的最准确方法[1-2]。其基本原理是运用超声激励样本使其产生自由振动，再根据测得的多个固有共振频率，利用反演方法计算材料的弹性系数[2-3]。方法的独特之处在于可用于尺寸极小(小于1 mm)的样本的无损检测，一次试验就能估计样本的全部弹性系数和力学参数，且具有可重复性[1]。

RUS方法求取弹性常数的过程一般转化为非线性最小二乘问题，利用梯度优化(如Levenberg-Marquardt，LM方法)对问题进行求解[1-4]。但是该方法对于高阻尼材料(Q值较低，如岩石材料、生物硬组织等)弹性常数的估计存在缺陷，主要原因是这类材料的谱线平缓、共振频率求取困难。尽管一些研究者结合线性预测法提出了平缓共振谱线中共振频率的提取技术，但是低Q值材料的试验共振频率丢失现象仍旧无法避免，这直接导致了试验共振频率与理论共振频率的配对困难，也增加了优化过程的难度[4-5]。这对弹性常数初始值的设置提出了要求，偏差稍大就会导致算法无法收敛，弹性常数计算无效。

粒子群优化是一种基于数量的进化算法，具有优良的全局寻优能力，被广泛应用于动态优化、信号处理等领域[6]。为了获得弹性常数的点估计，笔者提出了基于粒子群优化算法的RUS求解方案，可快速实现宽泛弹性常数初值设置下的弹性常数估计；并利用低Q值骨模拟材料试验进行了验证。

1 检测方法

RUS方法包括3个步骤：① 利用超声扫频试验获得材料的共振谱线；② 使用线性预测技术从共振谱线中提取共振频率；③ 不断调整弹性常数Cij，直到计算得到的共振频率fcal与试验提取的共振频率fexp相一致(见图1，图中M和K分别为样本的质量矩阵和刚度矩阵,α为共振模态，ω为角频率)。

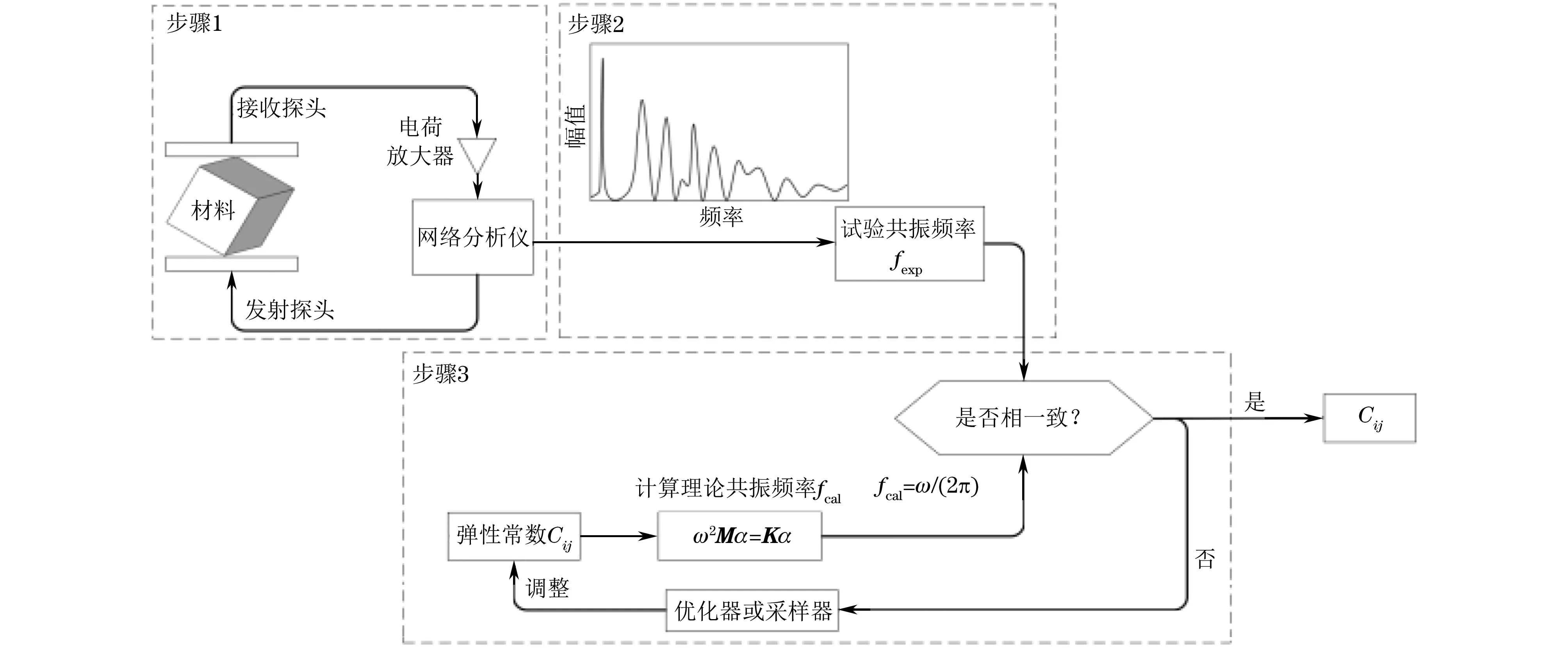
图1 超声共振谱方法流程图

1.1 理论共振频率计算与一致性准则

三维固体材料在零应力边界条件下，其共振频率由形状、密度以及弹性常数决定。一般情况下，固体的形状和密度易于测量，RUS技术通常采用Rayleigh-Ritz(瑞利-里茨)法获取理论共振频率f与弹性常数的关系。

(2πf)2Mα=Kα

(1)

已知弹性常数Cij，f以及相应的共振模态α可以通过求解式(1)实现。

但已知共振频率f无法直接反算弹性常数Cij，因此基于逆问题理论对问题建模。定义弹性常数C的后验概率密度函数，如式(2)所示。

(2)

式中：ρ为理论共振模态与试验共振模态的配对关系，表示为离散向量的形式，如ρ=[1,3,6],说明试验测量的前3个共振频率分别与理论共振频率的第1,3,6个对应;p为概率。

C与ρ的先验相互独立，似然函数p(f|C,ρ)表示试验共振频率与弹性常数和配对的关系，可以使用多元高斯分布来表示[7]。这里假设C的先验服从多元对数高斯分布，进一步假设ρ的先验如式(3)所示。

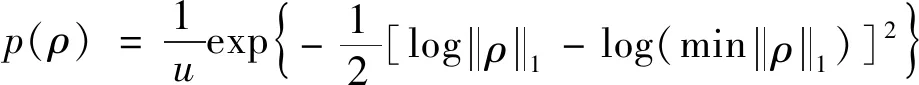
(3)

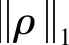
由于高阶共振频率一般较集中，故配对低阶共振频率比配对高阶共振频率更加可信，即ρ中元素应倾向于取小值。根据逆问题的贝叶斯理论，后验概率密度最大值所对应的C便是材料弹性常数的最优点估计。

最大化式(2)的后验概率密度，采用分步计算的方式，首先对后验概率密度函数取负对数，估计理论共振频率与试验共振频率的最优配对ρ，即ρ表示为C的函数，再优化弹性常数C。

考虑到ρ的变动对似然函数p(f|C,ρ)取值的影响要远大于其对先验函数p(ρ)的影响，故估计最优配对ρ近似于最小化-logp(f|C,ρ)。显然这是一个线性和指派问题，可采用匈牙利算法进行求解[8]。弹性常数C的优化则可以借助全局优化器粒子群算法实现。

1.2 粒子群优化估计弹性常数

考虑到模型的高度非线性，以及负对数后验概率密度函数具有众多极值点，采用粒子群优化的方法寻找全局最小值。粒子群优化(PSO)是一种基于数量的随机优化算法，函数上每一个可能的采样点称为一个粒子，基于有限粒子间的信息交流来寻找问题的最优解。为了加速粒子的探索能力，在原始PSO中引入了梯度下降和变异操作(见图2)。

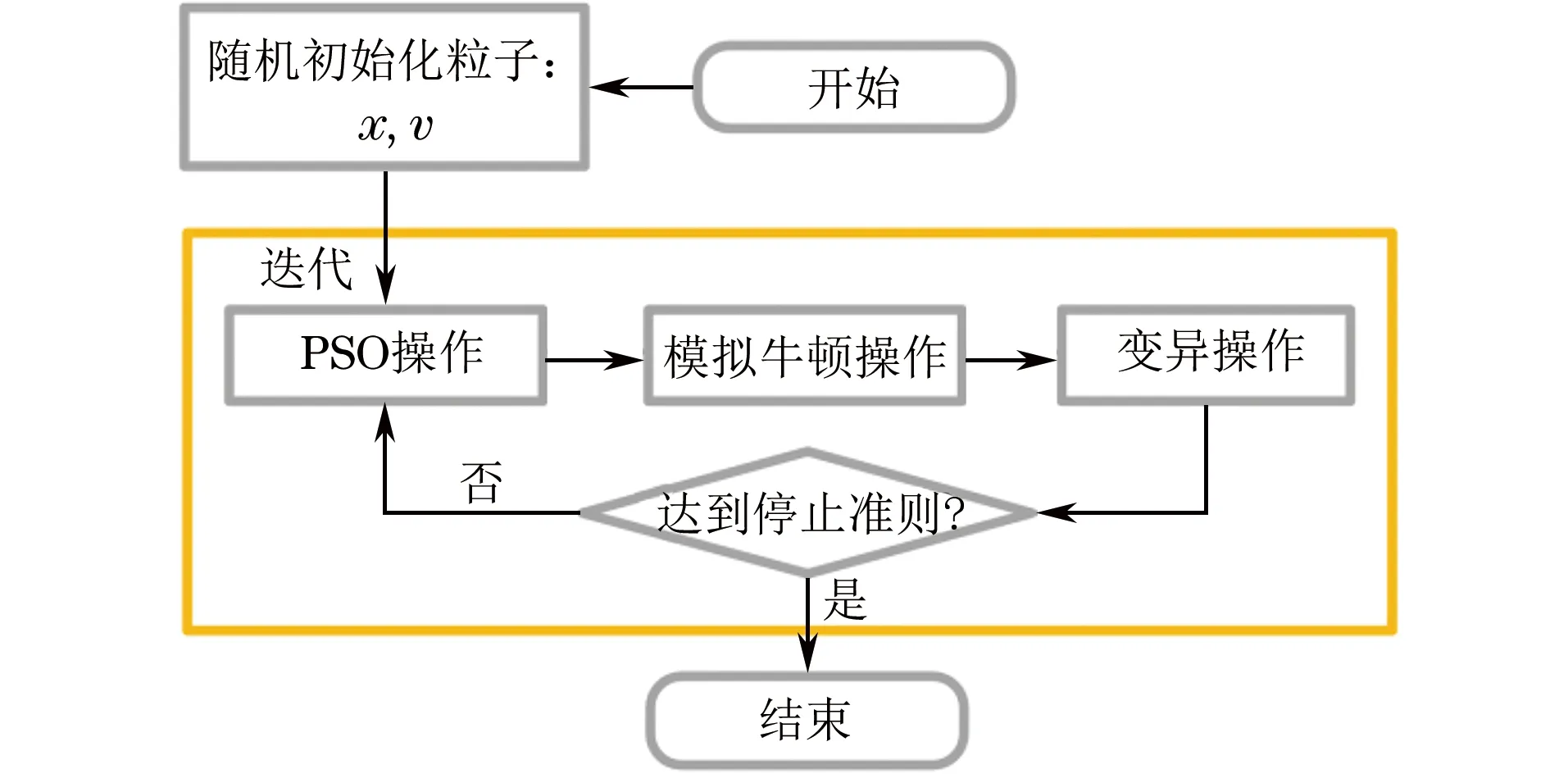
图2 具有梯度和变异操作的粒子群优化算法流程图

梯度下降：对后验概率密度函数计算一阶导数和二阶导数，并将模拟牛顿法应用到迭代算法中。尽管这一方法有助于提高粒子的局部寻优能力，但这是以计算导数为代价的，因此会增加计算开销。

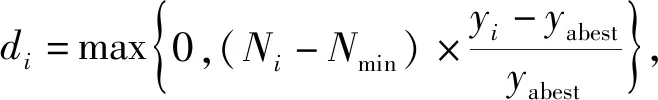
每次迭代时，计算最优粒子所对应的理论共振频率与试验共振频率的相对均方误差，当均方误差小于一定值时(试验中设置为0.5%)停止迭代。

2 试验过程

2.1 试验系统以及试验共振频率的提取

为了验证算法在实际材料测量上的有效性，选择了一种皮质骨模拟材料(短纤维环氧树脂，横观各向同性，SAWBONES®)，Q值约为25，将材料切割、打磨成标准长方体，骨样品的尺寸(长×宽×高)为5.84 mm×6.74 mm×6.64 mm,质量为428.6 mg。样品的对角被夹持在两个超声探头中间，接收探头端连接电荷放大器将接收到的振动信号放大后输入网络分析仪，并上传到计算机,试验系统框图如图3所示。计算机对共振谱线进行处理，提取试验共振频率。共振频率提取细节参见文献[9]。图4展示了测量到的共振谱图以及通过线性预测法获得的试验共振频率。

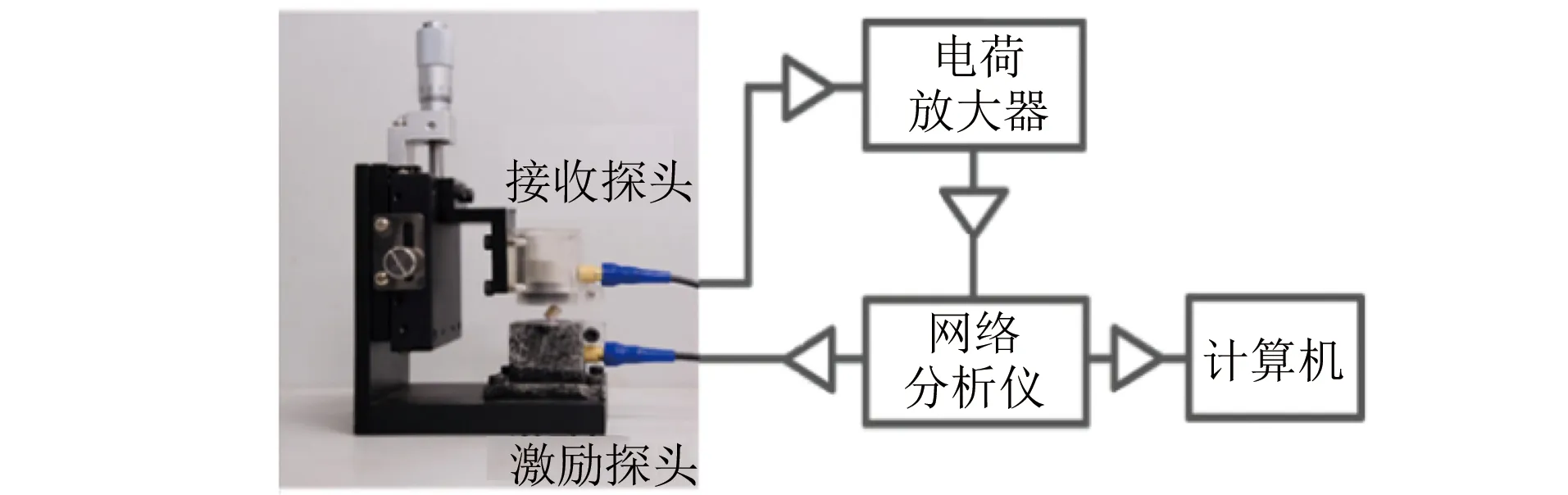
图3 试验系统框图

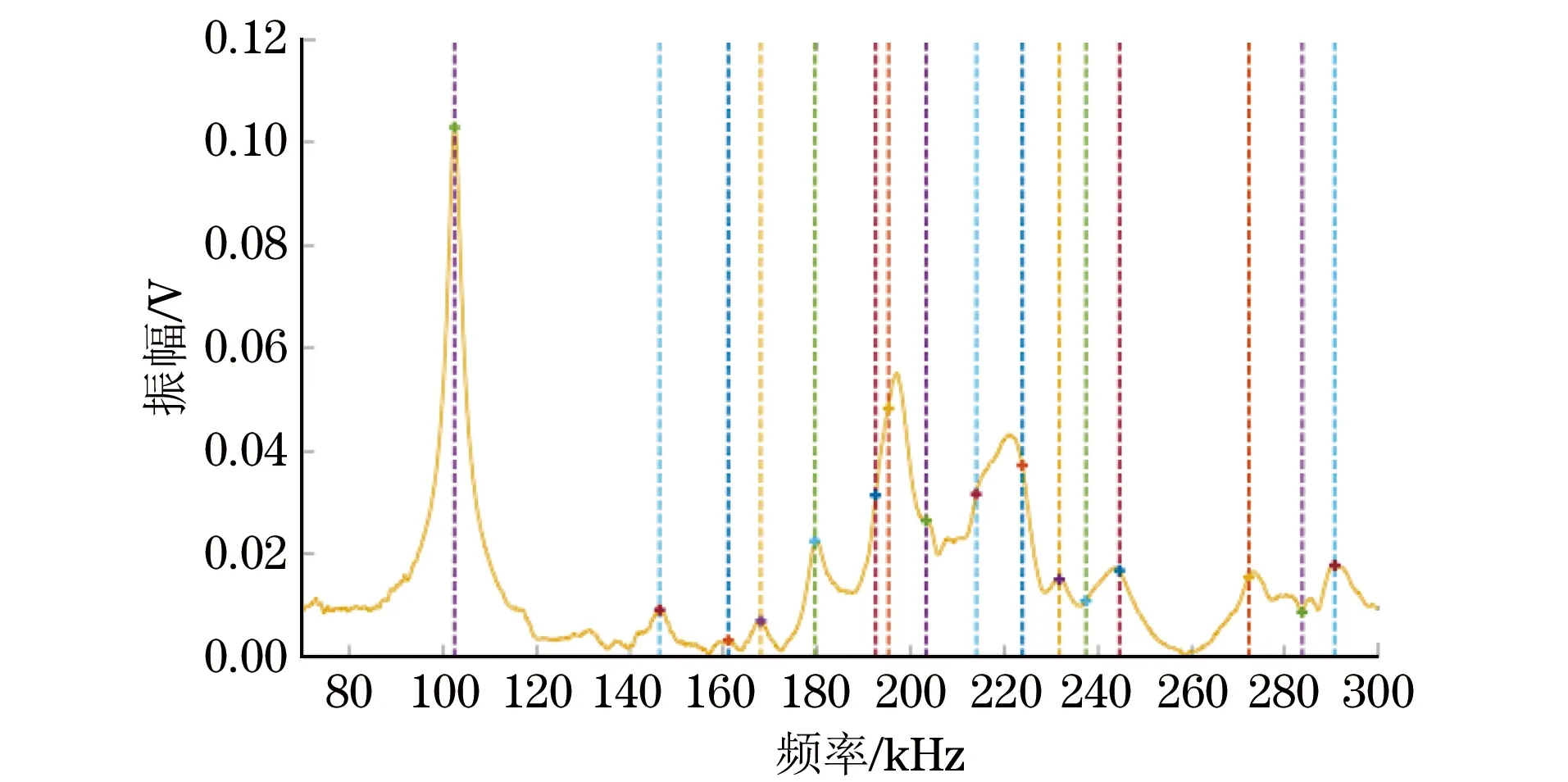
图4 皮质骨模拟材料在70 kHz～300 kHz间的谱线以及提取的16个试验共振频率点

2.2 试验结果

弹性常数的先验来自于前人的皮质骨弹性常数测量结果。

将粒子数设置为50，参数搜索空间设置为先验值的99.7%置信区间，最终优化得到骨模拟材料的弹性常数，并将计算出的杨氏模量与制造商进行拉压试验提供的杨氏模量进行对比，结果见表1。通过弹性常数计算杨氏模量的方法参见文献[10]。结果显示，利用提出的方法计算出的横向杨氏模量Et和纵向杨氏模量Ea与制造商提供的数值具有很好的一致性。

表1 骨模拟材料的弹性常数以及杨氏模量 GPa

同时采用了Levenberg-Marquardt算法进行弹性常数的计算，将初值设置为C11=16 GPa，C33=22 GPa，C12=8 GPa，C13=8 GPa，C44=5 GPa，最终结果与采用粒子群算法计算出的结果相一致。以上两个对比证明了利用粒子群算法可以有效估计出低Q值材料的弹性常数以及工程模量。

需要指出的是，使用LM算法时所设置的弹性常数初值与真实弹性常数非常接近，如果使用皮质骨的统计先验均值作为初值，则无法收敛到该解。这进一步突显出了粒子群算法在初值设置方面的优越性。此外，粒子群算法在计算速度方面表现良好，采用MATLAB软件编程，算法整个优化过程耗时约60 s，远小于基于马尔科夫链蒙特卡洛方法所需要的时间(几十分钟)。

3 结语

RUS作为一种测量材料弹性常数高精度的试验方法，由于模型本身的非凸性以及存在试验共振频率丢失的现象，弹性常数的计算结果严重依赖于初始值设置。针对此问题，提出了基于PSO的优化算法，可有效估计低Q值材料的弹性常数。该算法具有更高的鲁棒性和全局优化能力，在初始值随机设置时表现出了更优的效果，并且相比于马尔科夫链蒙特卡洛方法，计算速度显著提升。此外，算法具有普适性，不但可以估计贝叶斯最大后验概率点，同样适用于最小二乘模型的求解。在未来的工作中，算法有望在效率上进一步提升，如：引入遗传算法的交叉运算，以记录粒子探索过的局部区域；减少计算过程中的无效变异，以节省计算时间。