基于图像处理的膨胀圆裂缝检测算法
吴玉龙,岳大森,丁 勇,卢康昕,赵广辉
(1.昆山市建设工程质量检测中心,昆山 215337;2.南京理工大学 理学院,南 京210094)
裂缝会对房屋结构的防水性、承载力和耐久性产生严重影响,因此对房屋裂缝的检测鉴定是结构检测、危房鉴定和安全监测的重要内容。目前,常采用人工检测手段采集裂缝数据,但该手段具有速度慢、难度大等缺点,因此随着待检测房屋数量的不断增加,传统的人工检测手段已经无法满足庞大的检测任务[1]。
计算机技术在土木工程行业的应用越来越广泛,基于数字图像处理技术的裂缝检测具有非接触式、处理精度高、灵活性高等优点,已成为国内外学者研究的热点。采用数字图像处理技术进行裂缝检测的方法已在裂缝提取方面取得显著成果。然而,此类算法的研究重点一般为图像降噪和阈值分割,对裂缝宽度、长度、面积等参数的图像计算研究较少,难以实现对混凝土表面裂缝的定量分析,不利于数字图像处理技术的现实应用。事实上,在房屋建筑的检测中,裂缝的宽度、长度等参数的测量十分重要[2-3]。
针对上述局限性,笔者提出了一种基于数字图像处理的裂缝参数计算方法,将裂缝假想为被若干圆形充填的平面空间,由一系列可量化的圆的坐标和直径来近似代替,从而实现裂缝几何模型的建立与复原。
1 裂缝宽度
裂缝的产生与发展的理论分析较为复杂,然而,当研究重点放在裂缝参数的计算时,材料构造、结构形式与施工特点将不在考虑的范畴,裂缝问题也随之转化为数学几何形态研究的问题。
裂缝的几何形态为线状,特点为宽度相对较小、长度相对较长、走向斜率变化,具有自然间断和分叉等。现有的裂缝宽度图像常采用法线、平行线等方式计算(见图1),但这些方式存在定义复杂、计算困难的缺点,在多条裂缝的交汇点易产生“伪宽度”,对复杂裂缝的宽度计算时易产生较大误差[4-7]。
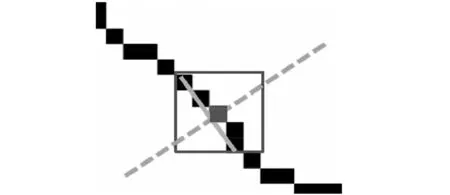
图1 裂缝骨架图像的法线与平行线示意
从另一个角度而言,裂缝可视为若干块刚体(一般为两块)由于相对运动而产生的间隙,该间隙可由某种假想的填充物或图形进行填充。当采用三角形、矩形等多边形进行填充时,存在模型复杂、参数复原缺失等问题,不利于裂缝的参数计算[8-9];而圆形是一种轴对称图形,具有无数条对称轴,其旋转不变性有利于反映裂缝宽度的情况。同时,圆的解析方程是相当成熟而简洁的,因此考虑采用圆作为填充图形,通过圆心、半径、直径等参数反映裂缝参数,进而描述裂缝。假想圆填充裂缝的形状示意如图2所示。
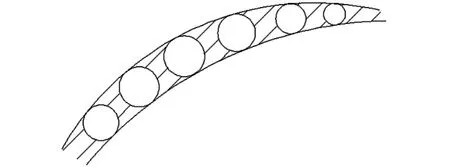
图2 假想圆填充裂缝形状示意
因此,裂缝的宽度可定义为:以裂缝边缘一点为切点的裂缝最大内接圆直径为该处的裂缝宽度。
2 圆的像素级生成
数字图像由像素构成,圆在其中反映为离散的“像素多边形”,因此数字图像中不存在绝对的圆。数字图像中的圆应重新定义,让像素圆的直径在不断增大时,该“像素多边形”越来越平滑,形状和性质也越趋近于圆。
参考圆的定义与标准方程,圆为同一平面内到定点的距离等于定长的点的集合,在平面直角坐标系(xOy)中,以点(a,b)为圆心,r为半径的圆的标准方程为
(x-a)2+(y-b)2=r2
(1)
像素圆是假想填充圆的图形化结果,应视为实心填充圆,同时实心圆也有利于之后的计算。不难得到,像素圆为图像坐标系内到某固定坐标的距离小于等于定长的像素集合。在图像坐标系中,在给定像素圆心坐标(a,b)处生成直径为d的像素圆,考虑到直径像素长度的奇偶差异,对该固定坐标即实际圆心坐标进行规定。
当直径为奇数时,像素圆的实际圆心坐标为(a,b),与像素圆心坐标一致;当直径为偶数时,像素圆的实际圆心坐标为(a+0.5,b+0.5),与像素圆心坐标不同。
下面通过论述像素圆直径的奇偶差异及裂缝宽度的计算原理来说明上述规定的合理性。
数字图像中圆的半径以1像素递增时,直径以2像素递增,故以半径所表示的像素圆将无法连续描述直径,会造成直径缺失奇数,而采用直径表示像素圆时,可以解决该问题。像素圆的像素圆心和实际圆心示意如图3所示。当直径为奇数时,像素圆的圆心为一个像素,实际圆心坐标恰好位于像素圆的圆心上[见图3(a)];当直径为偶数时,单像素的像素圆心无法准确反映实际圆心位置,将该像素沿水平轴线方向和竖直轴线方向分别扩充1像素,形成一个4像素的像素矩形,则实际圆心位于该像素矩形的形心处,等效于将像素坐标沿水平轴线方向和竖直轴线方向分别平移“半个像素”[见图3(b)]。
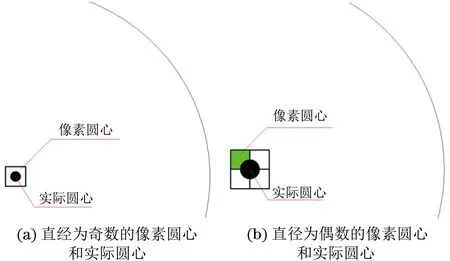
图3 像素圆的像素圆心和实际圆心示意
由此,便得到像素圆心为(a,b),直径为d的像素圆方程,如式(2)所示。
当d=2n-1,n∈N+时
(x-a)2+(y-b)2≤(d/2)2
(2)
当d=2n,n∈N+时
(x-a-0.5)2+(y-b-0.5)2≤(d/2)2
(3)
满足上述方程的像素点集合称为以(a,b)为像素圆心,直径为d的像素圆,采用一行三列的矩阵来表示,记为C=[a,b,d]。图4展示了像素圆直径d由1像素不断增大的图像,可以发现直径在不断增大时,像素圆与实际圆的差异越来越小。
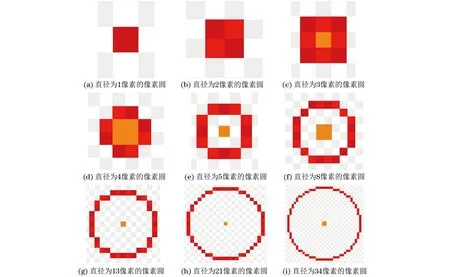
图4 不同直径的像素圆图像
观察不同直径的像素圆图像效果可以发现,直径较小时图像形态与圆存在较大差异,其中从1像素到3像素时的像素圆均为矩形像素,当直径增大至8像素时有了圆形的雏形,直径为34像素的像素圆已十分接近圆形。该算法公式简洁,计算量小,生成效果也较好。在实际检测中,一般侧重于有一定宽度的裂缝,且更为关注裂缝宽度的较大值,因此该像素圆算法作为圆的像素级生成是合理的。
3 膨胀圆算法
由裂缝宽度定义可知,求取某处裂缝宽度的关键在于得到该处的最大内接圆直径。采用一种使像素圆直径由初始值不断增大进而确定宽度像素圆的方法,并将该算法命名为“膨胀圆法”。
裂缝的发展变化会导致最大内接圆同时变化,因而裂缝的发展过程可视为假想填充圆的膨胀过程。由此可知,计算裂缝宽度像素圆可以参考裂缝的扩展过程,通过不断“膨胀”的方式增加其直径,直到满足相切条件,进而动态地求得宽度像素圆矩阵C。
3.1 初始膨胀圆心
若不指定像素圆的初始膨胀圆心,则像素圆的膨胀过程是无序而复杂的,从而极大地耗费计算机资源和计算时间。参考文中所给裂缝宽度的定义,理论上当裂缝恰好被假想圆所填充时,该圆为裂缝的最大内接圆,其圆心应位于裂缝的骨架线也即中轴线上,裂缝骨架线图像如图5所示。因此,不妨将像素圆的初始膨胀圆心定为裂缝骨架线坐标集中的一个,每次膨胀计算时从骨架线坐标矩阵中按一定规则抽取即可。
图5 裂缝骨架线图像
3.2 最大内接像素圆
在数字图像中的相切情况与一般数学意义的相切不同,为保证像素圆的内接,在膨胀至宽度像素圆的过程中,像素圆应始终位于裂缝边缘所构成的封闭区域内。因此,与裂缝一侧相切的交点可能存在多个。图6(b)展示了由图6(a)初始圆心进行膨胀后的结果,该宽度像素圆与裂缝左侧边缘有两个切点,与裂缝右侧边缘仅有一个切点。图7(b)展示了由图7(a)初始圆心进行膨胀后的结果,该宽度像素圆与裂缝左侧边缘有3个切点,与裂缝右侧边缘没有切点,这是因为进一步膨胀会使像素圆超过裂缝区域。
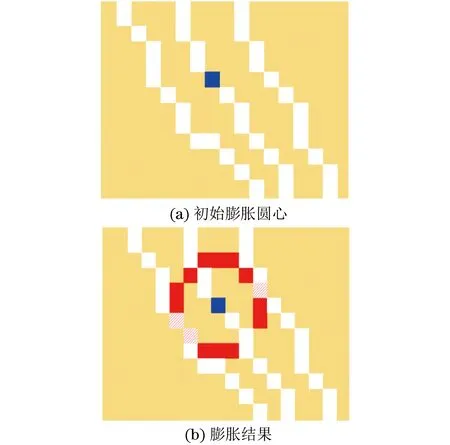
图6 两侧均有切点的宽度像素圆图像
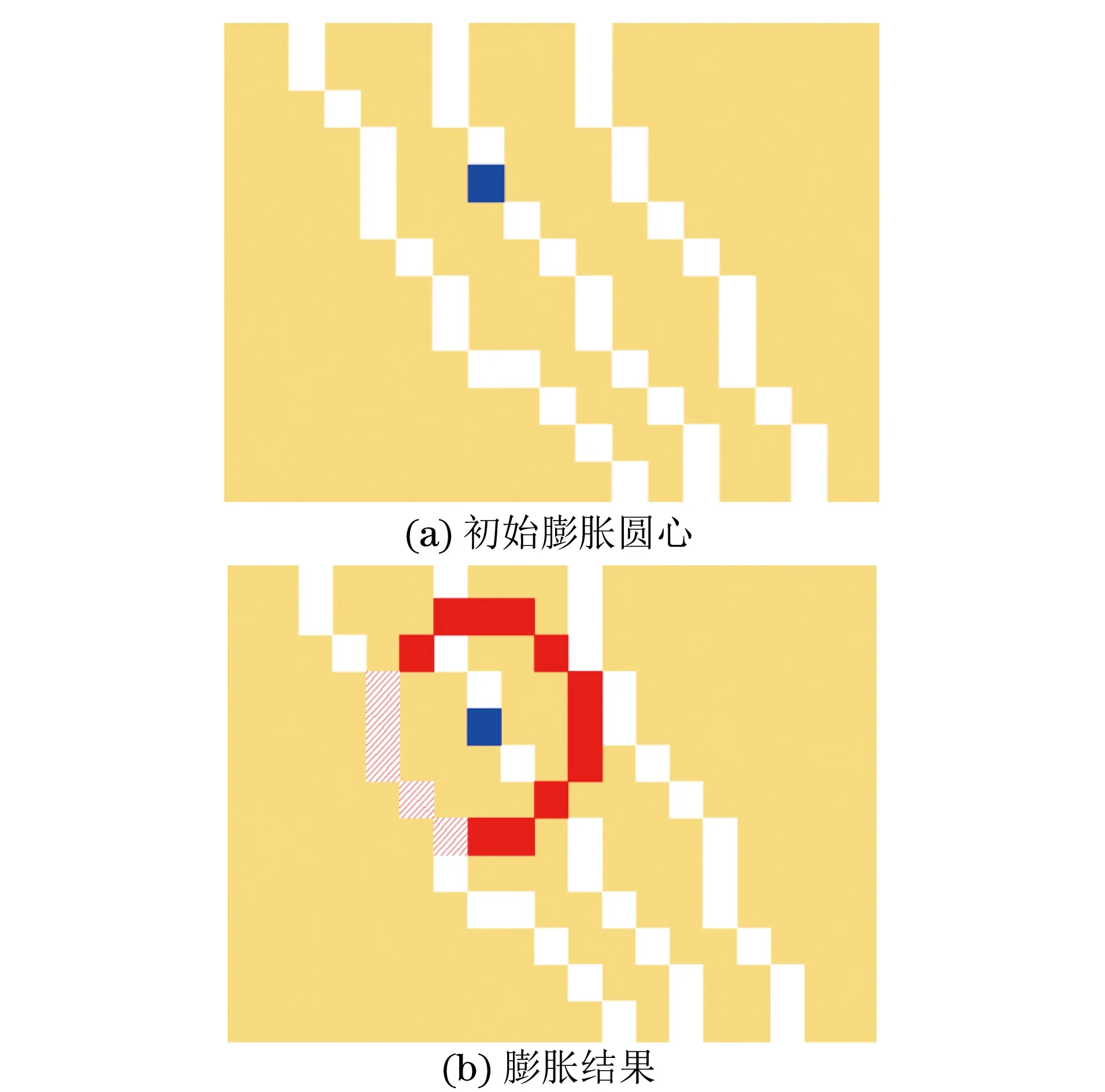
图7 仅一侧有切点的宽度像素圆图像
3.3 膨胀圆疏密度与圆心抽取规则
将裂缝骨架线坐标集合的所有坐标进行膨胀计算并输出的过程繁琐且意义不大,膨胀圆的间距(即疏密程度)会影响计算的效率和准确度。研究的初始膨胀圆心按随机原则从裂缝骨架线坐标矩阵中抽取,在膨胀结束后删除宽度像素圆范围内的骨架线坐标,可以保证相邻宽度像素圆之间不存在空隙,从而实现膨胀圆的疏密度控制。
3.4 膨胀流程
文中重新给出了裂缝宽度的定义,采用一种使像素圆直径由初始值不断增大进而确定宽度像素圆的方法,具体流程如下所述。
(1) 对裂缝二值图像f(x,y)进行骨架提取处理,得到裂缝骨架线及其上各点的坐标,并将坐标值存入骨架线坐标矩阵G中[10]。
(2) 从骨架线坐标矩阵G中随机抽取一组坐标(xi,yi)。
(3) 创建与裂缝二值图f(x,y)相同分辨率的全新图像g(x,y),令新图像中每个像素值均为0,从而使背景为全黑色,随后以步骤(2)中所抽取的坐标为圆心,生成直径为D(初始值D1=1)的白色像素圆[11]。
(4) 将裂缝二值图f(x,y)与生成像素圆的图像g(x,y)进行图像加法运算,得到加和图像m(x,y),并令m(x,y)中大于1的值等于1,使得m(x,y)中仍仅存在0与1[12]。
(5) 将抑制后的加和图m(x,y)与裂缝二值图f(x,y)进行图像减法运算,得到差值图像n(x,y)。
(6) 检索差值图n(x,y)中的像素值,如果n(x,y)矩阵中的元素全为0,则说明步骤(3)中绘制的白色像素圆未接触到裂缝边缘,将直径D增加1,返回步骤(3),重复上述步骤;若第n+1次膨胀后n(x,y)矩阵中元素首次出现1,则说明步骤(3)中绘制的直径为Dn+1的白色实心圆超出裂缝边缘,则结束膨胀,最终膨胀圆直径取Dn=n,记录宽度膨胀圆参数C=(xi,yi,Dn)。
(7) 从骨架线坐标矩阵G中删除该宽度膨胀圆范围内的骨架坐标点,并判断此时矩阵G是否为空矩阵,如果是则结束循环,否则返回步骤(2)并继续循环计算。
4 裂缝图像量化与复原
裂缝图像可经膨胀圆算法进行参数化,使得裂缝由图像转为具有几何意义的宽度膨胀圆参数C,该参数可以用作裂缝的数据进行分析运算,也可以通过连续多张图片所得参数实现裂缝监测、房屋评估等操作。同时,膨胀圆参数可以用来压缩储存空间,将裂缝由图像格式转为数据格式,大大节约了硬盘空间,提高了效率。最后,裂缝图像可由膨胀圆参数进行复原,仍能保留裂缝的主要形态与特征[13-14],膨胀圆法计算得到的裂缝图像如图8所示,裂纹复原与原图重合对比如图9所示。
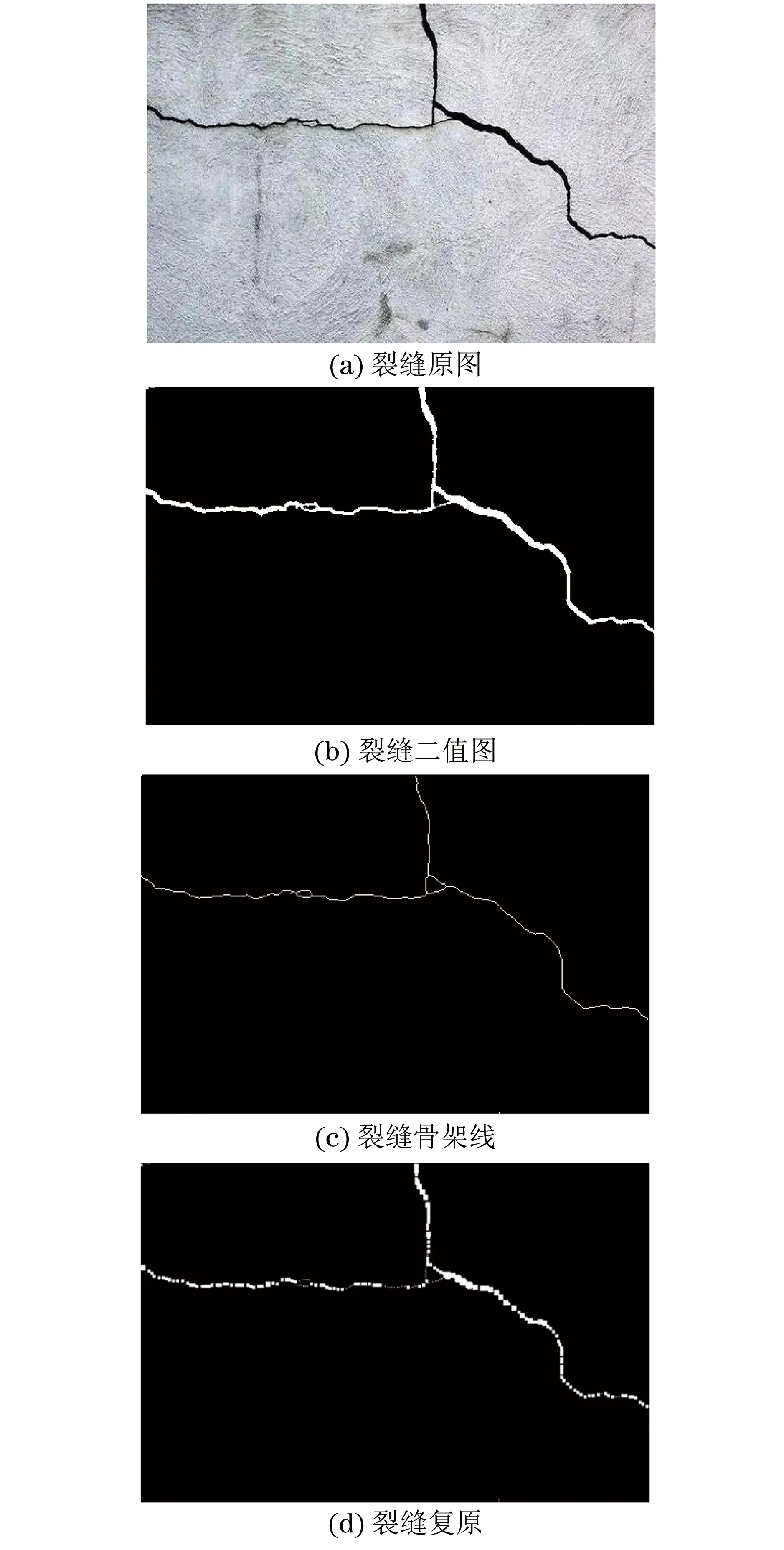
图8 膨胀圆法计算得到的裂缝图像

图9 裂缝复原与原图重合对比
5 结语
提出了一套基于数字图像处理的裂缝参数计算方法,能够从裂缝二值图像中提取参数,并将裂缝信息由图像格式转换为数据格式,该方法的优势如下所述。
(1) 裂缝宽度计算适用性强,应用范围广,可有效计算复杂裂缝与交错裂缝的宽度。
(2) 由于算法与裂缝宽度的定义相吻合,得到宽度的同时能够给出宽度坐标,因而其宽度计算与定位结果较为准确,宽度情况反映较为全面。
(3) 裂缝参数化后由图像格式转为数据格式,节约了存储空间,有利于裂缝的长期监测,必要时可由宽度膨胀圆参数进行复原,仍保留了裂缝的主要形态与特征。
(4) 裂缝的膨胀圆参数是裂缝的几何及数学信息,可用于裂缝或者结构健康评估的进一步分析运算。

