工字型钢框架极限承载力分析的通用广义屈服函数

杨绿峰，谭夏墉，韩晶晶

(1.广西大学土木建筑工程学院，广西，南宁530004；2. 广西大学工程防灾与结构安全教育部重点实验室，广西，南宁530004)

工字型和H 型钢截面具有抗弯能力强、用料省的特点，欧美等国家规范[1−2]中通常将二者合并表达为工字型钢，在各种工业和民用建筑结构、尤其是大跨度工业厂房和高层建筑的框架结构中得到广泛应用[3−4]，其极限承载力是保证结构安全使用的关键。广义屈服函数(Generalized Yield Function，简记为GYF)[5]是表征构件发生全截面屈服时不同内力分量与截面强度之间必须满足的函数关系式，与截面几何形状和材料特性密切相关，是开展构件极限承载力分析和设计的基础。

国内外针对工字型截面的GYF开展了广泛研究，但是，由于工字型截面的力学性能与腹板、翼缘的尺寸相关，几何特征参数多，其广义屈服函数难以精确地显式表达。Chen 和Atsuta[6]通过叠加法建立了工字型截面在轴力及双向弯矩作用下GYF的相对精确解，但需要通过方程组隐式表达，难以在工程实践中应用。胡淑军等[7]利用截面组合法建立了简化的平面内受力工字型截面GYF的隐式方程组。Chen 和Atsuta[6]、Orbison 等[8]研究建立了空间受力下工字型截面GYF的显性近似表达式，便于工程应用，但没有考虑截面几何尺寸的影响。Duan 和Chen[9]、Gendy 和Saleeb[10]进一步以腹板与单翼缘面积之比 γ1作为几何参数，通过拟合分析研究建立了空间受力下工字型截面GYF的显性表达式，得到了较为广泛的应用[11−13]。但是，由于工字型截面的几何特性相对复杂，仅用 γ1难以准确表征，导致文献[9− 10]建立的GYF存在计算精度差和通用性不足的问题。

同时，弹性模量调整法[14]是一类原理简明且精度较高的线弹性迭代分析方法，在结构极限承载力分析中得到广泛应用。为了提升弹性模量调整法在大型建筑结构中的效率，Marin-Artieda和Dargush[5]、Hamilton 和Boyle[15]、杨绿峰等[16]引入GYF，并利用板壳单元或梁柱单元建立结构有限元模型，大大降低了离散自由度。但是传统工字型钢的GYF均为非齐次函数，不满足塑性极限分析的比例条件[17−18]，导致弹性模量调整法的计算结果会受到初始荷载取值影响，计算结果不稳定、精度不足。为此，杨绿峰等[18]通过建立齐次广义屈服函数(Homogenous GYF，简记为HGYF)提出了能高效、稳定求解结构极限承载力的弹性模量缩减法(Elastic Modulus Reduction Method，简记为EMRM)，具有很高的计算精度和效率。张伟等[19]在此基础上建立了工字型钢的HGYF，但没有全面考虑截面几何参数的影响，导致其计算精度和通用性不佳。

本文在对比分析截面几何参数对工字型截面GYF计算精度和适用性影响的基础上，通过回归分析建立了具有较强适用性和较高拟合精度的工字型截面通用HGYF，进而结合弹性模量缩减策略，建立了工字型截面框架结构极限承载力分析的高效高精度线弹性迭代方法。

1 传统工字型截面的广义屈服函数

1.1 隐性广义屈服函数

GYF与截面受力状态、几何参数和材料屈服准则等因素有关，其中，材料屈服准则多采用Von-Mises准则[20−21]。截面受力状态和几何参数是目前建立构件截面GYF的主要考虑因素。

对于图1(a)所示的工字型构件，截面受轴力Nx、双向弯矩My和Mz作用，截面几何参数如图1(b)所示，其中h、b、tf和tw分别为截面高度、宽度、翼缘厚度和腹板厚度。Santathadaporn 和Chen[6]根据极限分析的界限定理建立了工字型截面广义屈服函数的隐性表达式，且表现为上下限函数。进一步地，Chen 和Atsuta[6]通过叠加边长分别为(b,h)、(b,h−2tf)和(tw,h−2tf)的三个矩形截面上的内力，建立工字型截面的内力Nx、My和Mz的计算表达式如下：

根据式(1)确定的内力关系可以判别工字型截面在任意一组内力(Nx,My,Mz)作用下是否进入塑性极限状态，是GYF的隐式函数，尽管该函数能够精确表达工字型截面的GYF，但不便于应用。

1.2 显性广义屈服函数

胡淑军等[7]基于截面组合法建立了轴力Nx和强轴向弯矩My共同作用的精确GYF的隐性方程组，适合于平面内受力结构。为了便于使用，本文通过进一步分析和推导，建立了该GYF的显性表达式：

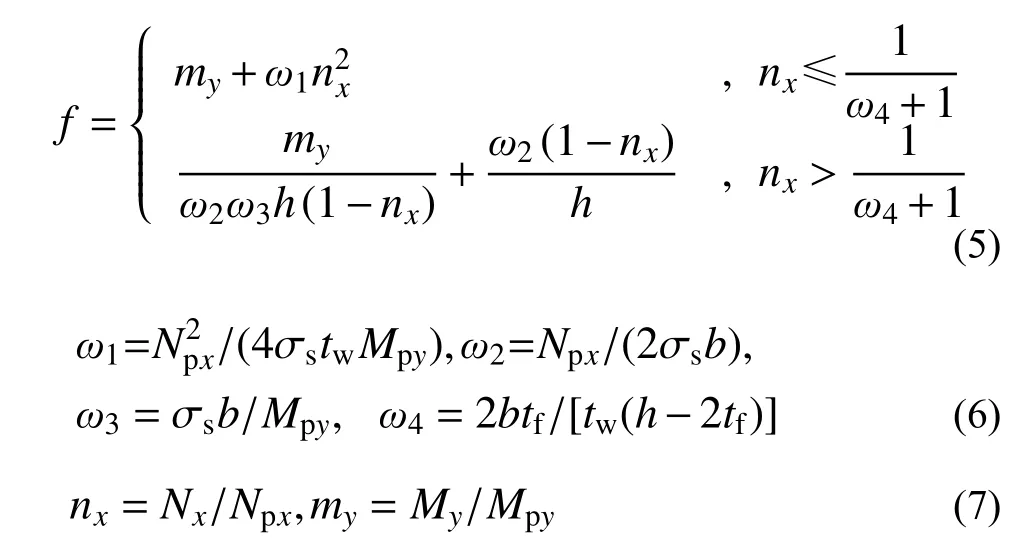
式中：nx和my分别为对应于Nx和My的无量纲内力；Npx和Mpy分别为轴向强度和抗弯强度，也称为全截面塑性内力；ω1～ω4为与截面尺寸有关的参数。

考虑到实际应用中有必要考虑空间受力问题，Chen 和Atsuta[6]进一步提出了空间受力的工字型截面GYF的近似表达式：

GYF与构件截面几何特性和材料特性密切相关，而式(8)、式(10)都没有考虑工字型截面几何参数的影响，因而影响两者的计算精度。

为此，Duan 和Chen[9]建立了具有双轴对称(包括箱型、工字型等)截面的GYF：

1.3 截面几何参数对广义屈服函数的影响

式(12)和式(15)中的几何参数γ1只考虑了腹板和单翼缘面积比的影响，难以全面反映工字型截面的几何特性。为此，这里增加考虑几何参数γ2：

由于h/tf=γ1γ2+2，因而参数γ1、γ2可以间接表征几何参数h和tf，因而能够全面表达工字型截面的几何特征。这里以式(1)中的GYF为基准对比分析其他GYF的拟合精度和适用性。表1给出了三个工字型截面的几何参数。

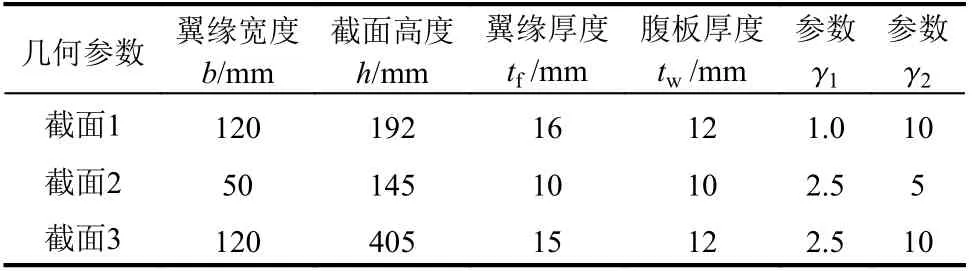
表1 工字型截面尺寸Table 1 Sectional dimensions of I-sections

首先，根据式(1)绘制三个截面的精确GYF，如图2所示。从图2中可以看出，尽管截面1和截面3具有相同的γ2取值，但当γ1发生变化时，两者的GYF随之发生改变；同时截面2和截面3具有相同的γ1，但当γ2发生变化时，两者的GYF也随之发生改变。由此说明工字型钢截面的GYF与几何参数γ1和γ2有较密切的关系。

进一步地，根据式(8)、式(10)、式(11)、式(13)和式(14)绘制不同的工字型截面显性近似GYF关于表1中截面1和截面2的曲线，并与式(1)精确GYF相比较，如图3所示。从图3(a)可见，除式(14)的线性GYF误差较大外，其余近似GYF精度较高，说明传统的近似GYF对于部分截面尺寸有一定的适用性。

进而，从图3(b)可见，5个显式GYF都与隐式精确GYF有较大的差距，其中式(14)的线性GYF误差最大，其次是式(8)和式(10)的近似GYF。而式(11)和式(13)的近似GYF尽管拟合精度有所改进，但与精确GYF之间仍有显著误差。主要原因在于，式(14)的GYF为线性函数，难以合理拟合非线性GYF；式(8)、式(10)的GYF都没有考虑截面几何参数γ1和γ2的影响；式(11)、式(13)和式(14)考虑了参数γ1，但未考虑参数γ2的影响。由此说明在建立工字型钢的GYF时有必要全面考虑截面几何参数γ1和γ2的影响。

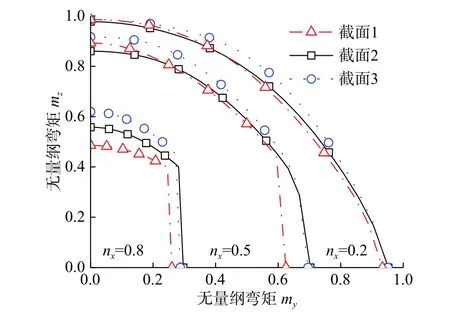
图2 精确GYF曲线Fig.2 Exact GYFcurves

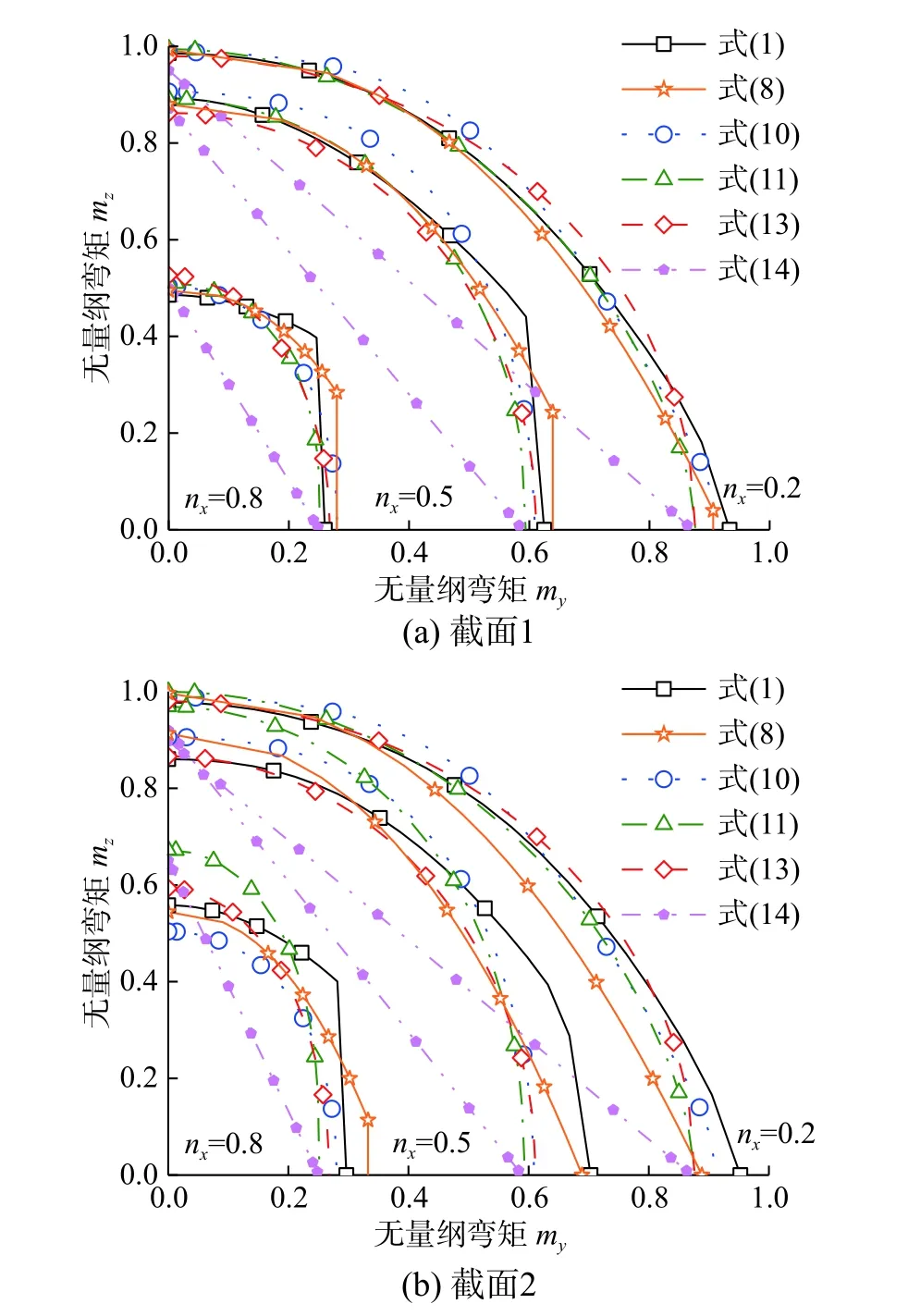
图3 传统GYF曲线Fig.3 Traditional GYFcurves

2 齐次广义屈服函数

2.1 逐步回归分析与齐次函数

从1.1节可以看出，式(1)建立的工字型截面精确GYF为隐性函数表达式，不便于使用。而现有的显性近似GYF在精度和适用性方面都存在不足，并且上述GYF用于结构极限承载力分析时都不满足比例条件。文献[19]建立的工字型截面HGYF尽管能够满足比例条件，但继承了式(11)的不足，没有考虑几何参数γ2的影响，导致计算精度和适用性都有局限性。为此，这里同时考虑几何参数γ1和γ2的影响，研究建立工字型截面高精度通用HGYF，具体步骤如下：

2.1.1建立HGYF表达式

2.1.2确定拟合分析的样本点

根据我国常用工字型截面型钢表[23]以及美国材料与试验协会标准ASTM-A6/A6M 中的型钢截面规格确定γ1和γ2的常见取值范围γ1∈(0.3,3)，γ2∈(5,50)，并分别按照步长0.3和5均匀配置γ1和γ2在各自取值范围内的取值点，由此确定100组常见工字型截面的几何特征参数(γ1j,γ2j)，j=1, 2,···,100。然后根据式(1)中的精确GYF，计算每个工字型截面上满足广义屈服条件的无量纲内力，每一组内力形成一个样本点( γ1i,γ2i,nix,miy,m iz)。通过在屈服面上均匀取值可以确定42 100组屈服面样本点。

2.1.3根据拟合误差分析确定

根据上述确定的所有样本点，通过线性回归分析确定式(17)和式(18)中的待定系数，使得残差平方和Π 最小，即：

通过回归分析可以得到不同阶次s时的拟合均方根误差和可决系数，如表2所示。

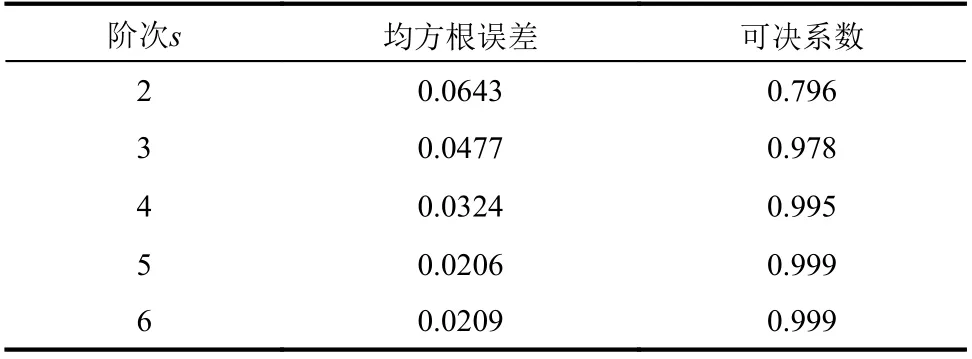
表2 不同阶次HGYF的拟合精度Table 2 Fitting accuracy of HGYFswith different orders

由表2可见，s对均方根误差和可决系数有着显著影响，均方根误差随着s增大而逐渐减小，可决系数随着s增大而逐渐增大。当s>4时，均方根误差不超过0.03，同时可决系数稳定在0.99以上，充分说明了齐次函数具有较高的拟合精度。

2.1.4简化HGYF表达式

2.1.1 节～2.1.3节中建立的HGYF表达式是包含了所有齐次项的完整表达式，且随着阶次增加，齐次函数的项数也快速增加，表达式较为复杂。为此，可通过逐步回归分析对变量进行筛选，逐步引入显著性大(影响大)的变量，剔除不显著(影响小)的变量，由此得到简化的HGYF表达式。这里基于均方根误差的容许值以及可决系数选取回归模型，建立HGYF简化表达式。当s取值2～6时，通过逐步回归分析确定的HGYF的可决系数如表3所示。由表3可见，在相同均方根误差容许值下，阶次越大，可决系数越大。

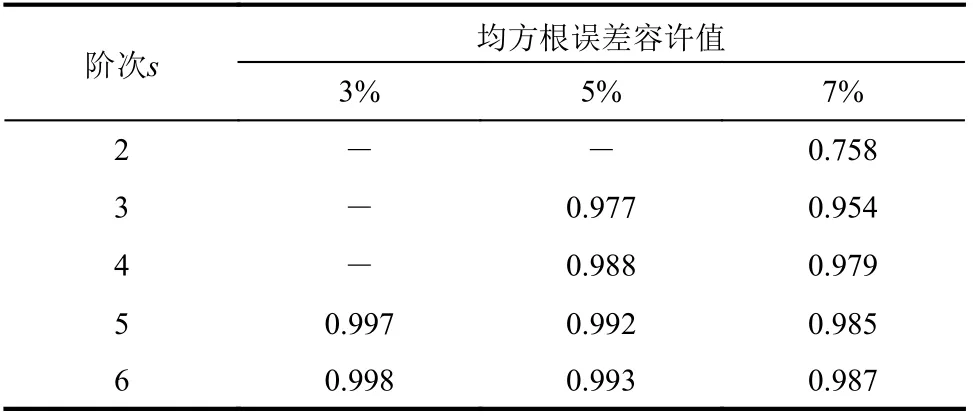
表3 不同回归模型的最大可决系数Table 3 Maximum R2 of different regression models

进一步以表1中截面1为例，当均方根误差容许值取7%时，不同阶次s的HGYF与式(1)精确GYF的对比如图4所示。从图4中可以看出2阶HGYF曲面与精确GYF曲面在my=0附近处有明显的分离现象。随着HGYF阶次的增大，与精确GYF的吻合程度逐步提高，且4阶HGYF与精确GYF能够较好吻合。

综合考虑表3和图4中不同阶次HGYF的拟合精度，均方根误差容许值取5%时的3阶、4阶HGYF的可决系数分别达到0.977和0.988，且与精确GYF基本吻合。本文取4阶HGYF，具体表达式为：

2.2 齐次广义屈服函数的精度与通用性

以式(1)中的隐式精确GYF为基准，结合表1中的3个截面对比分析本文的HGYF和文献[19]的HGYF的精度和适用性，如图5所示。从图5中可见，本文HGYF始终与精确GYF吻合较好。同时，文献[19]的HGYF只对截面1取得较好的拟合精度，而对截面2和截面3的拟合效果较差，这与图3中式(11)的GYF具有相同的表现，两者都对截面1拟合较好而对截面2拟合效果较差。其原因在于本文HGYF同时考虑了γ1和γ2两个截面几何参数的影响，具有较高的计算精度和广泛适用性，而文献[19]的HGYF是基于对式(11)的GYF拟合分析而建立的，因此继承了该GYF仅考虑几何参数γ1，而忽略γ2影响的缺陷，导致其适应性和计算精度较差。

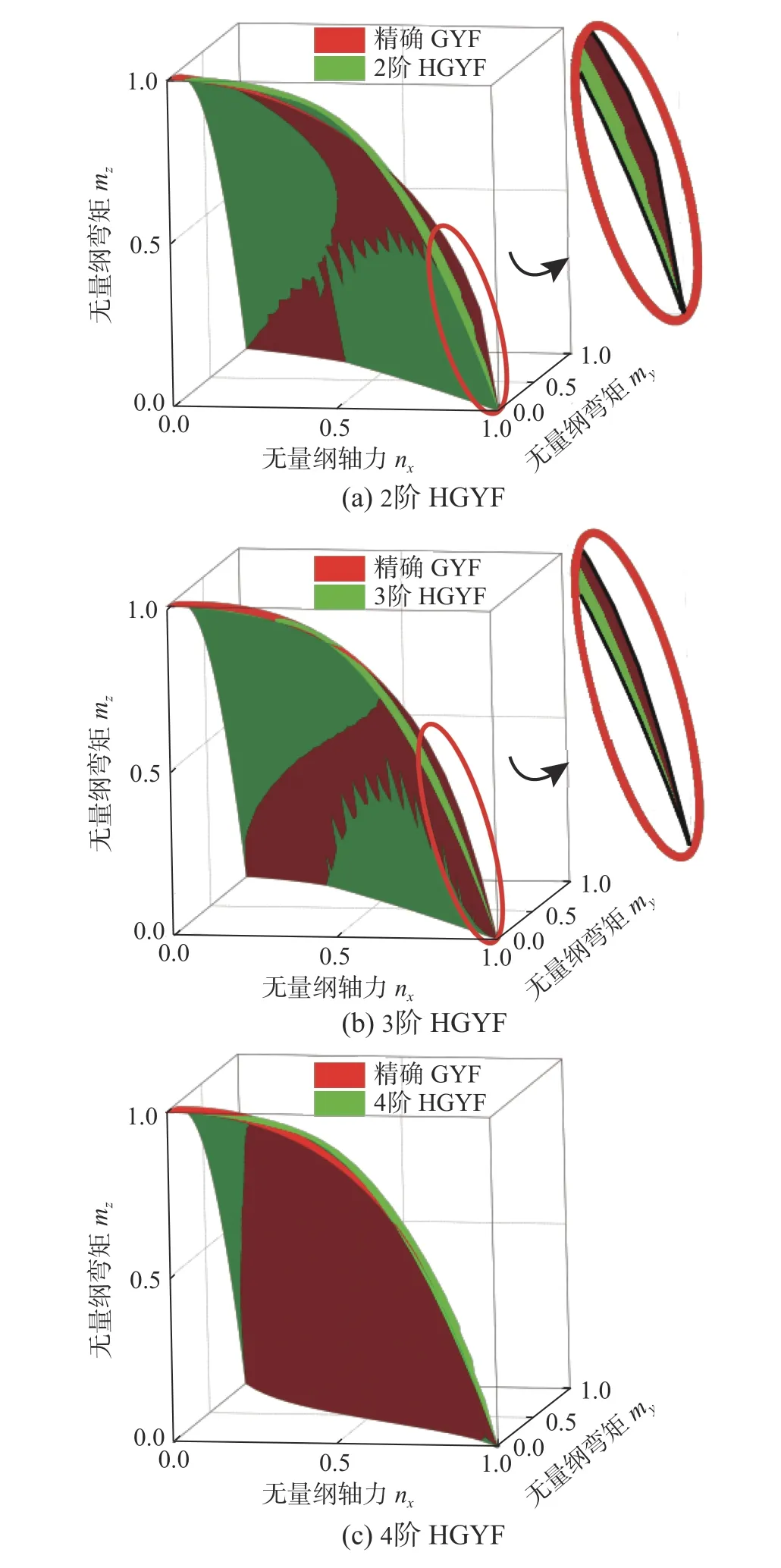
图4 精确GYF与不同阶次HGYF对比Fig.4 Comparison between exact GYFand HGYFs with different orders

3 极限承载力分析的线弹性迭代方法

根据框架结构的线弹性内力和式(24)建立的齐次广义屈服函数，可定义单元承载比：

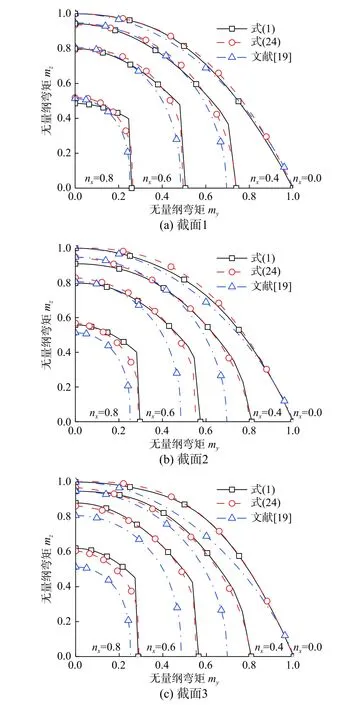
图5 精确GYF和HGYF对比Fig.5 Comparison between exact GYFand HGYF

4 算例分析

本文采用商业软件ANSYS建立有限元模型，并利用EMRM求解平面以及空间荷载下的工字型截面钢框架结构极限承载力。对比分析不同GYF和HGYF对EMRM 计算结果的影响，进一步地通过与基于塑性极限分析理论的解析解和弹塑性增量分析法(EPIA)[24−25]计算结果进行对比分析，论证EMRM的计算精度和效率。有限元模型中，离散单元类型选用beam189，框架材料的弹性模量E=2.0×105MPa，屈服强度为σs=200 MPa。EPIA采用理想弹塑性本构模型和力的2-范数收敛准则。台式PC机配置CPU@3.60 GHz，内存16.0 G。

4.1 单层单跨平面框架

图6 单层单跨框架Fig.6 Single-story and single-span frame

图6所示的单层单跨工字型截面平面框架，跨度L和层高H均为3 m，构件为美国型钢W14×426。框架左侧柱顶作用有水平集中荷载P。基于塑性极限分析理论[26]求得该框架的塑性极限荷载解析解为1881.10 kN。进一步地，分别利用EMRM和EPIA 计算该框架的极限承载力，并以解析解为基准对比分析EMRM 和EPIA 计算结果的精度、效率和适应性。

4.1.1有限元离散方案

为了分析有限元法不同离散方案对精度的影响，分别利用EMRM和EPIA 计算不同离散方案时的框架极限承载力，计算结果与解析解之间的误差以及CPU 计算耗时见表4。

表4 收敛性分析Table 4 Analysisof convergence

从表4中可以看出，对于EPIA，当每个构件离散为6个单元时计算结果收敛。而对于EMRM，当每个构件离散为2个单元时，计算结果已收敛。此时，EMRM和EPIA 计算结果与解析解之间的相对误差er分别为0.5%和5.8%，且EMRM的计算耗时尚不到EPIA 的一半，由此说明，EMRM具有较高的计算精度和计算效率。

4.1.2不同GYF的对比分析

为了比较分析传统GYF和本文HGYF对EMRM结果的不同影响，这里分别将式(8)、式(11)的GYF和本文的HGYF代入式(26)定义不同的单元承载比，在此基础上进行EMRM计算分析，确定框架结构的极限承载力。分别取荷载P0的初值为10 kN和100 kN 并进行极限承载力分析，此时EMRM的迭代求解过程如图7所示，相应的计算结果见表5。从图7中可以看出，采用式(8)和式(11)的GYF定义单元承载比时，EMRM的迭代分析过程波动大，收敛速度慢，且计算结果随荷载初值P0的改变而改变。这是因为传统GYF多为非齐次函数，单元承载比与内力变化不成比例，因此计算不稳定，导致计算精度难以满足要求。同时也可以看到，利用式(24)中HGYF定义单元承载比，可以使得EMRM计算结果不再受初始荷载影响，且仅需很少的迭代步即可得到高精度的收敛结果。

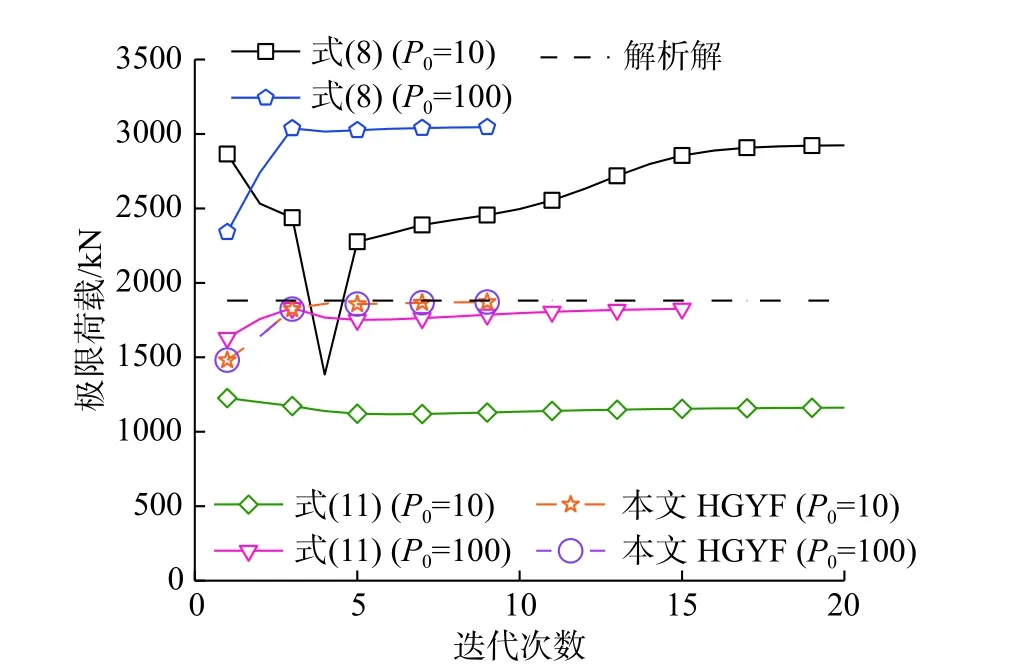
图7 极限荷载迭代过程Fig.7 Iterative process for ultimate load

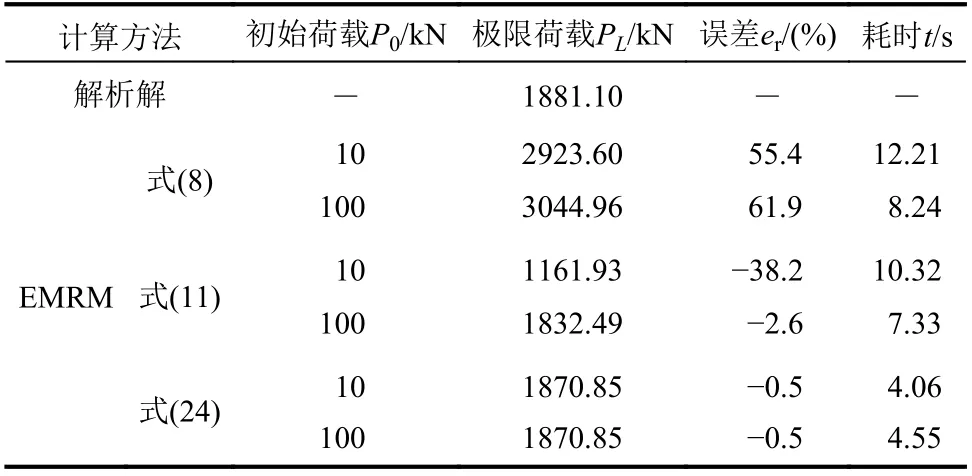
表5 荷载初值对结构极限承载力的影响Table5 Influenceof initial load on ultimate strength of structure

4.1.3适用性分析

为讨论本文HGYF对不同工字型截面的适用性，依次选取热轧普通工字钢I18和I63c、热轧轻型工字钢I70以及美国型钢W36×232作为本算例框架中的梁柱构件，具体截面尺寸见表6，分别利用EMRM和EPIA 分析刚架的极限承载力，并将计算结果同解析解对比，详见表7。

表6 工字型截面尺寸Table 6 Sectional dimensions of I-sections

从表7可以看出，相较于EPIA，采用基于本文HGYF的EMRM 进行结构极限承载力分析能够取得更高的计算精度，与解析解之间的相对误差不超过0.4%，且计算时间不及EPIA 的一半。而且结合表6和表7可以看出，对于具有不同γ1、γ2的型钢构件，本文方法始终保持较高的计算精度和效率，再次证明本文方法具有良好的适应性。

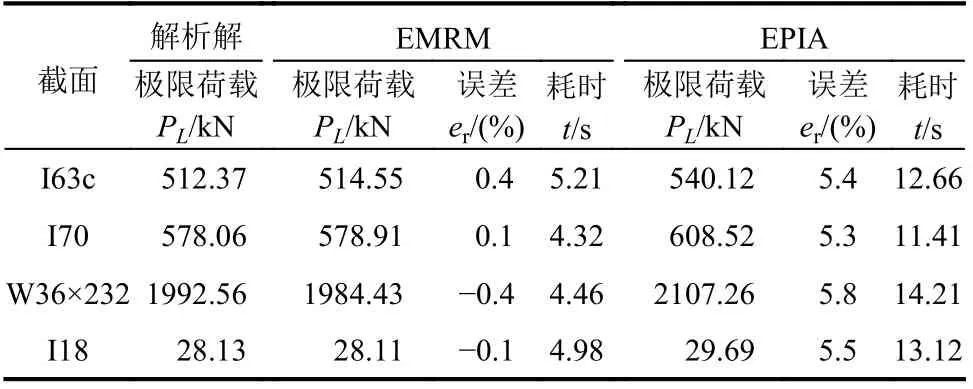
表7 γ1和γ2 对计算结果的影响Table 7 Influence of γ1 and γ2 on results

4.2 多层多跨空间框架

图8所示采用工字型构件的多层多跨空间框架，底端固定，跨度L=4.8 m，层高H=3 m，构件为美国型钢W14×426。框架梁顶面受竖直向下的均布荷载q作用，左侧框架柱顶端受水平向右的集中荷载qL作用，可用向量P=(q,P)=P0(1.0,L)表示两个荷载作用，其中P0=q称为荷载乘子，常用来代表荷载P开展结构极限承载力分析。

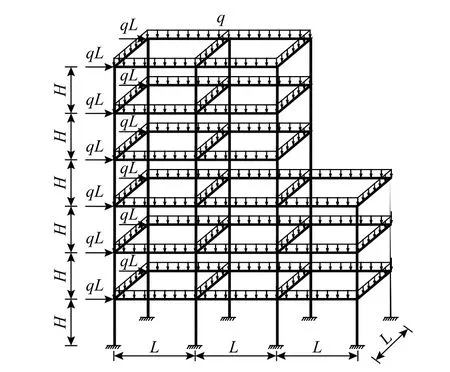
图8 多层多跨空间刚架Fig.8 Multi-story and multi-span space frame

4.2.1有限元离散方案

为了分析有限元法不同离散方案对空间钢框架极限承载力计算精度的影响，分别利用EMRM和EPIA 计算不同离散方案下的极限承载力，结果如表8所示。从表8中可以看出，对于EPIA，当每个构件离散为4～6个单元时结果收敛。而对于EMRM，当每个构件离散为2个单元时结果已经收敛。考虑到EPIA 计算结果将用于检验EMRM计算精度的基准，这里选取构件离散单元数为6。此时，EMRM计算得到的极限承载力与EPIA 结果的相对差er在6%左右，而CPU 计算耗时t远远低于EPIA，说明EMRM具有较高的计算精度和计算效率。

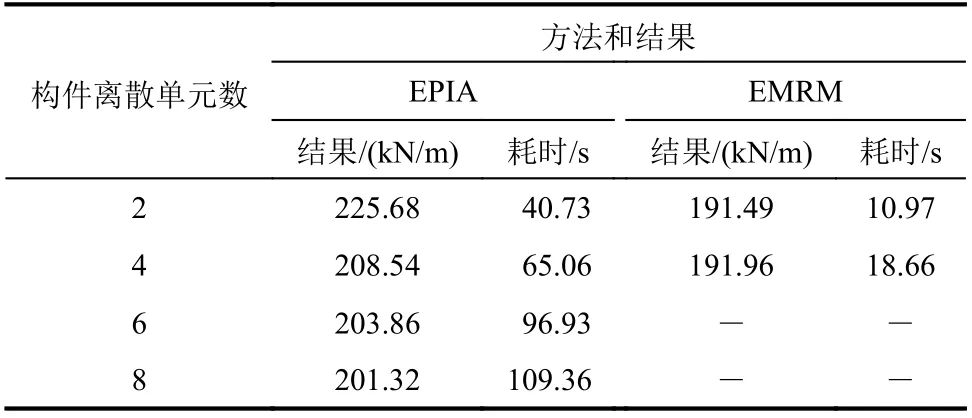
表8 收敛性分析Table 8 Analysisof convergence

4.2.2荷载初值影响分析

为了比较分析空间框架结构中传统GYF和本文HGYF对EMRM结果的不同影响，分别将式(8)、式(11)的GYF和本文的HGYF代入式(26)定义不同的单元承载比，在此基础上利用EMRM计算分析空间框架结构的极限承载力。当分别选取荷载P0的初值为10 kN/m 和100 kN/m 时EMRM的迭代求解过程如图9所示，相应的计算结果见表9。从图9 中可以看出，空间框架与平面框架结构的计算结果类似，采用式(8)和式(11)的GYF定义单元承载比时，EMRM的迭代分析过程及计算结果随荷载初值P0的改变而改变，而利用本文HGYF定义单元承载比，EMRM计算结果不再受初始荷载影响。

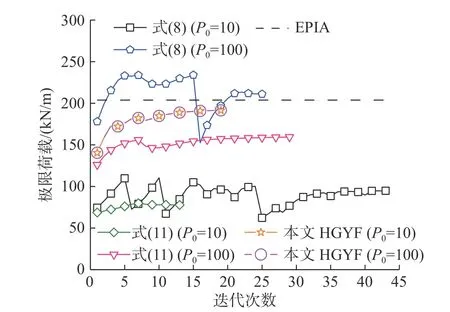
图9 极限荷载迭代过程Fig.9 Iterative process of ultimate load

4.2.3适用性分析

利用基于本文HGYF的EMRM 和EPIA 分析空间框架结构的极限承载力，构件的截面尺寸如表6所示，计算结果见表10。

由表10可知，相较于EPIA，采用基于本文HGYF的EMRM计算复杂空间框架结构的极限承载力时仍然能够取得较高的计算精度，两者之间的相对误差最高在6%左右，且EMRM 有更高的计算效率，计算耗时远远低于EPIA。充分证明了本文HGYF和EMRM 具有较强的适用性。

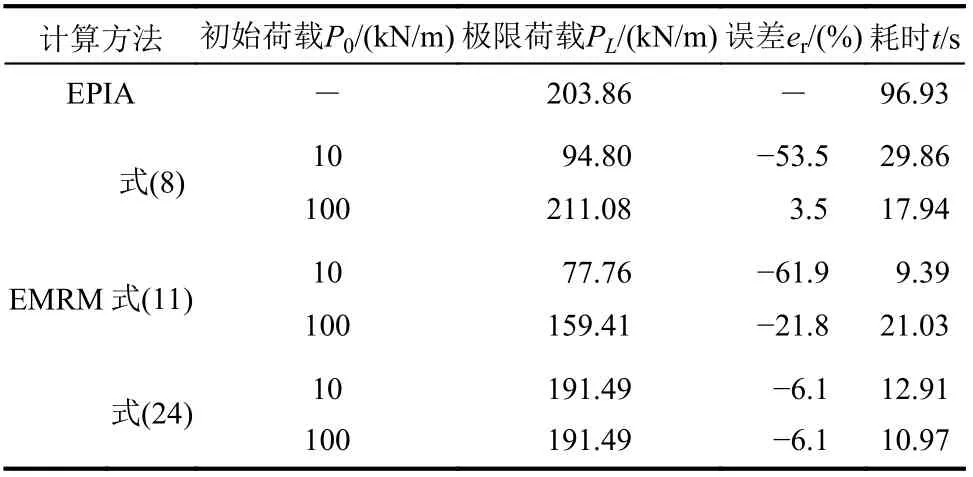
表9 荷载初值对结构极限承载力的影响Table 9 Influence of initial load on ultimate strength of structure

表10 截面几何参数γ1和γ2对计算结果的影响Table 10 Influence of γ1 and γ2 on results

5 结论

本文通过逐步回归分析建立了工字型截面的通用齐次广义屈服函数，提出了平面及空间受力下工字型截面框架结构极限承载力分析的高效高精度线弹性迭代方法，并得到如下结论：

(1)本文建立的工字型截面齐次广义屈服函数利用两个比例参数γ1和γ2全面考虑截面几何特征的影响，适用于平面及空间框架结构，具有较好的通用性，且计算精度高，克服了现有工字型截面广义屈服函数通用性差、计算精度不足的问题。

(2)基于齐次广义屈服函数建立的工字型截面框架结构极限承载力分析的线弹性迭代方法计算结果不受初始荷载影响，迭代过程稳定，克服了传统方法容易受荷载初始值影响、迭代计算过程不稳定的缺陷，具有较高的计算精度和计算效率。