场地校正的地表PGA 放大系数概率模型研究

唐 川，陈龙伟

(中国地震局工程力学研究所，中国地震局地震工程与工程振动重点实验室，哈尔滨150080)

地表峰值加速度PGA 是抗震设计规范中一个重要指标参数，其在地震预警与地震烈度速报技术中扮演着重要角色[1−4]，同时也是工程结构抗震设计中地震作用特性的直观表征参数[5]。PGA 参数的获取一是通过强震台站的记录，而对于没有台站以及地震活动性弱的地区，则采用地震动预测方程(ground motion prediction equation, GMPE)进行预测[6−8]，或者通过震后震害调查得到的烈度转化[9]。采用GMPE 预测地震动参数，本质上是给出具有共性的某一“类”场地的地震动参数预测，在针对具体场地时，需要根据场地特征进行必要的修正[10−11]。场地条件对地震动的影响显著已经是不争的事实，所以在现行的国内外常用的GMPE 中多加入了场地特征参数(如Vs30、Z1.0等)的影响[8,12]。历次震害资料表明，场地近地表土层介质对地震波传播影响较大，主要表现为对不同频率的地震波成分的放大和滤波作用，所以即使震源距相同的区域，地表地震动也会存在一定的差异性，直接影响到地震灾害的分布[13]。所以，工程结构的抗震设计及试验的数值模拟中，考虑场地条件的地震动场估计是其必要环节[14−15]。目前国内地震预警系统中采用的GMPE多未考虑场地条件的影响，而随着地震预警和烈度速报技术的优化，亟需解决PGA 估计的场地条件校正问题。

场地PGA 放大系数fPGA是反映场地土层对地震动峰值作用的指标，已有国内外学者研究放大系数与场地特征参数之间的关联性。Yoshikazu 等[16]通过土层与基岩的剪切波阻抗比以及Vs30和Vs10估算场地PGA 放大系数，发现Vs10与PGA的相关性较好，而Vs30与PGV 的相关性比PGA 的相关性要强。Hamidreza 通过人工神经网络的方法比较不同的土层特性对PGA 放大系数的影响，发现剪切波速和土层厚度能更有效的决定PGA 放大系数[17]。Nilsun 提出了以Vs-SPT 的经验关系估算场地放大函数的经验方法，但与数值模拟以及微震方法获取的放大系数相比，其得到的放大系数偏小[18]。任叶飞等[19]在结构抗倒塌易损性分析中采用震级、距离和Vs30作为变量控制对工程输入地震动进行分组。Regnier 等[20]通过KiK-net 数据库提出采用Vs30、场地卓越周期以及剪切波速沿深度梯度的组合能更合理地评估场地放大效应。从以往研究结果来看，场地土层剪切波速和土层厚度是场地地震响应密切相关的特征参数，而这两个参数在工程勘察亦容易获取，所以，建立fPGA与这两特征参数之间的关系，可实现对场地校正的PGA 值进行快速估计[21]。随着风险评估等概念在工程上的实施，PGA 预测亦应含概率意义，这方面的研究国内尚不多见，主要局限于强震数据的不足。国内外的强震数据库中，日本的KiK-net[22]不仅提供高质量的地表和井下强震记录，而且给出台站场地土层信息，为地震工程研究提供良好平台，本文研究亦基于此数据库。

本文选取KiK-net 台网的40个台站，收集整理自1996年3月至2019年5月台站记录的地震加速度数据，包括地表和井下加速度时程记录。分析实测PGA 放大系数fPGA及其概率分布特征，确定其概率密度函数；分析单台PGA 放大系数fPGA均值、标准差与井下记录PGAR之间的关联性；建立场地特征参数Vs30、Vs20和覆盖层厚度D与fPGA之间的关系；研究fPGA的概率预测模型，进而提出场地条件校正的地表PGA 概率预测方法。

1 地震数据

日本国家地球科学与灾害预防研究所KiK-net强震观测台网在全日本范围内安装有近700个强震台站，每个台站的地表和井下分别安装三分量(NS和EW 两水平向以及一个竖向)加速度强震仪，分别记录地震中地表和井下的加速度时程。此外，每个台站均提供了场地钻孔资料，包括土层结构、土层剪切波速和纵波波速等信息。

本文对KiK-net 台站及数据记录选取的主要原则：1)台站场地含一类、二类、三类和四类场地[1]，剪切波速和覆盖层厚度范围尽可能宽；2)地震震级大于4.0；3)选取强震数据尽量丰富的台站，井下加速度峰值PGAR值分布范围尽可能广。

依据以上原则，共选取40个台站，整理1996年3月−2019年5月地震加速度记录33260条。选取的地震加速度记录进行基线校正，同时采用25 Hz低通滤波处理。

台站场地工程特征参数取Vs30、Vs20和场地覆盖层厚度D。各参数定义如下：近地表20 m 土层等效剪切波速值Vs20；近地表30 m 土层平均剪切波速值Vs30；地表至剪切波速大于500 m/s的土层顶面距离定义为D。图1显示选取的台站场地参数的统计分布图。从图1可以看出，所选台站场地的Vs30分布于100 m/s～1000 m/s，大部分场地的Vs30介于200 m/s～600 m/s；Vs20分布于100 m/s～800 m/s；覆盖层厚度的范围较广，大多数场地覆盖层厚度在50 m 以内，少数巨厚场地，覆盖层厚度在200 m 以上。根据我国的抗震设计规范场地分类标准，选取的台站中26个场地为二类场地，占总数的65%。说明：Vs30、Vs20和D根据KiK-net提供的台站土层信息计算得出，其中个别台站，如KSRH04、AOMH13和NMRH04，因其土层信息中剪切波速均小于500 m/s，D则取为台站地表和井下记录点间的厚度。

图1 选取台站场地特征参数统计分布Fig.1 Statistic histograms of site characteristic parametersof selected stations

2 地表PGA 放大系数f PGA

2.1 概率分布特征

研究场地PGA 放大系数的概率分布特征，首先定义PGA 放大系数fPGA为：

由于地表和井下加速度记录中均包含两个水平向时程，本文中加速度峰值取值为两水平向记录峰值的几何平均值，即：

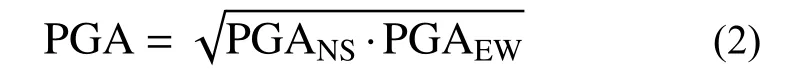
式中：PGANS为南北水平向加速度记录的峰值；PGAEW为东西水平向加速度记录的峰值。

探讨fPGA的分布规律，图2举例给出NMRH04台站记录的PGA 放大系数fPGA与井下记录PGAR的分布图。可以看出，给定PGAR情况下，fPGA具有一定的不确定性。首先，考虑给定PGAR情况下，fPGA的概率分布特征。鉴于记录数据分布的不均匀性以及单台数据量的限制，将台站记录数据按照井下PGAR值分为3个区间，即小震(<5 cm/s2)、中震(5 cm/s2～20 cm/s2)和大震(>20 cm/s2)，然后分别探讨区间内fPGA的分布特征。以NMRH04台站为例，图3显示该台站数据3 个区间内的fPGA频数直方图，灰曲线为对数正态分布函数拟合曲线。图4显示不同区间内，实测fPGA概率分布与对数正态分布理论概率曲线对比，二者吻合较好。给定PGAR情况下，NMRH04台站实测fPGA可采用对数正态分布函数模拟。其他台站的fPGA数据分析结果均表现出类似的规律。所以，建议采用对数正态分布概率密度函数来拟合fPGA数据。

2.2 概率模型

式中：x为给定井下PGAR下地表PGA 放大系数fPGA值；λ 为fPGA的对数均值；ζ 为fPGA的对数标准差。确定式(3)的关键是计算λ 和ζ。根据数学统计学方法，对数概率分布的均值和方差可以由下面公式计算得出，

图2 台站NMRH04实测f PGA 随着井下PGAR 的散点图Fig.2 Scattering of recorded f PGA distribution with PGAR for station NMRH04

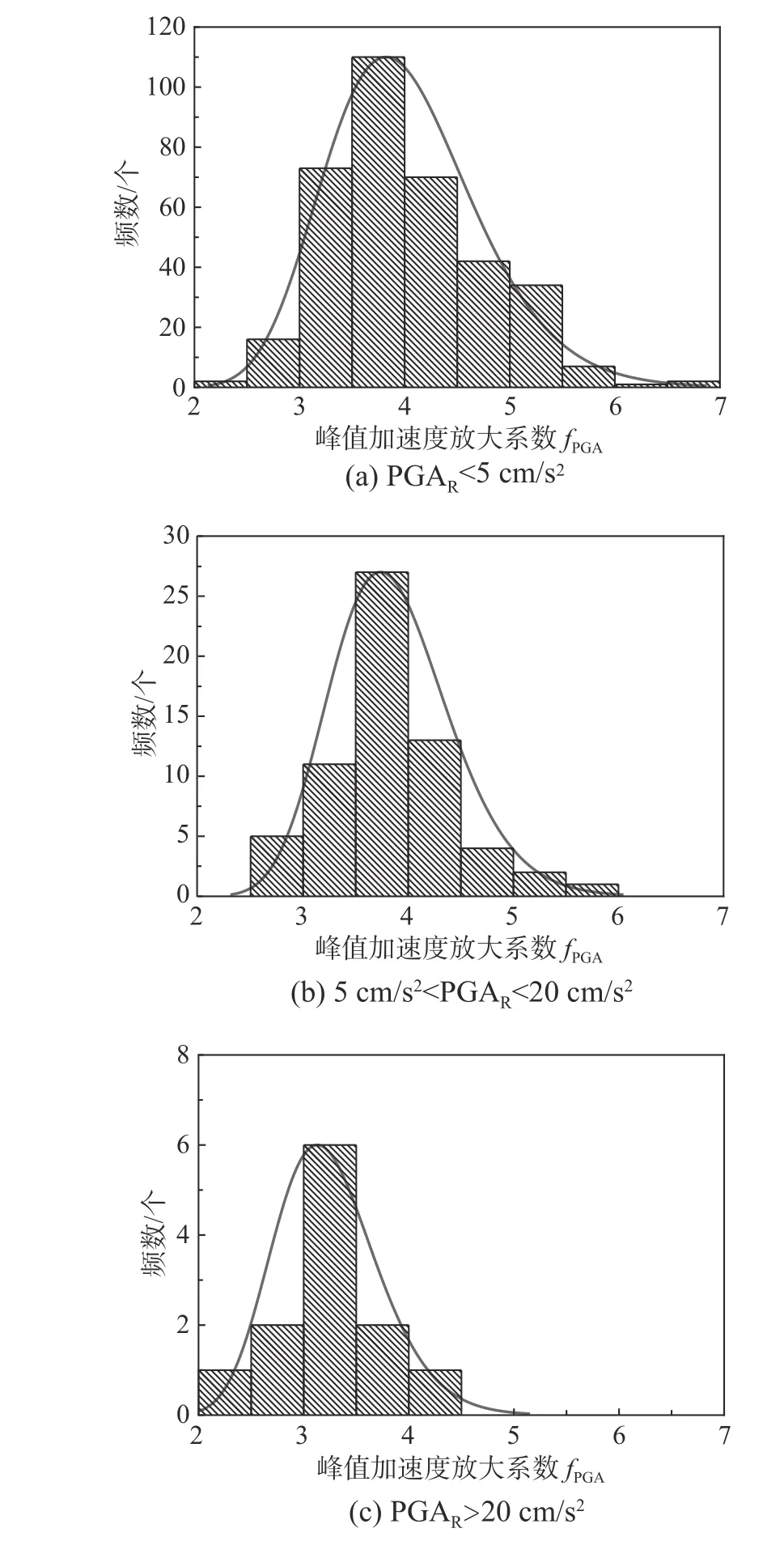
图3 NMRH04台站数据分组区间的f PGA 频数统计分布Fig.3 Frequency distribution of f PGA values of NMRH04 in different PGAR bins compared with log-normal distribution curves

图4 NMRH04台站数据分组区间的f PGA 概率分布与理论对数正态分布对比Fig.4 Testing distribution of f PGA values of NMRH04 in different PGAR bins using a log-normal distribution model

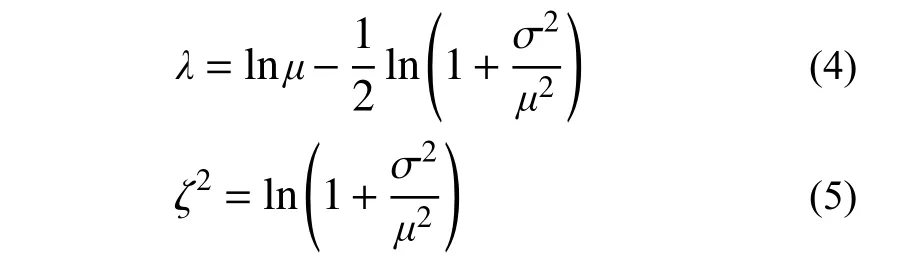
式中，µ和σ 为fPGA数据样本的均值和标准差。

由于数据点空间分布的不均匀性，根据PGAR值，将数据进行分组。为建立µ(fPGA)及σ(fPGA)与PGAR的经验关系，这里的分组更加细化，主要分组原则：1)当输入PGAR<10 cm/s2时，每2 cm/s2分为一组；2)当PGAR>10 cm/s2<30 cm/s2时，每4 cm/s2分为一组；3)当PGAR>30 cm/s2时，分为一组。需要注意的是，当某一组内的数据点小于3个时，应与其相邻区间数据点较少者合并；但若相邻区间的数据点相同，则与上一区间合并。根据PGAR分区间内fPGA的数据样本，得到每个区间的fPGA的均值和标准差，记为µ(fPGA)和σ(fPGA)。图5显示FKSH12台站µ(fPGA)-PGAR和σ(fPGA)-PGAR分布图。由图5可以看出，FKSH12台站数据的µ(fPGA)和σ(fPGA)随着输入PGAR的增大呈减小的趋势。其他台站记录分析结果表现出类似特征。

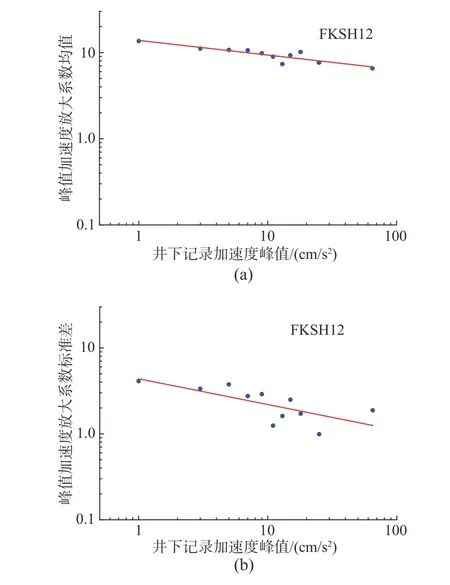
图5 FKSH12台站场地f PGA 的均值和标准差与PGAR 拟合关系Fig.5 Linear fitting of means and standard deviations of f PGA with respect to PGAR for station FKSH12

由于土层在地震作用下的非线性，fPGA与地震动强度有关。以井下记录的PGAR表征输入地震动强度，以往研究[23− 24]显示fPGA均值与PGAR的关系可以通过对数线性或者对数二次函数进行拟合。简化起见，本文采用自然数坐标系下线性拟合，即：

其中，a1、b1和a2、b2为待定拟合系数(以下简称拟合系数)，与场地特征相关，可以通过对数据的回归分析得到，如图5中斜线为线性拟合的结果。

2.3 概率模型参数的确定

通过对台站记录地震数据回归拟合可以得到式(6)和式(7)中的拟合参数，见表1。从表中可以看出，不同台站之间拟合系数存在一定的差异性，其主要由场地特性的差异性所导致。下面建立式(6)和式(7)的拟合系数与场地特征之间的关联性。场地特征参数选取场地常用的工程参数，即Vs30、Vs20和覆盖层厚度D。图6～图8显示四个拟合参数分别与Vs30、Vs20和D关系的散点图。由图中看出，拟合系数与Vs30、Vs20和D相关性不明显，说明单一参数无法估计拟合系数。

场地剪切波速和覆盖层厚度是反映场地地震反应的两个重要参数指标，放大系数理应与剪切波速与覆盖层厚度存在一定的关联性。采用数据挖掘的方法，尝试建立拟合系数与场地特征参数线性组合的关联性，即Vs30、Vs20和D的线性组合，

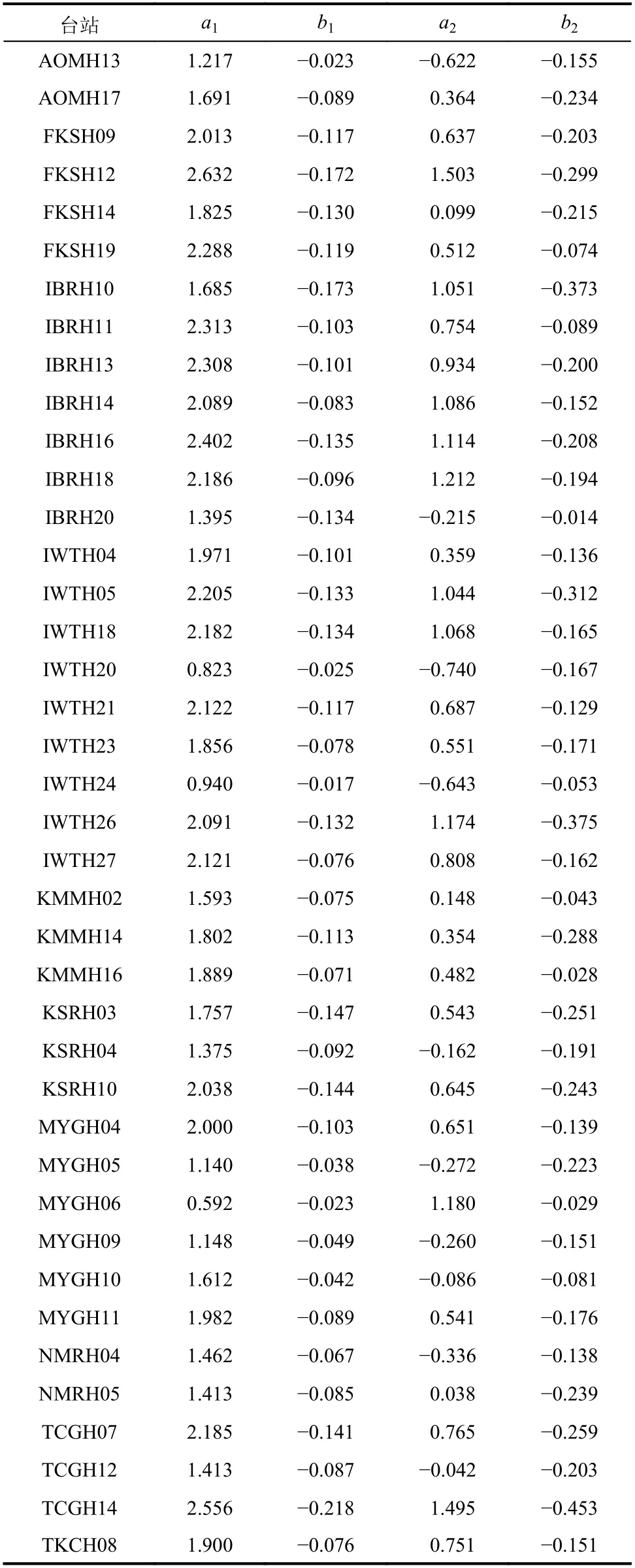
表1 选取台站场地f PGA 拟合系数值Table 1 Regressive coefficients of f PGA for selected stations

图6 拟合系数与V s30 的关系散点图Fig.6 Scattering of regressive coefficients with respect to V s30

图7 拟合系数与VS20的关系散点图Fig.7 Scattering of regressive coefficients with respect to VS20

图8 拟合系数与D 的关系散点图Fig.8 Scattering of regressivecoefficientswith respect to D

式中，a、b、c为待定系数。分别采用线性和二次函数的形式建立式(6)和式(7)的拟合系数与场地特征参数组合Zi(i=1,2,3,4)之间的关系，即：

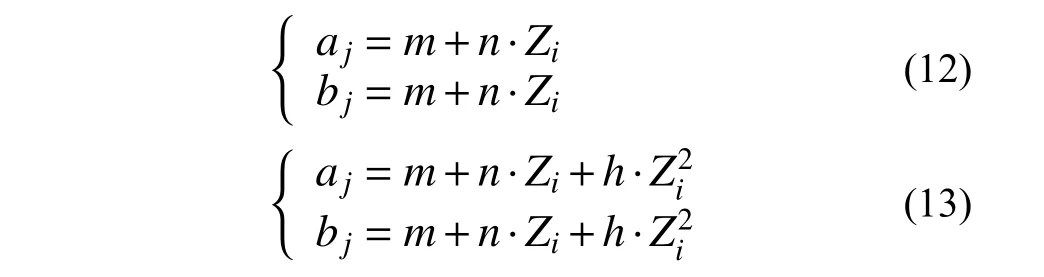
其中，j=1,2。表2给出了对实测数据进行线性回归得到的各待定系数以及残差平方和。图9～图16显示拟合结果与实测数据的对比，其中直线或者曲线为拟合曲线，散点为实测数据值。相对于图6～图8，图9～图16显示的拟合系数与场地特征参数线性组合相关性较好。根据表2中残差平方和大小，发现Z1与Z4的组合与拟合系数相关性最大，而且二次函数拟合比线性拟合结果稍好。

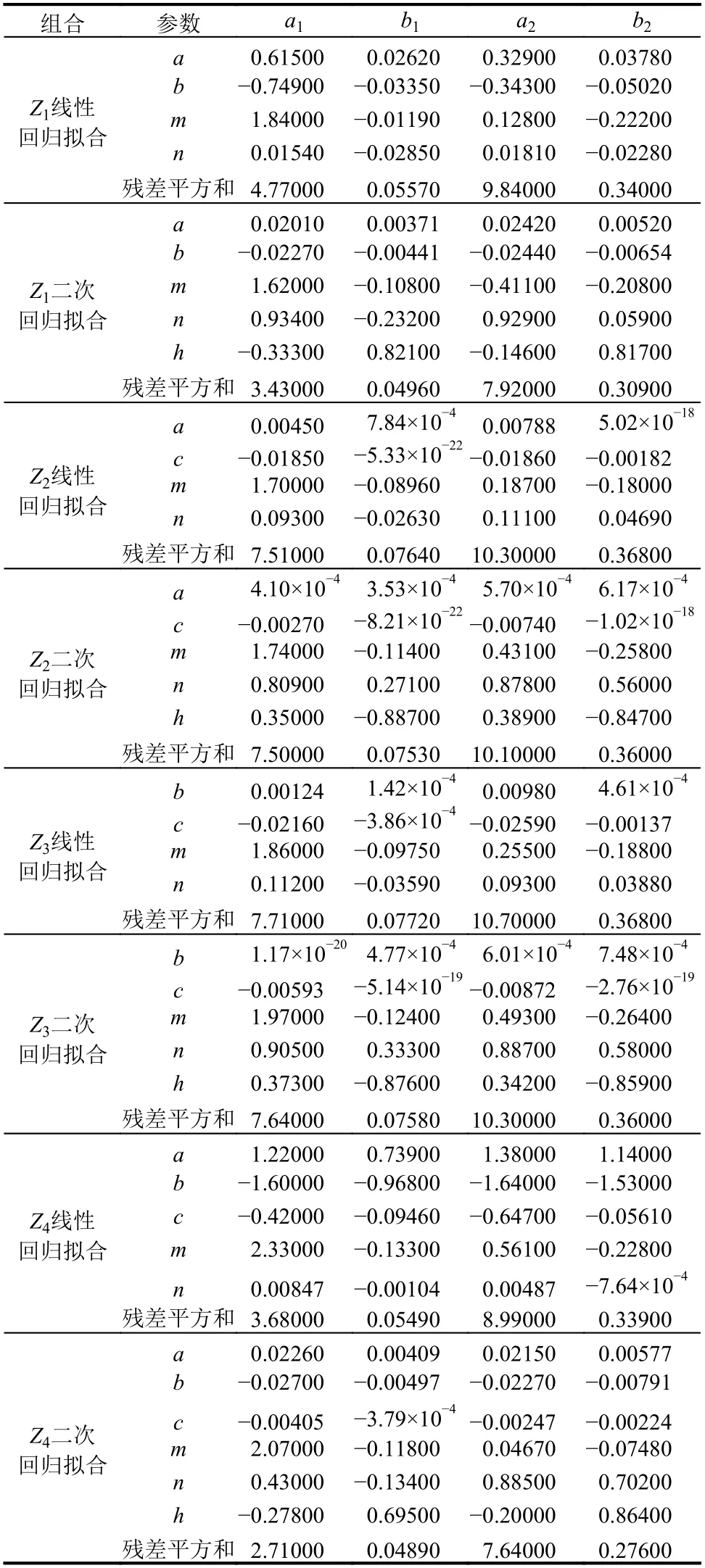
表2 场地特征参数线性组合Z1～Z4 下实测数据拟合得到的待定系数值Table2 Coefficientsof regressive parametersobtained by regressing on seismic data with respect to linear combinations of site characteristic parameters Z1～Z4

图9 拟合系数与Z1线性拟合结果与实测数据对比Fig.9 Linear fitting of regressivecoefficientswith Z1 comparing to recorded data

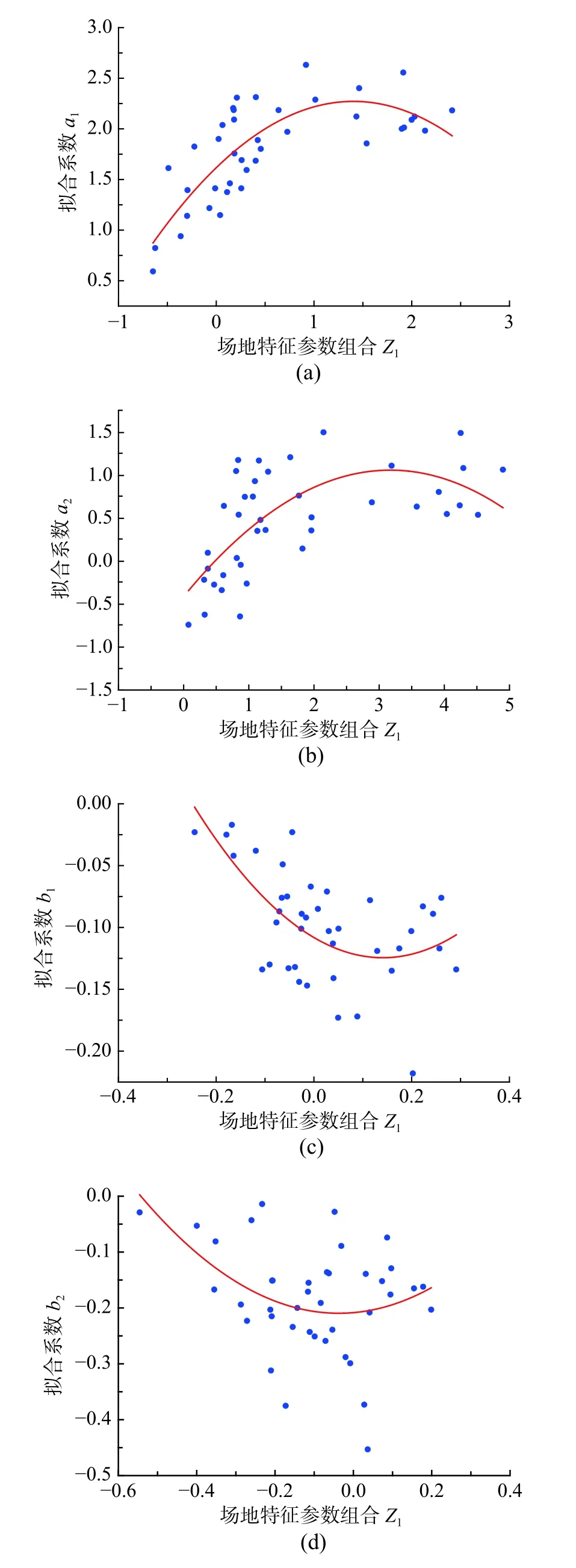
图10 拟合系数与Z1二次函数拟合结果与实测数据对比Fig.10 Quadratic fitting of regressive coefficients with Z1 comparing to recorded data

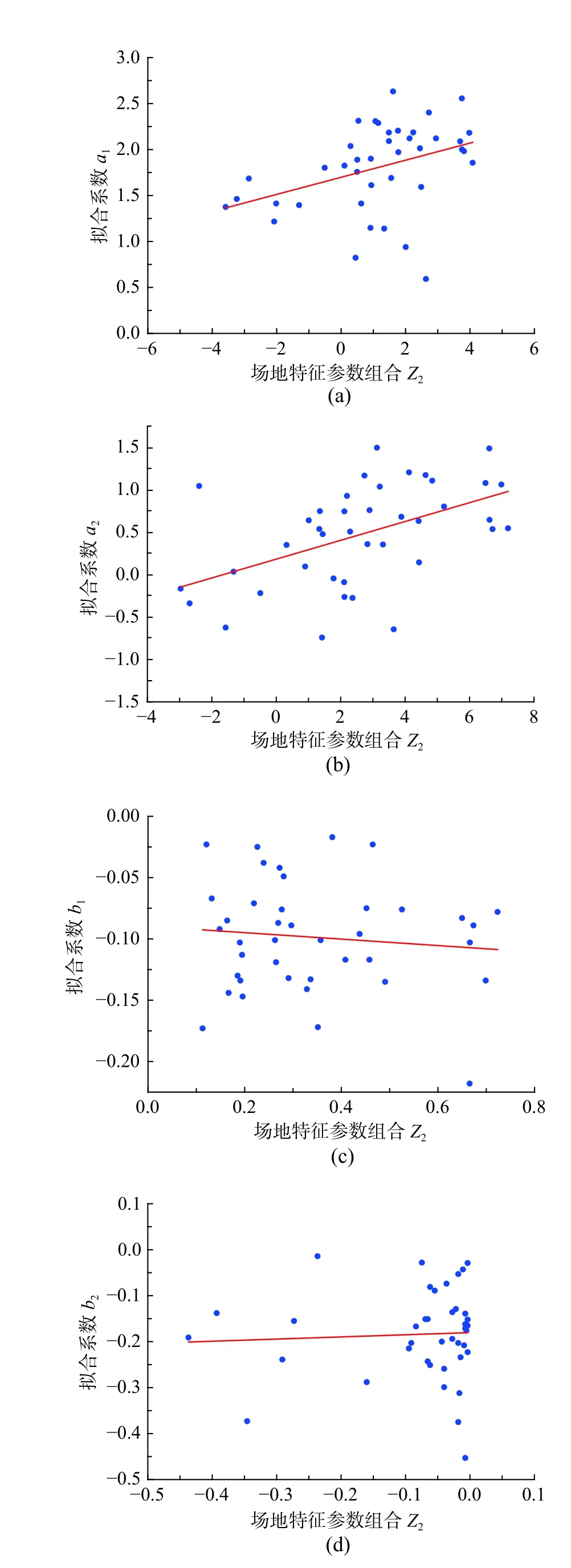
图11 拟合系数与Z2线性拟合结果与实测数据对比Fig.11 Linear fitting of regressive coefficients with Z2 comparing to recorded data

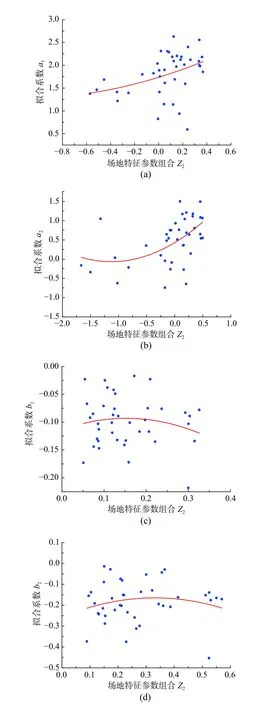
图12 拟合系数与Z2 二次函数拟合结果与实测数据对比Fig.12 Quadratic fitting of regressive coefficients with Z2 comparing to recorded data

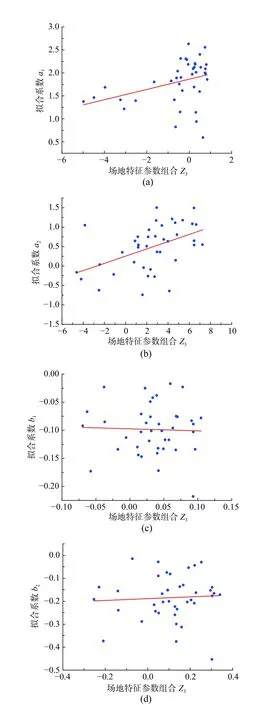
图13 拟合系数与Z3线性拟合结果与实测数据对比Fig.13 Linear fitting of regressive coefficients with Z3 comparing to recorded data

图14 拟合系数与Z3二次函数拟合结果与实测数据对比Fig.14 Quadratic fitting of regressive coefficients with Z3 comparing to recorded data

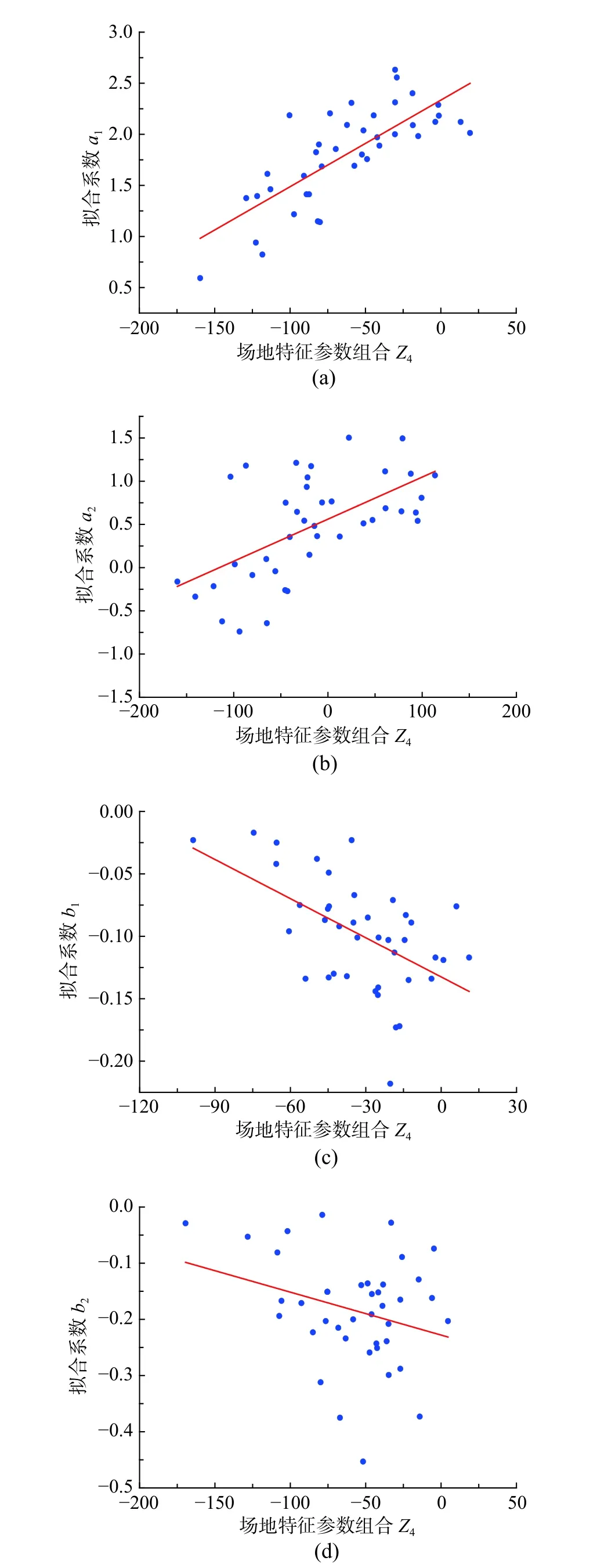
图15 拟合系数与Z4线性拟合结果与实测数据对比Fig.15 Linear fitting of regressive coefficients with Z4 comparing to recorded data

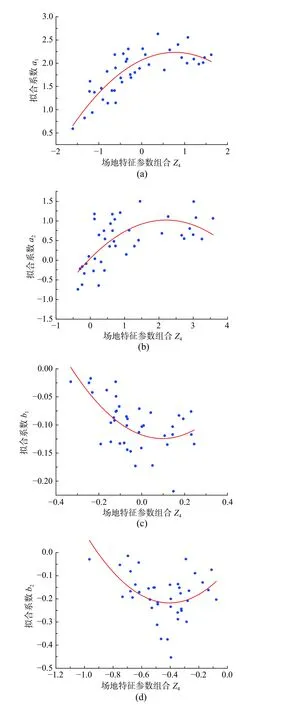
图16 拟合系数与Z4 二次函数拟合结果与实测数据对比Fig.16 Quadratic fitting of regressive coefficients with Z4 compared to recorded data

3 场地地表PGA概率预测

通过前文研究给出了fPGA均值、标准差估算式，并建立了拟合系数与场地特征参数之间的关联性。这种关联性可以通过场地特征参数的线性组合近似表达，但其物理意义尚需进一步明确。

将式(6)和式(7)得到的均值和标准差带入式(4)和式(5)，得到fPGA概率密度函数的均值和方差，代入式(3)即可得到fPGA概率密度函数。这样，在给定地震动输入强度PGAR下，通过式(3)可以得到不同概率水平下地表PGA 放大系数fPGA，与PGAR值乘积即可得到不同概率水平下地表PGA 预测值。图17显示计算不同概率水平下地表PGA 的流程框图，结合表2中得到待定参数估计值，可以预测不同概率水平下地表PGA。

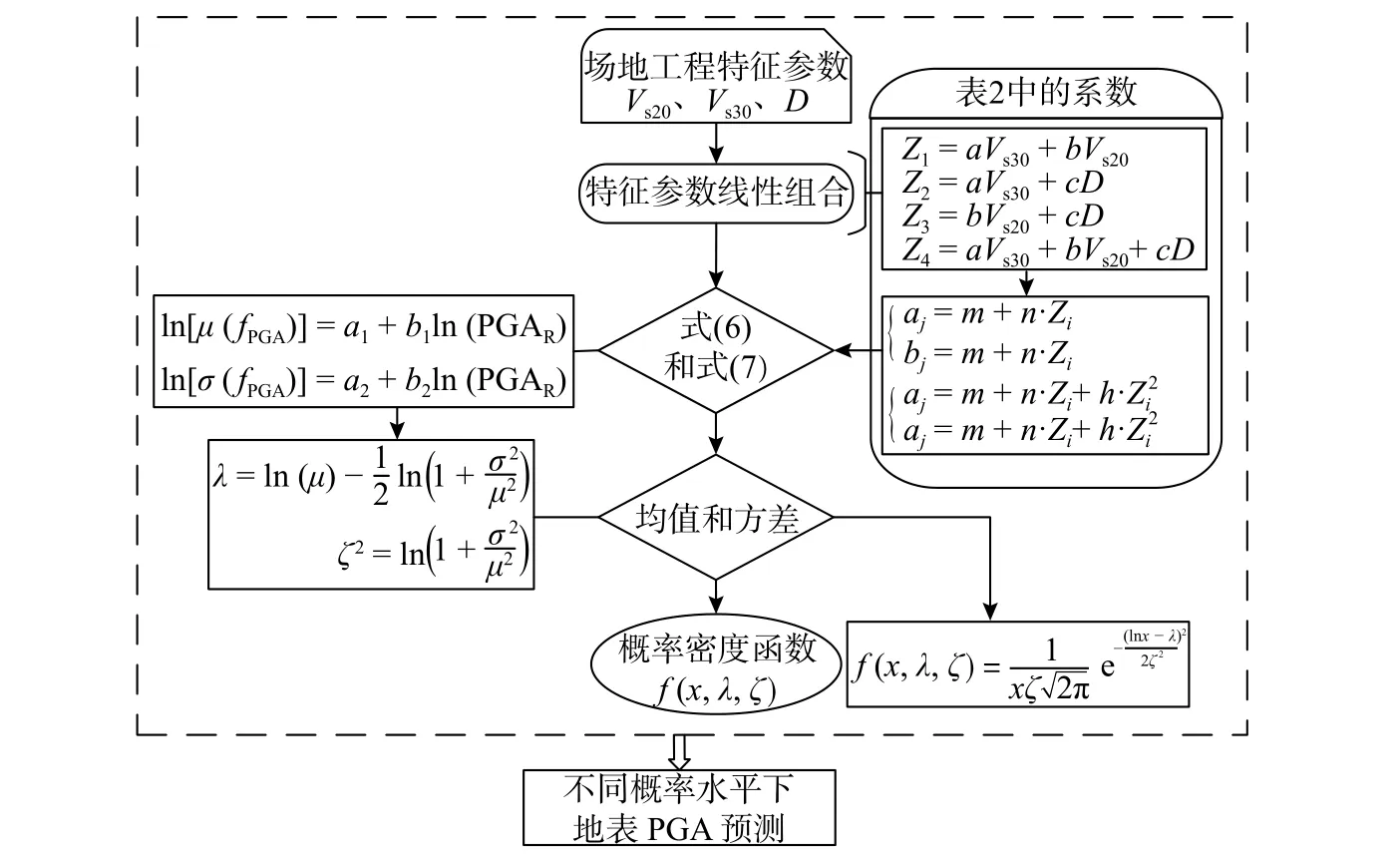
图17 不同概率水平下地表PGA 预测方法计算框图Fig.17 Flow chart for predicting surface PGA under different probability levels

为检验方法的可行性，这里以场地特征参数组合Z1和Z4为例，按照图17的计算流程，分别计算地表PGA 不同概率水平的预测结果，并与实测记录进行对比。这里的超越概率P定义为：实测PGA 值超过预测值的概率或可能性。限于篇幅，这里仅给出AOMH13、NMRH04、KMMH16和IWTH20四个台站预测结果与实测值的对比(图18和图19)。从图中可以看出，本文所提出的概率计算方法能够较合理地预测不同概率水平下地表PGA 值。然而，图18 和图19的预测结果尚存一定局限，主要是实测数据库中强震数据较少，PGAR多集中在50 cm/s2以下，导致不同概率水平下地表PGA 预测差别不明显。这一点可通过数值模拟补充，未来研究通过数值模拟增加大震计算工况，以弥补数据分布不均的缺陷。

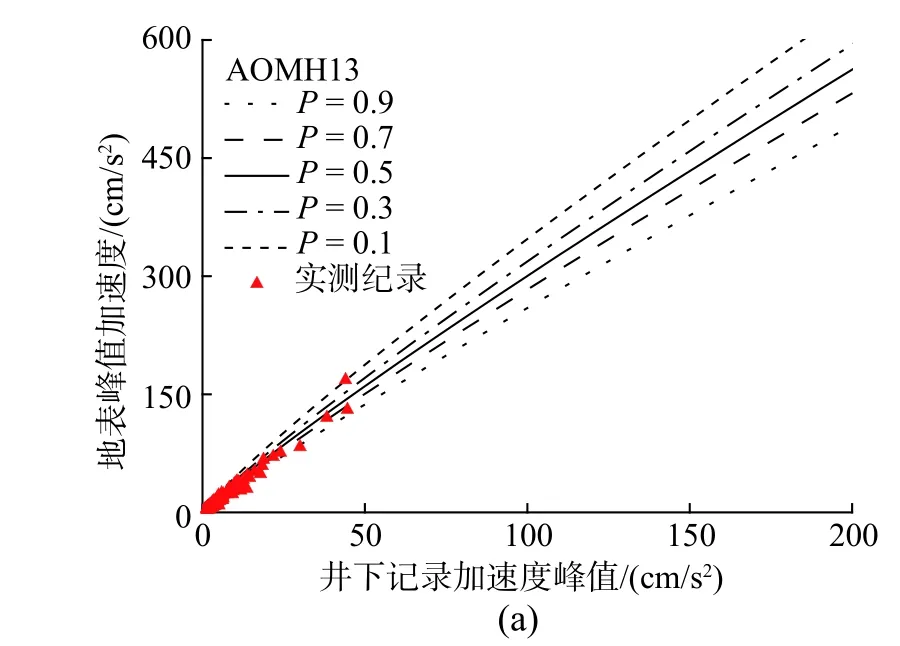
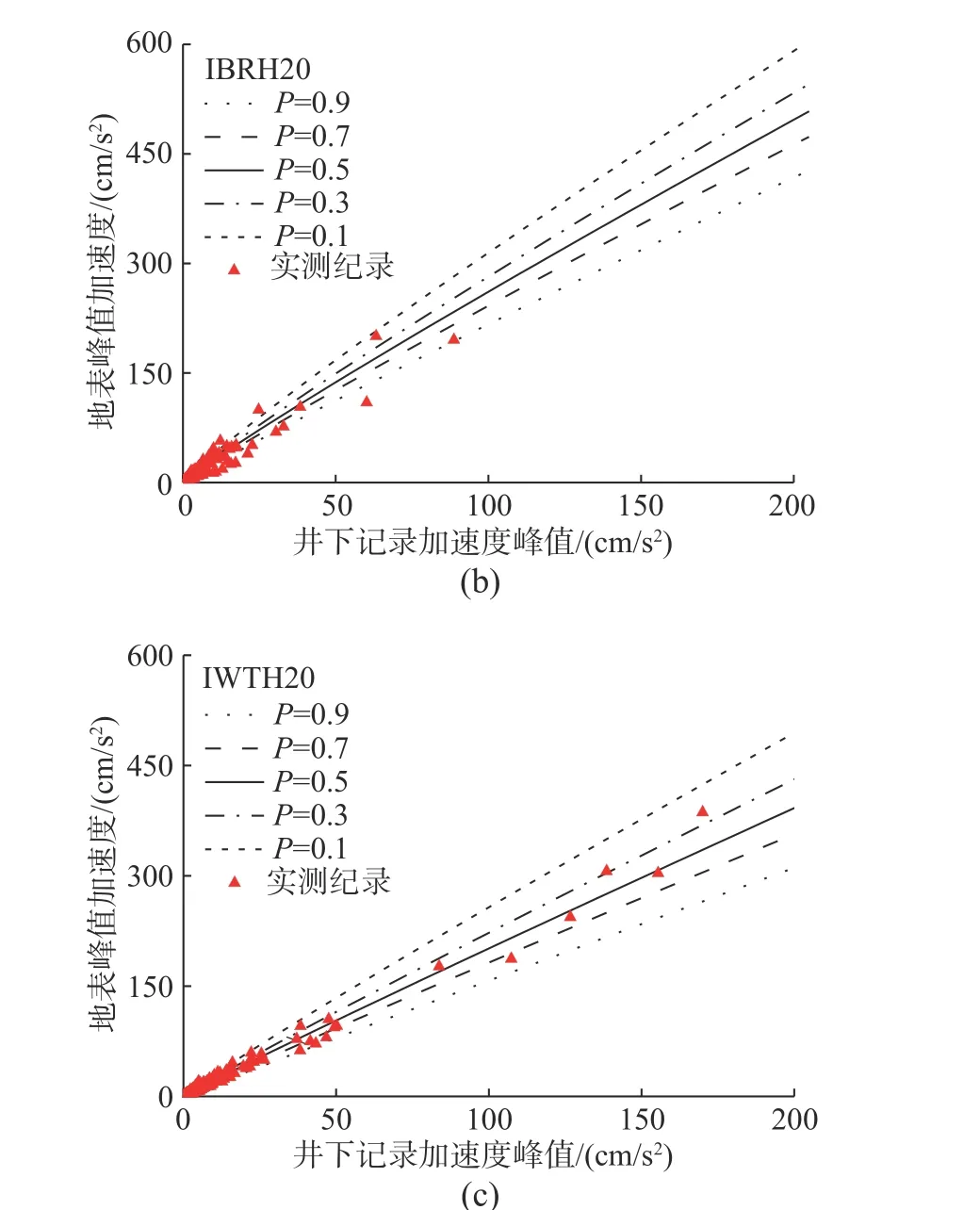
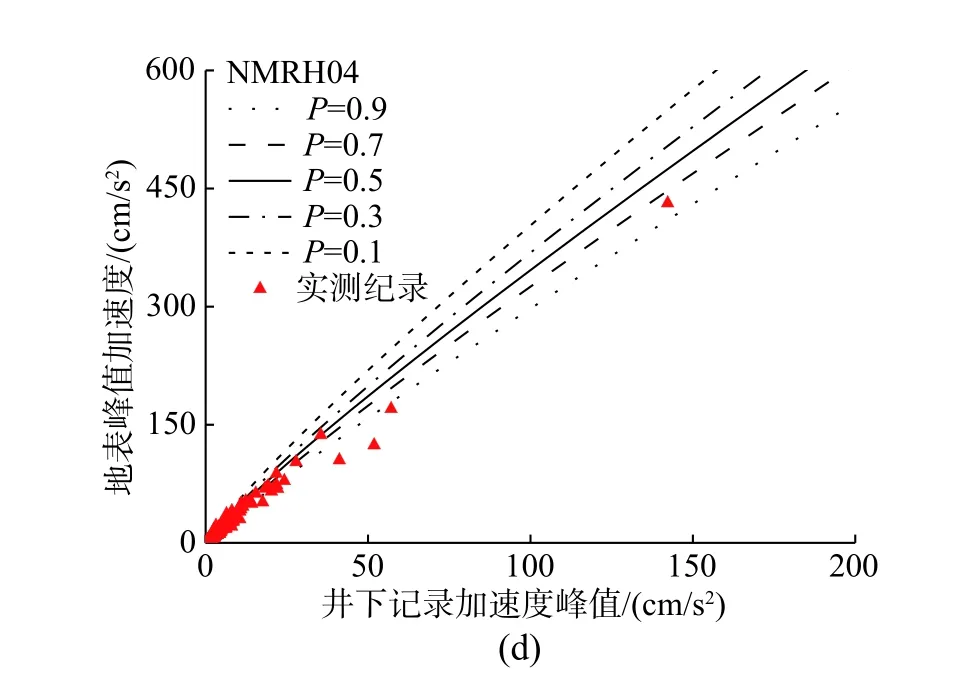
图18 场地特征参数Z1组合下不同超越概率水平预测地表PGA 值与实测数据的对比Fig.18 Predicted surface PGA under different probability levels with respect to Z1 comparing to observed data.

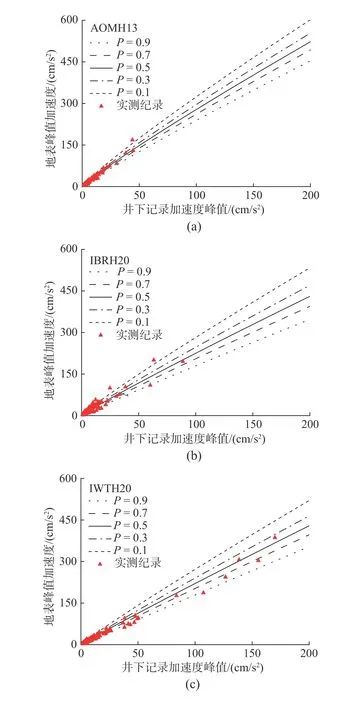
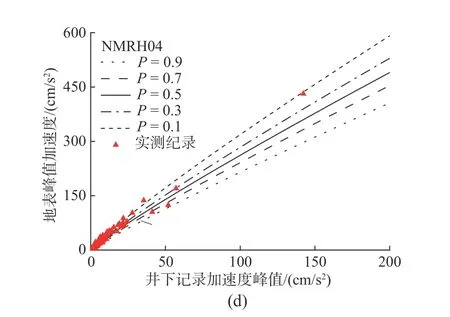
图19 场地特征参数Z4组合下不同超越概率水平预测地表PGA 值与实测数据的对比Fig.19 Predicted surface PGA under different probability levelswith respect to Z4 comparing to observed data.

4 结论

本文选取KiK-net 台网中的40个台站，搜集台站历史地震记录，含地表和井下加速度时程数据。通过实测数据分析，研究场地PGA 放大系数fPGA的概率分布特征，指出fPGA可以通过对数正态分布函数进行模拟，其概率分布参数(即均值和标准差)与场地特征参数线性组合之间存在一定的关联性，这种关联性可以通过场地特征参数线性组合近似确定，并给出参数估计值，可为地震预警中不同概率水平下，PGA 预测提供一种可行的途径。主要工作及结论概括如下：

(1)鉴于土层特性的复杂性，工程场地PGA 放大系数fPGA具有不确定性，研究发现在一定地震动强度输入情况下，fPGA基本服从对数正态分布，其均值和方差与场地特征相关。

(2)场地的工程参数Vs30、Vs20和场地覆盖层厚度D单独与fPGA之间相关性较小，而这些特征参数的线性组合与fPGA之间具有一定相关性。通过数据挖掘，建立了场地Vs30、Vs20和D的线性组合与fPGA之间关系，便于估计fPGA值。

(3)通过fPGA概率模型，给出多概率水平下地表PGA 的预测，通过实测数据检验，本文建立的PGA 概率预测模型具有一定的可行性。

(4)随着风险评估等概念在工程上实施，可接受风险水平成为决策者决策的重要依据，本文就是在这一思想的框架下，面向地震预警的地表PGA 预测提出一种可行的概率方法，为地震预警及烈度速报技术中PGA 估计的场地校正技术提供一种途径。