基于双变量降维模型和Kriging近似的统计矩点估计法

范文亮，袁 满，刘润宇，杨晓阳，李正良

(1.重庆大学土木工程学院，重庆400045；2.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆400045)

点估计法[1−3]是随机系统常用分析方法，其计算简便有效且可直接与矩方法结合进行结构可靠度分析[4−5]。点估计法中多维数值积分不可避免，往往遭遇维数灾难问题。高效的选点策略与降维近似是目前常用的缓解维数灾难的方法。基于稀疏点集的点估计法[6]是高效选点策略中具有相对较广适用范围与较高精度的方法，但对于交叉项影响较显著的情形精度会有所减弱[6−7]。文献[8]的比较研究表明将多维函数近似为一系列较低维数分量函数组合的降维近似模型在有效缓解维数灾难的同时可保持较好的精度。因此，近年来基于降维近似模型的统计矩估计引起了广泛的关注。对于一个多变量函数，通常可有乘积降维近似[9−10]和加和降维近似[11]两种策略。Rosenblueth[2]首先引入了单变量乘积降维近似模型计算了多变量函数的统计矩。多变量乘积降维近似中，由于具有相同变量的分量函数通过累乘组合在一起，其多维积分并不能转化为低维积分，因此，除单变量乘积降维近似模型外，鲜有乘积降维近似模型用于统计矩估计；然而，随着随机系统维数的增加，单变量乘积降维近似模型并不能保证合理的精度。相比较而言，加和降维近似模型中，分量函数通过加和的方式相组合，其多维积分必定可转化为一系列的低维积分，因此，加和降维近似模型在统计矩估计中应用更为广泛。Zhao等[12]首先将多变量函数的单变量降维近似模型用于统计矩估计；随后Rahman 等[13]亦提出了基于单变量降维近似模型的统计矩估计方法，并对单变量降维近似模型进行了详细的理论分析；李洪双等[14]采用了在文献[13]的基础上引入了Nataf 变换，拓展了其适用范围。由于仅涉及到多个单变量函数的概率积分，基于单变量降维近似模型的点估计法具有极高的计算效率，然而对于交叉项作用较复杂随机系统，其精度亦不够理想。为改善精度，Xu 等[15]进一步提出了针对矩函数进行降维多变量加和降维近似的统计矩估计方法；Huang 等[16]和Yu 等[17]将矩函数的双变量降维近似分别与Rosenblatt 变换和Nataf 变换相结合，发展了较为实用的统计矩估计方法。相比于矩函数，原函数更为简单，Fan 等[18]提出了针对原函数采用多变量加和降维近似的直接积分法，在不增加计算量的基础上，进一步提高了统计矩估计的精度。不难发现，随着降维近似模型截断维数的增加，模型的精度会逐步改善，但分量函数会逐步增多，进而导致计算量激增。因此，将截断维数取为2是兼顾精度和效率的实用选择[16−18]。然而，即使对于双变量加和降维近似模型，一旦随机系统的维数较高，双变量分量函数将急剧增加，其计算效率并不总是很理想。事实上，双变量分量函数的积分中，各积分点的权重系数是不同的，若允许权重较小的计算点的响应存在一定的误差，则可针对分量函数引入较为成熟的代理模型以改善计算效率。

为此，本文基于函数近似和数值积分中求积节点的特性，提出了Kriging 近似模型训练点集确定的“米”字型策略，并基于此建立了双变量分量函数的Kriging 近似，将其与现有的基于双变量降维近似模型的统计矩估计方法相结合，建立了更为高效的统计矩点估计法。

1 基于双变量降维近似模型的统计矩点估计法

通常，基于双变量降维近似模型的统计矩计算包括三个步骤：1)将分布类型不同的随机变量X向独立标准正态空间转换，得到新的随机向量U=(U1,U2,···,Un)T和响应函数h(U)；2)利用双变量降维近似模型将多维响应函数分解为二维及以下分量函数的线性组合；3)基于双变量降维近似模型进行响应函数的统计矩计算。

1.1 变量的独立化正态变换

随机向量X中的变量概率信息(如分布类型和相关信息等)常常不同，在随机分析和可靠度分析中常将随机向量X向独立标准正态空间转换，得到新的随机向量U=(U1,U2,···,Un)T。于是，响应函数Z=g(X)可改写为：

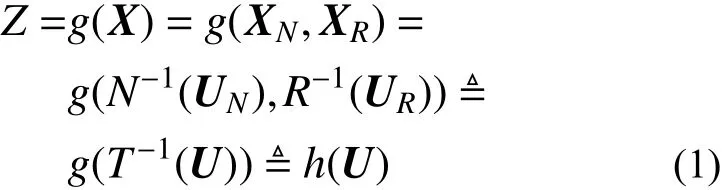
式中：X R为X中已知联合概率分布的变量组成的向量；XN为剩余变量组成的向量，既包括独立变量，亦包括已知边缘密度函数和相关信息的变量；U={UN,UR}。N−1(·)、R−1(·)分别表示Nataf 变换[19]与Rosenblatt 变换[20]的逆变换。

1.2 基于双变量降维近似模型的统计矩估计

由概率论可知，随机响应函数Z的b阶统计矩矩MZ,b的表达式如下：

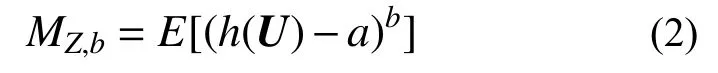
式中，当b=1时，a=0，MZ,1表示响应函数的均值；当b>1时，a=MZ,1，MZ,b为响应函数的b阶中心矩。

根据降维近似的对象不同，基于双变量降维近似模型的统计矩估计可以分为两类：1)基于矩函数[h(U)−a]b的双变量降维近似模型的统计矩估计；2)基于原函数h(U)的双变量降维近似模型的统计矩估计。

1.3 基于矩函数双变量降维近似模型的统计矩估计

若引入[h(U)−a]b的双变量降维近似模型，并进行期望运算，可给出MZ,b的近似计算表达式如下[16]：

1.4 基于原函数双变量降维近似模型的统计矩估计

若先引入h(U)的双变量降维近似模型，然后再对[h(U)−a]b进行期望运算，可给出MZ,b的另一种近似计算表达式[18]：

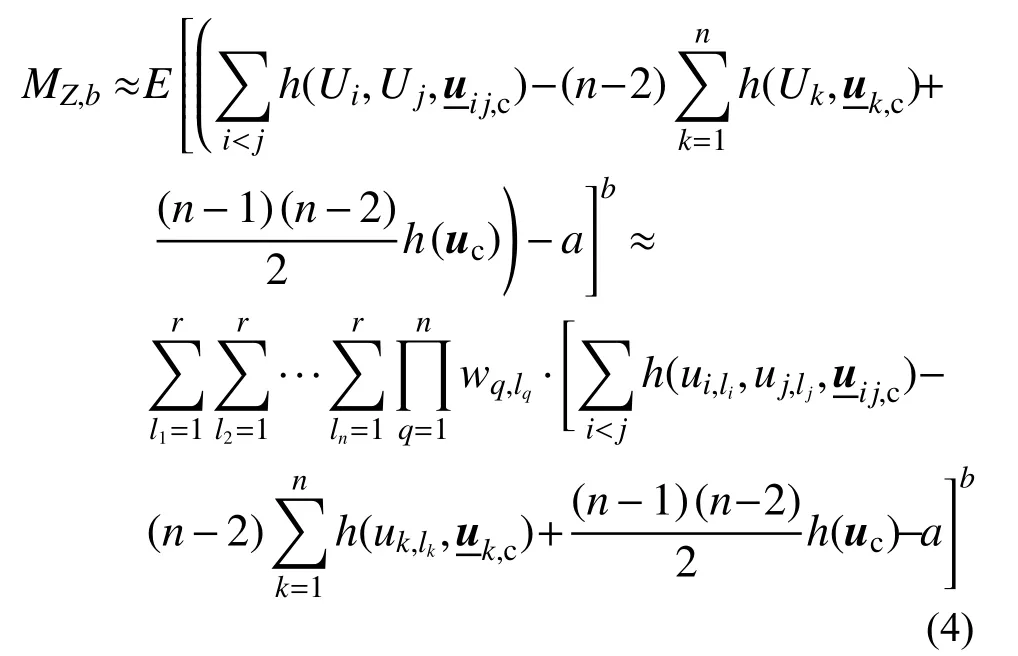
为简便，该方法记为N-2。

2 改进的双变量降维近似统计矩估计

在双变量降维近似统计矩估计中，无论是D-2方法还是N-2方法，其计算量主要体现于双变量分量函数在积分节点处的函数值计算，对于隐式的g(X)，其函数值需通过结构分析获得。实用中，通常取r=7，则任一双变量分量函数均涉及7×7=49次的结构分析。若能在保持计算精度相当的前提下减少原函数的调用次数，则可以有效改善计算效率，较好地兼顾精度和效率的平衡。

事实上，在双变量分量函数的49个求积节点中，权系数的差异较为明显，权系数较小节点的函数值即使存在着一定的误差，总体计算结果的误差仍是可以接受的。为此，本文将任一双变量分量函数的49个求积节点分为计算节点和近似节点，其中计算节点的函数值通过函数调用或结构分析获得，近似节点的函数值则由基于计算节点确定的双变量分量函数的近似模型计算得到，此处近似模型采用Kriging 模型。由于近似节点的函数值不再涉及原函数调用或结构分析，将有效改善计算效率。

2.1 Kriging 近似模型

2.2 改进的双变量降维近似统计矩估计

2.2.1双变量分量函数的Kriging 模型

1)计算节点的选取策略

图1(a)给出了以标准正态密度函数为权函数的二维高斯求积分公式的49个积分节点，记为集合DOE。理论上，定义域内任意点皆可以作为Kriging 模型的训练点集，即计算节点。然而，统计矩估计中仅需要双变量分量函数在49个积分节点的函数值，因此，计算节点可在此49个节点中选取，且应遵循如下准则：

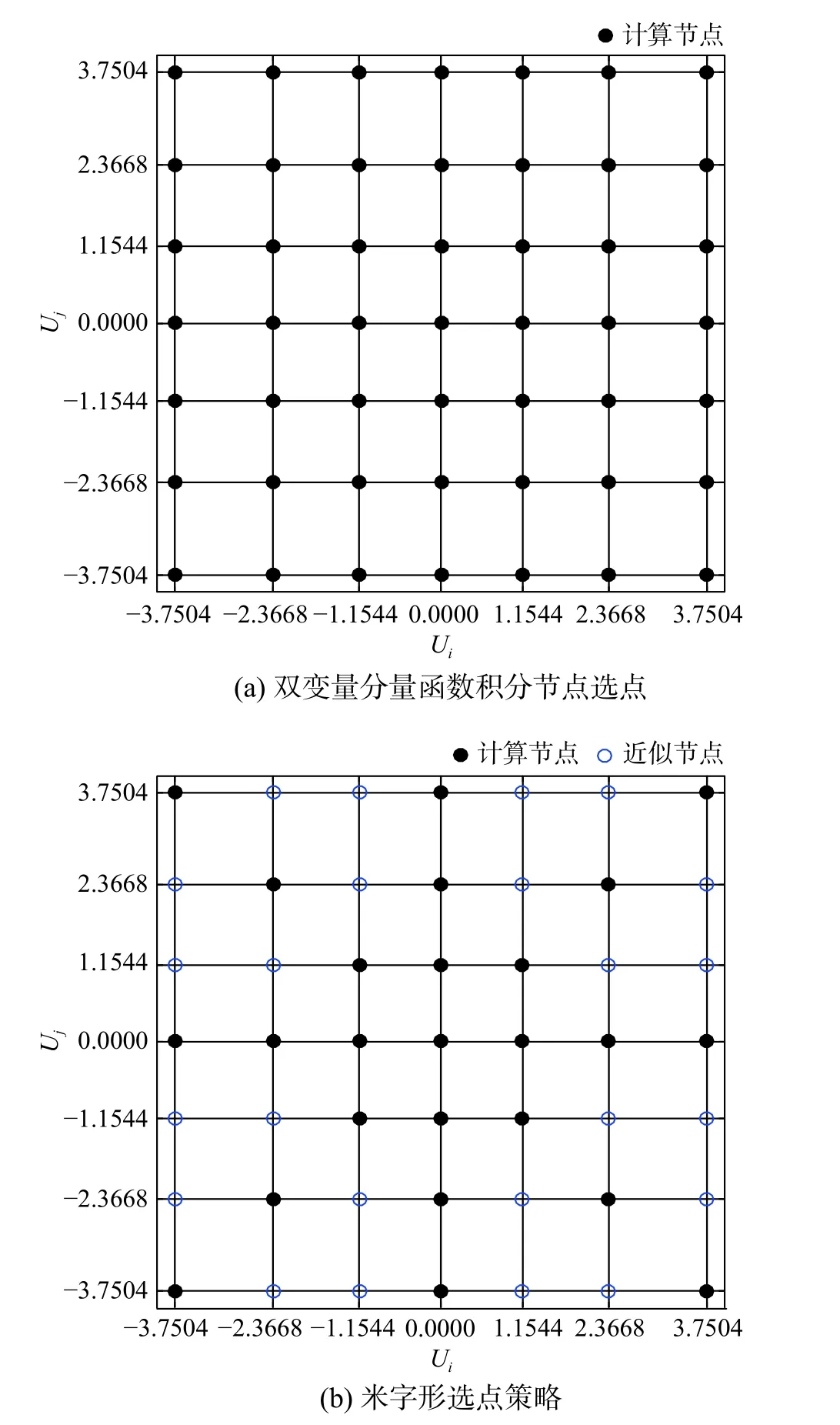
图1 选点方案示意图Fig.1 Schematic diagram of point selection

①具有较大权系数的计算节点函数值误差对整体积分的影响往往较大，因此计算节点优先选择权系数较大的积分节点，换言之，计算节点应尽量靠近中心区域；

②函数近似中，内插精度往往高于外插精度，因此计算节点应包含一定的外围节点；

③当涉及对称型分布的随机变量，其参考点坐标分量为0，二维积分节点中的轴点和一维积分节点重合，为充分利用这些节点，计算节点宜优先选择轴点。

2)双变量分量函数的Kriging 近似

首先，针对集合DOEY中所有的计算节点u0，通过调用函数或结构分析确定双变量函数h(Ui,Uj,u ij,c)

2.2.2改进的双变量降维近似统计矩估计

相应于常规的基于双变量降维近似模型的统计矩估计，结合双变量分量函数Kriging 近似的改进统计矩估计亦分为两类：基于矩函数双变量降维和Kriging 近似的统计矩估计、基于原函数双变量降维和Kriging 近似的统计矩估计。

基于上述考虑，本文给出的计算节点选取方案如图1(b)所示。为简便，可将计算节点的集合记为DOEY，其形状呈“米”字形，故称为“米”字形策略。

1)基于矩函数双变量降维和Kriging 近似的统计矩估计

将式(14)得到的双变量分量函数的Kriging 近似代入式(3)，可得到改进的基于矩函数双变量降维近似模型的统计矩估计：

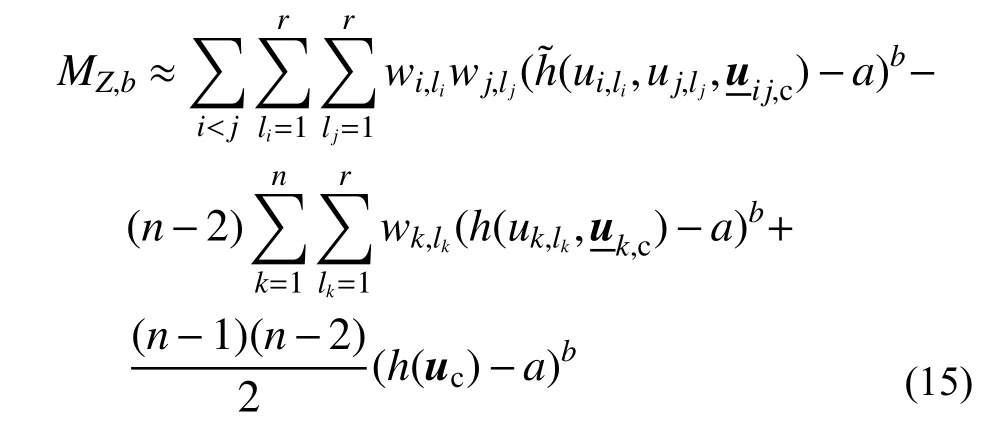
为简便，该方法记为米D-2。

2)基于原函数双变量降维和Kriging 近似的统计矩估计

将式(14)得到的双变量分量函数的Kriging 近似函数代入式(4)中，可得到改进的基于原函数双变量降维近似模型的统计矩估计，其表达式如下：

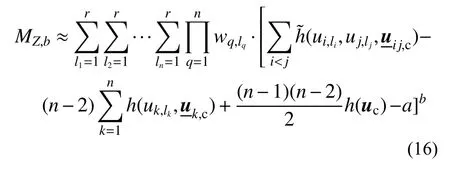
为简便，该方法记为米N-2。

不难发现，与D-2、N-2方法相比，米D-2和米N-2方法亦充分考虑了交叉项的影响，只不过是真实双变量分量函数被合适的Kriging 函数近似代替。

2.3 算法步骤

综合上述过程，改进的双变量降维近似统计矩估计实现过程如下：

1)根据已知概率分布信息，由式(1)将随机向量X转化为标准正态向量U。

2)确定各双变量分量函数在计算节点处的函数值，并基于此由式(14)确定各双变量分量函数的Kriging 近似。

3)确定各单变量分量函数在求积节点处的函数值，由各双变量分量函数的Kriging 近似确定其在二维积分节点的函数值，将上述函数值以及参考点处的函数值代入式(15)或式(16)即可得到响应Z的b阶统计矩。

3 算例分析

式中：X1为对数正态分布变量，均值为22、标准差为2；X2为正态分布变量，均值为10、标准差为0.9；X3为极值I型变量，均值为2、标准差为0.6。

对于上述三变量函数，参考点为uc=T−1(µX)=

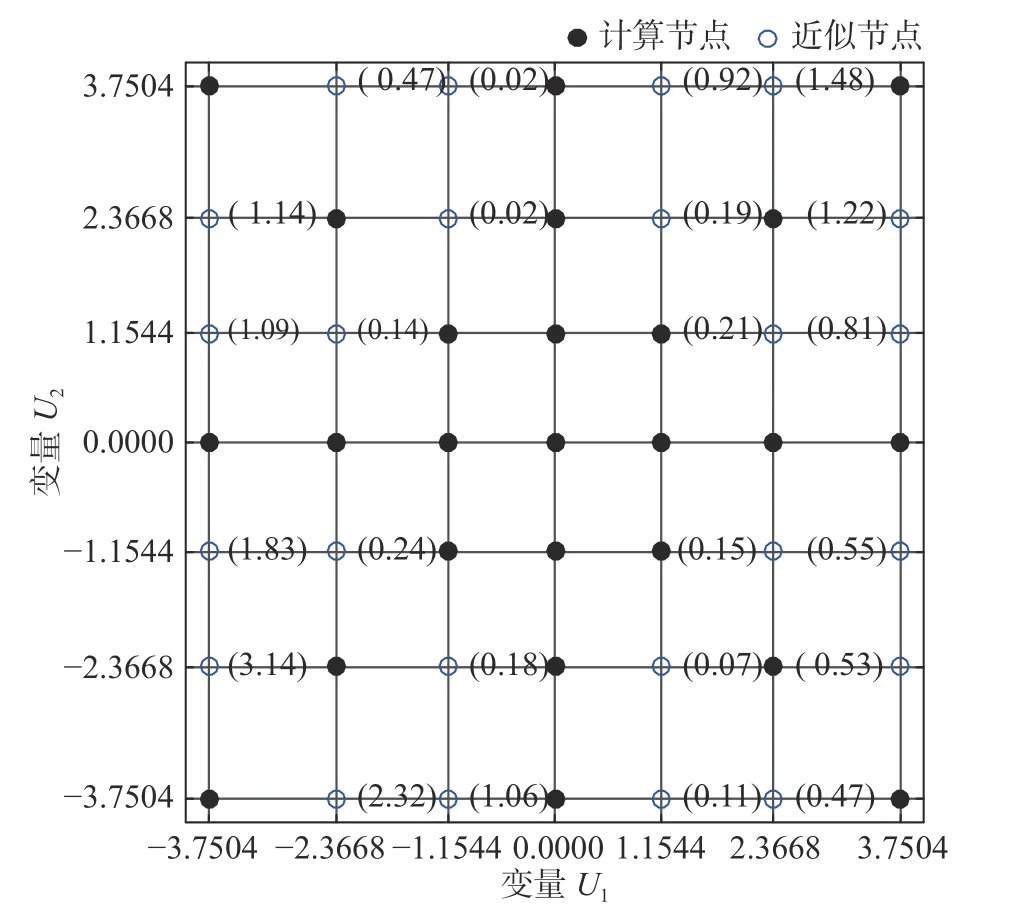
图2 h(U1,U2,12,c)的选点方案和Kriging 近似模型的精度Fig.2 Scheme for selecting points and accuracy of Kriging approximation model of h(U1,U2,12,c)

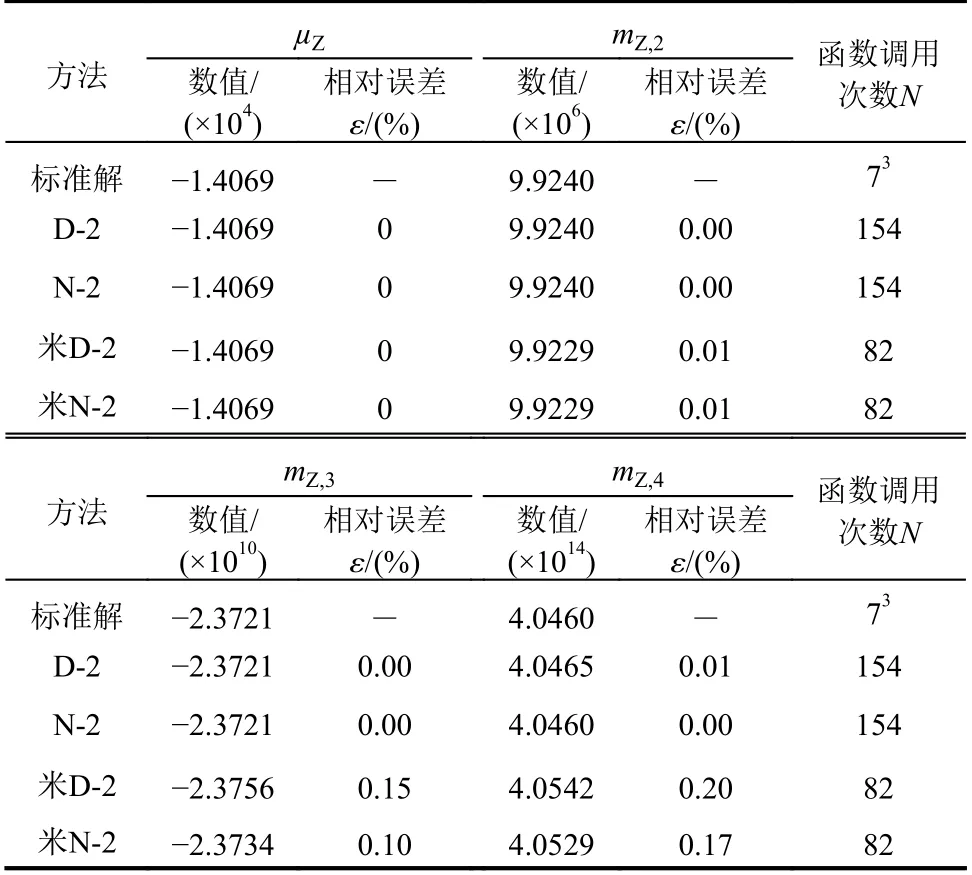
表1 统计矩计算结果对比Table 1 Comparison of statistical moments

算例2.工程算例

考察图3所示承受轴向压缩载荷F的环形截面柱，其功能函数为[22]：

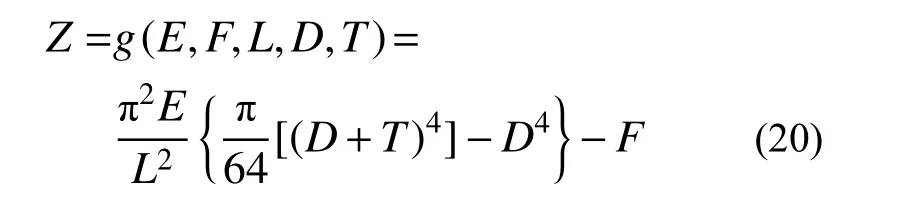
式中：E、F、L、D、T分别是材料弹性模量、轴荷载、柱高、内径和厚度；E、F为对数正态变量，均值为2.1×1011Pa 和6000 N，标准差为0.4×1011Pa和400 N；D、T、L是独立的正态变量，均值分别为0.03、0.006和2.5，标准差分别为0.001、0.0004和0.09。

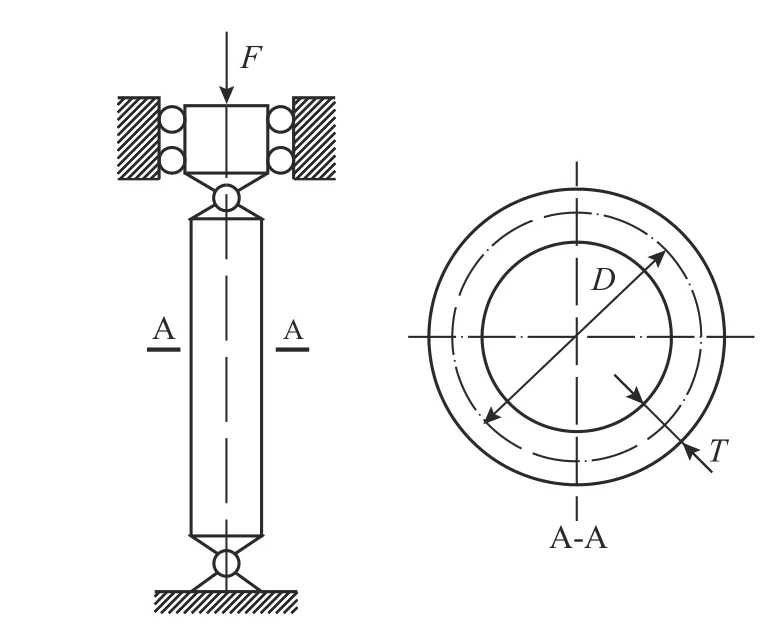
图3 环形柱模型Fig.3 Model of an annular section column

分别采用D-2、N-2和米D-2、米N-2四种方法计算式(20)所示功能函数的前四阶矩，标准解为多维Gauss-Hermite数值积分迭代收敛的结果，结果如表2所示。从表2可以发现：1)高阶矩计算结果中，D-2较N-2精度偏低，米D-2较米N-2精度偏低，米D-2和米N-2分别较D-2、N-2略高，其原因在于建议两方法中降维近似误差和Kriging 近似误差的相互抵消；2)函数调用次数上，D-2和N-2相同，米D-2和米N-2相同，且由于引入了Kriging 近似后两者的计算效率提升1倍多，效果显著。

算例3.工程算例

式中：MUF、UTS、δ、N、R、R0分别是材料利用率、极限拉伸强度、密度、转子转速、外半径和内半径；上述各变量均为独立正态分布变量，其均值分别0.8358、22 000、0.29、21 000、24和8，标准差分别为0.2、5000、0.005、1000、0.5和0.3。

分别采用D-2、N-2和米D-2、米N-2四种方法计算式(21)所示功能函数的前四阶矩，标准解为3×107个样本点的蒙特卡罗法的计算结果，结果如表3所示。从表3可以发现：1)D-2和N-2两者精度相当，米D-2较米N-2略低，且前两者在二、三阶矩精度较后两者略好，但在四阶矩精度略差，因此，建议方法中的降维近似误差和Kriging近似误差的叠加效应和抵消效应对于各阶矩并不总是保持一致；2)建议方法的函数调用次数从现有方法的577次降为217，计算效率显著提高。

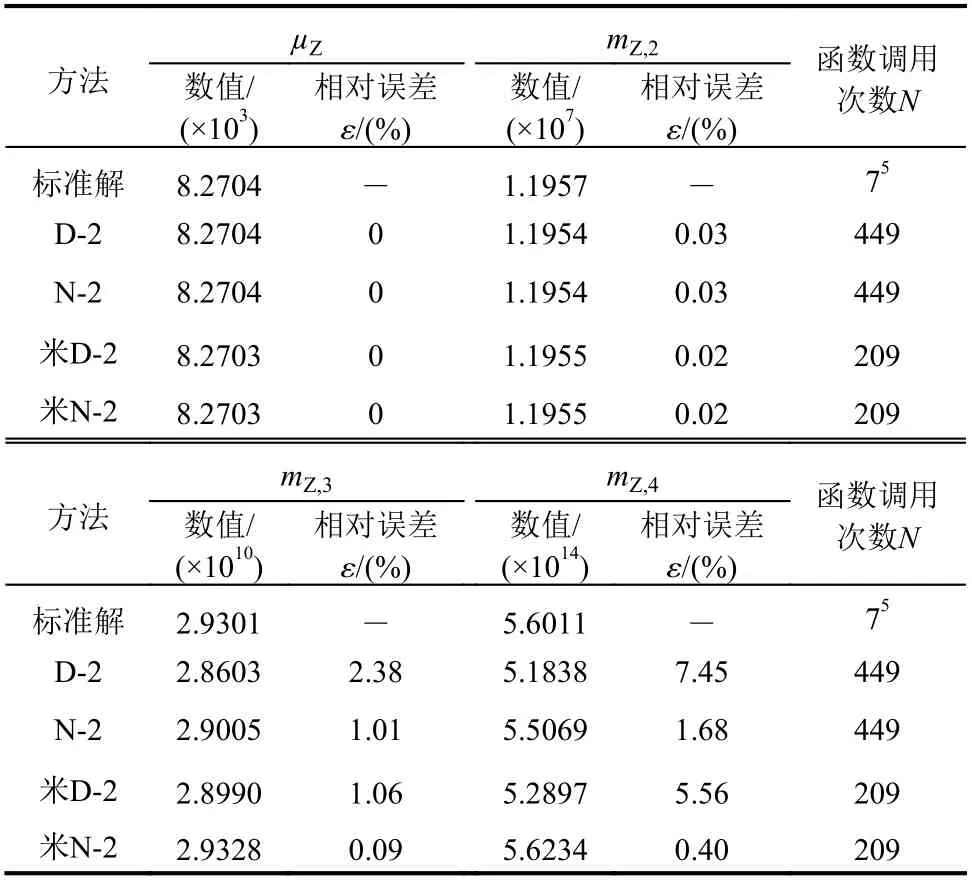
表2 统计矩计算结果对比Table 2 Comparison of statistical moments

表3 统计矩矩计算结果对比Table 3 Comparison of statistical moments

进一步对比上述3个算例，随机系统维数从3上升至6时，现有方法的函数调用次数从154上升至577，而本文建议方法则从82上升至217。事实上，由算例1的效率分析可以发现基于双变量降维近似模型的统计矩估计方法的函数调用次数与参考点坐标有着较大的关系。考察n变量函数，对于参考点坐标均为0和参考点坐标均不为0两种极端情况，N-2(或D-2)与米N-2(或米D-2)的函数调用次数表达式为：

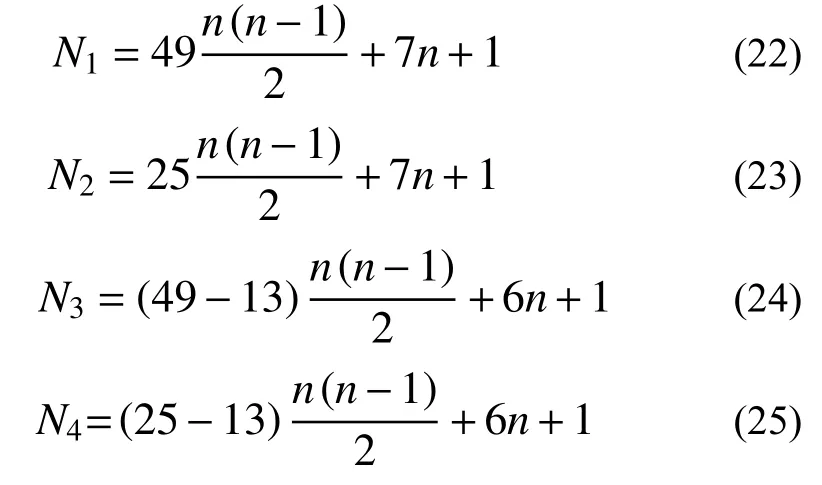
式中：N1、N2分别为参考点坐标均不为0时N-2与米N-2的函数调用次数；N3、N4分别为参考点坐标均为0时N-2与米N-2的函数调用次数。图4给出了2 种情况下各方法函数调用次数随维数的变化规律，虽然米N-2的函数调用次数与N-2具有类似的增长规律，但总的分析次数显著减少。若定义：

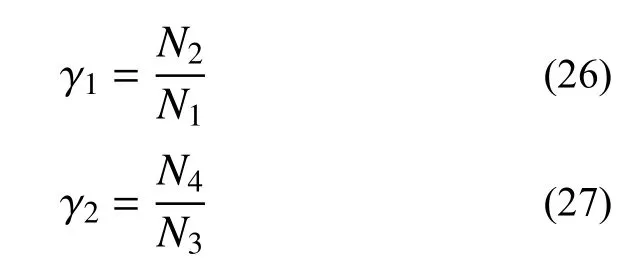
显然，γ1和γ2分别反映了两种极端情况下米N-2 与N-2的函数调用次数的比值。图5给出了γ1和γ2随维数的变化规律，不难发现γ1约为52%，γ2约为35%。

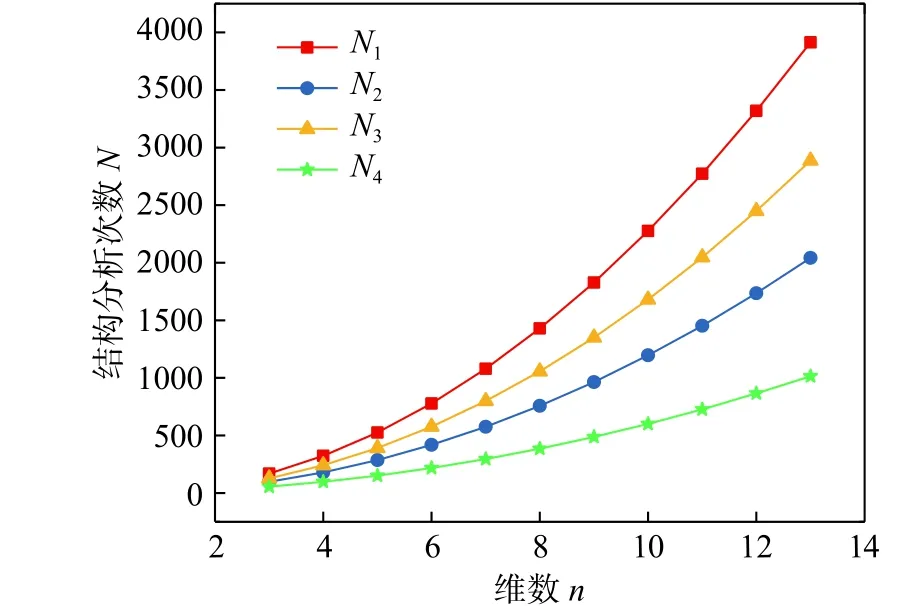
图4 功能函数调用次数对比图Fig.4 Comparison of structural analysis times

易知，对于参考点坐标不全为0的一般情况，米N-2与N-2的函数调用次数的比值应在35%～52%。换言之，相比于已有方法，文中建议方法可提升1倍的计算效率，能更好地兼顾精度和效率。

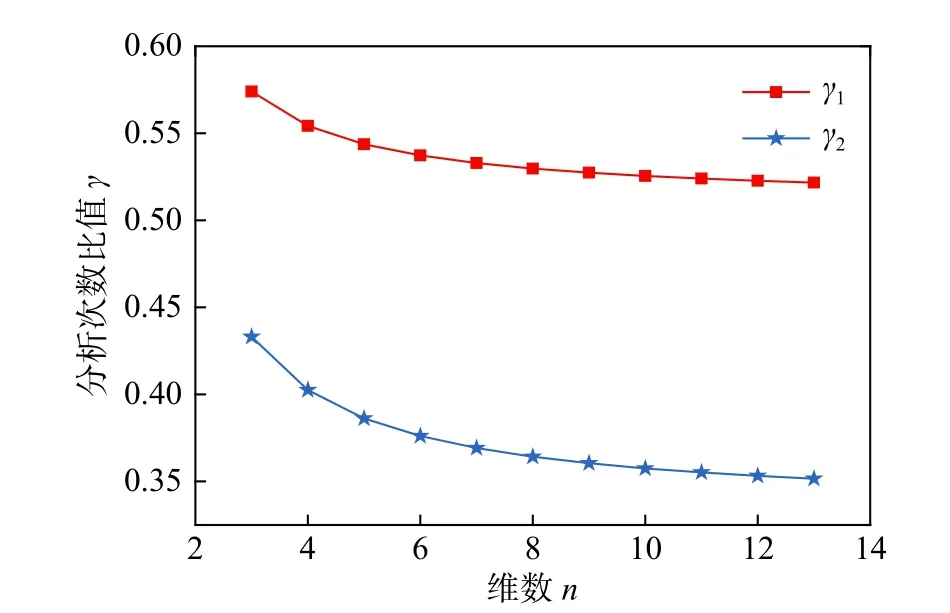
图5 效率相对比值图Fig.5 Comparison of efficiency ratios

4 结论

为了进一步提高基于双变量降维近似模型的统计矩估计方法的效率，本文发展了基于“米”字形选点策略的双变量函数的Kriging 近似模型，并结合现有的矩函数或原函数双变量降维近似模型，提出了更好地兼顾精度和效率的改进统计矩估计方法。文中分析结果表明：

(1)本文建议方法(米N-2和米D-2)的计算效率相比于现有方法(N-2和D-2)显著提高，函数调用次数约为现有方法的50%左右；

(2)建议方法的误差主要包括降维近似误差和Kriging 近似误差，两种误差有时叠加、有时抵消；总体而言，建议方法与现有方法的精度大体相当；

(3)建议的米N-2和米D-2中，米N-2具有相对更好的精度，可优先采用。