单轴对称十字型钢混凝土短柱轴压性能试验研究

周天华，余吉鹏，李亚鹏，张 钰

(长安大学建筑工程学院，西安710061)

工程应用中，根据建筑设计或使用功能的需要，常要求梁表面与柱面平齐，导致梁、柱轴线不重合，从而形成梁柱偏心连接节点[1](图1)。

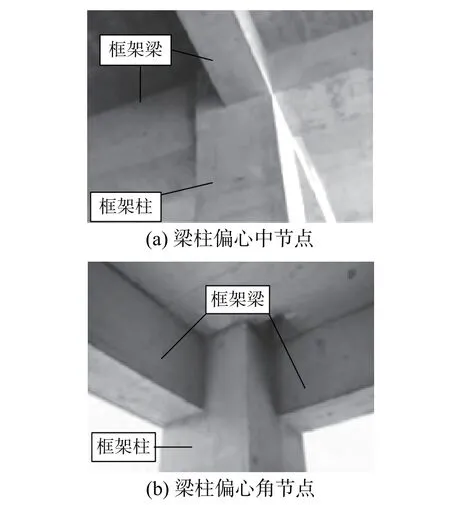
图1 梁柱偏心节点Fig.1 Beam-column eccentric connection

对于型钢混凝土结构，为满足型钢混凝土柱与型钢混凝土梁偏心设置的要求，常将型钢混凝土柱中型钢非对称配置[2−4]，非对称型钢的常见配置形式如图2所示。

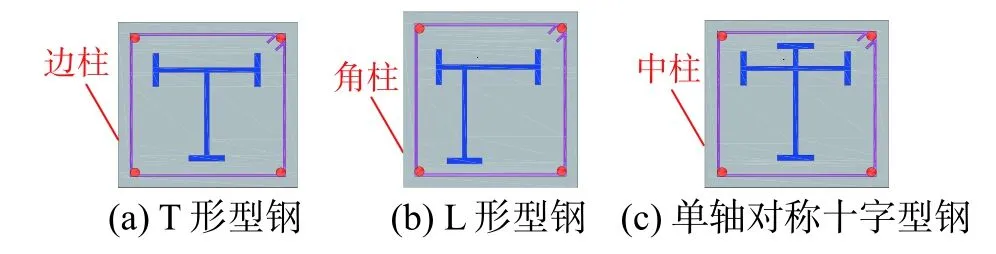
图2 非对称配钢组合柱Fig.2 Composite column with unsymmetrical steel section

国内外对配置对称型钢混凝土柱的轴压[5−6]、偏压[7 − 8]和抗震性能[9− 10]进行了系统研究，形成了较为成熟的设计计算理论和构造措施。而对于配置非对称型钢混凝土柱，王秋维等[11]通过理论分析，建立了配置T 形型钢的组合柱正截面承载力计算方法。曲哲等[12]采用叠加法，提出配置非对称型钢组合柱正截面承载力简化计算方法。曾磊等[13−14]对配置T形和L 形型钢的组合柱抗震性能进行研究，结果表明，滞回曲线出现正负不对称现象。Roik 等[15]根据欧洲规范4，建立了非对称型钢混凝土柱压弯承载力计算方法。Cheng 等[3]对配置T形型钢的组合柱抗震性能进行试验研究，研究表明，T 形配钢对组合柱破坏模式和滞回性能影响较大。Nishimura 等[16]研究了加载方向对配置T 形型钢的组合柱抗震性能的影响，结果表明，加载角度对该组合柱抗弯承载力影响显著。综上可知，型钢非对称配置对组合柱受力性能影响较大，现有关于配置对称型钢混凝土柱的研究成果无法直接应用到配置非对称型钢混凝土柱中；同时现有研究主要集中在配置T形、L 形型钢混凝土边柱和角柱受力性能，对于图2(c)所示的单轴对称十字型钢混凝土中柱受力性能的相关研究尚未见报道，我国规范JGJ 138−2016[17]和YB 9082−2006[18]也无该组合柱相关设计计算内容。

本文设计了9个单轴对称十字型钢混凝土短柱试件，通过轴心受压试验，考察其破坏特征及轴压性能，在分析其受力机理的基础上，根据箍筋和型钢对混凝土约束作用的不同，将组合柱截面混凝土划分不同的约束区，基于Mander 本构模型[19]，提出该组合柱轴压承载力计算方法，为该组合柱的后续研究和工程应用提供参考。

1 试验概况

1.1 试件设计与制作

试验设计了9 个单轴对称十字型钢混凝土短柱试件，截面尺寸为450 mm×300 mm，柱高900 mm，型钢为Q235钢板焊接，箍筋和拉筋为 12的钢筋，纵筋为 16的钢筋，配筋率为2.08%。试件构造及配筋见图3。试件参数为十字型钢偏心率、混凝土强度、含钢率和箍筋配箍率，参数的选取满足《组合结构设计规范》(JGJ 138−2016)[17]中相关规定，同时，含钢率取值范围在5%～8%，型钢和混凝土材料强度组合基本按实际工程常用取值设计[20−21]。试件参数设置见表1。

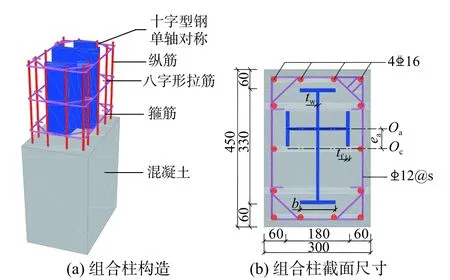
图3 试件截面尺寸及构造Fig.3 Dimensionsand detailsof specimen

表1 试件参数Table 1 Design parameters of specimens

1.2 试件材性

钢材和混凝土力学性能根据标准试验方法测量，实测结果见表2和表3所示。

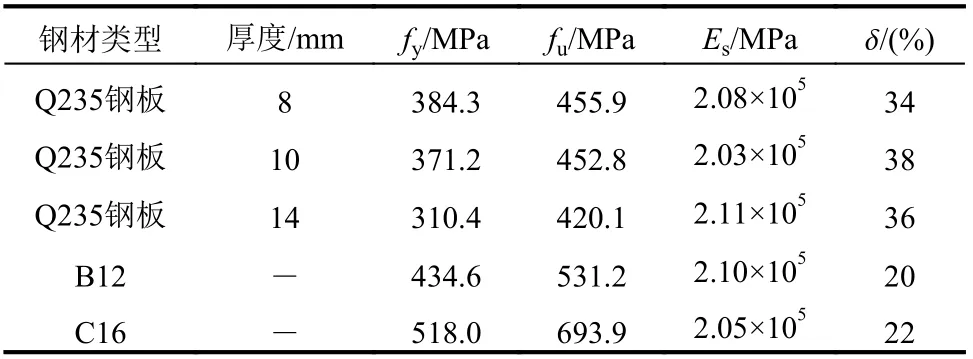
表2 钢板与钢筋材性试验结果Table 2 Material properties of steel plates and steel bars

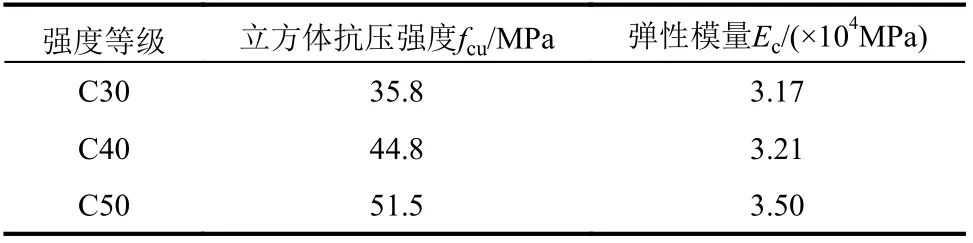
表3 混凝土力学性能Table 3 Mechanical propertiesof concrete

1.3 截面物理形心位置确定

为实现单轴对称十字型钢混凝土柱轴心受力，需要确定不同组合柱试件截面物理形心位置，由于试件中配置的型钢截面非对称，且钢材和混凝土弹性模量和强度均不相同，本文采用文献[15]给出的强度换算截面法计算该组合柱截面物理形心位置。

为便于分析，建立图4所示坐标系，设Oa为纵向H 型钢截面对称轴，Oc为组合柱截面几何形心轴，Om为组合柱截面物理形心轴[18]，定义纵向H 型钢截面对称轴Oa偏离组合柱截面几何形心轴Oc的距离为十字型钢偏心距ea，则十字型钢偏心率为十字型钢偏心距ea与十字型钢偏心方向组合柱截面高度h的比值。(xm,ym)为组合柱截面物理形心om的坐标，由于型钢为单轴对称截面，组合柱截面物理形心到x轴距离均为150 mm，截面物理形心到y轴距离xm按下式计算[15]：

式中：Ac、As和Aa分别为混凝土、钢筋和型钢截面面积；xc、xs和xa分别为混凝土、纵筋和型钢截面形心到y轴的距离；fco为圆柱体抗压强度；fsr和fya分别为钢筋和型钢屈服强度。根据材性试验结果，计算不同试件截面物理形心位置，结果见表1。

图4 组合柱的截面特征Fig.4 Section feature of composite column

1.4 加载装置与制度

试验在陕西省混凝土结构安全与耐久性重点实验室30000 kN压力试验机上进行，试验机加载端底部设置了球铰，顶部为固定端[22]，加载装置见图5。

图5 加载装置Fig.5 Test setup

正式加载前，首先，将加载中心和计算的试件截面物理形心对中；然后，施加预计峰值荷载的20%，进行物理对中，确保试件轴心受力。在试件端部安装夹具，避免试件局部受压破坏。正式加载时，采用位移控制加载，加载速率为0.3 mm/min，当荷载下降到峰值荷载的60%，停止试验[5]。

1.5 测点布置与量测内容

位移计按图6(a)布置，其中，位移计D1、D2量测试件加载端竖向位移值；位移计D3、D4测试试件固定端竖向位移值。

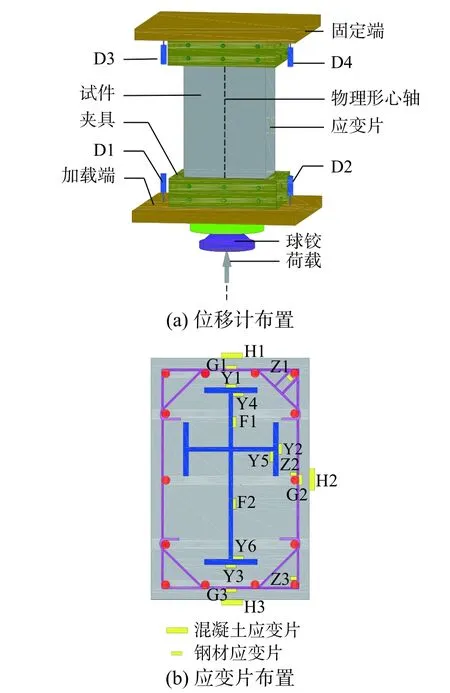
图6 测点布置Fig.6 Measuring pointsarrangement

按图6(b)所示，在试件中间截面布置纵向应变片，以监测试件在加载过程中型钢、纵筋和混凝土应变变化情况；在箍筋和型钢翼缘根部布置横向应变片，以监测混凝土受压膨胀引起的箍筋和翼缘横向变形。

2 试验结果及分析

2.1 试验现象和破坏形态

2.1.1试件SRC-1

试件SRC-1的十字型钢偏心率为0，其破坏现象及特征如下：

1)加载初期，试件处在弹性阶段，试件表面无明显变化。

2)当荷载达到0.4Nm(Nm为峰值荷载)左右时，柱上端出现微裂缝，荷载上升，裂缝发展缓慢。

3)加载至0.8Nm左右时，型钢屈服，箍筋应变发展较快，试件表面出现多条平行于受力方向的微裂缝。

4)荷载增加至0.9Nm左右时，纵筋屈服，试件表面纵向裂缝逐渐贯通，形成多条纵向劈裂裂缝，角部混凝土开始轻微剥落，试件达到峰值荷载(图7(a))。

图7 试件SRC-1破坏形态Fig.7 Failure mode of specimen SRC-1

5)继续加载，混凝土不断剥落，荷载缓慢下降，当荷载下降至峰值荷载的60%，停止试验，试件最终破坏形态见图7(b)。除出试件表面混凝土，发现试件中间截面纵筋被压屈(图7(c))，然后除去型钢外围混凝土，观察到型钢翼缘在混凝土压溃处出现轻微压屈(图7(d))。

试件SRC-1主要破坏特征为试件中间截面混凝土压溃、剥落，纵筋和型钢翼缘在混凝土压溃处发生局部屈曲，试件总体破坏较为均匀。

2.1.2试件SRC-2～SRC-9

试件SRC-2～SRC-9配置的十字型钢存在偏心，上述试件破坏过程及特征较为相似，以SRC-3为例，描述其破坏现象及特征如下：

1)加载初期，试件SRC-3与SRC-1的试验现象无明显区别。

2)加载至0.8Nm附近，试件上端出现多条纵向裂缝，大部分裂缝集中在纵向H型钢偏心方向的远侧，荷载继续增加，纵向裂缝不断向试件底部延伸。

3)当荷载增加到0.9Nm左右时，型钢偏心方向远侧纵向裂缝开始贯通，纵向H 型钢偏心方向裂缝发展缓慢，继续加载，试件纵向H 型钢偏心方向远侧角部混凝土开始剥落，试件达到峰值荷载(图8(a))。

4)继续加载，纵向H 型钢偏心方向远侧混凝土大面积剥落，荷载下降速率较快，当荷载下降到峰值荷载的70%左右，荷载下降速率变慢，试件最终破坏形态见图8(b)。试验结束后，发现型钢偏心方向远侧纵筋明显屈曲(图8(c))，纵向H 型钢偏心方向远侧翼缘在混凝土压碎处出现局部屈曲(图8(d))。

图8 试件SRC-3破坏形态Fig.8 Failure mode of specimen SRC-3

试件SRC-3主要破坏特征为十字型钢偏心方向远侧混凝土破坏严重，混凝土压溃处纵筋和型钢翼缘压屈，试件破坏主要集中在纵向H 型钢偏心方向的远侧。

2.2 荷载-变形曲线

单轴对称十字型钢混凝土柱试件典型荷载-变形(N-Δ)曲线见图9，将其分成以下4个阶段：

1)弹性阶段(OA段)：荷载-变形曲线呈线性发展，型钢和箍筋对混凝土无约束作用。

2)弹塑性阶段(AB段)：荷载上升，型钢和纵筋相继屈服，混凝土不断开裂，横向变形增长速率变大，型钢和箍筋对混凝土约束作用不断增大，曲线斜率逐渐减小，最终试件达到峰值荷载。

3)下降阶段(BC段)：继续加载，纵向H型钢偏心方向远侧混凝土不断剥落，该处纵筋开始压屈，型钢对混凝土的约束作用减弱，荷载下降速率较快。

4)软化阶段(CD段)，当荷载下降到Nr(残余荷载Nr约为峰值荷载的70%)，荷载下降速率变慢，加载后期，荷载主要由型钢及其内部混凝土承担。

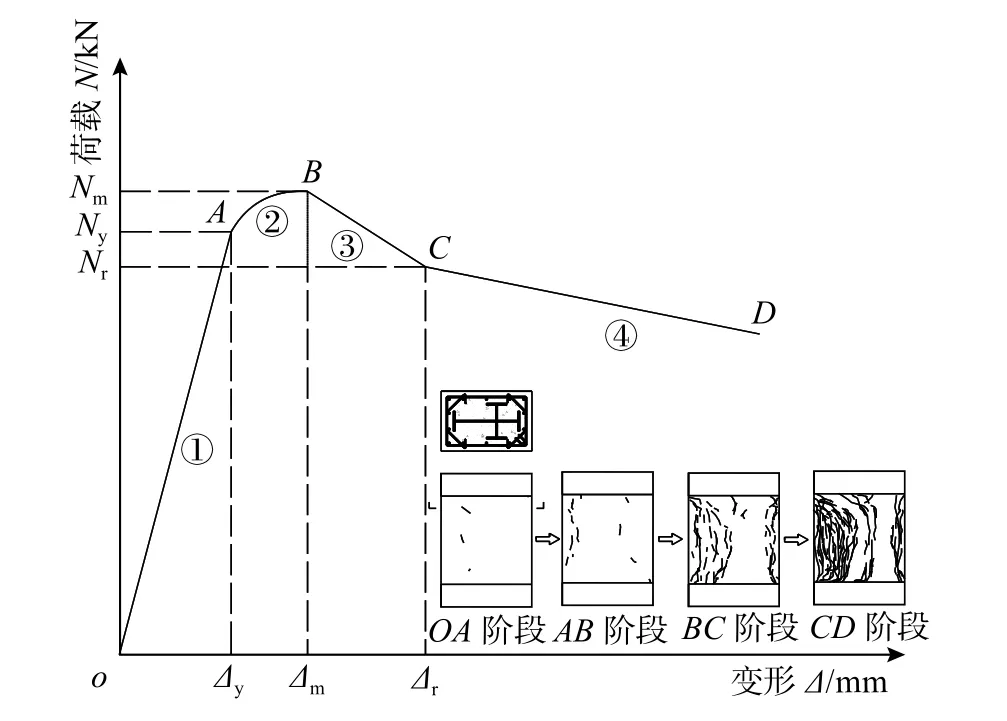
图9 典型荷载-变形(N-Δ)曲线Fig.9 Typical load-deformation curve

2.3 应变分析

试件SRC-2～SRC-9应变变化规律相似，以试件SRC-3为例，与试件SRC-1各部分应变发展规律进行比较。

2.3.1混凝土应变

图10为不同级别轴压荷载作用下，试件中间截面不同位置混凝土应变分布曲线。

由图10可知，加载过程中，试件SRC-1不同位置混凝土应变增长速率基本相同，达到Nm时，不同位置混凝土应变基本相同，约为3200µε。

与试件SRC-1不同的是，试件SRC-3达到0.8Nm后，混凝土(应变片H-3)应变为2095µε，荷载增加，应变基本保持不变；荷载达到Nm时，应变片H-1和H-2应变均达到3300µε左右，出现这种现象的原因是，十字型钢偏心方向远侧混凝土裂缝发展较为迅速，当试件表面混凝土起皮压酥(图8(a))，应变片H-3失效。

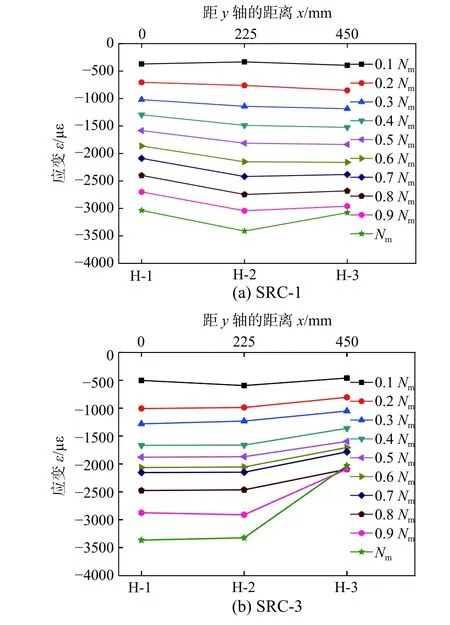
图10 混凝土应变分布曲线Fig.10 Axial strain distribution curvesof concrete

2.3.2型钢和纵筋应变

轴压荷载作用下，不同位置型钢和纵筋应变分布曲线，见图11。

由图11可知，加载前期，试件SRC-1型钢和纵筋应变增长速率基本相同，说明型钢、纵筋和混凝土粘结较好；荷载达到0.8Nm时，型钢翼缘和腹板应变大致相等，约为1900µε，型钢翼缘和腹板均达到屈服；荷载达到0.9Nm时，纵筋应变(应变片Z-1)为2822µε，继续加载，纵筋(应变片Z-3)达到屈服，说明型钢和纵筋的材料性能充分发挥。

对试件SRC-3，当荷载达到0.8Nm，型钢和纵筋应变增长速率加快，但不同位置应变增长速率不同。应变增长速率沿着型钢偏心方向依次递减，随着荷载增加，这种趋势越明显。当荷载达到Nm时，纵筋应变片Z-3为10991µε，远高于纵筋应变片Z-1为2533µε，但纵筋应变片Z-1仍达到屈服。

图11 型钢和纵筋应变分布曲线Fig.11 Axial strain distribution curvesof steel section and longitudinal bar

2.3.3箍筋应变

轴压荷载作用下，不同受力阶段试件箍筋应变分布曲线见图12。

由图可知，加载前期，SRC-1箍筋应变上升缓慢，箍筋基本不产生约束作用；荷载达到0.6Nm，箍筋应变增长速率加快，且长边方向应变(应变片G-2)增长速率高于短边方向(应变片G-1和G-3)应变，长边方向应变(应变片G-2)先达到屈服；荷载达到Nm时，短边方向箍筋应变(应变片G-1和G-3)大致相等，约为2400µε，均达到屈服应变。

与试件SRC-1不同的是，试件SRC-3荷载达到0.9Nm时，型钢偏心方向远侧箍筋(G-3)应变为1184µε，型钢偏心方向近侧箍筋应变(应变片G-1)为657µε，箍筋应变(应变片G-3)增长速率高于应变(应变片G-1)，原因是纵向H 型钢偏心方向型钢对混凝土的约束作用较强，混凝土横向变形相对较小。

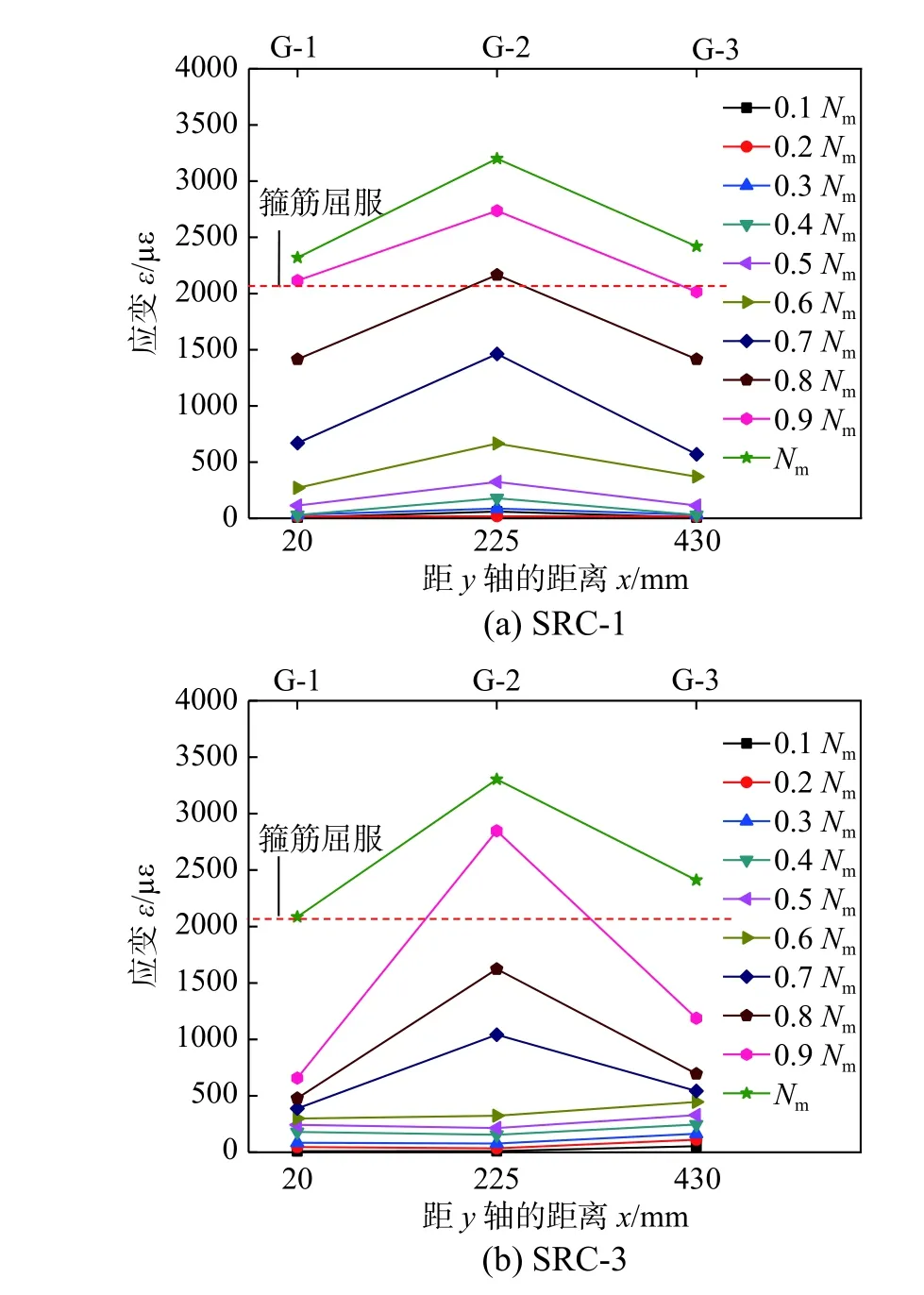
图12 箍筋应变分布曲线Fig.12 Strain distribution curvesof stirrup

2.4 试件受力机理分析

综合上述试验现象和应变变化规律，对该组合柱轴压受力机理进行分析。

轴压荷载作用下，由于泊松效应，箍筋和型钢对混凝土产生约束力，根据Mander 本构模型[19]，约束应力以拱的形式作用在混凝土上，根据箍筋和型钢约束作用的不同，将组合柱截面分成箍筋非有效约束区、箍筋有效约束区和复合约束区，见图13。其中，箍筋有效约束区仅受箍筋约束作用，复合约束区受箍筋和型钢的双重约束作用。

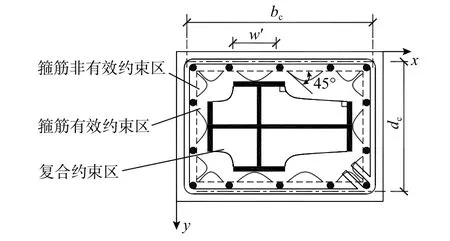
图13 截面约束示意图Fig.13 Confined concrete of cross section

加载初期，试件处于弹性阶段，型钢和箍筋对混凝土无约束作用；荷载增加，混凝土裂缝不断发展，型钢进入弹塑性阶段，混凝土泊松比νc超过型钢泊松比νs，型钢和箍筋逐渐对混凝土产生约束力。

为研究单轴对称十字型钢对其内部混凝土的约束作用，取单轴对称十字型钢混凝土芯柱1/4截面进行分析，见图14。

图14 型钢混凝土芯柱截面示意图Fig.14 Cross section of composite core column

其中，A1区域混凝土受型钢的侧向约束应力实际分布情况[5,23]见图15(a)，约束应力主要分布在翼缘和腹板、腹板和腹板相交处。为简化分析，参考文献[23 −24]提出的型钢约束应力简化分布形式，将分布在AG和ED边较小的约束应力忽略，同时将型钢侧向约束应力简化为均匀分布，见图15(b)。

图15 侧向约束应力分布Fig.15 Distribution of lateral confining stress

根据图15(b)型钢约束混凝土的简化约束状态，将型钢混凝土芯柱截面划分成型钢强约束混凝土、型钢弱约束混凝土和型钢无约束混凝土[23]，见图16。其中，型钢强约束混凝土(I区)受型钢x、y向双向约束应力，型钢弱约束混凝土(II区、III区和IV 区)仅受型钢x或y向单向约束应力，型钢无约束区(V 区)不受型钢的约束作用。

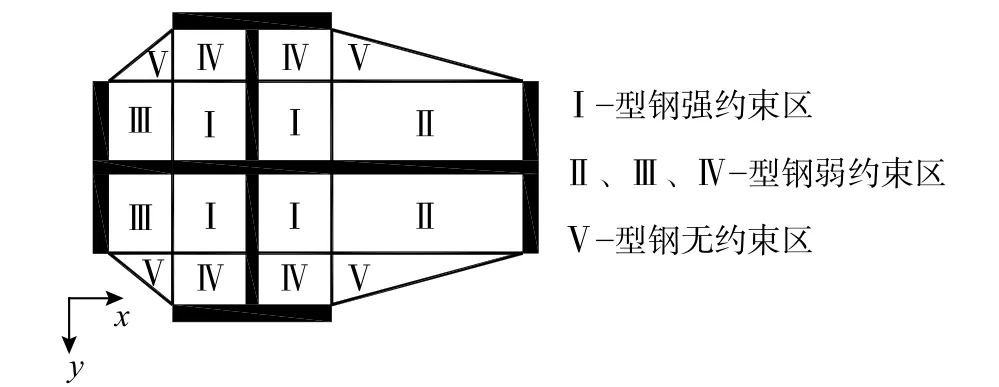
图16 单轴对称十字型钢混凝土芯柱截面区域划分Fig.16 Region for SRCcore column with monosymmetric cross-shaped steel

荷载增加，混凝土横向变形增大，但由于型钢约束应力分布不均匀，型钢弱约束混凝土(II区)受到的约束作用相对较弱，该区混凝土横向变形增长较快，纵向H 型钢偏心方向远侧混凝土裂缝发展较为迅速(图8(a))；当荷载达到0.8Nm，型钢和箍筋开始屈服，型钢偏心方向远侧混凝土损伤加剧，该方向型钢翼缘和纵筋应变增长速率加快，试件截面受力不均匀，应力重分布，损伤向纵向H型钢偏心方向发展；当型钢翼缘根部由于混凝土膨胀变形受拉屈服，试件达到Nm；此后，虽然型钢开始发生强化，但由于混凝土强度退化速度较快，纵筋开始压屈，荷载逐渐下降。

3 参数分析

表4 给出了试件荷载-变形曲线各特征点荷载N、位移Δ和延性系数µ。表中屈服点采用等量法确定，屈服点位移为Δy，取荷载下降到峰值荷载Nm的85%作为试件的破坏点，相应位移为极限位移Δu，位移延性系数µ为[25]：

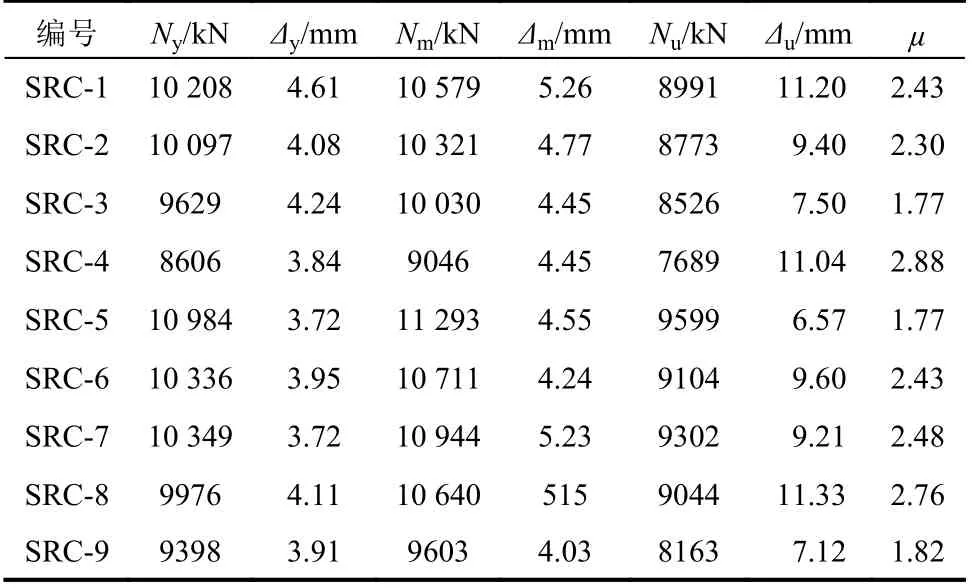
表4 试件特征荷载及位移Table 4 Loadsand displacementsof characteristic points

3.1 十字型钢偏心率的影响

不同十字型钢偏心率试件荷载-变形曲线比较见图17。

由图17和表4可知，增加十字型钢偏心率，对试件初始轴向刚度影响较小，对其峰值后变形能力影响较大，试件SRC-1、SRC-2和SRC-3十字型钢偏心率分别为0、0.11和0.22，试件SRC-3相比于SRC-1轴压承载力下降了5.18%，延性系数下降了27.16%，可见，十字型钢偏心率增大对试件轴压承载力和延性产生不利影响，由于纵向H 型钢偏心，导致型钢约束应力分布不均匀，达到Nm后，纵向H 型钢偏心方向远侧混凝土先压溃，截面受力不均匀，荷载迅速下降，变形能力显著降低。

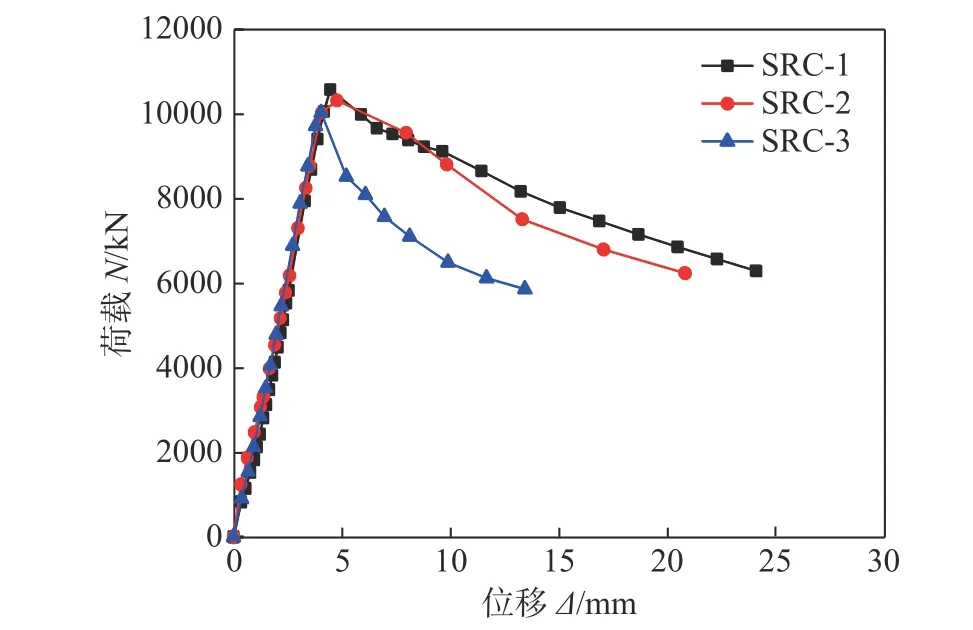
图17 十字型钢偏心率对试件荷载-变形曲线影响Fig.17 Load-deformation curvesof specimens with different cross-shaped steel eccentricity ratio

3.2 混凝土强度的影响

不同混凝土强度试件荷载-变形曲线比较见图18。

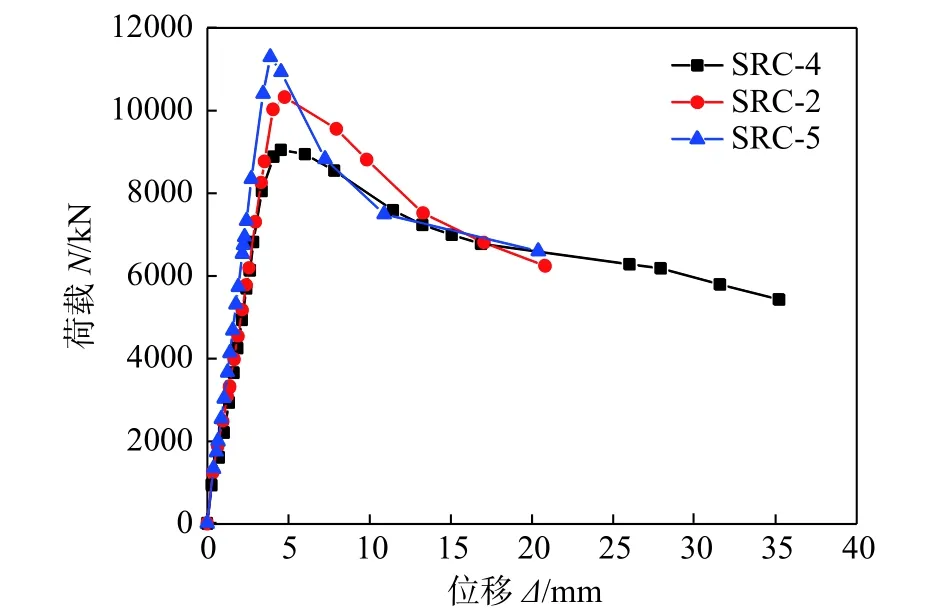
图18 混凝土强度对试件荷载-变形曲线影响Fig.18 Load-deformation curves of specimens with different concrete strength

由图18和表4可知，混凝土强度从35.8 MPa增加到51.5 MPa，试件初始轴向刚度略有提高，轴压承载力提高了24.83%，延性系数下降了38.54%，说明混凝土强度对组合柱轴压性能影响显著，因为混凝土强度越高，脆性越明显，泊松效应越不显著，试件破坏越突然，后期变形能力越差[26]。

3.3 含钢率的影响

不同含钢率试件荷载-变形曲线比较见图19。

由图19和表4可知，相对于试件SRC-2，试件SRC-6和SRC-7的含钢率分别增加了1.19%和1.86%，试件轴压承载力分别提高了3.77%和6.03%，延性系数分别上升了5.65%和7.83%。说明组合柱含钢率越高，轴压承载力越高，变形能力越好。原因是，钢材自身强度高，塑性变形能力好，增加钢材用量，提高了塑性材料在组合柱中的比例；增加翼缘厚度，增强其对混凝土的约束作用，改善混凝土的强度和变形能力。

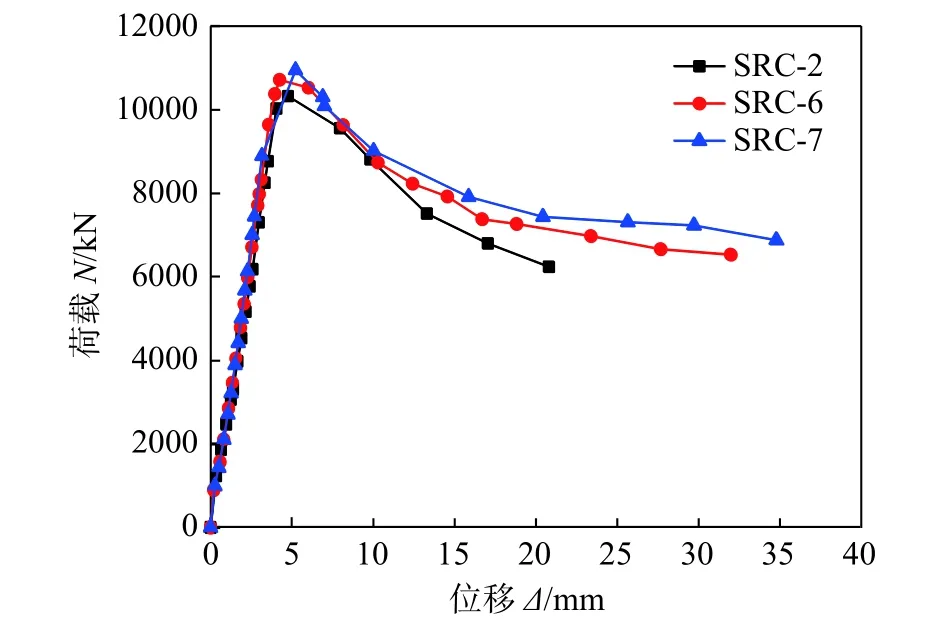
图19 含钢率对试件荷载-变形曲线影响Fig.19 Load-deformation curves of specimens with different steel ratio

3.4 配箍率的影响

不同配箍率试件荷载-变形曲线比较见图20。

由图20可知，配箍率下降，对试件初始轴向刚度影响不大，相比于试件SRC-8，试件SRC-2和SRC-9的轴压承载力分别下降了3.0%和9.74%，延性系数分别下降了16.67%和34.06%。可见，配箍率对组合柱轴压性能影响显著，配箍率提高，箍筋对混凝土的约束作用增强，混凝土强度和变形能力提高。

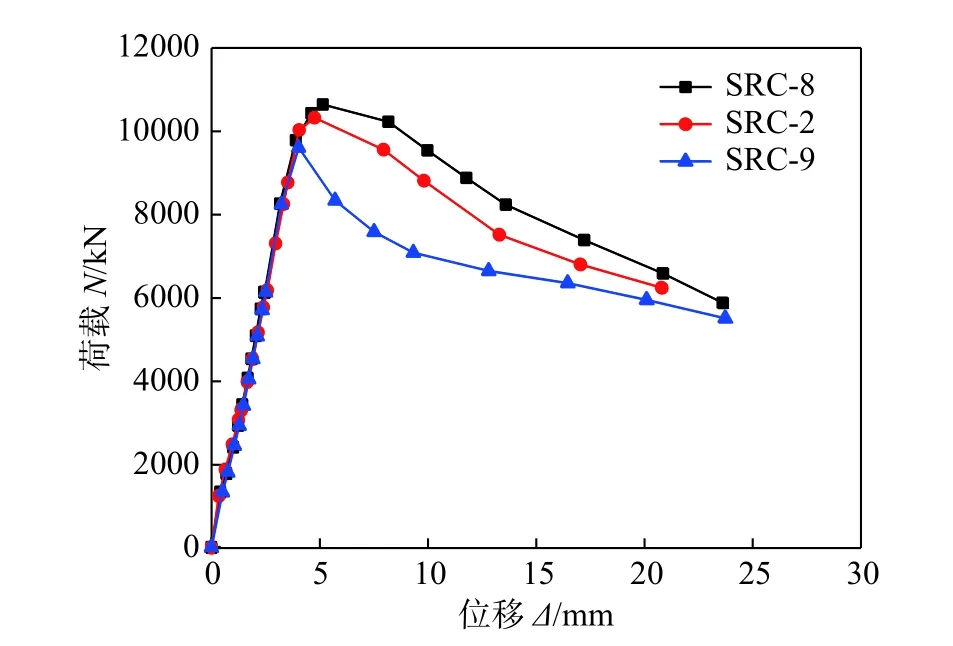
图20 配箍率对试件荷载-变形曲线影响Fig.20 Load-deformation curves of specimens with different volume-stirrup ratio

4 轴压承载力计算

由试验结果可知，试件在受力过程中型钢和混凝土粘结较好，故可将组合柱各部分承担的轴力叠加[5,25]，得到该组合柱轴压承载力。

根据图13对组合柱截面混凝土约束区的划分，将该组合柱轴压承载力Nc分成5部分：箍筋非有效约束区混凝土承担的轴力N1；箍筋有效约束区混凝土承担的轴力N2；复合约束区混凝土承担的轴力N3；纵筋承担的轴力Ns；型钢承担的轴力Na。则组合柱轴压承载力为：

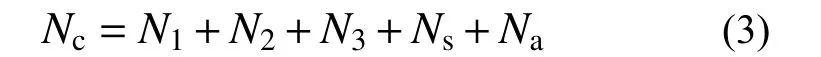
4.1 N1计算

箍筋非有效约束区混凝土提供的承载力为：

式中，A1为非有效约束区混凝土面积。

4.2 N2 计算

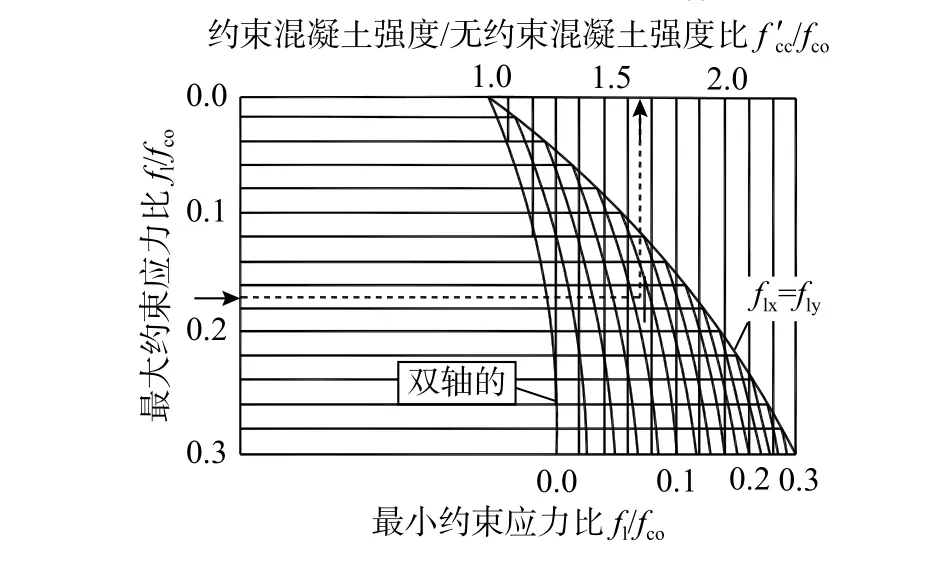
图21 矩形截面约束混凝土强度计算Fig.21 Strength calculation for confined concrete with rectangular cross section

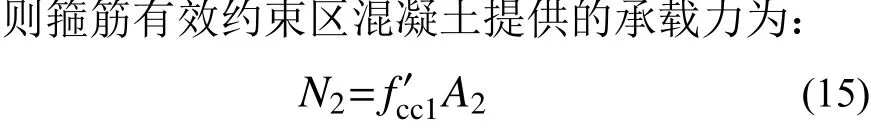
式中，A2为箍筋有效约束区混凝土面积。

4.3 N3计算

文献[24,27]讨论了型钢混凝土柱的约束机理，认为复合约束区混凝土所受的约束作用是箍筋和型钢约束作用的线性叠加。

在计算型钢有效侧向约束应力时，根据图15(b)，将型钢侧向约束应力简化为均匀分布，同时将翼缘外伸段看成悬臂梁，达到峰值荷载时，认为翼缘根部屈服[23−24]，翼缘根部截面内力抵抗弯矩与外力矩相平衡，见图22。

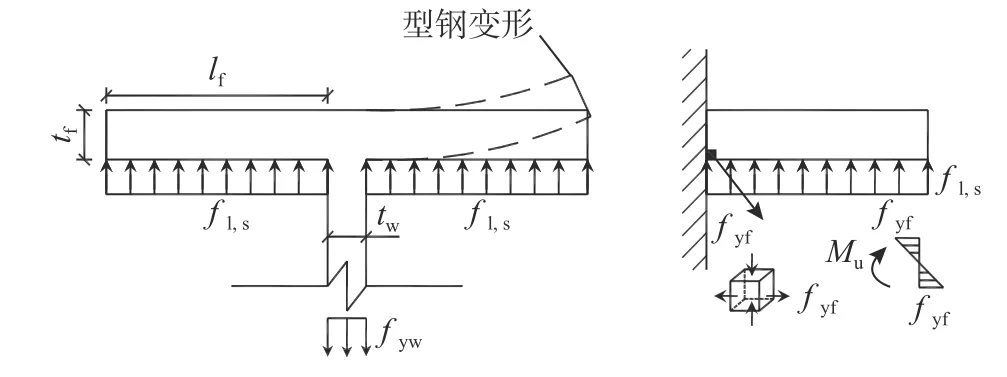
图22 翼缘应力状态Fig.22 Stress state of the flange

式中：fle,sx1和fle,sy1分别为型钢强约束混凝土(I区)受到x和y向的型钢有效侧向约束应力；flhx1和flhy1分别为型钢强约束混凝土(I 区)在x和y向受到的复合有效侧向约束应力。由式(21)和式(22)计算出flhx1和flhy1，查图21[19]可得复合约束区(I区)约束混凝土强度fc′c2。

同理，根据型钢弱约束混凝土(II 区、III区和IV 区)不同的约束状态，将箍筋和型钢x和y方向不同有效侧向约束应力叠加，得到不同复合约束混凝土强度，根据式(5)～式(10)，得到各约束区混凝土本构关系，见图23。

则复合约束区混凝土承担的轴力为：

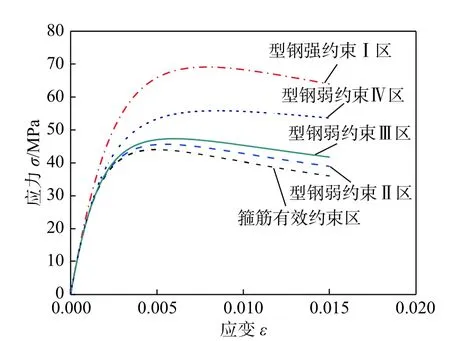
图23 不同约束区混凝土本构关系Fig.23 Constitutive relationsof concrete indifferent confined areas

4.4 N s计算

纵筋提供的承载力为：

4.5 N a 计算

型钢提供的承载力为：

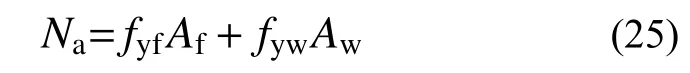
式中：fyw为腹板屈服强度；Af和Aw分别为翼缘和腹板的截面面积。

综上，将上述5部分承载力叠加，得到该组合柱轴压承载力计算公式为：

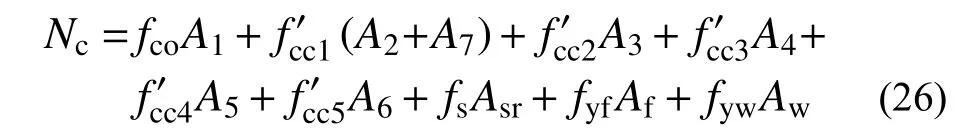
4.6 计算式退化

当十字型钢对称配置时，根据图15(b)型钢约束混凝土简化约束状态，十字型钢混凝土柱截面约束区划分见图24。其中，型钢无约束区不受型钢的约束作用，仅受箍筋的约束作用，故将型钢无约束区与箍筋有效约束区合并。

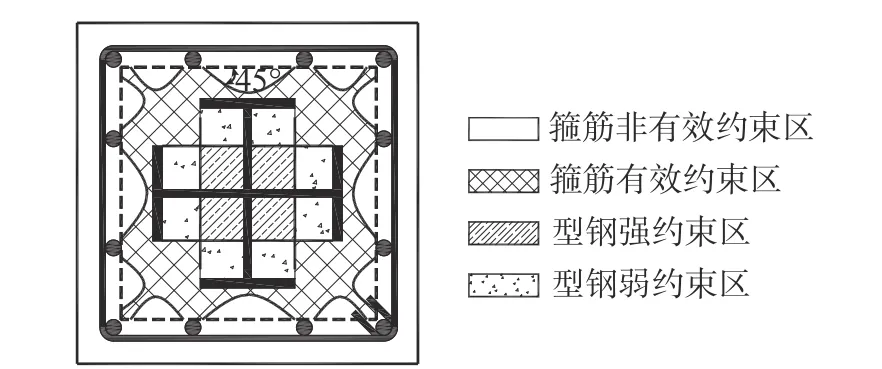
图24 十字型钢混凝土柱截面划分Fig.24 Region for SRCcolumn with cross-shaped steel

由于该组合柱十字型钢对称配置，型钢弱约束区(II区、III区和IV 区)混凝土强度相等，则该组合柱轴压承载力计算公式可由式(26)退化为：

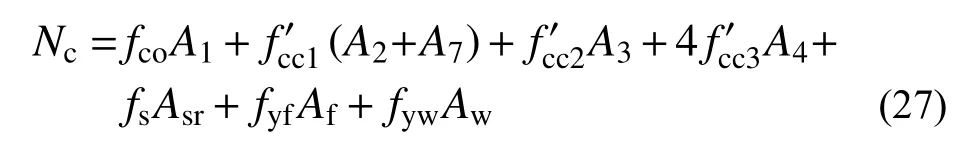
5 试验结果验证

5.1 各国规范验证

目前，中国JGJ 138−2016规范[17]、欧洲EC4规范[28]和美国ACI318−14规范[29]给出了型钢混凝土柱轴压承载力计算公式，但均未涉及单轴对称十字型钢混凝土柱。现结合本文研究，验证上述规范是否能够直接用于单轴对称十字型钢混凝土柱。

采用上述规范计算时，材料强度采用实测值，计算结果见表5。

由表5可知，试验值与中国JGJ 138−2016规范、欧洲EC4规范和美国ACI 318−14规范计算值的比值均值分别为1.41、1.26 和1.49，变异系数分别为0.035、0.035和0.034，说明上述规范计算结果均偏于保守，且无法考虑十字型钢偏心对该组合柱轴压承载力的影响，原因是上述规范未考虑箍筋和型钢对混凝土的约束作用。

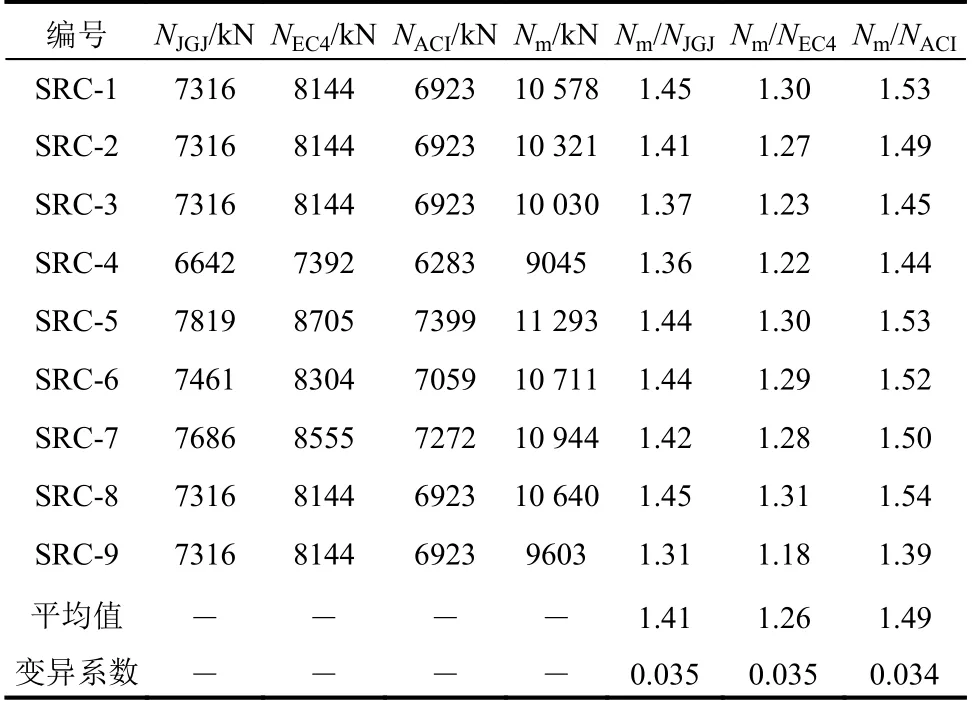
表5 试验结果与规范计算结果比较Table 5 Comparison between experimental resultsand computed resultscalculated by the standards

5.2 本文公式验证

采用式(26)计算本文试件轴压承载力，计算结果见表6。由表可知，试验值与计算值比值均值为1.05，变异系数为0.025，说明试验值与计算值吻合较好，提出的轴压承载力计算公式能较为准确预测该组合柱轴压受力性能。

采用退化式(27)对文献[30]中十字型钢混凝土柱轴压承载力进行计算，结果见表7。由表可知，试验值与计算值吻合较好，说明式(27)适用于对称十字型钢混凝土柱。

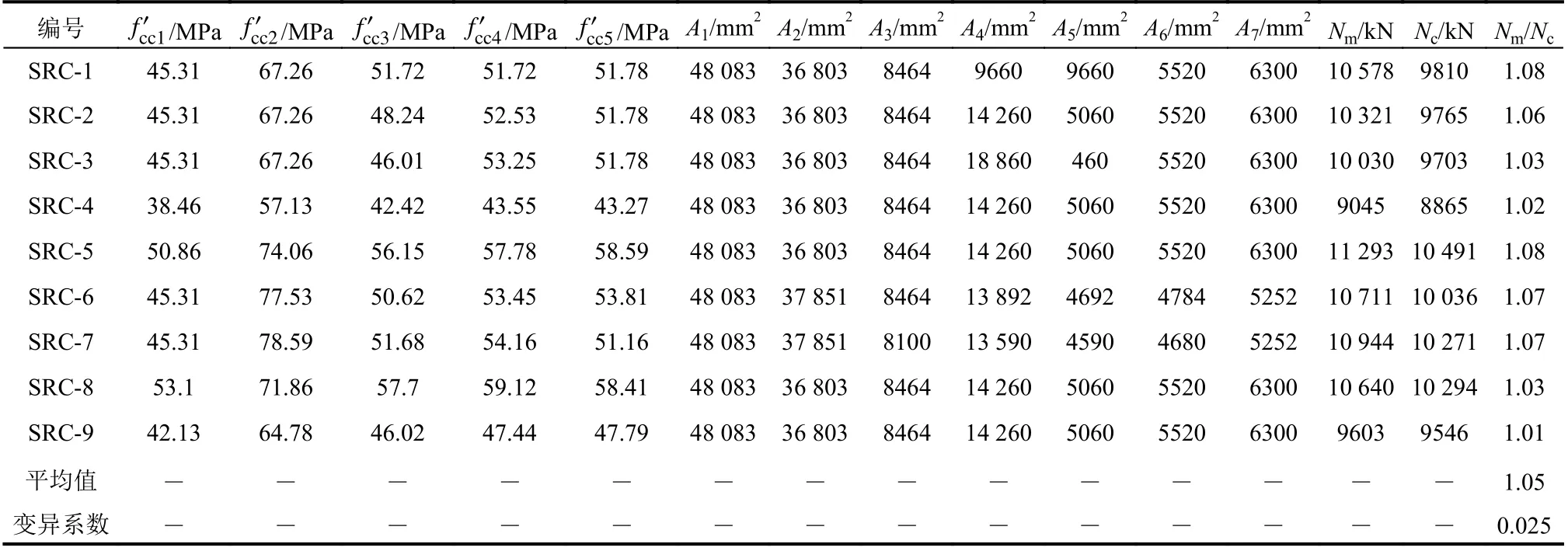
表6 试验结果与计算结果Table 6 Comparison between experimental results and calculation results

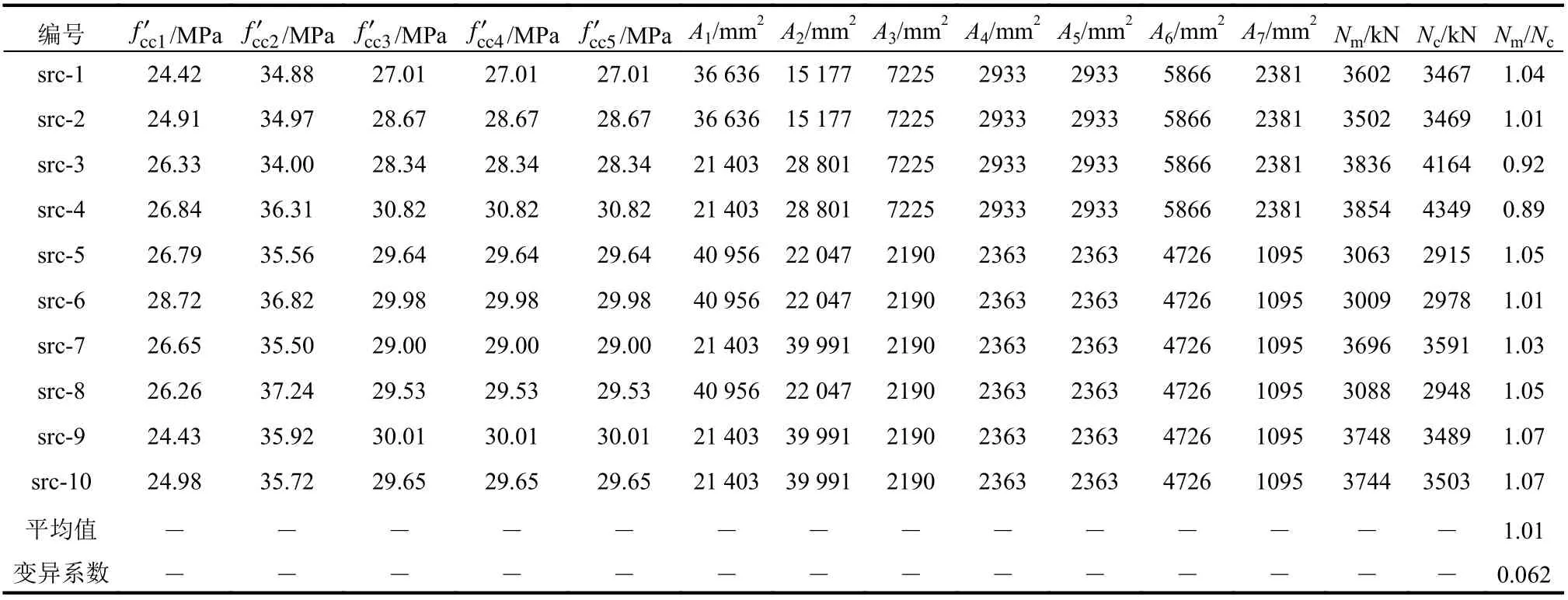
表7 文献[30]试验结果与计算结果比较Table 7 Comparison between experimental resultsfor specimensin literature [30]and calculation results

6 结论

本文对单轴对称十字型钢混凝土短柱进行了轴心受压试验，研究了该组合柱轴压受力机理，基于Mander 本构模型，建立了该组合柱轴压承载力计算方法，得出以下结论：

(1)单轴对称十字型钢混凝土柱试件破坏集中在纵向H型钢偏心方向远侧。荷载-位移曲线可分成弹性段、弹塑性段、下降段和软化段。达到峰值荷载时，柱截面应变分布不均匀，纵向H 型钢偏心方向远侧型钢应变较大。

(2)十字型钢偏心率由0增至0.22，试件轴压承载力下降了5.18%，延性下降了27.16%；混凝土强度由35.8 MPa 提升到51.5 MPa，试件轴压承载力上升了24.83%，延性下降了38.54%；含钢率从5.70%增长到7.56%，试件轴压承载力提升了6.03%，延性上升了7.83%；箍筋间距从100 mm增加到200 mm，试件轴压承载力降低了9.74%，延性系数下降了34.06%。

(3)将组合柱轴压承载力分成5部分，基于Mander 本构模型，根据叠加原理，建立了单轴对称十字型钢混凝土短柱轴压承载力计算方法。采用规范对该组合柱轴压承载力进行验算，规范计算结果均偏于保守，本文提出的轴压承载力计算公式计算结果与试验值吻合较好，且该公式可推广到对称十字型钢混凝土柱。