高精度空气折射率测量系统设计与实现
闵帅博,严利平,崔建军,王 冬,束红林,陈 恺
(1.浙江理工大学纳米测量技术实验室,浙江杭州310018; 2.中国计量科学研究院,北京100029; 3.天津大学精密仪器与光电子工程学院,天津300072; 4.河南理工大学机械与动力工程学院,河南焦作454000)
1 引 言
激光干涉仪在几何量计量中有着广泛的应用,该方法以非接触、高精度、大量程等优点,尤其在微位移测量领域[1,2]和高精密位移传感器的标定工作[3]中更为突出。限制激光干涉仪测量精度的一个关键因素是空气折射率。在激光干涉仪测量微位移时,通常使用激光真空波长代替实际波长进行位移量解算。而在实际测量中,空气折射率的变化会影响传播的激光实际波长,从而降低微位移实测值的准确度。因此许多研究人员对如何准确测量空气折射率进行了大量的研究。
国内外对于空气折射率测量的相关研究方案分为两大类:基于真空环境的直接测量方案和基于经验模型的间接测量方案。
第一种方案是使用激光干涉测量装置获得同一待测量在真空环境和大气环境下的测量值并进行比较,从而解算出空气折射率,这种方案常用于量值溯源研究工作以及精密科学实验中。李东光等[4]基于这种方案提出一种预抽气真空腔测量方法,避免了抽气操作给测量带来的额外误差,补偿后的测量精度可达到10-7;陈强华等[5]设计了一种基于表面等离子体共振和相位检测的测量方法,测量精度优于5×10-6,可以为更高精度的空气折射率测量仪提供足够精确的初值[5]。Yan L P等[6,7]和Chen B Y等[8]提出了一种激光合成波长干涉波动测量方法,将空气折射率的波动转化为参考光路补偿位移的测量,采用殷刚材料作为折射率传感腔时,测量精度可达1.6×10-8,进一步提高了直接测量方案的实际精度。第一种方案在理上论精度可达到10-9,但是由于装置复杂,光路调整要求较高等问题,很难应用到激光干涉仪的环境补偿工作中。
第二种间接测量方案是通过采集周围环境中的温湿度,大气压强等参数,使用实验数据和理论建模相结合得到的模型公式进行间接解算。其研究工作主要是对经典Edlén公式的不断修正。Birch K P等[9]针对空气密度和水蒸气折射率数值的更新、温标的两次改值等变化,对Edlén公式进行改进后的测量不确定度可达到3×10-8。Bönsch G等[10]人分别对4个波长的空气折射率测量实验结果进行数值拟合,对Edlén公式作出进一步的改进,测量结果的标准偏差保持在3×10-9之内。陈强华等[11]提出了相移干涉折射率测量方法,在较高温度14.6~24.0 ℃范围内对633 nm波长下空气折射率的修正系数进行测量,得到其修正公式。在特定条件下,其精度理论上高于最新的Bönsch公式。目前基于间接测量方案的测量装置实际精度并不理想。一方面,现有测量装置传感器自身精度偏低,限制了获取到的原始数据精度;另一方面,大多数测量装置并没有采用最新的解算公式,在解算过程中也会引入一定的误差。而在实际的工程测量过程中,如果折射率测量系统兼顾高精度和易操作两方面[12],则能为激光干涉仪提供更好的补偿效果。
针对用于环境补偿的空气折射率测量系统的高精度和易操作需求,采用高精度环境参数采集装置,并行采集反映环境状态的物理量感知数据。在分析该测量系统工作特性的基础上,设计了用于空气折射率解算的测量分析软件,并对3种常用的间接测量解算公式和相关的精度分析功能进行合理的实现。通过和常用环境补偿器的测量结果进行对比,验证该折射率测量系统整体的高精度和稳定性。
2 空气折射率测量原理
空气折射率间接测量法或称作PTF法。这种方法包括3个解算公式,综合考虑了温度、湿度、压强的影响,进而解算出实际的空气折射率。
该方法的第1个解算公式是用于计算特定波长的激光在标准大气环境下(温度为20 ℃,大气压强为1×105Pa)的标准空气折射率ns,可由标准状态下空气的色散公式变换[13]得到:
(1)
式中:A,B,C为通用系数;σ为激光的真空波数,即激光在真空中波长的倒数,单位为μm-1。
第2个解算公式是在标准空气折射率的基础上,考虑实际温度和压强的影响得出干燥空气折射率npt,具体公式为
(2)
式中:D,E,F,G为通用系数;p为大气压强,单位为Pa;t为空气温度,单位为℃。
第3个解算公式是在实际干燥空气折射率的基础上,考虑空气湿度的影响得出空气折射率nptf
nptf=npt-pf[M-Nσ2]10-10
(3)
式中:M,N为通用系数;pf为水蒸气分压力,单位为Pa。
在实际应用中,水蒸气分压力pf是通过测量空气中的相对湿度来间接计算出来的。相对湿度表示空气中水蒸气分压力与相同温度下的饱和水汽压之比。水蒸气分压力的计算公式为
pf=pf0R
(4)
式中:R为相对湿度;pf0为饱和蒸汽压力。
许多相关学者对饱和蒸汽压进行了实验研究,得出了多种用于计算的经验公式,其中最常用的是Goff-Gratch公式[14]:

(5)
式中:a1=10.795 74;a2=-5.028 00;a3=1.504 751 0-4;a4=4.287 301 0-4;a5=0.786 14;b=-8.296 90;c=4.769 55;T1=273.16 K(水三相点温度);T=273.15+t,T为热力学温度。
在实际应用中,空气折射率测量值的变化主要体现在其尾数上。在后文对于间接测量公式解算结果的分析主要是对折射率值的尾数的分析。
nman=nmea-nrou
(6)
式中:nman为空气折射率的尾数;nmea为空气折射率测量值;nrou为空气折射率的整数部分,取值为1。
目前使用PTF法进行折射率测量时,常用的模型公式有Edlén公式及对其改进后的Birch公式、Bönsch公式。3种公式区别在于通用系数的不同,如表1所示。

表1 3种公式的通用系数Tab.1 General coefficient of three formulas
3种公式是通过在不同的实验环境下测得的数据进行拟合出来的,其应用的实验环境也会有差异。其中,Edlén公式和Birch公式应用在波长为633 nm附近的激光测量工作中,而Bönsch公式应用在波长为644.0 nm、508.7 nm、480.1 nm和467.9 nm附近的激光测量工作中。表2是3种公式的具体应用环境要求。

表2 3种公式的应用环境Tab.2 Application environment of three formulas
从表2中可以看出,3种公式都能够满足大多数实验室环境的要求,压强变化可在98~100 kPa范围内,温度变化可在20~25 ℃范围内,湿度变化可在(35~45)%RH范围内的实验室环境。
3 测量系统设计
本文所设计的测量系统分为两部分:用于采集原始数据的测量硬件和后期进行数据处理分析的测量软件。图1是折射率测量系统结构图。

图1 折射率测量系统结构Fig.1 Structure of refractive index measurement system
3.1 测量硬件性能分析
空气折射率测量系统的精度在一定程度上取决于作为后续解算的原始数据的采集精度。为此需要对测量系统中的硬件部分进行合理设计,从一体化变送器和3种环境传感器的选型这两个方面进行考虑。
在解算空气折射率时,要求用于解算的3个环境参数原始数据必须在时间上同步。
图2为变送器模型图,变送器底部的探测器接口可以根据不同的精度要求,选用合适的传感器进行环境参数测量,使得测量系统具有更好的可扩展性。

图2 变送器模型图Fig.2 Transmitter model diagram
测量系统使用硅基微机械压力传感器进行压强数据的采集。这种传感器集合单晶硅材料和电容式测量两种先进技术于一体,具有较低的迟滞性、卓越的测量精度和长期稳定性。
铂电阻RTD传感器是目前较为稳定和精准的温度传感器,其线性度优于热偶和热敏电阻,能够满足测量系统对于温度测量的性能要求。测量系统在进行湿度测量时使用了最新的薄膜电容型湿度传感器。该类传感器在冷凝和高浓度环境下也能正常测量。
这3种环境传感器经过国家质检单位进行精度标定后,压力传感器在-40~60 ℃的温度条件下的采集精度为±0.01 kPa;温度传感器的采集准确度在0.2 ℃内;湿度传感器在0~40%RH时的测量不确定度保持在0.6%RH,采集准确度保持在1%RH范围内。
该测量系统硬件部分在实际使用时具有小型便携的使用特性。测量硬件部分只能进行简单的环境信息的感知采集,并不能实现空气折射率的解算和精度分析。在整个测量系统中,测量软件则能够对原始数据进行处理分析,从而解算出有效的空气折射率信息。
3.2 测量软件架构设计
测量系统软件采用面向对象编程的C Sharp程序设计语言,选用稳定的.NET Frameworks 4.0作为基础开发框架,基于Windows Form桌面应用程序框架开发进行软件界面设计,进而实现对系统软件功能的快速迭代。
该系统软件在并行采集和实时显示上,采用基于线程池模型的轻量级并行编程技术进行性能优化。在数据持久化管理上,采用微软支持的关系型数据库Microsoft Access来实现数据的存储和管理。图3为测量系统软件功能设计图。

图3 测量系统软件功能结构Fig.3 Functional structure of measuring system software
该系统软件需要进行通信的硬件是用于原始数据采集的一体化变送器和用于验证系统精度的常用干涉仪补偿器。计算机和测量硬件之间通过RS232和USB接口进行物理连接,两者的通信交互采用符合可交换虚拟仪器规范的VISA COM I/O通信基础类库进行实现。为了更好地实现与硬件的通信操作,将一体化变送器和环境补偿器的相关属性和通信动作封装成对应的通信器类,并使用经典的单例设计模式保证软件中每种通信器实例的唯一性[15]。
测量软件能够对硬件部分采集的原始数据进行实时记录,并使用空气折射率运算库进行循环处理和解算。在软件中集成3种PTF测量公式的在线运算和离线运算功能,并支持两种激光波长的自定义设置,从而实现多波长空气折射率的同时运算,除此之外,软件还包含测量系统的精度分析功能,为测量系统的整体精度提供保证。
4 实验验证及分析
该测量系统经过更高精度的校准装置校准后,从数据采集性能和不同解算公式的精度两个方面对其进行合理分析。
在压强为100.17~100.21 kPa,温度为21.1~21.9 ℃,湿度为(45.9~58.0)%RH的恒温恒压环境下进行测量实验。综合考虑两种测量装置的响应时间限制后,设置采样间隔为30 s,采样次数为50次,测量总时长为25 min。
4.1 数据采集性能分析
将高精度折射率测量系统(简称测量系统)和环境补偿器(简称补偿器)在同一实验室环境下进行测量工作,在测量软件中获取两种测量装置的原始数据,并进行必要的对比分析。
4.1.1 压强采集性能分析
补偿器的压强采集精度一般在±0.1 kPa,低于测量系统采用的压力传感器精度(±0.01 kPa)。如图4所示,补偿器不能很好地感知到10 Pa内的压强变化,而测量系统则能够探测到1 Pa左右的压强变化。相比之下后者的测量数据更能反映压强变化的真实情况。

图4 压强测量数据对比Fig.4 Comparisons of pressure measurement data
使用平均值和均方根误差对测量系统和补偿器测得的压强数据进行分析。其中,相对误差是指补偿器和测量系统在同一时刻的测量值之差,具体如表3所示。

表3 压强采集数据分析Tab.3 Analysis of pressure acquisition data kPa
4.1.2 温度采集性能分析
测量系统的铂电阻RTD传感器和补偿器的理论精度比较相近,为0.2 ℃。在实际测量中,用于测量温度的探头受到环境温度的影响具有一定的延迟时间,如图5所示,两个采集装置在刚开始测量时示值并不稳定,大约10 min左右后稳定在特定值附近。

图5 温度测量数据对比Fig.5 Comparison of temperature measurement data
使用平均值和均方根误差来对变送器和补偿器测得的温度数据进行分析,如表4所示。

表4 温度采集数据分析Tab.4 Comparisons of temperature acquisition data
4.1.3 湿度采集性能分析
测量系统的湿度传感器精度为1%RH,补偿器的温度采集精度为±6%RH。如图6所示,测量系统和补偿器的湿度采集数据的变化趋势相近,即两者对于湿度的动态响应能力相近。但是由于采集精度的限制,该测量系统的采集数据更加接近实际环境的相对湿度(50%RH)。
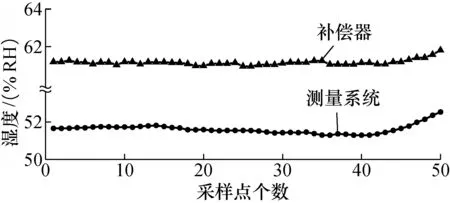
图6 湿度测量数据对比Fig.6 Comparison of humidity measurement data
使用平均值和均方根误差来对测量系统和补偿器测得的湿度数据进行分析,如表5所示。

表5 湿度采集数据分析
4.1.4 整体采集性能分析
综合考虑3种环境参数对空气折射率解算结果的影响,对测量系统的整体采集性能进行分析。基于Birch间接测量公式,采用单一变量法进行仿真分析。为了更好反映这些物理量之间的关系,将解算公式进行简化[16],表达式如下所示:
n=-a1t-a2r+a3p
(7)
式中:a1=0.94×10-6℃;a2=0.87×10-6;a3=0.24×10-8Pa;t,r,p分别表示温度、相对湿度和气压;当3者对应的系统误差分别为Δt、Δr和Δp时,其所引起的空气折射率测量的系统误差为Δn。则结合式(6)可以得出折射率测量时存在的系统误差的估算公式为
|Δn|=|a1Δt|+|a2Δr|+|a3Δp|
(8)
综上所述,测量系统相对于补偿器,压强测量上减少了0.14 kPa的偏差,温度测量上减少了0.092 ℃的偏差,湿度测量上减少了9.55%RH的偏差。由式(8)可知,空气折射率的理论测量误差在5.06×10-7附近。以上只考虑Birch公式进行解算时的误差,当使用不同的间接测量解算公式时,折射率偏差理论上保持在2.53×10-7以内。
测量系统软件对实验采集到的原始数据采用Birch公式进行解算,结果如图7所示。

图7 Birch公式对两种原始数据解算结果对比Fig.7 Comparison of Birch formula’s solution results for two kinds of raw data
测量系统的空气折射率测量平均值为1+2.672 8×10-4,补偿器的测量平均值为1+2.675 5×10-4。与补偿器相比,测量系统的实际测量误差减少了2.7×10-7。
4.2 解算公式精度分析
在空气折射率测量过程中,除了对数据采集性能进行分析,还应该考虑解算公式选择对测量结果精度的影响。
测量系统软件对实验采集的原始数据进行实时分析,得到的折射率解算结果如图8所示。3种解算结果的变化趋势大致相同,说明3者都能实时反映出空气折射率的变化情况。

图8 不同公式对变送器数据的解算结果对比Fig.8 Comparisons of the Solution Results of Different Formulas for Transmitter Data
为了更直观地比较出解算公式的优劣,分别计算出Bönsch公式与Edlen公式、Birch公式与Edlen公式、Birch公式与Bönsch公式之间的误差,并取误差平均值作为分析标准,结果见表6。

表6 解算公式误差分析Tab.6 Error analysis of solution formula
从表6可以看出前两者的误差平均值都大于0.03×10-6,而Birch公式和Bönsch公式的误差仅为0.006×10-6,说明原始Edlén公式的实际精度相对偏低。而Bönsch公式的拟合数据涉及到波长的影响,并且理论精度较高,可以应用于多种波长的激光测量中。在实际测量过程中使用该公式可以减少解算公式带来的误差。
5 结 论
通过空气折射率测量系统和常用补偿器同时采集到的原始数据的对比分析,证明在压强为100.17~100.21 kPa,温度为21.1~21.9 ℃,湿度为(45.9~58.0)%RH的实验条件下,该测量系统相对于常用环境补偿器,实际测量误差降低了2.69×10-7。该测量系统可以应用到各种类型激光干涉仪测量的环境补偿中,从而间接地提高位移测量精度。

