面向机器人标定的单激光跟踪仪顺序多站式测量系统建模与分析

乔贵方, 孙大林, 温秀兰, 宋光明, 张 颖, 宋爱国

(1. 南京工程学院自动化学院，江苏南京211167； 2. 东南大学仪器科学与工程学院，江苏南京210096)

1 引 言

近年来，工业机器人在高端制造领域的应用受到了国内外广泛关注[1,2]。欧盟于2010年至2013年资助的COMET项目，提出了研究工业机器人在机械加工方面的关键技术，其目标是实现高精度、低成本、柔性化的加工系统[3]。南京航空航天大学廖文和研究团队[4]以及天津大学邾继贵研究团队[5]等近些年重点研究将工业机器人应用于航天工业的钻铆/装配作业以及制造现场的在线测量系统等高端制造领域。

目前工业机器人的重复定位精度虽能达到0.01～0.1 mm，但其绝对定位精度仍仅为mm级，这限制了工业机器人在高端制造业的应用。通过机器人标定技术能够有效提高机器人的精度性能[6～9]。目前机器人标定技术中常用的测量设备有三维视觉测量、激光干涉仪、球杆仪以及激光跟踪仪等[10]。其中激光跟踪仪应用较为广泛, 具有测量精度高、范围大等特点[11,12]。激光跟踪仪的测距精度在全量程范围内的误差为0.01 mm，但其测量精度受限于编码器误差，激光跟踪仪的测量不确定度随测量距离的增加而增大[13]。

为利用激光跟踪仪距离测量的高精度特性，一些学者提出多边测量方法，该方法仅利用距离信息便可以求解出目标点的空间坐标[14,15]。研究人员针对该测量系统的自标定等方面展开了深入的研究，如天津大学张国雄等利用四路激光干涉仪实现了多站式测量系统的自标定和测量，并讨论了系统布局对自标定及测量精度的影响[16,17]；杜伦大学Zhang D等通过数值仿真讨论了不同基站布局、不同基站数量的多站式测量系统自标定的不确定度[18]；萨拉戈萨大学Aguado S和Conte J等研究测量误差、激光跟踪仪的布局等因素对多站式测量系统自标定的影响，探讨了多站式系统的最优布局[19,20]。

多路激光测量系统需要同时使用多个激光跟踪仪或激光干涉仪，测量系统造价较高。因此，许多学者研究提出顺序多站式测量系统，该系统仅利用一台激光跟踪仪或激光干涉仪在不同位置测量目标点。

西安交通大学郭俊杰等利用顺序多站式测量系统实现了数控机床的误差标定[21,22]；哈尔滨工业大学深圳研究院胡泓等就利用四路激光跟踪仪构建顺序多站式测量方法，实现了对三轴数控机床的几何误差测量[23]；北京工业大学陈洪芳等利用五路激光跟踪仪构建顺序多站式测量系统，实现了对大型齿轮关键尺寸的精确测量[24]；英国巴斯大学Muelaner J等利用激光跟踪仪搭建顺序多站式测量系统实现了IGPS系统的标定[25]。顺序多站式测量系统主要应用于大尺寸高精度测量，对于测量点固定或运动重复性较好的测量对象具有较好的适应性[26]。

本文针对应用于大型串联工业机器人标定的单激光跟踪仪顺序多站式测量系统进行建模与分析，首先通过测量系统的建模与仿真分析确定适用于机器人标定的最优系统配置，然后搭建相关的实验平台，验证顺序多站式系统的测量性能。

2 顺序多站式测量系统及方法

2.1 激光跟踪仪顺序多站式测量系统

图1为本文所搭建的激光跟踪仪顺序多站式测量系统。

图1 顺序多站式测量系统的示意图Fig.1 Schematic diagram of sequential multilateration measurement system

测量系统使用的激光跟踪仪为Leica AT930，在60 m范围内的测量不确定度为±(15 μm+6Lμm/m)(L为测量距离，m)。配套使用的测量软件为Spatial Analyzer软件，该软件提供了包括拟合几何体、建立坐标系等功能。该系统待标定的工业机器人为埃夫特ER10L-C10六自由度工业机器人，末端负载为10 kg，重复定位精度为±0.05 mm。靶球安装在工业机器人的末端法兰盘。测量过程符合ISO9283及GB/T 12642—2013[27]工业机器人性能规范及其试验方法标准。

2.2 激光跟踪仪的多边测量方法

多边测量系统一般要求具有4个测量设备同时测量目标点。图2为利用四路激光跟踪仪所构成的典型多站式测量系统。

图2 多边测量方法示意图Fig.2 Schematic diagram of multi-lateration measurement method.

图2中Pi为待测量的目标点，i=1,2,…,n；PBj定义为激光跟踪仪的位置，又称为基站位置，j=1,2,3,4。

4个基站位置的激光跟踪仪能够同时测量目标点到激光跟踪仪的距离Lij。因此，单个目标点能够建立等式(1):

(1)

式中：Lij为四路激光跟踪仪测得目标点Pi的距离；目标点Pi的坐标为(xi,yi,zi)；基站位置PBj的坐标为(xBj,yBj,zBj)。

若基站位置PBj的坐标已知，即可计算出目标点Pi的坐标。但激光跟踪仪的安装位置无法精确测量，导致目标点Pi的坐标计算误差较大。通过观察式(1)可知，每增加1个目标点会引入3个未知变量，但能够新增4个约束。因此，当目标点个数大于12时，即可建立超定方程组。但由于仪器测量误差的存在，无法直接计算出未知变量。通常构建如式(2)所示的目标函数J，并利用最小二乘法等优化算法计算基站位置PBj的坐标，此过程称为系统自标定。

(2)

式中：fij为残差,见式(3)；m为目标点的个数；n为激光跟踪仪数量。

(3)

3 顺序多站式测量系统建模与分析

顺序多站式系统是基于多边测量方法，但该系统仅需要一台激光跟踪仪，从而大大降低了测量系统的造价。顺序多站式系统的测量过程如下：1)将激光跟踪仪依次放置在不同基站位置，在每个基站位置上重复测量自标定目标点和测量目标点；2)依据自标定目标点的数据和自标定方法精确计算基站位置；3)根据获得的基站位置计算测量目标点的坐标。文献[21]中利用顺序多站式系统实现对中高档数控机床的几何参数误差标定，但串联工业机器人的定位精度相比与中高档数控机床较差。鉴于此方面不足，首先建立测量系统的仿真模型，分析工业机器人定位精度、测量点的数量/位置/分布形状以及激光跟踪仪的基站布局对测量精度的影响；然后再根据分析结果搭建物理实验系统。

3.1 测量系统的仿真条件配置

3.1.1 工业机器人定位精度性能建模

在ISO-9283及GB/T 12642—2013[27]标准中，定义重复定位精度是对同一指令位姿从同一方向重复响应n(n≥30)次后得到位姿的一致程度。位置重复性RPr可由式(4)计算得出:

(4)

式中：xj，yj，zj为测量的坐标数据;j=1,…,30。

测量得到ER10L-C10机器人在空载情况下的重复定位误差为0.025 2 mm。为了尽可能地模拟实际的重复定位误差分布，本文分析了30个被测点距其集群中心在x，y，z三轴的分布情况，利用Matlab中的ksdensity函数求取各轴向上误差分布的概率密度，如图3所示。

图3 工业机器人定位误差概率分布Fig.3 Probability distribution of positional errors of industrial robots

利用相应的分布函数确定ER10L-C10机器人在3个轴线方向上的重复定位误差，将其应用于测量系统的模型中，使该系统模型具有较好的拟真性。

3.1.2 激光跟踪仪测量精度性能建模

激光跟踪仪同样存在测量误差，利用SA测量软件计算得到激光跟踪仪的距离测量不确定度为0.003 mm。因此，认为激光跟踪仪的测量误差在区间[-0.003, 0.003]内服从均匀分布。

3.2 影响系统自标定精度的因素分析

根据文献[7～13]的研究可知，自标定目标点的数量、距离、分布形状、重复定位精度及激光跟踪仪安放位置都对自标定精度影响较大。本文建立的仿真测量系统如图4所示。

图4 仿真分析中的测量系统配置Fig.4 Measurement system configuration in simulation analysis

3.2.1 目标点的数量对自标定精度的影响分析

除了完善企业资金监管机制之外，电力企业还需要建立健全资金风险预警机制，尤其是建立重大事件预防和突发事前预警机制，以提升企业防范和应对运营风险和财务风险的能力。电力企业可以通过宣传、教育、培训等途径，加强企业内部人员的风险防范意识。同时，建立科学的资金风险预警机制，充分利用风险控制、风险转移、风险规避等风险防范措施，做到事前预防资金风险、事中识别和评估资金风险、事后及时应对资金风险，以降低电力企业经营风险和财务风险发生的可能性，并尽可能将风险损失降至较低水平。

理论上自标定目标点的数量越多，计算得到的基站位置精度越高。但增加目标点数量的同时也会引入更多的误差。因此，在标准仿真条件下仅改变测量点数量，分别为25，64，100，144，196。自标定的仿真结果如图5所示。

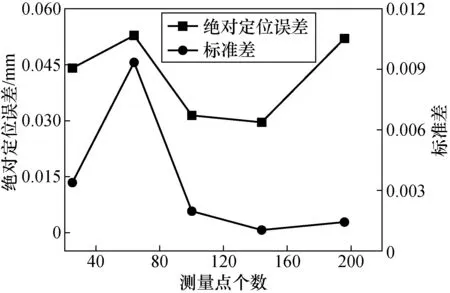
图5 目标点测量数量对自标定的影响Fig.5 The influence of measurement quantity of the target points on self-calibration.

从图5可以看出，随着目标点数量的增加，测量系统自标定的精度和稳定性相差较大。其中目标点的数量为144时，测量系统的自标定精度较好，并且自标定稳定性较好;而当继续增加目标点的数量时，测量系统的自标定精度下降。

3.2.2 目标点的测量距离对自标定精度的影响

首先将标准仿真条件下测量点平面定义为平面3；然后沿平面3法线方向向前移动400 mm，800 mm分别形成平面4和平面5；再向后移动400 mm，800 mm 分别形成平面2和平面1。分别针对这5个平面进行仿真分析，测量系统自标定的结果如图6所示。当目标点测量距离为2 500 mm时，自标定的精度和稳定性最好。而当目标点的测量距离在 3 000 mm 左右时，自标定的精度和稳定性较差。但自标定误差的波动区间较小，也说明了测量距离对自标定的影响较小。

图6 目标点测量距离对自标定的影响Fig.6 The influence of measurement distance of the target points on self-calibration.

3.2.3 目标点的分布对自标定精度的影响

将自标定目标点的分布形状分为平面和立体两种情况讨论，其中平面分布又分为正方形和圆形两种。当自标定目标点的分布形状为正方形时，分布面积分别设置为0.62m2，0.72m2，0.82m2，0.92m2，1 m2。自标定的仿真结果如图7所示。

图7 目标点正方形分布对自标定的影响Fig.7 The influence of square distribution of the target points on self-calibration.

随目标点分布面积增加，自标定的稳定性增大。而当分布面积为0.64 m2时自标定精度最大。当自标定目标点的分布形状为圆形时，分布面积分别设置为 π×0.32m2， π×0.42m2， π×0.52m2， π×0.62m2， π×0.72m2。自标定的仿真结果如图8所示。随着面积的增大，自标定精度在 π×0.49 m2时最小。从图7和图8中也看出，当分布形状为平面情况时，误差波动范围较小。当自标定目标点的分布形状为正方体时，分布体积为0.63m3，0.73m3，0.83m3，0.93m3，1.0 m3。自标定的仿真结果如图9所示。随着分布体积的增加，自标定的误差先增大再减小，当分布体积为1.0 m3时自标定误差最小，且误差波动区间同样较小。

图8 圆形目标点分布对自标定的影响Fig.8 The influence of circular distribution of the target points on self-calibration.

图9 目标点正方体分布对自标定的影响Fig.9 The influence of cube distribution of the target points on self-calibration.

由于顺序多站式测量系统仅使用一台激光跟踪仪，依次放置在4个基站位置测量工业机器人的同一批自标定目标点。工业机器人的重复定位精度严重会影响目标点的重合度，因此需要分析重复定位精度大于多大阈值时将不适用顺序多站式测量系统。因此，将工业机器人的重复定位误差设置为标准值的1～5倍。自标定的仿真结果如图10所示。随着机器人重复定位误差的增加，自标定误差也随之增大，两者之间基本呈线性关系，因此，顺序多站式测量系统的性能比多站式测量系统差。

本文拟合目标点重复定位误差与自标定误差的函数关系式，并结合激光跟踪仪的测量不确定度Us为：

Us=15 μm+6Lμm/m

(5)

式中L为测量距离，单位为m。

图10 目标点的重复定位误差对自标定的影响Fig.10 The influence of repetitive positional errors of the target points on self-calibration.

当目标点的重复定位精度小于0.045 mm时，顺序多站式测量系统优于单站式测量系统。

3.2.5 激光跟踪仪分布位置对自标定精度的影响

激光跟踪仪的分布位置对多站式系统的自标定有较大影响[7～13]。文献[7,10]分别提出正四面体和直三棱锥两种基站位置分布形状。为确定何种分布适用于机器人标定，本文建立如图11所示的两种基站位置分布及自标定的影响，对于本文所使用的工业机器人来说，正四面体分布要优于直三棱锥分布，自标定误差更低并且稳定性更好。

图11 激光跟踪仪对位置分布和对自标定的影响Fig.11 The influence of the laser tracker location on self-calibration.

激光跟踪仪基站位置的初始值确定是影响测量系统自标定过程中优化的主要因素之一。目前多站式测量系统的世界坐标系通常有两种：(1)由激光跟踪仪的基站位置构建世界坐标系，此种方法能够减少自标定参数的数量，但激光跟踪仪的初始位置不易测量；(2)选择测量系统中其他已有的坐标系，本文选取工业机器人的基坐标系作为测量系统的坐标系，激光跟踪仪每放置在一个基站位置上均完成与工业机器人基坐标系的转换，这样可以获得较为精确的基站位置初值，有利于提升顺序多站式测量系统的自标定精度，在后期机器人标定过程中无需再进行坐标系的转换。

4 顺序多站式测量系统测试实验

4.1 测量系统的搭建方案

基于以上仿真分析结果，自标定目标点的数量设置为140，测量距离为2.5 m。目标点的分布形状对自标定精度的影响相对较小，因此，在机器人标定中可不单独设置自标定目标点，直接使用机器人末端位置的测量点。由于正四面体对测量距离以及边长有一定约束，并且受激光跟踪仪自身调高限制，本文采用直三棱锥的基站位置布局。

4.2 测量系统的性能测试

本文搭建的单激光跟踪仪顺序多站式测量系统如图12所示。图12中激光跟踪仪依次放置在位置1，2，3，4处。

图12 单激光跟踪仪的顺序多站式测量系统Fig.12 Sequential multi-lateration measurement system of the single laser tracker

工业机器人从零位状态开始运动，分别单独绕轴1旋转80°，绕轴2旋转100°，绕轴3旋转100°，旋转步长为1°。激光跟踪仪在每个基站位置上测量机器人末端安装的靶球坐标向量Pm，并读取示教器中的靶球的坐标向量Pr。记Pmi和Pri为激光跟踪仪在基站位置i时测量和读取的机器人末端坐标向量。Pmi和Pri理论上为同一组点在不同坐标系下的坐标向量，应满足式(6)。

Pri=miRri·Pmi

(6)

fi=min∑(miRri·Pmi-Pri)

(7)

将激光跟踪仪的基站位置坐标向量Ti和求解得到的目标点在机器人坐标系下的平均坐标Pra，作为自标定的初值带入式(2)，并用最小二乘算法求解使J最小的激光跟踪仪的4个基站位置坐标向量Ti及目标点在机器人坐标系下的坐标向量Pri。

为验证顺序多站式测量系统的测量精度，将两个紧贴的靶球中心距作为标准长度，靶球的半径为(19.05±0.002 5) mm，靶球的中心偏差小于±0.003 mm，靶球的形状偏差小于±0.001 5 mm。利用本文自标定后的顺序多站式测量系统对两个靶球中心距进行测量，得到的测量误差为0.023 mm，同样条件的仿真的结果为0.01 m，如图13所示。

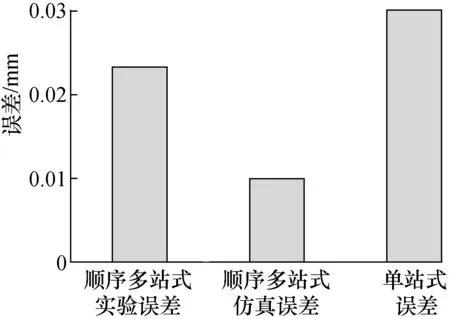
图13 顺序多站式测量系统的测量精度对比Fig.13 Comparison of the measurement accuracy of the proposed sequential multi-lateration measurement system.

实验与仿真分析的结果相差较大，原因是激光跟踪仪的基站位置无法严格的按照正三棱锥的位置摆放，同时也存在其他不可预知的误差因素。根据式(5)可知，单站式激光跟踪仪的测量不确定度为0.03 mm。

5 结 论

为提高工业机器人参数标定的精度，本文提出一种基于单台激光跟踪仪的顺序多站式测量系统。首先，建立了该测量系统的仿真模型，并分析了自标定目标点的数量、测量距离、分布形状、基站位置以及工业机器人重复定位精度对自标定过程的影响，仿真分析结果表明：顺序多站式测量系统能够适用于工业机器人的参数标定，但要求工业机器人的重复定位精度优于0.045 mm。然后，依据测量系统的仿真结果，搭建了应用于工业机器人标定的顺序多站式测量实验系统。通过实验得到该测量系统的测量误差为0.023 mm，优于单站式激光跟踪仪测量误差，能够满足大型串联工业机器人参数标定的精度需求。课题组将在后续工作中对如何进一步优化顺序多站式测量系统的测量精度和降低系统搭建的复杂性做进一步研究。