分数阶Fornberg-Whitham型方程的解析解及其演化现象

张 慧

(西南科技大学 城市学院，四川 绵阳 621000)

在过去的几十年里，越来越多的学者开始关注分数阶非线性偏微分模型，与整数阶模型相比，分数阶导数模型具有全局相关性，能够充分地描述事物发展的历史依赖过程，比如，时间分数阶波方程就能描述时间的记忆性； 空间分数阶扩散方程可以刻画反常扩散现象、慢扩散现象、快扩散现象和超扩散现象等； 时间-空间分数阶偏微分方程可以准确地描述各种复杂运动的中间过程，例如，水分子向土壤的入渗以及非饱和水在土壤中的运移模型.

分数阶非线性偏微分方程的解法研究，一直是力学、工程技术学、物理学、生命科学和应用数学等领域的工作者致力于研究的最为活跃的课题之一.因此，许多有效的求解方法也被陆续地提出来，包括Adomian分解法[1]、首次积分法[2]、同伦分析法[3]、李群理论方法[4]、不变子空间方法[5]、分式变分迭代法[6]、分数复变换法[7]、分离变量法[8]、Laplace变换法[9]以及分离变量法与齐次平衡原理相结合的方法[10]等.

1967年，在文献[11 ]中B.Fornberg和Whitham提出了经典的非线性偏微分Fornberg-Whitham方程

ut-uxxt+ux=uuxxx-uux+3uxuxx.

(1)

该方程可以描述定性的碎波现象.许多学者对该方程进行了研究，其中Fornberg 和 Whitham获得了非线性Fornberg-Whitham方程的尖波解.Abidi和Lu等在[12-13]中分别使用同伦摄动法，变分迭代法和Adomian分解法研究了该方程的解析解，Gupta,Sakar[14-15]等研究了该方程的逼近解. Sahadevan和Prakash[16]利用不变子空间的方法研究了时间分数阶 Fornberg-Whitham 方程的精确解.而对于分数阶Fornberg-Whitham 方程的研究目前文献中比较少，本文在变量分离法与齐次平衡原理相结合的方法的基础上，对解的假设结构稍加改进，使其更具有普适性，并且求解方法和技巧较之前文献中的要简便许多.

文献[17]中解的假设结构u=a0+a1v(x)Eα(λtα)只适合求解Caputo型分数阶导数定义下的分数阶偏微分方程，因为常数a0在黎曼-刘维尔型分数阶导数的定义下求导不为零. 因此，我们对这种解的假设结构稍作改进为u=(b0+b1v(x))Eα(λtα)，可以同时适应黎曼-刘维尔型和Caputo型二种分数阶导数定义下的分数阶偏微分方程的求解，然后利用改进后的算法分别研究时间分数阶、空间分数阶以及时间-空间分数阶三类非线性偏微分Fornberg-Whitham方程的精确解及其演化现象.

首先给出关于分数阶微积分的2种常用的定义及其性质，以方便读者更好的理解，更多细节参考文献[18-19].

黎曼-刘维尔分数阶导数定义如下：

(2)

其中n=[α]+1,n-1≤αa≥0,[α]表示的是非负实数α的整数部分.

(3)

其中n=[α]+1,n-1≤αa≥0,且f(t)连续n阶可导.

有关分数阶导数和积分的常用性质有：

(4)

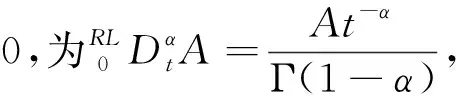
1 时间分数阶Fornberg-Whitham型方程的精确解及其动力学性质

本节将利用改进后的齐次平衡原理与分离变量相结合的方法来研究时间分数阶Fornberg-Whitham型方程：

(5)

的精确解，其中u=u(x,t),t>0,x∈R，假设方程(5)具有如下形式的解

u=(b0+b1v(x))Eα(λtα),

(6)

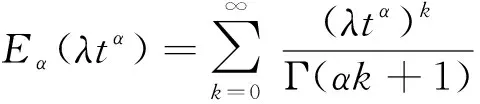
将(6)式代入方程(5)中可得

(7)

对上式进行整理可得

(8)

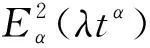
(9)

首先对方程组(9)中第1个线性常微分方程进行求解，可以得到其通解：

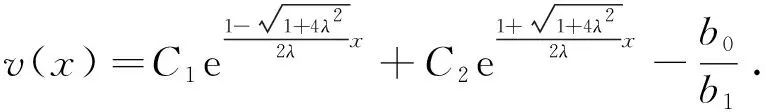
(10)

再将上式代入方程组(9)的第2个方程中可得

(11)

其中

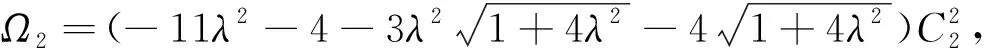
令Ω1=0，Ω2=0，Ω3=0可得：

(12)

将(12)式代入(10)式可得方程组(9)的解

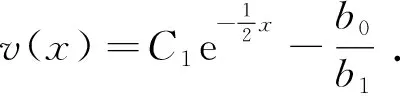
(13)

再将(14)式带入(6)中可得时间分数阶Fornberg-Whitham型方程(5)的二个精确

(14)

(15)

其中C1,b1为任意非零的常数.解(14)和(15)空间部分函数为无界函数，又当时间t趋于正无穷时，振幅随时间的增加而衰减.为了能够直观地展示解(14)和解(15)的动力性质，将其绘制成了3维坐标图形，如图1所示，在图1(a)取C1=0.2,b1=7.5,α=0.75;图1(b)中取值为C1=0.2,b1=2.5,α=0.75.

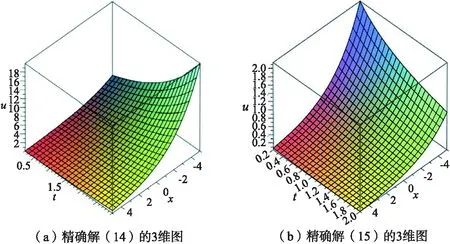
图1 解随时间和空间发展的3维坐标模拟图

2 空间分数阶Fornberg-Whitham型方程的精确解及其动力学性质

本节主要研究空间分数阶Fornberg-Whitham型方程：

(16)

的精确解，其中u=u(x,t),t>0,x∈R,0<β<1.

假设方程有如下形式的解：

u=(h0+h1w(t))Eβ(λ0tβ),

(17)

其中h0,h1,λ0是待定常数且h1≠0,λ0≠0,w=w(t)是关于t的待定函数.

同样将(17)代入(16)式中可得

(18)

将上式整理可得

(19)

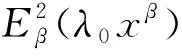
(20)

求解(20)式中的第1个常微分方程得

(21)

再将(21)代入(20)式的第2个方程中可得

(22)

(23)

因此，将(23)式代入(21)式中可得

(24)

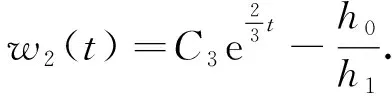
(25)

将(23)式、(24)式和(25)式代入(17)式可得空间分数阶Fornberg-Whitham型偏微分方程(16)的2个精确解

(26)

(27)

其中C3,h1为任意非零的常数.

3 时间-空间分数阶Fornberg-Whitham型方程的精确解

当时间和空间都为分数阶时，即当0<α<1,0<β<1时，方程(1)可转化为时间-空间分数阶Fornberg-Whitham型方程

(28)

其中u=u(x,t),t>0,x∈R.

我们假定方程(28)有如下形式的解

u=hEα(λ1tα)Eβ(λ2xβ)，

(29)

其中h,λ1,λ2是待定常数且h≠0,λ1≠0,λ2≠0. 将(29)代入(28)式可得

(30)

整理上式可得

(31)

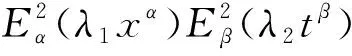
(32)

解方程组(32)可得

(33)

于是将(33)式代入(29)式中可得时间-空间分数阶Fornberg-Whitham型方程的2个精确解

(34)

(35)

其中h为任意的非零常数.解(34)和(35)同样当时间t趋于正无穷时，振幅随时间的增加而衰减.为了能够直观地展示解(34)和解(35)的动力性质，在图2(a)中绘制了解(34)取h=-6,α=0.75,β=0.75下的3维坐标图形，图2(b)中取值为h=-0.2,α=0.25,β=0.25绘制出解(35)的坐标演化图形.

图2 解(34)和解(35)的动力学行为演化图

4 结语

本文改进了文献[17]中关于解的假设结构问题，使得积分分支方法与齐次平衡原理相结合的方法在求解分数阶偏微分方程时更具普适性，即可以用它来获得Riemann-Lioville导数意义下的分数阶非线性偏微分方程的精确解，又可以获得Caputo导数意义下的分数阶非线性偏微分方程的精确解.利用改进后的算法研究了不同类别的分数阶Fornberg-Whitham 型方程的精确解，通过对所得精确解的分析，发现其中大部分解都具有随时间和空间发展而产生衰减的特性.