范德蒙行列式的2种证明及其应用

张泽锋，陈秀琴

(信阳职业技术学院 数学与计算机科学学院，河南 信阳 464000)

在《高等代数》中，定义形如

的行列式为n阶范德蒙行列式[1].范德蒙行列式不仅在数学领域有着广泛的应用，在其他领域也有着很重要的应用.

1 范德蒙行列式的新证明

求证n阶范德蒙行列式：

(1)

1.1 用数学归纳法证明

证明对n作归纳法：在n=2时，D2=x2-x1，显然式(1)正确.

假设对于n-1阶的范德蒙行列式，式(1)结论成立，下面证明式(1)对n阶的范德蒙行列式也成立.

构造一个辅助的n阶行列式D(x)：

(2)

易得D(xn)=Dn，将D(x)按照第n列展开，得：

D(x)=1·A1n+x·A2n+x2·A3n+…+xn-2·An-1n+xn-1·Ann

(3)

式(3)中，Ain(i=1，2，3，…，n)是行列式(2)中的元素ain=xi-1(i=1，2，3，…，n)的代数余子式，而且不含x.因而由式(2)可得D(x)是一个n-1次的多项式，最高次xn-1的系数是Ann，按照定义可得Ann=(-1)n+nDn-1=Dn-1.

其次，由行列式的性质可知x1,x2,x3,…，xn-1是D(x)的n-1个根，由多项式的理论可知：

D(x)=Dn-1(x-x1)(x-x2)(x-x3)…(x-xn-1)

(4)

取x=xn，代入式(3)可得：

D(xn)=Dn-1(xn-x1)(xn-x2)(xn-x3)…(xn-xn-1)

(5)

即：

Dn=D(xn)=Dn-1(xn-x1)(xn-x2)(xn-x3)…(xn-xn-1)

(6)

(7)

从而式(1)得证[2].

1.2 用定理证明

证明设n阶行列式

对式(1)从最后一行起，每一行减去它相邻的前一行的x1倍，得：

Dn=

(8)

由上述结论可知：

(9)

提取每一列的公因子后可得：

Dn=(x2-x1)(x3-x1)…(xn-x1)

(10)

式(10)中，Dn最后一个因子是n-1阶范德蒙行列式Dn-1.

则：

Dn=(x2-x1)(x3-x1)…(xn-x1)Dn-1

(11)

同理可得：

Dn-1=(x3-x2)(x4-x2)…(xn-x2)Dn-2

(12)

重复进行，最终可得[3]：

Dn=(x2-x1)(x3-x1)…(xn-x1)

(x3-x2)(x4-x2)…(xn-x2)…(xn-xn-1)=

(13)

从而式(1)得证.

2 范德蒙行列式的应用

2.1 在n阶行列式计算中的应用

在计算有些行列式时，可以把行列式进行简单的拆项或提公因式等转化为范德蒙行列式，以简化计算过程.

例1 计算n阶行列式

解构造一个n+1阶范德蒙行列式

(14)

那么：

(15)

把D(x)按照第n+1列展开得：

D(x)=1·A1n+1+x·A2n+1+x2·A3n+1+…+xn-1·Ann+1+xnAn+1n+1

(16)

式(16)中，Ain+1(i=1,2,3,…，n,n+1)是行列式(14)中的元素ain+1=xi-1(i=1,2,3,…，n+1)的代数余子式[4],而且不含有x，因而由式(14)可得D(x)是一个n次的多项式，而且xn-1的系数是Ann+1，按照定义可得Ann+1=(-1)n+n+1D=-D.

2.2 在线性变换理论中的应用

在线性变换问题中,运用范德蒙行列式可以巧妙地解答复杂的线性变换问题.

例2 设数域F上的n维向量W的线性变换t有n个互不相同的特征值λ1，λ2，…，λn，求证：与τ可交换的W的线性变换是e,τ,τ2,…，τn-1的线性组合，其中e为恒等变换.

证明由题意可设τ(αi)=λiαi(i=1,2,…,n)，δ是与τ可进行交换的线性变换，因而可得Wλ={kαi|k∈F}是δ的不变子空间[5].

令δ=xe+x1τ+x2τ2+…+xn-1τn-1，且τ(αi)=kiαi(i=1,2,…，n)，则有以下方程组：

(17)

2.3 在向量空间理论中的应用

在求解向量空间理论的问题时，直接处理比较复杂，通常借助范德蒙行列式进行转化，将问题简单化，有利于得出结论.

例3 设N是数域W上的n维向量空间，任意的正整数m≥n，证明：在N中存在m个向量，其中任意选取n个向量都线性无关.

证明由于W≅Wn，则只需要在Wn中思考.取m个向量b1=(1,2,22,…，2n-1) ,b2=(1,22,(22)2,…，(2n-1)2) ,…，bm=(1,2m,(22)m,…，(2n-1)m)，令:

1≤k1≤k2≤…≤kn≤m.

因为Dn符合范德蒙行列式，并且有Dn≠0， 所以向量bk1,bk2,…，bkn线性无关.

2.4 在多项式理论中的应用

在求解一些多项式理论的问题时，有些求根问题可以运用范德蒙行列式来处理.

例4 若φ1(x),φ2(x),…，φn-1(x)为n-1个复系数多项式，且有1+x+x2+x3+…+xn-1|(φ1(xn)+xφ2(xn)+…+xn-2φn-1(xn)),求证：φ1(1)=φ2(1)=…=φn-1(1)=0.

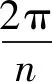
(18)

式(18)关于φ1(1)，φ2(1)，…，φn-1(1)的齐次线性方程组的系数行列式为[6]：

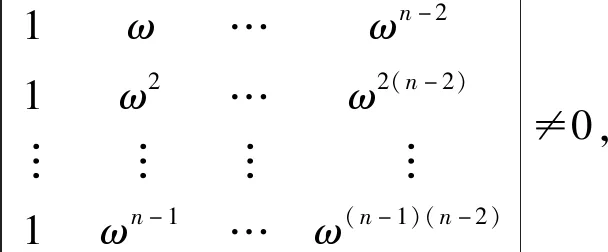
2.5 在微积分中的应用

在求解微积分尤其是在n阶导数的问题时，应用范德蒙行列式结合泰勒展开式来解决问题十分简单.

由泰勒公式得：

(19)

式(19)是有关g'(x),g"(x),…，g(n-1)(x)的线性方程组[7]，可得它的系数行列式为：

(20)

显然，式(20)的第2个行列式是范德蒙行列式，行列式的值等于1!2!…(n-1)!，所以Dn=1.

根据式(19)，可将g'(x),g"(x),…，gn-1(x)写成g(x+b)与g(n)(ξb)(b=1,2,…，n)的线性组合.

实际上，可设x≤t≤x+n，则：

(21)

2.6 在证明问题中的应用

在一些证明问题上，根据所证明问题的结构特点，将其进行简单地变形，转化为范德蒙行列式，就可以很容易得出结论[9].

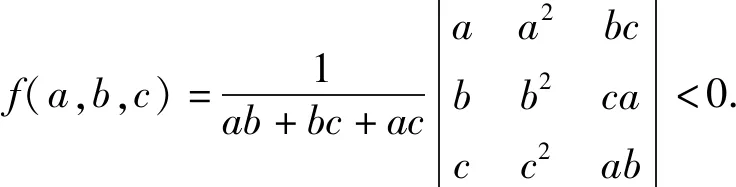
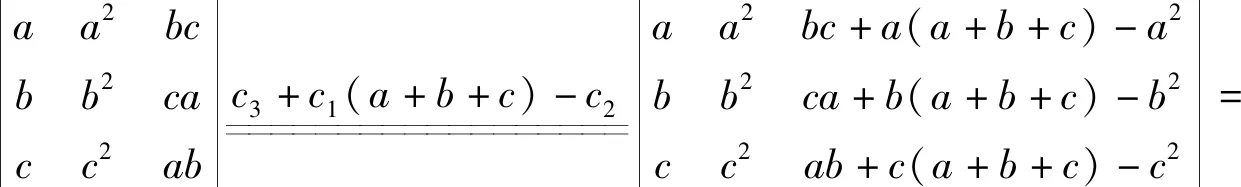
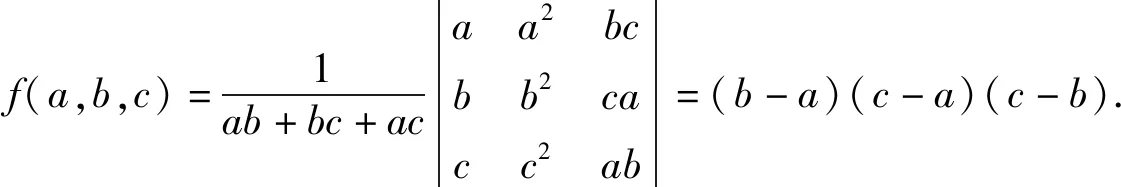
又因为a>b>c,则b-a<0,c-a<0,c-b<0，从而可得f(a,b,c)<0,命题得证.

3 结束语

范德蒙行列式为求解“数学分析”课程的一些问题提供了很好的处理方法.在学习和应用范德蒙行列式时,应该不断总结前人的经验，寻求更多关于范德蒙行列式的规律，熟能生巧,方能更好地掌握范德蒙行列式的一系列知识，以及将范德蒙行列式的相关知识更好地应用到数学各个领域的学习中.