核心素养对数学概念性知识的教学启示

文∣马晓丹

教育部《关于全面深化课程改革 落实立德树人根本任务的意见》将核心素养定义为“学生应具备的适应终身发展和社会发展需要的必备品格和关键能力”。基于这一界定展开的研究体现了以“学生发展”为核心的教育视角的变化。[1]近年来，“朝着哪一方向发展”，又该“如何发展”成为教育研究者普遍关注的问题。立足我国国情，纵览世界各国、各地区对“核心素养”的内涵解读，核心素养为新时代的教育发展提供了新的方向，新方向对学科知识的教学意义也是重大的。本文将围绕数学学科中的概念性知识教学展开讨论。

一、数学概念性知识的内涵分析

数学知识是关于数学概念的，而数学概念解释了数学世界与现实世界中存在的数学规律。[2]概念性知识包括分类和类别的知识以及它们之间的关系性知识。[3]所谓分类和类别的知识，是指基于本质特征进行分类或明确类别的准则性知识，如有一个角是直角的三角形是直角三角形，这里“有一个角是直角”是用于判断一个三角形是否直角三角形的本质特征。关系性知识是指构成同一类别知识的基本要素之间的关系，以及这些关系之间的关系。如勾股定理阐明了直角三角形三边之间的关系，这种基于关系形成的原理和通则知识可以进一步丰富个体对分类和类别知识的认识，因为满足这种三边关系的三角形也属于直角三角形。此外，“关系之间的关系”是指基于关系形成的原理和通则知识之间的关系，如勾股定理是余弦定理在夹角为90°时的特殊情况。事实上，概念性知识与程序性知识位于知识系统的连续体上，当概念性知识达到运用及以上的认知水平时，就会转化为智慧技能，也就是广义的程序性知识。

二、数学概念性知识的教学误区

当前考试多选择易于观测的外显知识进行测评，这就使得概念性知识的测评比重普遍低于程序性知识。其中，概念性知识的理解又低于概念性知识的运用。测评比重对教学的直接影响表现为对概念性知识的重视不够，特别是对概念性知识的理解重视不够。具体表现为以下三个方面。

(一)概念性知识的学习止步于记忆水平

实际教学中，概念性知识中的分类和类别知识容易与事实性知识混淆，这也是止步于记忆水平的概念教学时有发生的原因。分类和类别知识是在基本事实基础上概括出的更为抽象的知识，从基本事实要素到每一个类属关系的确立，都是远离具体细节、接近抽象领域的过程。[4]为此，寻求更高认知水平的概念教学是数学教学中的必然。举例来说，学生对有理数的认识不能止步于“记住整数和分数统称为有理数”，而是要能够解释整数、分数、有理数三者之间的从属关系，以及有限小数、无限循环小数与分数的转化关系。

(二)概念性知识的学习直接介入运用水平

直接介入运用水平的概念教学在实际教学中屡见不鲜，其原因有二。一是由于教学时间的分配并不能权衡知识学习与技能训练，表现为有意识地侧重于技能训练。这样的学习所建立的关系局限在知识的表面联系上，不能解释关系的实质。二是由于教师混淆了概念的生成过程与具体的操作步骤，表现为无意识地用操作过程代替生成过程。如条形统计图的教学常用“如何绘制轴、如何确定距离和宽度”等替代从象形统计图到条形统计图的“进化”过程。这样的学习割裂了学习者已有认知基础与新概念之间的联系。

(三)概念性知识达到高阶思维水平后出现的低阶思维水平的丧失

由于绝大多数教学的目的都指向学习的迁移，教育的重心便不会只停留在低阶思维水平，而是会向高阶思维水平转移。当概念性知识的学习经过“理解”水平后，达到“运用”及以上水平，却不能清楚地说明构成概念的基本要素之间的关系时，就会表现出低阶思维水平的丧失，也就是“会而不懂”的现象。究其原因，主要在于对“理解”的认识是片面的。在认知学习中，理解是重要的，但无论理解是作为手段还是目的，都不是唯一的。[5]修订版布卢姆教育目标分类学认为，用于判定学习者“理解”的标准是能否从多种形式的教学信息中建构意义。[6]为了实现意义的建构，“理解”涉及多个层次的认知过程。其中，“总结”“推断”“比较”“说明”是比“解释”“举例”“分类”更高层次的理解，理解得越深入，越不容易在形成高阶思维后出现低阶思维水平的丧失。

三、核心素养对数学概念性知识的教学启示

面对核心素养所引领的教学变革，数学概念性知识的教学应当走出误区，并从以下三个方面寻求改进。

(一)实施有意义的概念教学以促进学生的终身发展

核心素养视角下的“学生发展”指向了终身发展。已有研究普遍认同“核心素养的获得是一个持续的、终身的学习过程”[7]，学生需要在一个持续学习的过程中不断实现有意义的建构，即通过新经验与原有知识经验的相互作用，来充实、丰富和改造自己的知识经验[8]。奥苏泊尔认为知识和意义是等价的，他用同化思想解释了陈述性知识的学习，强调了认知结构中的原有适当观念对新知识学习的决定作用。[9]记忆、理解水平的数学概念性知识所对应的学习结果是用于回答“数学基本要素、对象或类别是什么”的陈述性知识，新旧知识的相互作用也是有意义的概念学习的重要保障。指向终身发展的数学概念性知识不仅要发挥已有知识经验对当前概念学习的固定作用，还要发挥当前概念学习对未来学习的铺垫作用。因此，这种既勾连过去，又通达未来的概念“链”，反映的是学习者对自身认知结构进行有意义建构的过程。同时，这也是一个由具体指向抽象的过程，一端连接学习者的学习起点，始于知觉辨别；另一端则可以无限延伸，进行更为抽象的思维操作。根据抽象程度的不同，概念可以分为两类：一类是从具体例证出发，依据事物的本质属性给出的描述性定义，即具体概念，通常用于概念学习的初级阶段；另一类是直接给出的定义性概念，通常用于概念的进一步学习。后者显然不能孤立于许多旧概念，定义性概念之间是相互联系的。[10]当然，数学概念学习不可只停留在具体、直观、视觉化的阶段，必须升华、逐级地反省抽象，最后完成数学概念的建构。[11]因此，具体概念的学习终将走向定义性概念的学习，并成为定义性概念学习的前提条件。可见，学习者持续的、终身的学习过程需要对同一概念进行多次建构。当前中小学数学课程的设置普遍受到“知识螺旋式上升”这一理念的影响，概念的抽象性差异成为不同学段重复学习同一概念的原因之一。如小学阶段学习圆的概念是以具体概念的形式给出的，到了中学阶段就是以定义性概念的形式给出。抽象性的不同使建立起的有意义的联系也是不同的(如图1所示)。对于具体概念而言，需要在大量事实例证中辨别当前学习的概念与易混概念，如明确圆不同于多边形的本质属性是曲线图形，圆不同于圆柱、球的本质属性是平面图形；对于定义性概念来说，则需要建立起当前学习的概念与已有概念之间的联系，如定点、定长等是与圆、圆心、半径的定义性概念相关的旧概念。

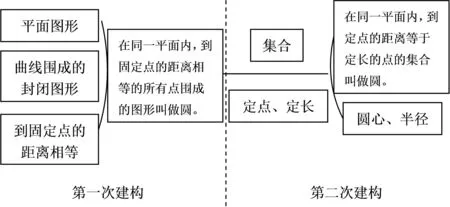
图1 圆的概念在不同学段的建构过程

(二)打通双向联系的概念教学以促进学生的全面发展

核心素养视角下的“学生发展”指向了全面发展。核心素养根植于知识、能力，却比知识、能力更为丰富，是知识、能力、态度的综合化形态。[12]全面发展所需的综合化形态的知识是问题解决的必要条件。如若运用数学概念去解决问题，离散的、链状的数学概念就应该朝着更为复杂的整块形式的知识发展。现代认知心理学将这种复杂的整块知识称为图式[13]，它在建构、反思的基础上形成，并最终用于问题解决[14]，它所表征的数学概念，应当在阐明构成概念的基本要素之间的联系(内部的)基础之上，进一步阐释概念与概念之间的联系(外部的)。如圆与圆之间的关系可以根据圆心的位置和半径的大小确定(同圆、等圆、同心圆等)，还可以根据圆心的距离与半径的和差关系来确定(相离、外切、相交、内切等)。此时，所形成的概念图式不再是离散的单点结构，而是逐步将大脑中碎片化的知识网络化[15]，最终实现一个整体在不同情境间的自由迁移。因此，运用数学概念解决问题的过程是陈述性知识向智慧技能转化的过程，高水平的认知过程(运用、分析、评价、创造)对这一转化过程起到积极的促进作用。反之，智慧技能也会对数学概念的学习起到促进作用。如运用方格纸对不规则图形(脚印、地图、树叶等)进行度量，本质上就是在问题解决的过程中进一步认识面积的本质，即用面积单位的个数来衡量面的大小。

(三)实现有深度的概念教学以促进学生的深化发展

核心素养视角下的“学生发展”指向了深化发展。作为数学教育重要目标之一的概念性理解[16]，其理解的深度不能停留在表面，而应该朝概念的本质深入挖掘。“理解”能够促进新知识与已有心理图式和认知框架的整合，这也是概念性知识与认知过程“理解”之间存在惯性搭配的原因。课题组调研发现，在数学教学设计中，用“解释”“举例”“分类”等认知过程来达成概念性知识理解水平的现象是较为普遍的。之所以说对“理解”水平的认识是片面的，一方面原因在于，忽视了“理解”水平是多种认知过程共同作用的结果。除了“解释”“举例”“分类”之外，“总结”“推断”“比较”“说明”也是“理解”类别中的认知过程[17]，不同认知过程中数学概念性知识的例子如表1所示。

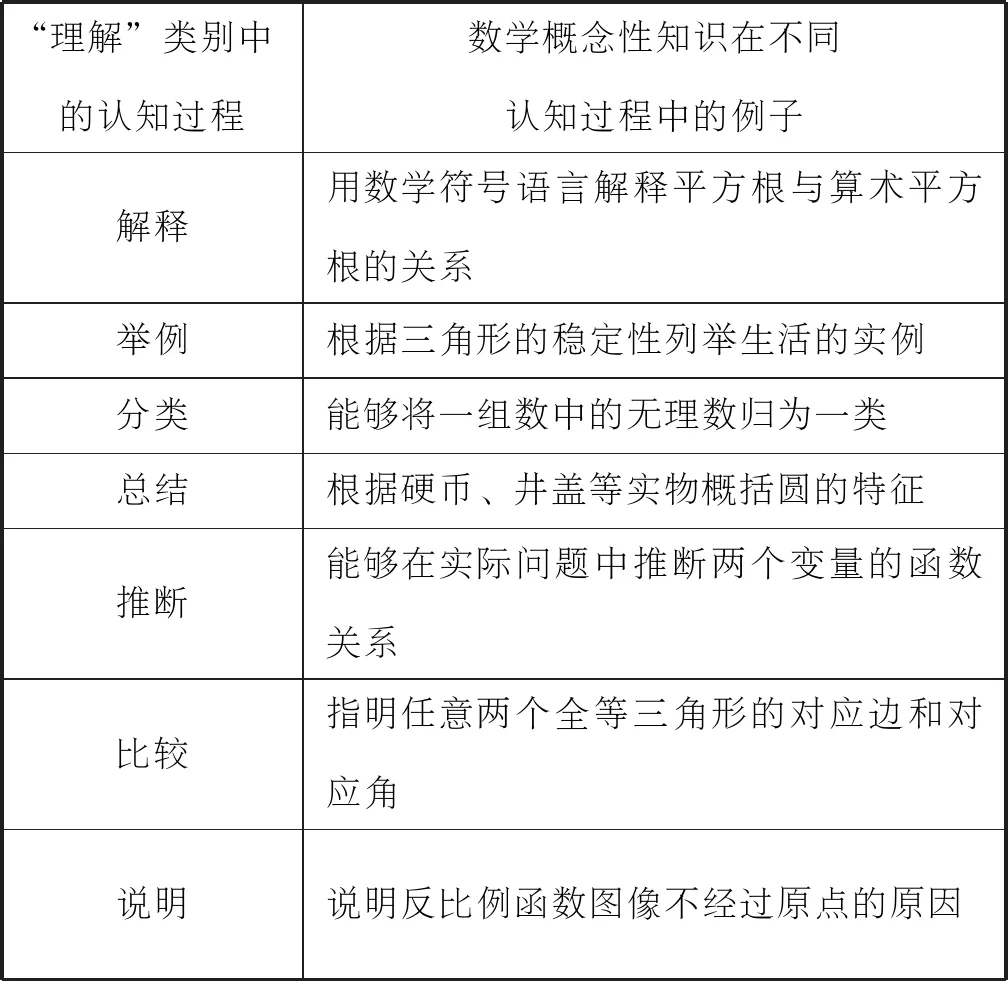
表1 数学概念性知识在不同认知过程中的例子

另一方面原因在于，不明确各认知过程在概念学习中的区别。“解释”“举例”与“分类”有利于多感官辨别大量事实的属性，是形成概念的基础。“总结”与“推断”更适合具体概念的形成，是指概括、归纳出某一类事实的本质特征，发现构成某一类事实的基本要素之间的关系。“比较”与“说明”更适合定义性概念的形成，是指发现两个对象之间的对应关系，建构某一概念体系中的因果关系。根据加涅的智慧技能层级论，形成定义性概念的前提是形成具体概念，形成具体概念的前提是辨别。因此，“比较”与“说明”是相对于“总结”与“推断”来说，更高层次的认知过程，而“解释”“举例”与“分类”是理解类别中最为基础的认知过程。实际教学中，仅用“解释”“举例”“分类”来设计教学活动和测评活动的做法都不能保证“理解”的深度。

根据广义知识学习阶段和分类模型，除语文、外语等学科的概念之外，其他学术性学科中的概念学习一般要经历陈述性学习阶段和程序性学习阶段。[18]相应地，数学概念性知识的教学需要遵循概念性知识学习的基本规律。核心素养对数学概念性知识的教学启示也应当在数学概念性知识教学的不同阶段发挥相应的作用。如在陈述性阶段实现概念的多次建构，通过概念与智慧技能的双向作用促进概念转化为对外办事的能力。此外，为了保证评价针对的是概念理解而不是概念记忆，基于“理解”类别中的不同认知过程实施数学概念性知识的测评也是十分必要的。

本文系北京教育学院2019年重点关注课题 “评价”行为对数学问题解决图式水平进阶的实验研究(ZDGZ2019-04)的研究成果。