基于“数学基本活动经验”下的教学实施——以椭圆及其标准方程为例

文∣王伯龙

一、引言

2007年4月，史宁中教授在宁波举行的数学教育高级研修班的报告中提出，要把数学教学中的“双基”发展为“四基”，即除了“数学基础知识”和“数学基本技能”之外，要加上“数学基本思想”以及“数学基本活动经验”。《义务教育数学课程标准(2011年版)》也把培养学生的“双基”转向了“四基”。《普通高中数学课程标准(2017年版)》将“四基”纳入高中数学课程目标，并强调指出，“四基”是培养学生数学学科核心素养的沃土，是发展学生数学学科核心素养的有效载体，教学中要引导学生理解基础知识，掌握基本技能，感悟数学基本思想，积累数学基本活动经验，促进学生数学学科核心素养的不断提升。

何谓数学基本活动经验？目前也没有严格的界定。张奠宙教授指出，所谓数学基本活动经验，是指在数学目标的引导下，通过对具体事物进行实际操作、考查和思考,从感性向理性飞跃时所形成的认识。郑毓信教授又指出，“数学基本活动经验是学生在积极参与数学活动的过程中，内化了的数学知识、技能与情感体验”。由此可见，数学基本活动经验是在课程目标的引导下，从数学基本活动的过程出发，通过数学归纳和演绎，尝试由特殊情形猜想一般结论，并试图验证或证明的自然思考过程，是在数学学习活动中获取的、经得起推敲的、沉积的感悟体验。

数学基本活动经验和数学基础知识不一样，基础知识是以结果的形式呈现，经验和知识的不同之处在于经验是主体经过自身实践得到的体验，知识是经历学习之后得到的结果。数学基本活动经验和基本技能不同，技能是在大量训练之后顺利完成工作任务的方式，而所有数学活动都能够让学生在学习过程中得到必要的经验。数学基本活动经验不同于数学思想，而思想本质上是方法指导，经验则是铺架在基础知识、基本技能、基本思想方法之间的桥梁。由此可见，“四基”的落实离不开数学活动，学生只有在具体的数学活动中，亲身经历观察、实践、思考、体验等过程才能有效地落实。有研究者将其关系用图1来表示。

图1

二、教学分析

以人民教育出版社出版的高中数学A版“椭圆及其标准方程”为例，利用学生已有圆的学习经验及经过观察、操作、猜想、归纳所获得的数学基本活动经验对教材“再度开发”。结合教学实际，充分考虑学生的现实水平和实际需要，挑选他们认为最合适的材料，对这些材料进行一定的处理与加工，包括适度增删、调整等；更灵活、有效地使用教材，使教学内容和教学活动最贴近学生的实际。[5]

(一)教材编写欠妥分析

“椭圆及其标准方程”一节教材编写以椭圆定义的发现—椭圆标准方程的建立—椭圆的定义、标准方程的运用为线索。其中，椭圆定义的发现环节以探究内容展开，但是我们觉得教材探究内容的设置对椭圆定义的引入有欠妥之处。

教材对椭圆定义的引入为：“把细绳的两端拉开一段距离，移动笔尖的过程中，细绳的长度保持不变，即笔尖到两个定点的距离之和等于常数。”围绕这个方法产生许多教学设计。或是让学生按教材上的叙述方法，动手画出椭圆，或是用课件演示，按定义画出椭圆，但定义是怎样想到的？两个定点从何而来？似乎是“魔术师的帽子里突然跳出一只兔子”，无法理解[6]。因此，椭圆定义产生的问题情境(探究内容)既不能充分反映数学的本质，不能体现数学逻辑性和严谨性，也不利于学生自主探究、直观理解。

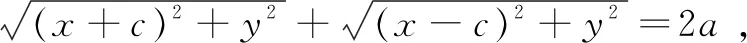
(二)重置情境，再度开发——椭圆及其标准方程的教学设计

1.重构情境，引入课题

多媒体展示图2、图3。

图2

图3

问题1：请同学们观察生活中的图2、图3，你能说出它们的大致形状吗？

问题2：大家还能举一些生活中见到的类似形状的例子吗？

设计意图：利用学生在实际生活中已获得的经验，通过生活中的图案进一步增强对椭圆形状的感性认识，使学生感受到生活中处处有椭圆。

2. 展示问题，探索定义

问题3：老师这里有一个握力器模型，你能给大家演示一下如何将它变成椭圆吗？

学生活动：(演示)挤压或拉伸，圆变成椭圆。

设计意图：借助于学生已有圆的学习经验，通过动手操作，感受椭圆是圆经过挤压或拉伸而形成的，使得学生对椭圆的认识更深入，从中获取新的活动经验：椭圆是由圆经过伸缩变换形成的。“伸缩变换”这一知识点学生在三角函数内容中已学过。

师：把一个圆均匀压缩(或拉伸)后，感觉变成了椭圆，那么它到底是不是椭圆呢？请大家探究下列问题。

问题4：如图4，在圆x2+y2=16上任取一点P，过P作x轴的垂线段PD，D为垂足。当点P在圆上运动时，线段PD的中点M的轨迹方程是什么？你能猜想出点M的轨迹是什么吗？

图4

【师生活动】求动点轨迹问题，学生在 “曲线与方程”一节中已有学习经验，求动点M的轨迹方程困难不大。经过思考，大部分学生有了结果，得出点M的轨迹方程是x2+4y2=16，但轨迹是什么图形，学生无法想象。教师用“几何画板”软件演示，让点P绕圆周运动，线段PD的中点M(设置成追踪点)所形成轨迹的形状(如图5)，让学生观察,直观感知。

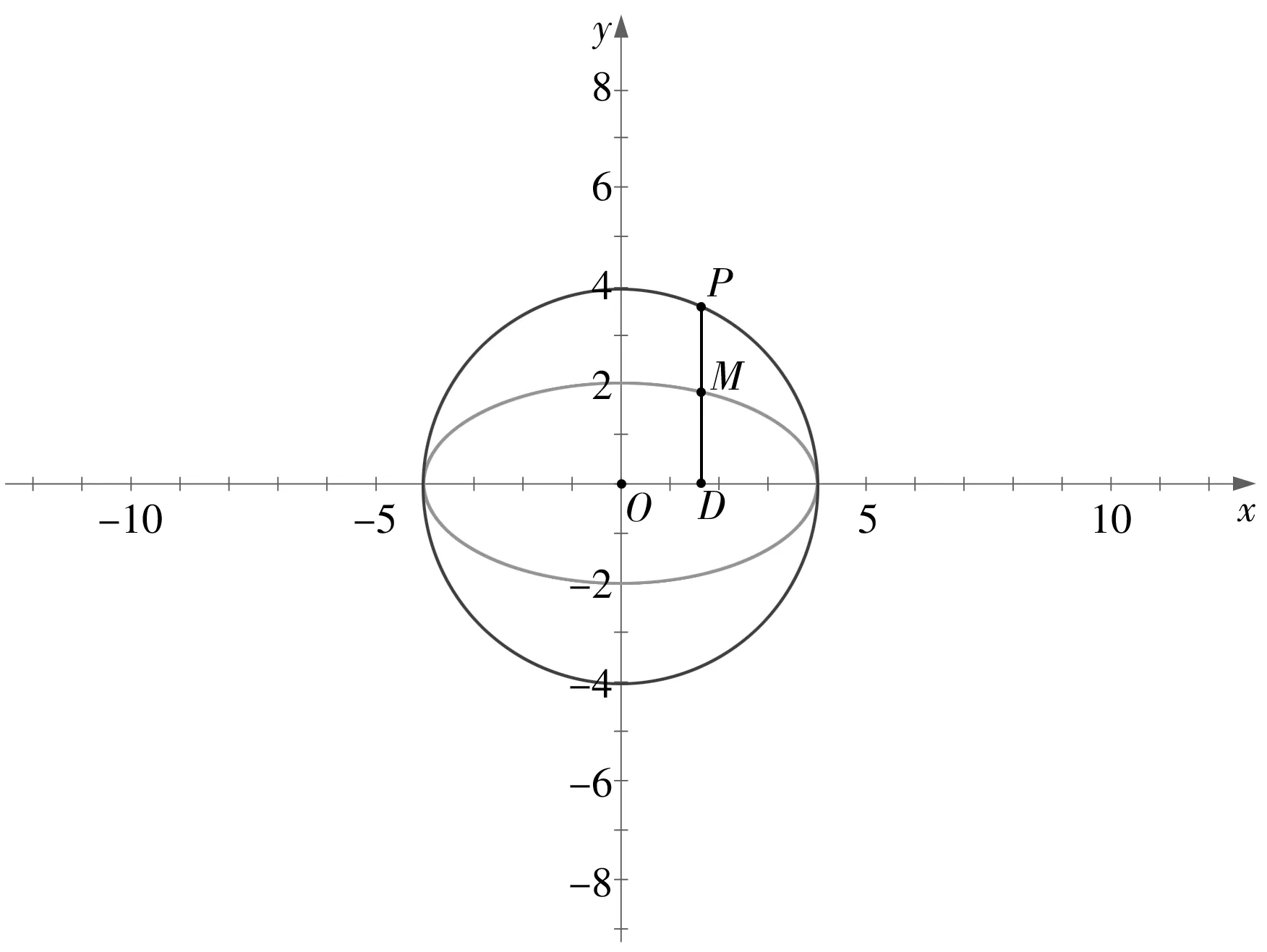
图5

师：圆的定义是平面内到一定点的距离等于定长的点的轨迹，即在圆的定义中有一个定点、一个定长。那么，椭圆能否通过定点、定长来定义？

给学生留足思考的时间，留下思考的机会，让他们思考交流、合作探究。

师追问：定义椭圆需要几个定点？有没有定长？

师生活动：部分学生猜想是两个定点。教师用“几何画板”演示，让点P沿着圆的半径PO滑到点M的过程中，圆心O沿着x轴向两边分别滑向点F1，F2(如图6)，半径PO滑到MF1，MF2的位置。

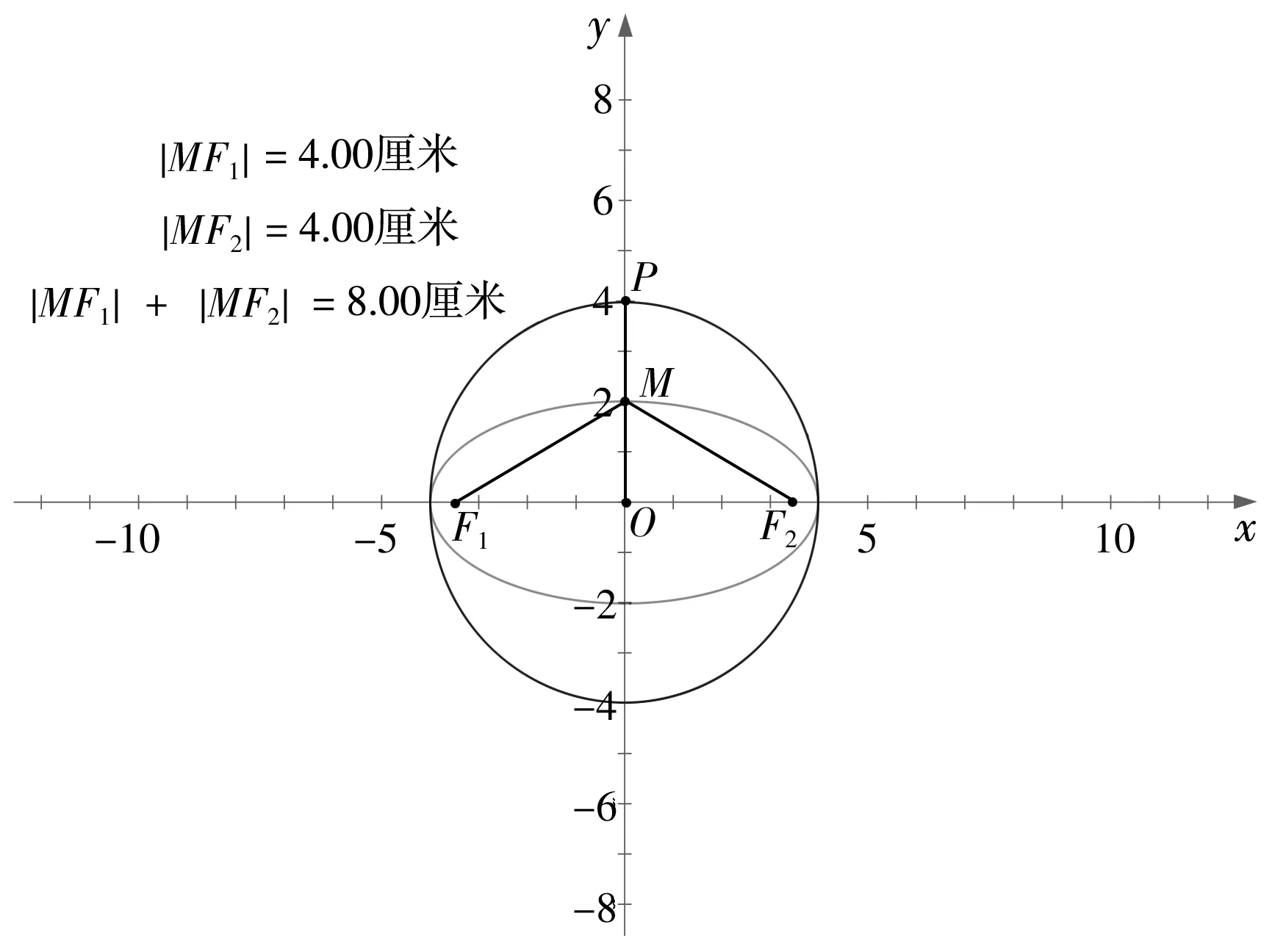
图6

问题5：请学生思考，教师刚才的演示中，有什么新发现？

教师引导学生观察演示过程，结合图形思考，观察到有两个定点F1，F2，且|MF1|+|MF2|=4×2=8(定值)。

问题6：学生发现点M在图6的位置时，有|MF1|+|MF2|=8。那么，点M在椭圆周上其他位置是否也有|MF1|+|MF2|=8(定值)呢？

教师用“几何画板”演示：让点P沿着圆周徐徐而动，同时，点M也沿着椭圆周运动，线段MF1和MF2的长度随着点M的位置的变化而改变，但始终有|MF1|+|MF2|=8。即“椭圆周上任意一点M到两个定点F1，F2的距离之和始终等于8”。让学生进行严格的论证。

设计意图：教师利用“几何画板”的演示，借助学生已有的经验，通过设置“问题串”对特例的探究，让学生经历观察、思考、交流、操作、猜想、验证等体验活动，对椭圆的形成从感性认识的层次上升到理性认识的层次，通过参与数学基本活动，获取椭圆定义初步形成的基本经验，为自主探究椭圆定义及建立标准方程储备了丰富的数学知识，掌握了基本技能，感悟了数学基本思想，积累了新的数学基本活动经验。

(三)归纳提升，形成定义

问题7：通过上面特例的探索，你能类比，从特殊到一般的归纳，给椭圆下个定义吗？

学生尝试给出椭圆的定义：平面内到两定点F1，F2的距离的和等于定长(大于两定点F1，F2间的距离)的点的轨迹叫椭圆。

教师追问：为什么要在括号内加上“大于两定点F1，F2间的距离”呢？

学生思考讨论，得出结论。如果定长等于两定点F1，F2间的距离，动点的轨迹是线段F1F2；定长小于两定点F1，F2间的距离，不成轨迹。

设计意图：让学生从特例的研究中获取数学基本活动经验。通过类比，从特殊到一般的归纳、提升、辨析，建构得到椭圆的定义，使椭圆定义的形成自然、水到渠成。同时提升学生类比和归纳的数学能力。

(四)动手实验，理解定义

问题8：老师手中有一根定长的细绳，你能利用椭圆的定义画出一个椭圆吗？

学生尝试画椭圆，先在黑板上取两个定点，再把细绳的两端固定在两个定点上，然后用粉笔拉紧细绳，移动粉笔的过程就画出一个椭圆。

设计意图：动手实验是新课程倡导的学习方法之一。学生通过动手操作，进一步理解椭圆的定义。

(五)类比特例，建立方程

师：下面我们通过上面研究特例的思想方法，尝试建立椭圆的标准方程。请大家探究下列更一般的问题。

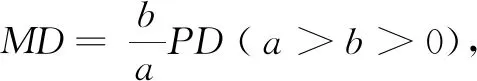
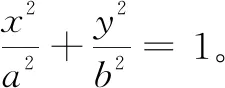
教师追问：它是椭圆的方程吗？我们如何去验证？

学生经过思考，类比研究问题5所获得的经验，只需验证方程所表示曲线上任一点M到两定点F1，F2的距离等于常数2a(大于|F1F2|)即可，即|MF1|+|MF2|=2a。这个式子的验证学生完全可以借助于研究问题6的方法和思路，轻松搞定。

教师追问：你能用同样的方法研究焦点在y轴上的椭圆标准方程吗？

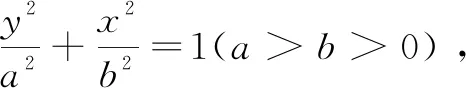
设计意图：让学生通过研究问题4和问题5所获得基本经验和已有的数学活动经验，自主探究一般情形下的轨迹方程，进一步感受椭圆是圆经过坐标压缩变换得来的，椭圆方程的建立可以经过圆方程实施坐标变换，避免了教材用两次平方化简的困惑。

(六)应用新知，提升能力

请同学们应用本节课所获得的知识，解决问题。(1)如果点M(x,y)在运动过程中，总满足关系式

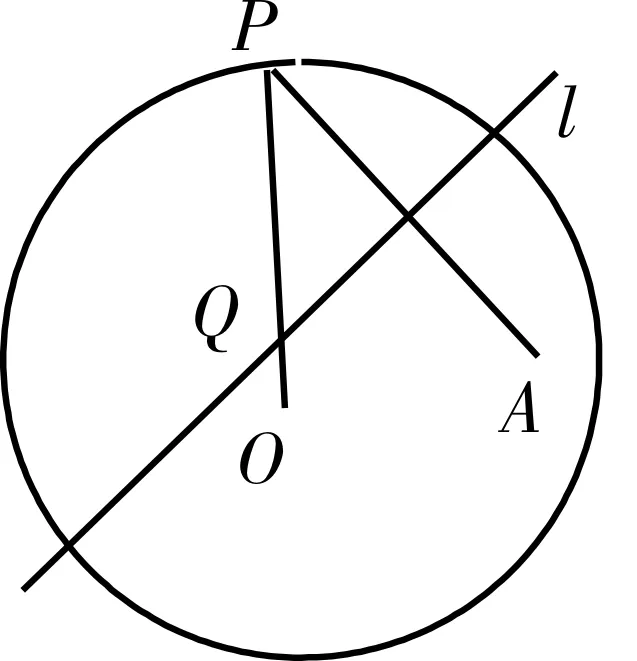
图7

设计意图：强化学生对椭圆定义及标准方程的理解，通过学生思考和练习，总结所学知识，提炼研究问题的思想方法，进一步领会研究数学概念的基本方法，让学生在学会基础知识的同时，学会研究问题的方法和技能，积累解决问题的数学经验，提升学生数学学科核心素养。

三、总结

在数学活动中，学生已有的认知经验能提升学生思维的活跃度，只有关注数学基本活动经验的获得，才能在数学教学中体现出数学的过程性，才能使学生在学习知识的过程中积累新的经验，在积累经验的过程中提炼数学思想方法。本设计改变了教材原有的编排顺序，将椭圆定义后的例题进行了改编，作为探索的主线，从学生已有圆的认知经验出发，设置合适的问题串，使学生亲身经历观察、操作、探究、猜想、验证等活动，获取新的数学基本活动经验，最后利用已获得的经验从特殊到一般，自主归纳出椭圆的定义，建立椭圆标准方程，使得新知识的呼出自然流淌。在整个教学过程中，教师的主导作用和学生的主体作用得到了充分的体现，同时，也注重数学文化的渗透，灌注了学数学就是利用活动经验做数学的理念，培养了学生的创新思维能力。

本文系宁夏第五届基础教育教学“高中数学教学中培养学生创新思维的实践研究”(JXKT-ZS-05-071)的研究成果。