渗透数学思想方法 培养数学学习能力


摘 要:为培养创造性和开拓性的人才,初中数学课堂中在开发学生智力的同时也要重视对学生数学学习能力及数学思想的培养。初一学生在数学的学习上首先应当获得能够适应中学数学学习的能力,从而让学生习惯、自然地由小学过渡到中学。文章结合教学实践经验,浅析在课堂教学中渗透数学思想方法,提高初一学生学习数学能力的实践与思考,皆在抛砖引玉。
关键词:数学思想;学习能力;初一学生
《义务教育数学课程标准》(2011年版)明确指出:“课程内容包括数学结果的形成和蕴涵的数学思想方法。”为了学生的可持续发展,提高学生数学学习能力,教师在平常的数学教学中,要有意识地渗透数学思想方法,数学思想方法是将数学知识转化为数学能力的纽带。然而学生熟练掌握数学思想方法不是一朝一夕就能形成的,初中生的数学知识还相对贫乏,抽象思维能力还有待于训练和提高,这就需要我们教师在日常教学中将数学知识作为载体,把数学思想方法逐步渗透到课堂教学中。
一、 运用数形结合思想,开发抽象思维能力
学数学既要学“数”又要学“形”。“数”与“形”既是独立的个体,又是相互联系、密不可分的统一体。当“数”与“形”相结合时,既可以使数学问题化抽象为形象,又可以让学生挖掘出问题的本质,使解题思路清晰化、明朗化,使计算过程简单化。教师在教学中若忽视“数”与“形”的任何一方面,都会使数学变得残缺不全。在初中数学的学习过程中,会涉及很多概念、公式、定理、法则等知识,这些内容相对于小学数学来说比较枯燥,而且具有较强的思辨性,这样一来很容易形成数学课堂的严肃乏味,不利于激发学生学习数学的兴趣。然而将数形结合思想引入到课堂教学中,可以改善这个问题,鼓励学生结合题目文字描述画出图像,通过文字和图像的结合理解题意,问题自然迎刃而解,不仅可以有效提高解题的效率,还可以在一定程度上开发学生的抽象思维能力。
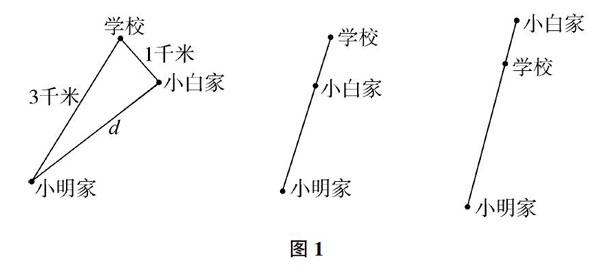
【例1】 小明家离校3千米,小白家离校1千米,记小明、小白两家的距离为d,求d的取值范围。
教学分析:这题主要考查学生如何将实际问题转化为数学问题。题目中出现了三个地点:学校、小明家、小白家,而且还知道了两两地点之间的距离。于是引导学生将这三个地点看成是三个点,三段距离看成三条线段,运用数形结合的方法,动手画图,通过三种“形”的出现(如图1),学生很快利用“三角形的三边关系”和“线段的和差”得到了正确答案为“2≤d≤4”。题目中以“数”的形式出现,有些学生连题目的意思都看不明白,通过引导学生以“形”的方式去分析问题,学生的解题思路变得很清晰,做起来也是游刃有余。
二、 学用分类讨论思想,让学生的思考更全面
分类讨论思想是在面对同一个问题时,产生了多种“歧义”,出现了不同的情况,于是对这些情况一一进行讨论,从而使问题得到解决。从小学数学到初中数学,知识点的增加,题目的综合性增强,难度的提高,经常会遇到一些题目的答案并不只有唯一一个,而是需要考虑到多种的可能性,这时便要求一定要分类讨论,特别是在初二和初三的数学题目中经常会涉及。所以学生在初一时就要有意识地去学用分类讨论思想,从多种角度考虑问题,使自己的思考更全面,解题更完整。
比如在前面的例题中,有的学生通过画图,发现三条线段构成了一个三角形,利用三角形的三边关系得到了:2 【例2】 对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数。例如M{-1,2,3}=-1+2+33=43,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=_____。 教学分析:由于2,-x+3,5x这三个数中没办法直接判断哪个是最小的,它们都有可能是最小的那个数,条件不明确,因此必须分成三种情况来讨论。而其中当3+2x+1+4x-13=-x+3时,解得:x=23。但此时min{2,-x+3,5x}=2而并非min{2,-x+3,5x}=-x+3,于是x=2/3要舍去。通过对这道题的全面分析,学生在潜意识里能够接受分类讨论思想的必要性以及分类讨论结果的可行性问题。 三、 妙用转化思想,培养分析问题和解决问题能力 遇到数学问题时,如何解题是首要考虑的。其实解题就意味着转化。转?怎样转?通过什么样的方式转?化?如何化?又要化成什么样的形式?当学生弄清转化的目的和转化的方法时,那问题便不攻而破。在华师大版的初中数学七年级的教学内容中,如:有理数的减法转化为加法来计算;有理数的除法或乘方转化为乘法来计算;二元(或三元)一次方程组利用消元法转化为一元一次方程来解答;多边形的问题转化为三角形的问题……这些都是转化思想的体现。 【例3】 如图2,已知△ABC,∠A,∠B,∠C是△ABC的三个内角。 求证:∠A+∠B+∠C=180°。 证明:过点A作DE∥BC,则 ∠B=∠DAB,∠C=∠EAC, ∵∠DAB+∠BAC+∠EAC=180°, ∴∠B+∠BAC+∠C=180°。 教学分析:证明这道题的关键是要让学生理解为什么要这样作辅助线,要让学生知其所以然。主要目的是要把∠B转化为∠DAB,把∠C转化为∠EAC,因为∠DAB+∠BAC+∠EAC=180°,于是把∠B、∠BAC、∠C的和转化为∠DAB、∠BAC、∠EAC的和,這个转化主要是通过作平行线,利用平行线的性质得到的。显然还有其他不同的作平行线的方法来证明“三角形的内角和等于180°”。类似于这种转化,在证明“三角形的外角和等于360°”时,也可以通过作平行线,利用平行线的性质把三个“分开”的外角转化为三个“聚集在一起”的角正好构成一个周角360°,因此得证。 在数学教学中,不断地渗透转化思想,让学生逐渐地领会转化的思想方法,体会在解题中如何把未知转化为已知,把陌生问题转化为熟悉问题,掌握转化的思想,并能在解题中灵活运用,从而起到了举一反三的效果。 四、 巧用方程思想,提高几何问题的解题能力 《福建省初中数学学科教学与考试指导意见》中明确指出:“在几何教学中,要注意用代数方法解决几何问题。”在近几年的中考考试中,对几何题的考查难度已逐渐提升,因此提高学生对几何问题的解决能力已迫在眉睫。然而,在初一的教学中,几何问题对于刚入初中的学生来说似乎很难理解,学生常常找不到方法和思路,每次考几何的知识,大部分学生都抓瞎,不懂得从哪里入手,导致几何题的得分率很低,这让学生对几何题总是望而却步,而且这种害怕心理会一直延续到初三年。为了改变这种现状,教师在初一的教学过程中,处理几何中的某些问题时,常常需要利用已知条件或图形的构造,建立方程来寻求答案。特别是在几何的线段和角的计算中,利用等量关系建立方程或方程组求解,这是一种非常简洁、易懂的方法。因此,方程思想对于初中生解决几何问题起到了化繁为简、化难为易的作用。 【例4】 如图3,在△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,求∠C的度数。 解:由折叠可得:∠C′DB=∠CDB=74°; ∠ABE=∠EBD=∠DBC 设∠C=x°,则∠ABE=∠EBD=∠DBC=(106-x)° ∴∠ABC=3(106-x)° ∵∠A+∠ABC+∠C=180° ∴20+3(106-x)+x=180° 解得:x=79 ∴∠C=79° 教学分析:这种看似图形复杂、解题思路难找的几何题,将要求的角度设为未知数,设法把其他有关的量用含同一个未知数的代数式表示,然后把它们代入等量关系中,建立一个代数方程,最后通过解方程得到所要求的结果。巧用方程思想代替原本用逻辑推理来解决几何问题的方法,对于初一学生来说更容易接受。因此,教师在初一的几何教学中,就应当渗透方程思想,让学生在学习中学会运用方程的观点去考察问题,运用方程的思想去分析问题,这样才能有效地沟通知识间的纵横联系,才能有助于解题思路的寻找与优化。 除了数形结合思想、分类讨论思想、转化思想、方程思想,在初一的数学教学过程中还要渗透类比思想、建模思想、参数思想……这些数学思想是数学认知的精华,是数学留给人的财富。作为数学老师,我们应该重视数学思想的教学,以提高学生学习数学的能力,促进学生知识、情感能力的协调发展,实现学生的全面发展。 参考文献: [1]义务教育数学课程标准(2011年版). [2]福建省初中數学学科教学与考试指导意见(2018年版). 作者简介: 邱明让,福建省石狮市,福建省石狮市锦峰实验学校。

