基于域适应神经网络的调制方式分类方法

史蕴豪, 许 华, 单俊杰

(1.空军工程大学信息与导航学院，西安，710077; 2.93656部队,北京，101114)

通信调制识别技术对提升通信对抗效率具有十分重要的意义。通过调制识别技术可辅助确定敌军通信源类别，进而可以对敌电台威胁程度做出评估。传统的通信调制识别技术主要是基于通信信号的时频分布、瞬时幅度、相位、频率、高阶统计量、循环谱、信息熵等作为分类特征参数，例如Azzouz[1]等利用信号瞬时特征识别不同的数字信号，Swami[2]提出了将信号四阶统计量作为分类特征，文献[3]使用高阶累积量对8类调制信号进行识别，文献[4]混合多种循环谱与高阶累积量特征对信号进行分类，文献[5～6]使用信号熵特征对不同调制信号进行分类。在分类器构造方面，学者们也提出了多种分类器，Dobre等[7]提出了二元判决树分类器，龚晓洁等[8]利用支持向量机对信号手工特征进行分类,实现了多类信号调制方式识别。归根结底，通信信号的调制识别问题可以归结为模式分类问题，即根据提取的特征参数结合分类器进行的分类过程[9]。

与早期手动提取特征识别信号类别的方法不同，卷积神经网络可以通过构建多个卷积层来自动提取信号深层次的特征并对信号分类。近些年国内外许多学者在信号调制识别方面取得了不错的成果,例如Rajendran[10]等人使用深度卷积神经网络提取信号时频特征并分类识别，在衰落信道下有较高的识别率，O'Shea[11]等人使用VGG深度卷积神经网络结合ResNet残差网络将分类的调制样式数目提升到了24种并取得了不错的分类效果。Jeong[12]等人利用短时傅里叶变换生成信号时频图像，并利用深度卷积神经网络提取时频域图像特征，最终完成了对7种调制识别方式的识别，且在信噪比为-4 dB时仍有90%以上的识别率。Meng[13]等人提出了深度神经网络联合噪声估计的调制方式识别算法，该算法设计了一种特殊的网络结构，将原始信号数据和信噪比同时作为神经网络的输入，仿真结果显示该算法识别率已经非常接近理论识别率的上限。Zufan Zhang[14]等人利用卷积神经网络提取信号SPWVD时频图特征和BJD时频图特征并与大量手工特征融合对8种调制方式进行识别，在-4 dB时仍有92.5%的识别准确率。

虽然基于深度卷积神经网络的调制方式识别技术具有较高的识别率和鲁棒性，但是当测试集样本与训练集样本存在分布差异时，利用训练集样本训练出的网络模型对测试集样本的识别率则会明显降低。而在实际战场环境中，接收端收到的信号总是与训练网络模型所用信号存在一定的分布差异，此时使用预先训练好的神经网络就很难准确识别新收到的信号，因此无法满足现代战争的作战需求。

本文假设网络训练过程中存在带标签的源域训练样本和无标签的目标域测试样本，且源域样本与目标域样本存在一定分布差异。本文拟通过训练改进型深度卷积神经网络，提升无标签的目标域样本的识别性能。

1 基于域适应网络的调制识别模型

针对实际遇到的待测样本与训练样本存在分布差异的情况，本文解决该问题的核心思想是将已有的带标签信号样本结合没有标签的目标域信号样本，对域适应神经网络进行训练，通过自编码器降维技术结合域适应技术缩小源域带标签样本与目标域无标签样本的分布差异，从而达到对目标域无标签样本的分类识别。训练、测试流程见图1。

图1 训练、测试流程图

1.1 特征提取模块

在实际战场复杂信道环境下，通信信号时域特征很容易受到敌方和噪声等的干扰和影响，从而影响信号本质表征和模式类别之间的差异，不利于做出正确的判决。时频分析在处理信号方面表现出巨大的优势，它能清晰地反应信号有意调制的规律[15]。目前利用时频分析理论分析信号的方法有很多，比如小波变换，短时傅里叶变换(STFT)[16]，Wigner-Wile变换[17],Choi-Willams变换[18]等，它们在分析不同信号时各自都有自己的优势。由于本文拟识别的信号为相位瞬变信号，它们的相位随着数字信息的不同会发生瞬变，而小波变换在捕捉信号瞬变信息上具有非常好的性能，因此本文采用小波变换对信号进行时频分析。小波变换的数学定义表达式如式(1)所示:

WTf(a,τ)=〈f(t),φa,τ(t)〉=

(1)

信号经过小波变换后，其系数绝对值WTf(a,τ)在一定程度上可以表示信号的特征，因此本文将信号小波变换后的系数绝对值WTf(a,τ)绘图并在图像域进行处理。

由于需要在图像域进行分析处理，因此本文选用对图像处理能力较强的VGG16[19]网络提取图像特征。VGG16输入的是多通道图像，输入依次通过一系列的卷积层以提取图像深层次的特征，每2～3个连续的卷积层后会接1个池化层，用于减小网络参数规模防止过拟合。经过多层堆叠的卷积层和池化层后，会接入3层全连接层，最后一层全连接层输出为1 000维特征。VGG16的网络模型如图2所示。在每一块处理单元中，VGG16卷积层的卷积核大小为3×3，核的滑动步长为1。每一块处理单元后还要接一个2×2大小的池化层。VGG16中的每一个卷积层、全连接层后面均使用ReLU作为激活函数，在部分全连接层后面还应用了dropout技术用于提高网络对测试样本的泛化能力,防止网络过拟合。VGG16相比之前比较先进的网络结构例如AlexNet[20]等，识别错误率大幅降低，且其具有很强的泛化性和可拓展性，能够很便捷地迁移到其他图片数据上[21]。

图2 VGG16网络模型示意图

1.2 自编码器

自编码器是一种无监督的机器学习方法，由编码器和解码器构成，它可以实现在对高维数据压缩的同时尽可能地保留特征信息，例如Elyor[22]等人利用自编码器构建语义嵌入层实现零样本识别，文献[23]利用稀疏自编码器实现7类调制信号的识别。自编码器可通过维度小于输入层的隐藏层表达输入层，并在输出层重构输入层，从而达到数据降维的目的。

本文使用的自编码器仅包含一层隐藏层，隐藏层的维度小于输入层。自编码器的输入X是VGG16第1个全连接层后输出的4 096维特征，隐藏层S设置有100个神经元，输入层与隐藏层、隐藏层与输出层均采取全连接的方式。假设输入层到隐藏层的映射矩阵为W，隐藏层到输出层的映射矩阵为W*,W与W*是对称矩阵，即W=W*。由于期望输出层与输入层的值尽可能的相似，以此作为训练的约束条件，因此自编码器的目标函数可以表示为：

(2)

通过最小化目标函数，从而利用100维隐层向量表达4 096维特征向量，达到特征降维的目的。

1.3 域适应技术

域适应技术是迁移学习中一种常见的方法，可以利用带标签的源域数据来提升目标域模型的分类性能[24]。本文所设计的网络是一个分类识别的模型，可通过域适应的方法将源域信号特征知识迁移到目标域信号特征上，以此实现目标域信号分类性能的提升。图3为域适应过程示意图。

图3 域适应过程示意图

通过特征提取模块结合自编码器对信号特征提取之后，计算源域特征与目标域特征之间的CORAL损失。CORAL损失是一个衡量不同域之间分布距离的方法，可用于衡量2个域之间的相似性。下面描述单个特征层在2个域之间的损失定义[25]。

(3)

(4)

(5)

式中：1表示所有元素全为1的d维列向量。

输入特征的梯度可由以下链式法则求得：

(6)

(7)

通过梯度下降、反向传播便可不断优化目标函数。

1.4 识别模型

本文提出的识别模型以VGG16网络为主体，网络输入源域信号小波变换系数图像、源域标签LS和没有标签的目标域信号小波变换系数图像进行训练，从而达到识别目标域图像的目的。源域和目标域的域适应在自编码器隐层来实现，输入的源域、目标域图像首先通过VGG16网络提取第1个全连接层的4 096维特征，之后高维特征进入自编码器进行特征降维，生成100维的源域隐层特征xT、和目标域隐层特征xS，之后计算这2个隐层特征之间的CORAL损失，最终将2个特征间的分布损失和源域图像产生的分类损失组合在一起作为网络联合优化的目标。在训练过程中，带标记的源域样本用来计算分类的损失，而计算CORAL损失则需要所有输入数据参与，其中包括没有标记的目标域样本。模型的损失函数定义如下：

L(yi,y)=Lclass(yi,y)+μlCORAL+

(8)

式中：Lclass(yi,y)表示源域信号产生的分类损失，μ为CORAL损失的权重，用于控制其和分类损失的比重。

网络结构如图4所示。网络对所有的源域和目标域图像进行联合训练，分类损失优化全部网络参数，而CORAL损失仅优化第1个全连接层和隐藏层之间的参数矩阵W。通过梯度下降优化使得总的损失函数最小，从而得到最优模型。训练后的模型可直接对目标域图像进行识别分类。

图4 网络结构示意图

2 仿真实验及分析

本文实验均基于Python下的Tensorflow、Keras深度学习框架实现，硬件平台为Intel(R)Core(TM)i7-8700CPU，GPU为NVIDIA GeForce 1060Ti。实验所用信号样本均采用matlabR2016a仿真生成，使用软件中的CWT(Continous 1-D Wavelet Transform,CWT)函数对信号进行小波变换，选择其中的db4小波，生成其小波系数图并保存。

仿真生成{8QAM、16QAM、32QAM、64QAM、128QAM、256QAM、2PSK、4PSK、8PSK、2-FSK、4-FSK、8-FSK}共计12类信号，每个类别1 000个样本，共计12 000个样本。图5(a)～(c)分别表示8QAM、2PSK、2-FSK在8 dB高斯信道下的小波系数图，各图分别代表信号序列进行离散小波变变换后，其小波系数的绝对值与时延和频率的关系。

图5 信号小波系数图

2.1 不同信号间域适应分类

本节利用6类M-QAM调制方式的信号进行域适应，信噪比为8 dB，信道为高斯噪声信道。选取6种M-QAM信号中的任意3种作为源域有标签样本，其余3种作为目标域无标签样本。在对网络训练的过程中，每批(batch)将60张图片送入网络,其中源域、目标域各30张，因此在计算CORAL损失时，NS=NT=30。损失函数中设置λ=μ=1。在更新优化损失函数时采用Adam优化器进行迭代优化。对比不加入域适应直接分类、通过域适应后再分类2种实验的效果。不加入域适应分类是用源域带标签数据训练网络然后直接对目标域进行识别，域适应分类是指联合源域、目标域数据训练网络后，再对目标域样本进行分类识别。

图6为目标域样本识别正确率曲线，在上述仿真中，各个实验包含10次迭代循环，通过结果可以看出，在最开始的几轮迭代中，未加入域适应技术的网络识别率要高于域适应网络的识别率，造成这种现象的原因是一开始训练时使用域适应技术的总损失较高，但是随着迭代次数的不断增加，网络参数不断优化，加入域适应技术网络的识别率逐渐高于未加入域适应方法的网络。

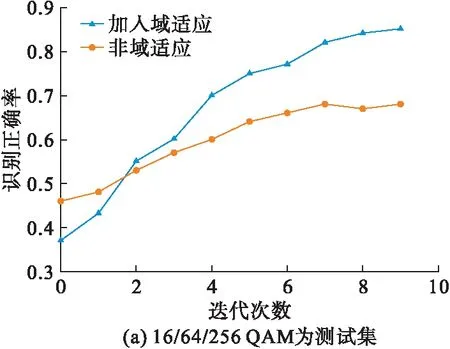
图6 目标域QAM信号识别率曲线

图7表示当测试集为8/16/128QAM时，训练过程中分类损失与CORAL损失的变化趋势，可以看出随着迭代优化2类损失之和在不断减小。

图7 Loss曲线

此外，本节使用高斯信道下信噪比为8 dB的8-QAM、32-QAM、128-QAM作为源域数据集，高斯信道下信噪比为8 dB的2PSK、4PSK、8PSK信号作为目标域数据集进行分类识别，共计50次迭代循环。如图8所示，通过M-PSK信号的分类识别实验可以看出，在网络迭代15次后，加入域适应技术的网络识别率逐渐高于没有加入域适应技术的网络。图9表示网络迭代过程中2类损失的变化趋势，可见随着网络不断迭代优化，CORAL损失、分类损失以及二者之和都在不断减小。

图8 2/4/8PSK为测试集

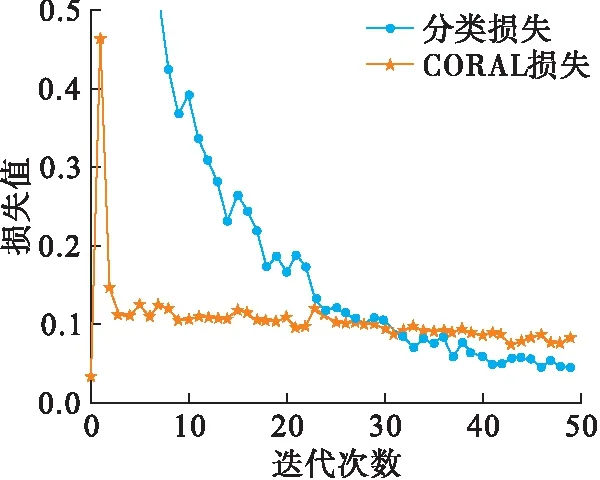
图9 Loss曲线

最后，对于不同类别信号类别间的域适应分析，使用高斯信道下信噪比为8 dB的8-QAM、32-QAM、128-QAM信号作为源域数据集，高斯信道下信噪比为8 dB的2-FSK、4-FSK、8-FSK信号作为目标域数据集进行测试，共计50次迭代。

仿真结果如图10所示，通过M-FSK信号的分类识别效果可以看出，在网络迭代50个周期后，加入域适应技术的网络识别率与未加入域适应技术的网络识别率相差不大。

图10 2/4/8FSK为测试集

2.2 不同信道下域适应分类

本节使用6类信号{8-QAM、32-QAM、128-QAM、2-FSK、4-FSK、8-FSK}在瑞利噪声信道下的小波系数图像作为目标域,利用8 dB高斯噪声信道下的这6类信号对其进行域适应训练，共计30次迭代，目标域信号识别率曲线如图11所示。

图11 瑞利信道识别率曲线

通过图11的识别率曲线可以看出，通过域适应后网络对陌生信道的识别性能有一定提升。

2.3 不同信噪比条件下域适应分类

本节使用6类信号{8-QAM、32-QAM、128-QAM、2-FSK、4-FSK、8-FSK}在0 dB高斯噪声信道下的小波系数图像作为目标域，利用这6类信号在8 dB条件下的训练样本对0 dB进行域适应训练，对比8 dB条件下的信号识别率，0 dB条件下不加入域适应技术的识别率，0 dB条件下加入域适应技术后再的识别率，实验共计30次迭代，识别率曲线如图12所示。

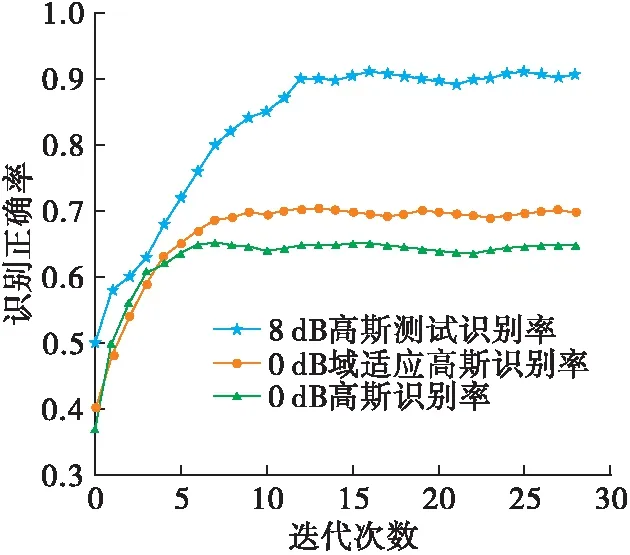
图12 不同信噪比条件识别准确率曲线

通过图12的识别率曲线可以看出，通过域适应后可提升模型在低信噪比条件下的识别性能。

对照上述实验可以得出，在本文的识别模型下，当目标域信号与源域信号特征空间相似，例如2.1中3类目标域样本与源域样本均是M-QAM信号，仅仅是调制参数不同，则通过域适应技术提升目标域信号的识别准确率效果非常明显，通过简单几次迭代便可取得不错的结果；若目标域信号与源域信号特征空间有一定差距时，例如目标域M-PSK信号与源域M-QAM信号，则通过域适应技术对目标域样本识别率的提升不明显，但随着迭代次数的不断增加，加入域适应技术识别率逐渐优于未加入域适应技术的识别率；但当目标域信号与源域信号特征空间存在明显差异，例如目标域M-FSK信号与源域M-QAM信号，则通过域适应技术对目标域样本识别率几乎没有提升。此外，通过前文分析可以看出，本文提出的域适应卷积神经网络对衰落信道下、低信噪比下信号识别性能也有一定的提升作用。

3 结语

本文针对通信调制识别中遇到的目标域测试样本与源域训练样本存在分布差异的问题，提出运用VGG16网络结合自编码器、域适应技术的识别方法，此方法利用调制信号小波变化系数图作为样本，提取出不同类别间的显著差异，并使用VGG16网络提取小波变换所得图像特征，之后通过最小化分类损失和CORAL损失之和，达到关联源域和目标域的效果。仿真结果表明，通过域适应技术确实可以提升目标域测试样本的识别率。但是，本文仍存在许多不足，例如当目标域信号与源域信号特征空间差距较大时识别率提升不明显。在今后的工作中，将尝试类间差异大的样本做域适应处理，并不断尝试新的网络模型，使网络的迁移能力达到最佳。