平尾偏转对飞机着陆滑跑性能的影响

苏光旭，张登成，魏金鹏，李海泉

(1.空军工程大学航空工程学院，西安，710038；2.沈阳飞机设计研究所，沈阳，110035)

着陆滑跑是飞机飞行的重要过程，特别是对于军用飞机而言，缩短着陆滑跑距离有利于其作战效能的发挥。国内外对着陆滑跑性能的分析做了大量研究，蔡良才等对高原机场飞机着陆滑跑距离进行计算和分析，提出了高原着陆数学模型[1]；薛宏涛等通过飞机在起降过程中的受力情况分析得到飞机起降性能的计算模型[2]；H.R.Pasindu等对湿道面飞机刹车滑跑距离建立精确数学模型，进行了试验验证[3]。在飞机着陆滑跑性能优化方面，研究多集中于改进飞机防滑刹车系统[4-5]，进而缩短着陆滑跑距离，在计算过程中也多使用现有的气动数据[6-7]，对于气动力影响的优化考虑也较少。综合以上分析，很少有针对飞机在着陆滑跑时某一气动构型计算气动数据库然后代入动力学模型进行仿真计算以优化气动力的工作先例。

因此，本文从改变飞机着陆滑跑时气动力的关键——平尾偏角入手，首先通过计算流体力学计算了不同平尾偏转工况下飞机的气动参数，对仿真计算进行数据准备，然后建立动力学模型研究了不同平尾偏转工况下飞机的着陆滑跑性能和相关参数的运动响应，并得出着陆滑跑时平尾偏转的最佳操纵方式，以期通过对飞行员的操纵指导进一步提升飞机的环境适应性。

1 飞机着陆滑跑多体动力学模型

1.1 模型假设

飞机着陆滑跑多体动力学模型基于以下假设：

1)飞机为前三点式起落架，后轮带有刹车；

2)飞机着陆对称滑跑，无侧滑，无滚转，2个后起落架受力相同；

3)后起落架完全相同，可将飞机的运动简化为铅垂面内的运动，所有作用力都在这个平面内；

4)起落架因位置锁等机械结构始终与机体保持垂直，且起落架支柱为刚性杆，无弯曲变形；

5)发动机安装角为零，且推力过重心。

1.2 坐标系定义

动力学模型所使用的坐标系定义如下：

1)地面坐标系ogxgyg固连于地面，ogxg轴平行于地面指向航向，ogyg垂直于地面竖直向上;

2)机体坐标系obxbyb固连于飞机，原点ob在飞机质心上，obxb轴位于飞机对称面内指向前方，obyb垂直于obxb指向上方。

obxb轴与地面水平线(ogxg)之间的夹角为机体俯仰角ϑ，飞机在着陆滑跑过程中航迹俯仰角θ在水平方向上变化不大，我们认为机体俯仰角ϑ即飞机迎角α。因此，α可以确定机体坐标系与地面坐标系之间的关系，坐标变换矩阵为：

(1)

1.3 多体动力学建模

采用牛顿-欧拉矢量力学方法建立飞机多体系统动力学模型[8-10]。将2个后起落架简化为1个运动体，则飞机着陆滑跑多体系统由机体B1、前起落架B2、后起落架B3以及地面组成[9]。将起落架简化为与机体相连的弹簧-油气阻尼二质量模型，将轮胎简化为与地面相连的弹簧-阻尼模型。机体运动为三自由度，即前后(航向)、上下(浮沉)以及机身俯仰；起落架运动为二自由度，即上下(缓冲器压缩)和机轮绕轮轴的转动。

图1给出了飞机着陆滑跑多体系统的受力分析。机体受到的作用力和作用力矩有升力L、气动阻力D、重力G1、发动机慢车推力Pidl、前后起落架的约束力Fyq、Fxq(Fyh、Fxh)以及气动俯仰力矩Mair，起落架受到的作用力(以后起为例)有重力G3、地面支反力Fnh、地面摩擦力Ffh、机体对其约束力Fyqb、Fxqb以及刹车力矩MT。其中除发动机推力以及机体对起落架的约束力在机体坐标系给出外，其余作用力均在地面坐标系中给出。

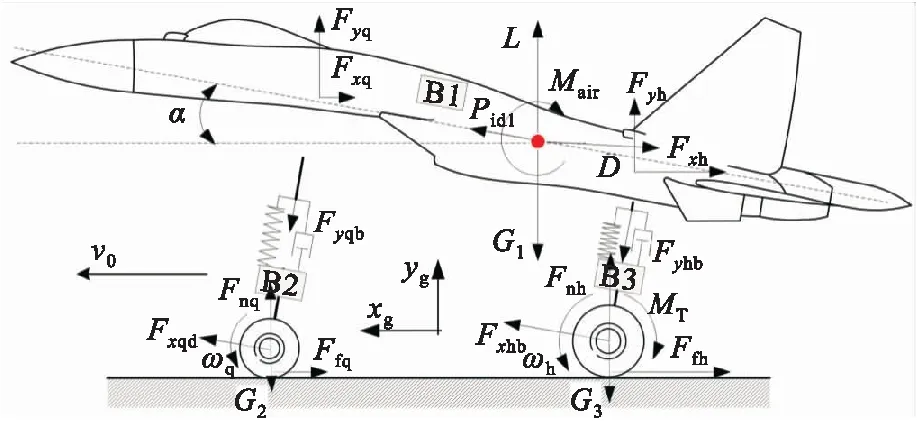
图1 飞机着陆滑跑多体系统受力分析

机体受到的约束力与起落架受到的约束力互为支反力，因此有(以前起落架为例)：

(2)

根据牛顿-欧拉方程，分别建立机体及起落架的动力学方程：

(3)

(4)

(5)

式中：Mair为机体受到的气动力矩，以抬头力矩为正；MT为后轮刹车力矩，以阻碍机轮转动为正；Rq、δq及Rh、δh分别为前轮和后轮的轮胎半径及压缩量；d1、d2的定义在下一小节给出。

1.4 多体系统运动关系

图2给出了飞机在着陆滑跑过程中机体及起落架的运动关系，其中实心点为飞机质心。起落架与机体在ogxg方向始终具有相同的速度，在某一时刻机体迎角为α，机体简化为一刚性横杆，前后起落架均简化为可压缩的作动筒，前起落架以固定铰的形式固连与地面，后起落架以转动铰的形式置于地面。其中d1、d2分别为前后起落架延长线与飞机水平参考线交点距离飞机质心的水平距离，H0为初始位置重心距离地面的高度，y为某时刻重心的在ogyg方向上的位移，yq和yh分别为前后起落架沿起落架在机体坐标系中轴向压缩行程。根据几何关系可得：

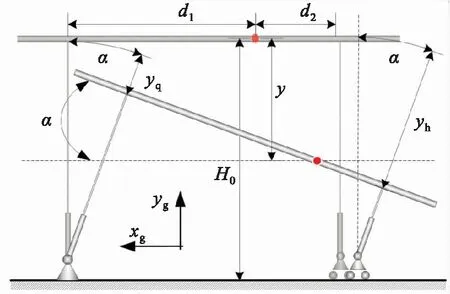
图2 飞机着陆滑跑多体系统运动关系

(6)

2 约束与载荷

2.1 气动力和气动力矩

飞机受到的气动力由以下公式计算：

(7)

(8)

(9)

式中：S为飞机机翼的投影面积；cA为机翼的平均气动弦长；ρ空气密度；v为飞机的实时速度。使用计算流体力学的方法计算机体的升力系数CL、阻力系数CD以及俯仰力矩系数Cm。

根据前后起落架的压缩行程确定飞机在着陆滑跑过程中的迎角范围，如图3所示分别计算了平尾中立δe=0°、平尾前缘上偏δe=15°以及平尾前缘下偏δe=-20°时飞机在不同迎角下的气动系数，并进行多项式拟合，为仿真计算进行数据储备，如图4所示。

图3 飞机不同的着陆滑跑迎角和平尾偏转工况

图4 不同平尾偏角下气动参数随迎角的变化规律及拟合

2.2 油气阻尼缓冲器模型

图5 起落架模型结构简化图

油液阻尼Fl主要为油液流过缓冲器油液孔时产生的阻尼力，空气弹簧力Fa为起落架缓冲器气腔内的气体压缩时产生的作用力，摩擦力Ff主要为起落架缓冲器内外套筒相对运动时产生的作用力。

(10)

其中(以后起落架为例)：

(11)

(12)

(13)

式中：P0为起落架支柱缓冲器气腔气体初始压强；V0为气腔气体初始体积；A为缓冲器上气室气压的有效面积；yh为缓冲器的压缩行程；n为气体压缩过程中的多变指数；ρo为缓冲器油液密度；ξ为油液孔的流量系数；A0为油室油孔的面积；Km、Kn为摩擦力的经验系数。气体压缩多变指数主要取决于缓冲器行程，可以根据试验数据进行拟合。

2.3 轮胎模型(以后轮为例)

在气体等温压缩的理想条件下,轮胎可用弹簧-阻尼系统[12]描述。前后落架均不考虑横向刚度的影响，轮轴与飞机在ogxg方向上具有相同的速度和加速度，轮胎受到支持力、轮轴的压力、地面摩擦力等作用力和刹车力矩。

通过轮胎载荷-压缩量经验公式可以计算轮胎在滑跑时的实时半径为：

(14)

Rh=Rh0-δh

(15)

式中：Fnh为后起落架的地面支持力；Rh0为轮胎初始半径；δh后轮压缩量；Kδ和Cδ为等效刚度系数和等效阻尼系数

轮胎的固有特性决定了Kδ和Cδ，与其能承受的最大吸收功量Wmax、最大压缩力Pmax、最大压缩量δmax等参数相关[7]，根据经验公式有：

(16)

机轮受到的摩擦力由下式计算：

Ffh=μhFnh

(17)

式中：μh为后轮与地面之间的结合系数，它主要取决于轮胎的滑移率s。

图6给出了结合系数μ随滑移率s的变化关系[13]，两者的拟合关系可由式(18)给出。

图6 结合系数随滑移率变化关系

μ=Dsin(Carctan(Bs))

(18)

式中：B、C、D均为经验参数。

轮胎的滑移率s根据定义有：

(19)

式中：wh为后轮转动的角速度。

刹车力矩MT是由机轮刹车片的相互作用产生的，它降低了机轮的滚动速度，增加了地面对轮胎表面的摩擦力，从而起到了使飞机减速的作用[19]。飞机防滑制动系统采用了速度差加压力差偏调的控制方法，经验证具有良好的制动效果[14]。

3 仿真与结果分析

3.1 模型仿真计算

使用Matlab/simulink搭建仿真模型，将机体、前后起落架缓冲器以及前后机轮分别封装为5个子系统，如图7所示。假设飞机自三点着陆时就开始使用刹车减速，滑跑初速度v0=80 m/s，初始迎角为0，飞机着陆质量为25 200 kg，采用基于Runge-Kutta法的变积分步长算法作为仿真算法[15]。

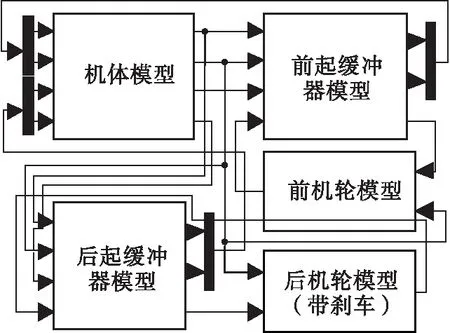
图7 仿真模型

3.2 仿真结果分析

表1给出了飞机着陆滑跑距离仿真计算结果与经过实装检验的该型飞机模拟器试验数值的对比。通过对比，仿真计算结果与试验值相近、趋势相同，相对误差保持在3%～6%之间，符合工程需求。仿真结果表明，着陆滑跑距离在平尾下偏时最小，平尾下偏滑跑距离比平尾中立滑跑距离缩短约10.7%。

表1 滑跑距离仿真计算值与试验值的对比

从图8中飞机速度随时间的变化情况可以看出在气动阻力和摩擦阻力的作用下，3种平尾偏转工况下飞机减速平缓，加速度较为稳定，符合实际情况。

图8 飞机着陆滑跑距离、速度及迎角随时间变化

图8还给出了飞机迎角随时间的变化情况，不同于平尾上偏飞机迎角一直减小的情况，平尾下偏和平尾中立时飞机迎角均为先增大后减小。平尾下偏时，飞机在2 s左右增大到滑跑状态的最大迎角并一直保持到6.7 s左右，然后开始减小到负的最小迎角，而平尾中立则是略有增加然后减小，这主要是由于3种平尾偏转工况下飞机的气动俯仰力矩的不同所导致的。

图9给出了飞机的气动力及气动力矩随时间的动态响应。由图4飞机着陆滑跑气动特性拟合曲线可知，其升力系数和气动俯仰力矩系数与迎角呈正相关，阻力系数与迎角的绝对值呈正相关，飞机的气动力和气动力矩的动态响应也反映了这一特点。由于飞机在着陆滑跑时减升增阻的措施，平尾3种工况下升力均为负值，在滑跑初始段，平尾下偏时升力绝对值最大，即对飞机机体竖直向下的作用力最大，并且3种工况下都有随迎角减小而升力绝对值增大的趋势；在气动阻力方面，随着迎角绝对值的增大，阻力系数的增大，平尾下偏及平尾中立时虽然速度不断减小但是阻力均出现了上升的趋势，在2 s左右达到峰值，平尾下偏时产生的阻力明显较大；在气动力矩方面的差异更加明显，平尾下偏产生抬头力矩，平尾上偏产生低头力矩，平尾中立时气动力矩作用效果较小，这也是不同平尾偏转工况下迎角变化差异的主要原因。3种工况下气动力矩均随速度减小而减小致零。

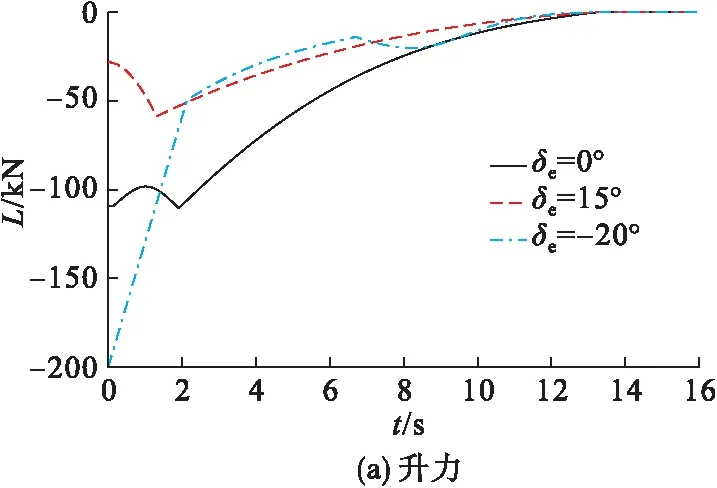
图9 飞机气动力及气动力矩随时间变化

图10给出了不同平尾偏转工况下飞机后起落架的压缩行程以及地面支反力的动态响应情况。

图10 飞机后起落架压缩量及地面支反力随时间变化

可以看出，飞机在着陆滑跑时后起落架缓冲器迅速压缩，压缩量在平尾下偏及平尾中立时达到最大，而且在平尾下偏时最大压缩量保持到4 s左右，之后随着负升力的不断减小，后起落架的压缩量波动减小。后起落架的地面支反力与起落架压缩量变化趋势基本相同，均在着陆压缩的瞬间产生了峰值。通过以上分析可得，平尾下偏时后起落架的压缩量较大，地面支反力较大，产生的机轮摩擦阻力也更大，减速效果更好。

4 结语

本文根据多体运动关系建立了飞机着陆滑跑动力学模型，通过数值模拟计算得到气动数据库，并进行了仿真计算，具体结论有：

1)本文的仿真结果同经过实装验证的飞行器模拟器仿真结果进行对比，证明本文所建立的动力学模型以及对多体运动关系的简化能够较为准确地描述飞机地面制动时的动力学特性；

2)通过对计算结果的分析，发现平尾下偏时产生的减速效果较好，能够有效缩短飞机着陆时的地面滑跑距离，对于该型飞机以及其他具有常规气动布局的飞机在着陆滑跑时平尾的操纵策略都具有一定的指导意义。