基于二维尺度维纳后滤波器的SFCW MIMO雷达成像伪影抑制方法

蒲 涛, 童宁宁

(空军工程大学防空反导学院，西安，710051)

基于步进频连续波(Stepped Frequency Continuous Wave, SFCW)的MIMO雷达在多个领域中均有广泛的应用，如穿墙人体检测、位移监测和地下物质检测等[1-3]。其中，二维成像是实现所需功能的重要信号处理步骤之一。传统上，通常使用后向投影方法(Back Projection, BP)来进行成像[4]。然而，BP方法重构的目标图像存在许多伪影，给后续的目标检测或者干涉测量等工作带来了不利影响。

现有伪影抑制方法有很多，如窗函数法[3]、互相关法[5]和CLEAN法等[6]。近年来，基于相干因子(Coherence Factor, CF)及其变体(如广义CF、符号CF和相位CF等)的伪影抑制方法得到了广泛的研究[7-9]。CF的定义为给定信号的相干功率与其非相干功率的比值。文献[10]证明了基于CF的伪影抑制方法等价于DAS无失真波束形成器的全尺度维纳后滤波器，同时，文献[10]提出，可根据实际应用情况，选择不同的尺度因子，在鲁棒性较好的维纳后滤波器和鲁棒性较差的CF方法之间做出权衡。然而，成像伪影通常也由SFCW信号的有限带宽和MIMO雷达的系统函数造成，这在大多数现有的基于CF的伪影抑制方法中并没有得到考虑。因此，大多数方法实际上只能抑制由有限孔径长度上所有空间采样点相干叠加引起的一维方位向伪影。

对于SFCW MIMO雷达，频域BP成像方法实际可以看作一个二维无失真波束形成器。因此，为了同时消除有限孔径和有限带宽所造成的二维伪影，本文将一维尺度维纳后滤波器扩展到二维情况。文献[11]提出了一种基于二维扩展CF(Extended CF, ECF)的伪影抑制方法，这种方法可以看作是所提出方法的全尺度版本。在多目标情况下，基于ECF的伪影抑制方法会低估目标的反射系数，使弱目标无法得到检测。对于所提出的方法，通过选择适当的尺度因子，可以在一定程度上克服这些局限性，很好地抑制伪影。另外，本文还讨论并通过仿真结果验证了尺度因子对最终成像性能的影响。

1 信号模型和BP成像方法

1.1 SFCW MIMO雷达

图1为M发N收的SFCW MIMO雷达的几何结构，其中，第m个发射阵元坐标为(xm,0)，第n个接收阵元坐标为(xn,0)。假设一点目标位于(x0,y0),则其到第l对接收机和发射机(即第l个空间采样点)的平均距离可以表示为：

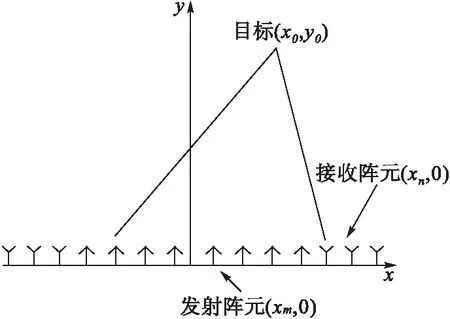
图1 SFCW MIMO雷达几何结构

(1)

式中：l=(m-1)N+n=1,2,…,MN。

假设成像区域被划分为I×J个网格点，其中x轴被划分为I个网格，y轴被划分为J个网格，而且目标分别位于特定的网格点上，则对于第q个频率和第l个空间采样点，解调后的接收信号可以表示为：

S(l,q)=

(2)

式中：fq=f0+(q-1)Δf，f0为起始频率，Δf为频率间隔；Rl(xi,yj)表示位于(xi,yj)处的目标对应第l个空间采样点的距离；σ(xi,yj)为目标反射系数；c是光速；n(l,q)是噪声。

1.2 BP成像方法

频域后向投影(Frequency Domain Back Projection, FDBP)方法是SFCW雷达的典型成像方法之一，其通过对所有空间采样点和所有频率的接收信号进行相干叠加，得到目标的反射系数。基于FDBP和接收信号S(l,q)，位于(xi,yj)点处的目标的反射系数可以由式(3)估计得出：

σFDBP(xi,yj)=

(3)

式中：Q为总的步进频数。

在实际应用中，为减少运算量，常使用时域后向投影(Time Domain Back Projection, TDBP)方法[12]来代替FDBP进行成像。基于TDBP方法，目标反射系数可以由下式估计得到：

(4)

式中：

(5)

是第l个空间采样点对应的时域距离压缩信号，可通过快速傅里叶逆变换得到。

1.3 伪影及其产生原因

虽然BP成像方法简单易行，但其成像结果具有较强的伪影。强伪影使得弱目标不易检测，且多目标的伪影会产生假峰，对后续处理造成负面影响。产生伪影的一个原因是SFCW信号的有限带宽。一般来说，每个空间采样点对应的时域距离压缩信号是一个类sinc函数。强目标在一定距离内的旁瓣会在其近距离内产生伪影。此外，雷达的系统函数也可能对距离压缩造成影响，从而产生比类sinc函数更高的旁瓣电平。

即使在理想距离压缩的情况下，在对所有空间采样点的距离压缩信号做相干求和的过程中仍会产生伪影。如图2所示，对于实际没有目标的成像点，其双曲线与目标双曲线的交点将使该成像点具有非零值。如果孔径尺寸变大，伪影水平会相对降低。因此，可以将这种伪影视为由有限的孔径长度引起的。

图2 所有空间采样点相干叠加造成的伪影

2 基于二维尺度维纳后滤波器的伪影抑制

2.1 二维尺度维纳后滤波器

重新考虑基于式(3)的FDBP成像方法，定义成像点(xi,yj)处经过相位补偿的接收信号为：

S(xi,yj)=[S(1,1)e+j4πf1R1(xi,yj)/c,…,

S(MN,Q)e+j4πfQRMN(xi,yj)/c]T

(6)

此时，式(3)可以被重写为：

σFDBP(xi,yj)=WHS(xi,yj)

(7)

此外，式(2)中S(xi,yj)可由下式给出：

S(xi,yj)=σ(xi,yj)1+P

(8)

式中：1是MNQ×1的全1向量；P是包含目标和噪声的非期望向量。因此，当使用均匀加权二维无失真波束形成器时，可以得到：

σFDBP(xi,yj)=σ(xi,yj)+WHP

(9)

从式(9)可以看出WHP是产生伪影的根本原因。因此，需要进一步处理来降低WHP的影响。

对于任意给定的无失真波束形成器，即WH1=1，维纳后滤波器可以用来最小化估计值的均方误差[9]，即：

Hwiener=

(10)

式(10)中Hwiener的估计结果为：

Hwiener=

(11)

式中：R为S(xi,yj)的协方差矩阵；Rp为非期望向量P的协方差矩阵。通过Hwiener，位于(xi,yj)处目标的反射系数可以被估计为：

σwiener(xi,yj)=HwienerWHS(xi,yj)

(12)

在式(11)中，σ(xi,yj)和Rp是未知的，需要进行估计得到。当P中仅包含噪声时，可以用σFDBP(xi,yj)作为σ(xi,yj)的估计值，并且通过下式计算WHRpW：

WHRpW=

(13)

然而，除了噪声，P中还包含有来自其他目标的非期望值。因此，上述估计方法并不恰当，会导致伪影抑制效果不佳。考虑到基于CF的方法在点目标一维伪影抑制中取得的良好效果，对式(11)进行修改，可以得到二维尺度维纳后滤波器，表示为：

Hwiener=

(14)

式中：β为尺度因子；σ(xi,yj)和WHRpW分别由式(7)和式(13)估计得到。

2.2 对比分析

2.2.1 与一维CF方法的关系

重新考虑式(4)给出的TDBP方法，成像点(xi,yj)的时域信号可表示为：

St(xi,yj)=

[St(1,2R1(xi,yj)/c),…,St(MN,2RMN(xi,yj)/c)]

(15)

因此，式(4)可以被重写为

(16)

基于CF的方法[6]利用相干因子乘以由TDBP方法的所得结果来降低由有限孔径长度造成的伪影。此时，(xi,yj)处点目标的反射系数可以表示为：

(17)

式中，

(18)

(19)

比较式(18)和式(14)，可以看出，在一维情况下，基于CF的方法可以看作全尺度维纳后滤波器，即尺度因子β=MN。然而，基于CF的伪影抑制方法仅考虑了由有限孔径长度上所有空间采样点相干叠加时引起的伪影，忽略了由有限带宽引起的伪影，从而这类伪影仍然存在。

2.2.2 与二维ECF方法的关系

在文献[10]中，基于CF的伪影抑制方法被扩展到超宽带雷达的情况。ECF被定义为来自所有频率和空间采样点的信号的总相干功率与总非相干功率之比，此时，(xi,yj)点目标的反射系数可以表示为：

σECF(xi,yj)=ECF(xi,yj)·WHS(xi,yj)

(20)

式中：

ECF(xi,yj)=

(21)

(22)

与式(14)相比，基于ECF的伪影抑制方法显然是所提出方法的全尺度情况，即在尺度因子β=MNQ时，基于ECF的伪影抑制方法与所提出方法相同。尽管基于ECF的方法可以获得比基于CF的方法更好的伪影抑制性能，但是，仿真结果表明，ECF方法会低估目标的反射系数，从而使得弱目标无法得到检测。

2.2.3 尺度因子的作用

本文所提出的尺度维纳后滤波器设有尺度因子β，其范围为从0到MNQ的整数。当β=0时，Hwiener=1。此时，BP成像方法产生的伪影不会得到抑制。当β=1时，尺度维纳后滤波器将降级为标准维纳后滤波器。由于式(13)不能很好地估计P的功率，仅有部分成像伪影会得到抑制。当β=MNQ时，尺度维纳后滤波器会转变为基于ECF的伪影抑制方法。因此，应当在鲁棒性较好的标准维纳滤波器和鲁棒性较差的ECF方法之间做好权衡来选择尺度因子β。在后面的仿真部分，本文分析了不同情况下伪影抑制性能和鲁棒性之间的关系。

3 仿真验证

为了评估所提出的伪影抑制方法的性能，本文进行了仿真试验，仿真参数见表1，MIMO雷达的阵列结构如图3所示。发射信号从4 GHz到8 GHz以约3.9 MHz的频率步进，步进频数为1 024，为了减少运算量且与分辨率相当，网格数设置为41。

表1 仿真参数

图3 MIMO雷达的阵列结构

为模拟实际情况，在接收信号中加入高斯白噪声，信噪比为10 dB。图4给出了不同方法对位于(0, 2)处的点目标的成像结果。如图4(a)所示，由于有限的带宽和有限的孔径长度，FDBP方法产生了许多强伪影。基于CF的方法可以获得较好的伪影抑制效果，如图4(b)所示。然而，由于其仅能对有限孔径长度产生的伪影进行抑制，仍然存在由有限带宽引起的强伪影。对于尺度因子β= 1的所提方法，由于式(13)低估了非期望信号的功率，因此伪影不能得到很好的抑制；与图4(a)所示相比，仅抑制了由加性噪声引起的伪影，如图4(c)所示。当尺度因子β= 65 536时，所提出的方法与基于ECF的伪影抑制方法相同，距离向和方位向的伪影均得到很好的抑制，如图4(d)所示，在60 dB的动态范围内，没有残留伪影。

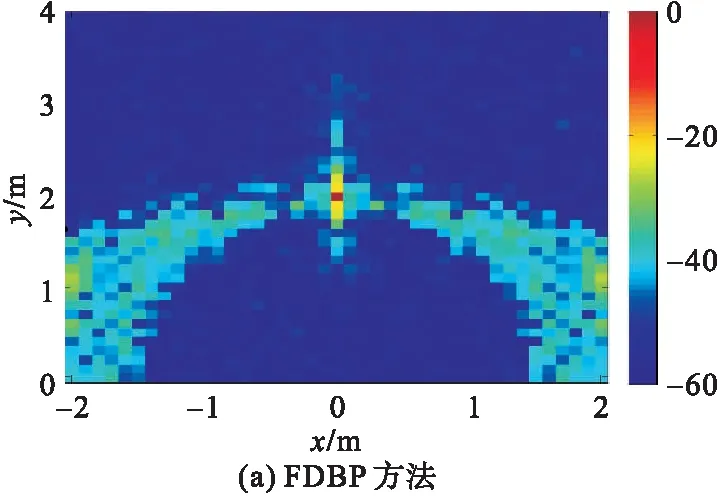
图4 不同方法对点目标的成像结果

但是，随着尺度因子的增大，非期望信号的功率也会增大。如上所述，当尺度因子β= 65 536时，所提出的尺度维纳后滤波器，即基于ECF的伪影抑制方法，会低估目标的反射系数，使弱目标无法得到有效检测。为了证明这个现象，当尺度因子β= 1和β= 65 536时，利用所提方法对反射系数幅度比为1∶1.5∶2且分别位于(1, 2)，(0, 2)和(-1, 2)的3个目标进行成像的结果如图5所示。从图5(a)可以看出，当尺度因子β= 1时，虽然残留了一些伪影，但这3个目标反射系数的幅度比得到了比较理想的估计。然而，从图5(b)可以看出，伪影抑制的代价是对目标反射系数的错误估计，3个目标反射系数均被不同程度的低估，在(-1, 2)处反射系数较低的目标几乎是不可检测的，而(0, 2)处的目标反射系数也被大幅低估，可以看出，较大的β值会导致反射系数的错误估计，尤其是对弱目标的影响更大，甚至淹没弱目标。因此，应在不同实际成像应用的情况下在伪影抑制性能和鲁棒性之间进行良好的权衡。

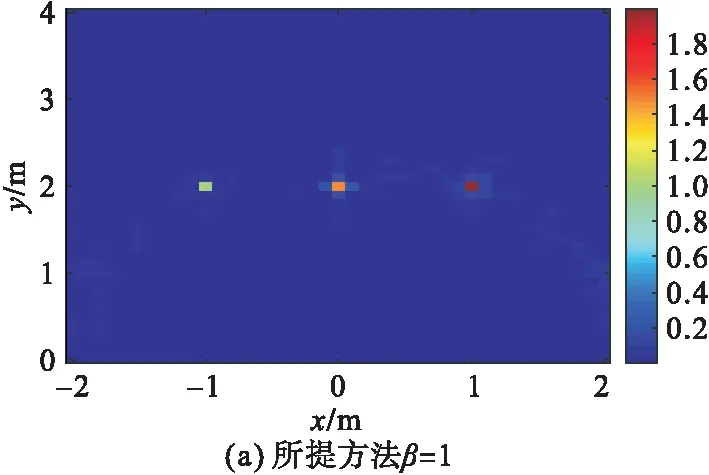
图5 不同β值时两个目标的成像结果

为了显示尺度因子β对成像结果的影响，我们在一个目标的情况下，计算了不同β值下的最大成像旁瓣电平；同时，在两个目标的情况下，计算了不同β值下两目标反射系数估计的幅度比，结果如图6所示。可以看出，随着尺度因子β的增加，旁瓣电平将逐渐降低，而幅度比将逐渐增加。在图6中，黑色垂直线表示β= 2 048，在这种情况下，旁瓣幅度降低到大约-40 dB并且两目标幅度比变化不大。因此，在实际中可以利用β= 2 048来平衡伪影抑制性能和鲁棒性。

图6 最大旁瓣和目标幅度比与尺度因子β的关系

4 结语

通过将传统的FDBP成像方法转化为二维无失真波束形成器，本文采用尺度维纳后滤波器来抑制由有限带宽和有限孔径引起的成像伪影。基于CF的方法和基于ECF的方法分别是所提方法的特例。通过仿真分析和验证了尺度因子对最终成像性能的影响。与基于CF的方法相比，所提方法能更有效地抑制伪影。通过选择合适的尺度因子，所提方法比基于ECF的方法更适合于多目标情况。在实际应用中，如何更好地自适应选择尺度因子需要进一步研究。