基于微分流形理论的结冰条件下飞机鲁棒动力学边界研究

李颖晖, 桂业伟, 左仁伟, 董泽洪, 张久星

(1.空军工程大学航空工程学院，西安，710038；2.中国空气动力研究与发展中心空气动力学国家重点实验室，四川绵阳，621000；3.93756部队，天津，300131)

飞机结冰是过冷水滴(温度低于冰点的液态水)撞击机体表面并发生相变的一种复杂现象[1-3]。结冰能够破坏飞机的气动特性，降低飞机的操稳性能，对飞行安全造成严重威胁[4-6]。尽管国内外学界针对飞机结冰的研究已经持续了数十年，期间发展出多种防/除冰技术[7-8]，但由于国内外航班数量显著增长，结冰引发的飞行事故屡屡发生：据美国运输安全委员会(NTSB)统计，1978—2005年间结冰共造成645起飞行事故[9]，同时期美国航空航天局(NASA)报道了299起结冰引发的飞行事故。随后在2006—2010年间，NTSB和NASA报道了228起结冰相关的飞行事故[10]。

由于飞机承载能力和负荷的限制，部分型号尚未装备防除冰系统。此外，由于最大载荷的限制，部分装备防除冰系统的飞机也不能将机翼表面的积冰完全除尽，且积冰融成的液态水在机翼后缘易再次凝结。为实现飞机带冰安全飞行，带冰飞行已成为当前亟待解决的课题。要解决飞机带冰飞行的安全问题，首先需要掌握结冰对飞机飞行性能的影响机理。鉴于此，国外学者主要采取飞行试验[11]、风洞试验[12]和数值模拟[13]3种方式进行研究，并且已经在飞机结冰试验设备、研究软件等方面取得了显著进展，形成了大量试验数据和经验规律。2000年，NASA在关于飞机结冰的报告中详细分析了结冰对飞机气动特性的影响[14]，2001年，Bragg团队提出了能够反映不同结冰程度下气动参数变化的结冰因子影响模型[15-16]。近年来，国内学者提出了飞机结冰的多重安全边界的概念，并指出飞机结冰防护系统应依据结冰致灾链路中各环节的边界对应的防护需求进行设计[17]。在此基础上，学者们进一步提出一系列结冰条件下飞机安全边界保护方法，主要涵盖结冰条件下飞机风险评估、参数辨识和控制律设计等问题[18-25]。然而，上述研究均依赖于精准的飞机结冰模型，未考虑到带冰飞机飞行环境的多变性和复杂性，由于实际飞行中很难获取精确的冰型信息和结冰程度，因此亟需开展针对动力学边界的鲁棒性研究。

1 流形理论及结冰条件下飞机动力学模型

1.1 流形理论

流形理论是一种计算非线性系统稳定域的有效方法,其利用积分的方式获取边界上不稳定平衡点的稳定流形并将其作为稳定边界[20]。计算二维流形的方法主要包括连续边值问题法、测地圆法、偏微分方程法和扩展轨线法[26]。本文采用测地圆法刻画系统的流形，具体流程见图1。

图1 测地圆法刻画二维流形

1.2 纵向动力学模型

本文采用如下的飞机纵向通道动力学模型：

(4)

式中：

(5)

GTM飞机采用放宽稳定性技术，为提高稳定性，设计增稳控制律见式(6)，增稳补偿控制器结构框图如图2所示。

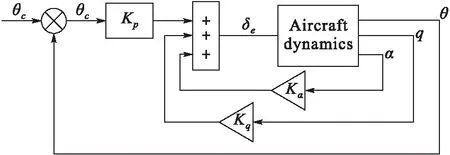
图2 增稳补偿控制器结构框图

δe=kαΔα+kqΔq

(6)

式中：δe为升降舵偏角；α0、q0分别是配平点处的迎角和俯仰角速度；Δα=α-α0和Δq=q-q0为状态变化量；控制系数取kα=1、kq=0.01。

以H=4 000 m、V=162.25 m/s为飞机状态，证明以上方法的准确性。本文研究的配平点处飞行状态信息具体如下：

(7)

式中：δth为推力系数。

1.3 结冰模型

本文采用Bragg团队于2000年提出的飞机结冰模型[15-16]，该模型初步解决了结冰气动数据的获取问题，具体表达式如下：

CA,iced=(1+ηfice)CA

(8)

式中：CA和CA,iced分别是结冰前、后飞机气动导数值；fice是结冰系数，反映CA对结冰的敏感性，对于给定的飞机为常值，不同气动系数对应的fice不同；0≤η<1是结冰因子，结冰程度越严重，η越大。结冰因子体现在飞机的气动参数模型中，对于纵向通道，主要影响飞机的升、阻力系数和俯仰力矩系数，结冰程度越严重，结冰因子的值越大，升力系数和俯仰力矩系数下降越多，阻力系数增加越多。

图3 结冰前后升力系数曲线变化示意图

2 动力学的确定及准确性验证

2.1 动力学的确定

为了详细说明基于微分流形理论计算飞机动力学边界的过程，首先计算该状态下所有的稳定平衡点(Stable Equilibrium Point，SEP)和不稳定平衡点(Unstable Equilibrium Point，UEP)，如表1所示。

飞机的动力学边界时由SEP稳定边界上所有UEPs的流形组合而成，在求出所有的平衡点后需要验证这些平衡点是否处于稳定边界上。简单的方法是在UEP处施加一个指向SEP的小扰动，这样以来，UEP点处不稳定的平衡状态被破坏，如果状态最终能够收敛至SEP，则该UEP处于稳定边界上，反之不然[29]。将表1中的所有Ⅰ型UEP代入上述流程，结果如图4所示。

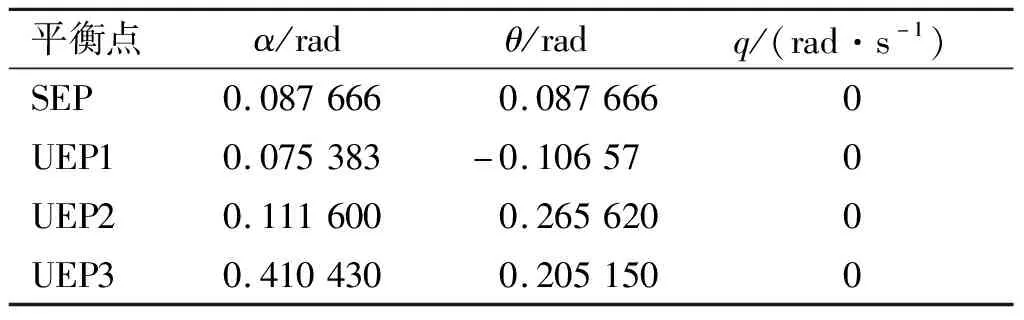
表1 所有平衡点

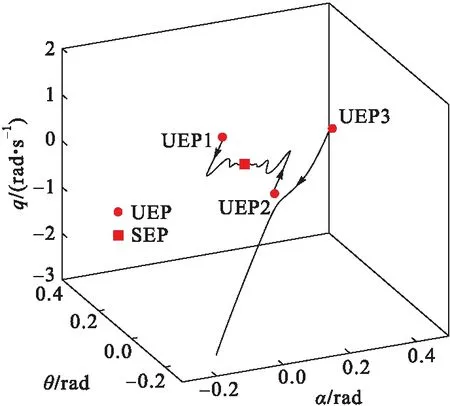
图4 确定稳定边界上的UEPs

UEP1和UEP2在受到扰动后收敛至平衡点SEP，而UEP3受扰动后呈发散趋势，因此UEP1和UEP2在稳定边界上，UEP3不在SEP的稳定边界上。由微分流形理论确定系统稳定域的方法具体如下：首先要确定SEP边界上所有的UEP，然后计算每个UEP的稳定流形，将这些流形组合起来即围成非线性系统的稳定域。本例中，UEP1和UEP2的稳定流形包围的区域即为GTM飞机在所给工作状态的三维纵向稳定域，如图5所示。

图5 微分流形法得到的稳定域

图5中红点表示SEP，蓝点表示UEP，紫色曲面表示动力学边界，紫色曲面围成的区域即为稳定域。可见飞机的稳定域并不是规则的几何形状，在计算维度超过二维后难于使用解析方法(如Lyapunov能量函数法)得到准确的稳定域。

2.2 动力学边界的准确性验证

由于飞机的纵向三维稳定域不是规则的几何形状且难于使用解析方法进行验证，本文采用动力学仿真法进行准确性验证。Monte Carlo法可在选取范围内以一定的间隔取不同初始状态，力图遍历范围内所有状态点，通过大量动力学仿真，最终收敛至SEP的即为动力学边界内的状态点(简称内点)，所有内点的集合即为稳定域内的状态点，从而可以得到飞机的动力学边界。因Monte Carlo法的理论具备基础性和广泛性，通常被用作复杂理论的验证。本文为了验证基于微分流形理论所得稳定域的准确性，采用Monte Carlo法对其进行验证，网格的划分以及范围的选取如表2所示。

表2 基于Monte Carlo法的状态范围及网格划分

值得注意的是，Monte Carlo法虽然理论简单易懂，但其计算效率低，计算耗时长，而飞机动力学特性复杂，且动力学因素间耦合性强，加大了计算的复杂度，为了说明微分流形法在计算效率上的优越性，利用微分流形法和Monte Carlo法在Intel(R)Core(TM)i7-4690 CPU、主频3.6 GHz、8 GB内存的台式机上进行相同工况的动力学边界仿真计算，使用微分流形法用时1.34 min，而使用Monte Carlo法用时124 min，可说明微分流形法具有较高的计算效率。基于Monte Carlo法得到的动力学边界验证结果如图6所示。

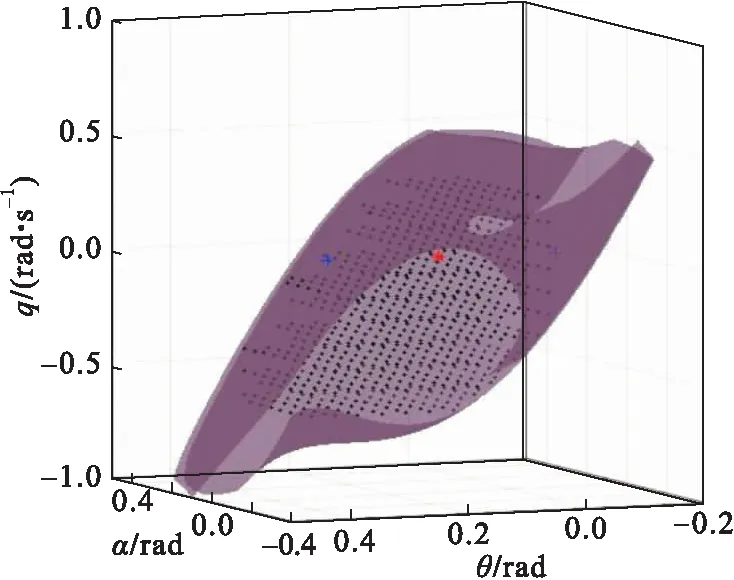
图6 微分流形法和Monte Carlo法的稳定域对比

图6中黑点构成的区域代表利用Monte Carlo法得到的稳定域，紫色曲面围成的区域代表利用微分流形法得到的稳定域。从图中可以看出，2种方法得到的稳定域吻合，验证了微分流形法所得稳定域的准确性。同时其具备较高的计算效率，且能处理动力学因素耦合的复杂情形，因此在计算飞机动力学边界时具有独特优势。

3 飞机的鲁棒动力学边界

3.1 结冰条件下飞机动力学边界

结冰会导致在相同迎角下飞机的升力下降，受到的阻力增加，舵效降低。为了维持飞机飞行所必须的升力，结冰条件下飞机必须通过增大迎角来获得足够的升力，而迎角的增加势必造成阻力的增加，此时飞机容易进入失速状态。为保证飞行安全，必须在飞机陷入失速前及时的纠正飞机的状态，因此构建一个准确的结冰动力学边界对于保障结冰条件下飞机的飞行安全具有关键作用。

以H=4 000 m、V=162.25 m/s、α=0.087 7 rad、θ=0.087 7 rad、q=0 rad/s为研究状态，考虑结冰程度η=0.2和η=0.3的情形，结冰条件下飞机的动力学边界如图7所示。

图7中绿色曲面为干净飞机，反映未结冰情况；蓝色曲面为结冰因子η=0.2时的动力学边界，反映轻度结冰情况；橘色曲面为结冰因子η=0.3时的动力学边界，反映中度结冰情况。绿点、蓝点和橘点分别表示干净飞机、结冰因子η=0.2和η=0.3的配平点。可见随着结冰程度的加剧，由于气动性能下降，飞机需要更大的配平迎角以提供足够的升力。同时，由图7可知，飞机的动力学边界随着结冰程度的加剧不断收缩。

3.2 动力学边界的鲁棒性研究

在飞机飞行过程中，由于飞行环境持续变化，飞机的气动参数存在诸多不确定性。且当飞机结冰条件下机体表面的冰在不断累积，以目前的技术手段难以获取准确的冰型信息和结冰程度，因此，对于结冰条件下飞机动力学边界的鲁棒性研究相当重要且迫切。

为了使求得的动力学边界具有鲁棒性，定义鲁棒气动参数如下：

CA,robust=(1±Δ)CA

(9)

式中：Δ是飞行环境不确定性引发的摄动系数；CA,robust为考虑摄动后的气动导数值。

图8是考虑鲁棒性的结冰条件下飞机气动参数变化范围，蓝线和红线分别是Δ=0和Δ=0.5时的升力系数CL、阻力系数CD及俯仰力矩系数Cm；绿色范围为结冰条件下飞机气动参数的容许变化范围。这样，当飞机在恶劣环境下飞行时，只需保证气动参数在容许变化范围内，飞机就可以在具有鲁棒性的动力学边界内根据任务需要进行机动，所以利用图8所示的气动参数计算得到的动力学边界具有很强的鲁棒性。

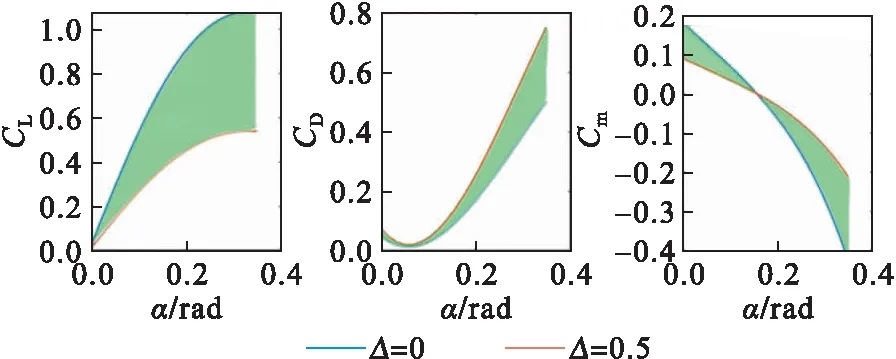
图8 考虑鲁棒性的气动参数范围

下面举例说明鲁棒性动力学边界在保障结冰条件下飞机安全方面的优势，以“结冰探测系统辨识结冰程度η=0.2，但由于机械误差的存在，实际的结冰程度更加严重”为背景。飞机超出动力学边界时将开启边界保护系统使飞行状态收敛至平飞状态。若以η=0.2时的动力学边界作为边界保护系统开启的依据，飞机做机动至α=0.4 rad，θ=0.05 rad，q=-1 rad/s仍被认为是安全状态，但此时飞机已经超出了实际的动力学边界，这时飞机的关键姿态参数很快会发散，飞行状态变化轨线如图9～10所示。

图9 结冰条件下飞机飞行状态

图9中绿色曲面表示Δ=0时的动力学边界，红色曲面表示Δ=0.5时的鲁棒动力学边界，蓝色曲面表示η=0.2时的动力学边界，红色星号表示配平点，黑点表示飞机机动后的初始点，黑色曲线表示由初始点出发的飞机状态轨线。图10为以η=0.2对应的动力学边界作为安全边界时的结冰条件下飞机姿态角变化曲线，可见姿态角很快发散，飞机变得失稳失控。为了避免事故的发生，必须在飞机超出实际安全边界前采取措施，使用本文提出的鲁棒性动力学边界可有效解决这一问题，结冰条件下飞机鲁棒动力学边界保护系统框图如图11所示。

图10 结冰条件下飞机姿态角

图11 结冰条件下飞机鲁棒动力学边界保护系统

图11中红色虚线框内表示结冰条件下飞机鲁棒动力学边界保护系统，当结冰检测系统或气象部门探测到飞机遭遇结冰恶劣飞行环境时，为了保证飞行安全，飞机的关键参数须保持在结冰鲁棒动力学边界内，当飞行状态到达边界时，舵偏控制决策器切换至限幅模式，阻止飞机超出动力学边界。因为采用的动力学边界具有鲁棒性，所以飞机可在超出实际动力学边界之前回稳，从而达到保护结冰条件下飞机飞行安全的目的。

图9中飞机姿态角发散是因为其超出了实际的动力学边界，而迎角、俯仰角速度属于快变量，一旦超出安全阈值很快就会发散，留下的反应时间很短。采用图11所示的结冰条件下飞机鲁棒动力学边界保护系统，在结冰程度η=0.2的情形下做机动，当飞行状态到达边界处，边界保护系统中的限幅器作用使俯仰角速度不能进一步减小，从而使飞行状态保持在安全阈值内，在完成机动后飞机可快速回稳。

使用结冰条件下飞机鲁棒动力学边界保护系统后的飞机姿态变化曲线见图12。图12中实线表示迎角变化曲线，点线表示俯仰角变化曲线，虚线表示俯仰角速度变化曲线。可见采用本文提出的结冰条件下飞机鲁棒动力学边界保护系统，在机动结束后飞机的状态可自发收敛至平衡点。所提方法可保障飞机在结冰情形下的飞行安全，允许飞机在一定状态紧集内做机动，通过限制升降舵的操纵阈值实现限制飞行状态的效果。

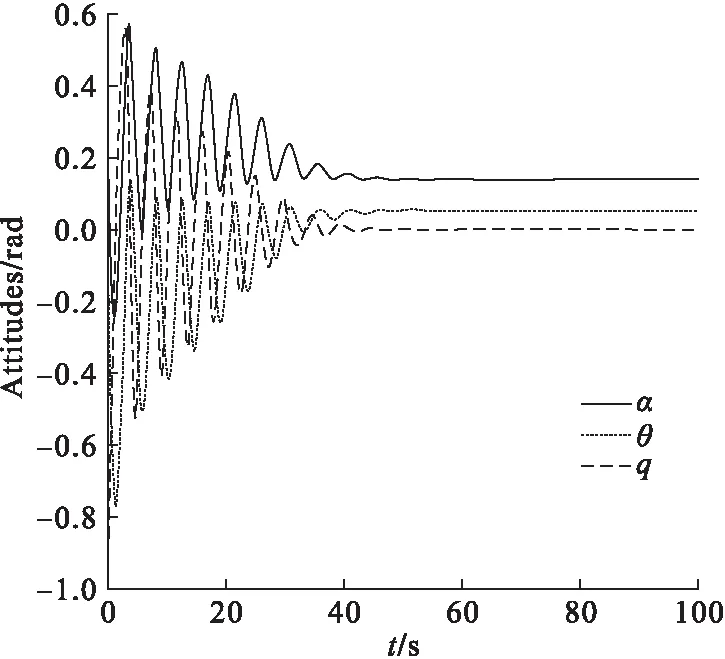
图12 结冰条件下飞机鲁棒动力学边界保护方法下的姿态角

4 结语

本文提出了一种结冰条件下飞机鲁棒动力学边界保护系统设计方法，当飞机遭遇结冰不利飞行环境时，不需获取准确的冰型信息和结冰严重程度，考虑当前结冰检测技术手段，本文提出的方法具有更加广泛意义的工程应用意义。在飞机超出动力学边界之前边界保护系统作用使飞行状态保持在安全阈值范围内，从而保证飞机安全可控。