基于Copula模型的机翼结冰飞行风险定量评估方法研究

段效聪, 徐浩军, 张久星, 易 贤, 宣远勃

(1.空军工程大学航空工程学院，西安，710038；2.93756部队，天津，300131;3.中国空气动力研究写发展中心结冰与防除冰重点实验室，四川绵阳，621000)

飞机遭遇结冰时容易引发诸多不利因素(气动特性恶化、飞行性能下降、空速管等外置传感器读数失真等)的耦合连锁反应，导致人-机-环系统失去稳定性，飞行员操纵不当易引起飞行事故。波音公司统计结果表明，飞机结冰是诱发飞行失控(LOC-I)严重事故的三大因素之一。

飞机结冰后的飞行安全保障是当前研究的热点问题。目前最有效的方式之一是通过开展风险评估，提前预测潜在的结冰区域[1-2]对飞行风险影响的严重程度，进而达到规避结冰高风险区域，保障飞行安全的作用[3]。当前学术界有2种典型的结冰条件下风险预测方法，一种是通过冰形积聚情况来对结冰区潜在飞行风险进行预测[4-6]。另一种是通过结冰后的典型空气动力学特性的改变来判断结冰条件下的风险[7-8]。然而外界条件、积冰冰形、气动参数的改变、飞机气动布局的差异、驾驶员操纵等诸多影响飞行安全的因素最终都要体现在人-机-环复杂系统动力学特性中。因此本文基于人-机-环复杂系统的动力学仿真研究机翼结冰条件下飞行风险的定量评估问题。

飞机遭遇结冰后的飞行动力学特性[9-10]计算是研究飞机结冰致灾风险的前提。如：Bragg教授基于经验估算提出了结冰参数模型[11]，并开发了智能防冰系统[12-13]，有效提升了结冰自动边界保护和结冰自适应飞行控制能力。NASA开展了平尾结冰项目(TIP)，研究了平尾结冰对空气动力学及飞行动力学特性的影响[14-15]。

针对机翼结冰后飞行风险定量评估问题，本文结合蒙特卡罗飞行仿真实验与Copula理论，对结冰条件下人-机-环复杂系统风险定量评估方法进行了研究。对机翼非对称结冰情形下的飞行风险进行了定量计算。所提出的方法完善了现有的飞行安全分析手段，并为结冰条件下飞行风险的指示与规避提供参考与借鉴。

1 机翼结冰后人-机-环动力学建模

机翼结冰使得飞机气动特性发生变化，失速迎角降低，驾驶员的操纵策略、飞机力学特性与环境因素相互影响，考虑到三者之间的相互作用，本文基于飞机运动模型、结冰条件下典型驾驶员模型、结冰影响模型构建了人-机-环复杂系统动力学模型。其中飞机运动模型采用基于四元数法构建的六自由度模型，具体可参考文献[16]。

1.1 结冰条件下典型驾驶员模型

飞机遭遇机翼结冰，影响飞行状态时，驾驶员为恢复姿态进行一定的精准补偿操纵，如图1所示，根据飞机响应输出Y(s)与操纵指令R(s)之间的系统误差E(s)进行修正。驾驶员操纵过程可以分为3个阶段：①经过时间t1发现飞机结冰和飞行姿态改变；②操纵驾驶杆至状态参数反向变化，操纵过程时间为t2；③保持飞机姿态稳定。结冰条件下驾驶员输入输出模型可表示为式(1)，其中F(s)与G(s)为不同的McRuer模型[17]。

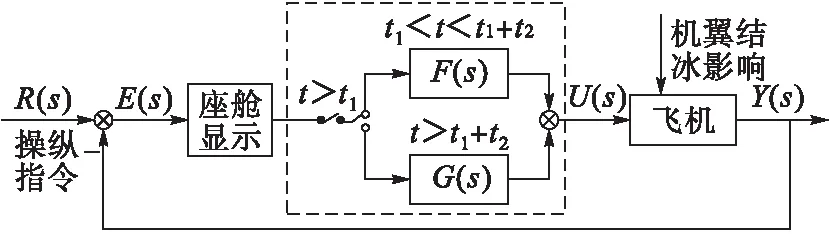
图1 驾驶员补偿操纵模式下的人-机闭环系统

(1)

1.2 结冰影响模型

Bragg教授基于经验估算和风洞试验，提出了结冰影响参量模型。结冰前后的气动导数关系如式(2)所示：

C(A)iced=(1+ηicekCA)C(A)

(2)

式中：C(A)为任一气动导数，C(A)iced为相应的结冰后气动导数；kCA为飞机结冰因子，对于特定飞机，其为定值；ηice为气象因子，通常取值为0～0.3[11]。

2 基于蒙特卡罗仿真实验提取飞参极值

2.1 蒙特卡罗仿真流程

研究结冰条件下内外部影响因素的复杂随机性需要的数据量较大，进行真机自然结冰条件的飞行试验难度高，通过蒙特卡罗仿真实验[18]提取相应的飞行参数极值成为有效的解决途径，仿真实验流程如图2所示。具体步骤如下：

1)设定仿真初始状态的参数。

2)在机翼结冰数据库中根据飞行阶段和任务提取结冰模型关键参数，并计算对飞机气动导数和气动力的影响，同时飞机运动状态的改变亦反馈到结冰模型，提取下一时间的结冰参数。

3)利用蒙特卡罗方法将其他内外部影响条件变量按照其出现频率进行随机抽样。

4)将抽样的变量数值作为检索条件提取飞行员操纵行为特性参数及其他影响飞行状况的条件数据。

5)进行第i次飞行仿真计算。

6)通过系统中总线实时提取多维飞行参数，辨识极值点并存入数据库。

7)本次计算结束后，返回步骤2)开启下一次计算过程，直至迭代循环完成特定点上全部计算次数。

2.2 飞行安全关键参数确定方法

通过选取一次典型的飞机遭遇结冰后驾驶员进行操纵的仿真案例来说明飞行安全关键参数的确定方法。背景飞机选取与A320、波音737和C919为同一量级的典型大型客机。仿真背景设定为：在3 000 m高度，120 m/s速度平飞，在仿真开始5 s后遭遇机翼结冰，设定右侧机翼除冰系统故障。图2所示的是第21次仿真过程中，飞行状态参数的变化情况。

图2 第21次飞行仿真中飞行状态参数变化情况

从图2可以看出，在机翼结冰发生告警之前，由于升力降低、阻力增大，飞机空速略有降低；右侧机翼除冰系统故障无法除冰，飞机在不对称升力和阻力作用下，滚转力矩致使飞机向右侧滚转产生侧滑，并开始急剧掉高度。驾驶员采取增加油门，反向压杆的操纵策略，飞机逐渐恢复到初始状态。在这一过程中，飞机迎角、滚转角、飞行空速和高度变化较大。由于失速迎角降低、横向铰链力矩增大，飞行员难以控制航向稳定。基于此文中选择变化剧烈且对飞行安全较为敏感的迎角、滚转角和飞行空速作为飞行安全关键参数。

2.3 基于一维飞参极值的机翼结冰飞行风险判定条件与量化评估

通过对得到的3个飞行参数极值样本进行统计学分析，发现均具有厚尾分布的特征。采用常见的极值分布模型对提取的飞行参数极值的概率分布和数据序列的边际概率分布尾部进行了建模，通过拟合优度检验验证了3个飞行参数极值样本均服从式(3)所示的GEV分布[18]模型。

(3)

在仿真实验中通常利用飞行关键参数超出安全许用范围来表征飞行风险。由于3个参数的取值范围相差较大，通过归一化处理便于对比分析。飞机迎角与飞行马赫数和襟翼偏度状态有关，考虑结冰对失速迎角的影响，通过αmax/αc(δf，Ma，ice)对迎角极值进行归一化处理。气动手册规定背景飞机滚转角临界值为Φmax=85°；飞机空速左边界值与襟翼偏度和结冰影响有关。

因此结冰条件下飞行风险发生概率可通过式(4)～(6)计算。

(4)

(5)

(6)

3 结冰遭遇情形下三维极值参数Copula模型

结冰导致飞行事故的发生是一个多因素耦合作用下的动态过程，仅仅依靠一维极值参数开展飞行风险定量评估是不全面的，有可能因为参数的选取而导致风险判定的不准确，单一参数的超限不一定导致飞行事故的发生，因此需要综合考虑多个关键参数。

依靠单参数开展研究无法分析参数之间的相依性关系对飞行风险的影响，而多参数条件下的联合分布形式考虑了参数间的相依性结构，能够分析表征参数耦合情形下的分布特征和飞行风险，本文采用的Copula模型便是利用了相同的思路。

3.1 三维极值参数辨识

由Sklar定量和Copula函数的基本性质可知，一定存在一个Copula函数C，满足：

C(F1(Vmin),F2(φmax),F3(αmax))=

F(Vmin,φmax,αmax)

(7)

根据Archimedean族Copular函数性质，构建三维非对称Copular函数结构：

C(u,v,w)=C1(w,C2(u,v))=

(8)

式中φ(·)为阿基米德Copular函数，u,v,w为最小空速极值、滚转角极值、迎角极值的边缘分布，即u=F1(Vmin)，v=F2(φmax)，w=F3(αmax)。φ1和φ2分别对应Copular函数C1和C2，函数φ2由u和v生成，函数φ1由w和φ2生成，假设其参数分别为θ1和θ2，根据式(8)将C2(u,v,θ1)代入C1(w,C2,θ2)即可得到三维Copular函数模型。

对于本文三维极值参数的Copula模型选择，主要有Gumbel Copula模型、Clayton Copula 模型、GS Copula模型、Joe Copula模型。其母函数和Copula三维模型如式(9)～(12)所示。

(9)

C(u,v,w)=

(10)

(11)

(12)

通过辨识得到上述4种Copula模型中的未知参数如表1所示。

表1 参数辨识结果

3.2 拟合优度检验

表2为Copula函数拟合优度检验结果。分析表2可得，Clayton模型和Joe模型的P(K-S)值均大于0.05，在置信水平0.01、0.02、0.05的情况下均能有效通过检验，而其他模型的辨识精度则无法通过检验。进一步比较这2个模型的AIC、BIC和χ2检验值，Joe模型的计算值更低，描述精度更高。

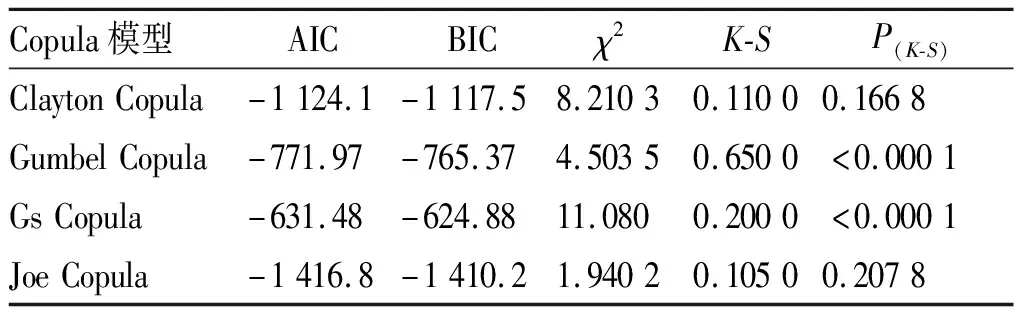
表2 Copula函数拟合优度检验结果

因四维图像不易直观地表征极值参数样本的尾部特性，选择w=0.8，进一步给出Joe Copula模型和Clayton模型的概率密度图，如图3和图4所示。Joe模型和Clayton模型具有很强的耦合性，在高尾部分的风险值较高，而其他区域风险值较低。相较于Clayton模型，Joe模型的风险概率分布更加密集，高尾部分的分布密度梯度更大，对后尾特性描述更好，因此选择Joe模型作为机翼非对称结冰情形下最小空速极值、滚转角极值和迎角极值的描述模型。

图3 Joe模型分布概率密度和累积概率图

图4 Clayton模型分布概率密度和累积概率图

3.3 三维参数极值Copula模型飞行风险概率计算

根据构建的飞行风险判定条件，依据Joe Copula模型，求解飞行风险概率如式(13)所示：

Pr=1-CJoe(F1(Vmin/Vc(δf,ice)>1，

F2(φmax/85>1),F3(αmax/αc(δf,Ma,ice)>1)

(13)

式中：Cjoe代表基于式(12)求解的Joe Copula模型。

将辨识得到的参数带入式(12)和(13)，求得飞行风险概率为0.062 4，参考MIL-STD-882D标准，飞行风险已经达到B极，此时需要飞行员密切关注飞行状态的变化。运用Joe Copula函数计算出的风险概率值较高，一定程度上反映了参数耦合特性对飞行风险事件演化的影响，考虑多个飞行参数极值构建联合概率分布模型，能够更加全面地分析样本数据所蕴含的风险信息。

4 结论

1)基于仿真案例确定了机翼非对称结冰条件下迎角、滚转角和飞行空速对飞行安全影响最大。利用蒙特卡罗仿真实验提取多组飞参极值，基于安全许用范围建立风险判定依据，利用辨识得到的三维极值模型参数进行拟合优度检验，并计算出符合该三维极值模型的飞行风险概率。

2)所提出的机翼结冰飞行风险定量评估方法可以定量评估机翼非对称结冰对飞行安全的影响。由于飞行安全受到多种因素影响，在评估飞行风险时不可能将所有因素均考虑在内。文中所计算的风险值在某种程度上只是一个参考值，但可以作为一种客观的指标，为分析飞机结冰科目试飞风险提供理论依据，科学地衡量机翼结冰情形对飞行安全影响的严重程度。