对2020年全国卷Ⅰ理科第20题的多视角探究

◇ 江西 李树森 孙 强

直线与圆锥曲线的综合问题是高考的重点、热点问题,此类问题往往运算量大.解决此类问题常常需要将题干中的几何条件转化为坐标形式,其关系式中需要含有x1＋x2和x1x2,并运用根与系数的关系求解,但是有一类问题其坐标形式中不会出现x1＋x2和x1x2,解决此类问题就需要抓住x1与x2或y1与y2的系数不相等(非对称),借助曲线方程、代数变形、和与积关系的转换等手段,调整为对称.本文以2020年全国卷Ⅰ理科第20题为例,从五种不同的视角探究这一类问题的解题策略.

1 试题呈现

题目(2020年全国卷Ⅰ理科第20题)已知A,B分别为椭圆的左、右顶点,G为E的上顶点为直线x＝6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

图1

(1)求E的方程;

(2)证明:直线CD过定点.

2 命题背景

1)极点、极线定义:已知圆锥曲线Γ:Ax2＋By2＋Cx＋Dy＋F＝0,则称点P(x0,y0)和直线l:别是圆锥曲线Γ的一对极点和极线.

2)定理(配极原则):点P关于圆锥曲线Γ的极线p经过点Q⇔点Q关于圆锥曲线Γ的极线q经过点P⇔直线q关于圆锥曲线Γ的极点Q在直线p上.由此定理可知,共线点的极线必共点,共点线的极点必共线.

3 试题分析

本题是一道典型的直线与圆锥曲线综合问题,涉及的直线多、点多,是一道关系错综复杂的动态问题.同时在本题中出现了一对关于原点的对称点,具有很多重要的性质.涉及多线与多点的问题,常常需要我们选择主动线、主动点来处理,如何巧设变量、建立关系更值得我们深思.问题中直线CD与两个不同点关联,因此利用几何关系得出来的x1与x2或y1与y2的关系,一般会出现不对称,直接利用根与系数的关系处理比较困难,如何突破化简运算更是一个重要的环节.下面从设点和设线两种方向处理,围绕着如何突破运算,深入探究本题第(2)问的解法.

4 解法探究

视角1选择P为主动点,设单参数并表示直线CD的直线方程.

解法1因为A(－3,0),B(3,0),设P(6,d),则直线PA,PB的方程分别为

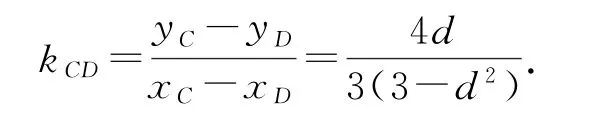
直线CD的方程为

故得直线CD过定点.

点评

此方法处理过程中视动点P为主动点,设点P(6,d),并通过联立直线PA,PB与椭圆方程,利用根与系数的关系直接求解出C,D的坐标,并求出直线CD的方程,对直线方程适当变形得到直线CD过定点这种方法很常见,但是运算量大,对代数的变形能力要求高.

视角2通过直线CD的特殊位置猜想其定点,并设点转化为共线向量证明其结论成立.

解法2由对称性可知,直线CD必经过x轴的定点,且CD⊥x轴.

设C(x0,y0),D(x0,－y0),得A(－3,0),B(3,0),设P(6,d),则即kPB＝3kPA.

因为C,H,D三点共线,则设C(x1,y1),D(x2,y2),则

因为C(x1,y1),D(x2,y2)为椭圆上的点,则有

点评

此方法的处理过程中巧妙利用对称关系,并取特殊位置猜想并计算直线CD经过的定点.本题中由于动点P为主动点,利用斜率kPB＝3kPA的关系变换视角,只要证明直线CD经过定点0)时,满足斜率kBD＝3kAC.此时A,B不是同一个点,直接设直线,其坐标形式不具备对称性,难以处理,转成设C,D的坐标,并利用定比分点寻找坐标之间的关系,根据点C,D在椭圆上(类似“点差法”原理)对式子先进行一次系数乘法后相减直接得到x1＋λx2,x1－λx2,这和定比分点相呼应,利用λ表示x1,x2,可证明kBD＝3kAC成立.

视角3选择直线CD为主动线,设CD直线方程,并利用两根的和与积的关系转化,利用方程思想求解.

解法3设直线CD的方程为x＝my＋n,C(x1,y1),D(x2,y2).联立方程得

又因为x1＝my1＋n,x2＝my2＋n,整理得

点评

本题动点P为主动点,利用kPB＝3kPA的关系变换视角,视直线CD为主动,设直线CD的方程x＝my＋n,根据斜率之间关系kBD＝3kAC,寻找两个参数m,n间的等量关系.利用直线代点统一坐标,得出的关系－2my1y2＋(n＋3)y2＋(9－3n)y1＝0不具备对称性,根与系数的关系难以处理,但注意到式子出现y1y2,和y1,y2,故可以将积y1y2向y1＋y2转化,从而得到再通过代入即可求出的值.

视角4选择直线CD为主动线,设CD直线方程,巧用曲线方程代入转化为对称.

解法4因为A(－3,0),B(3,0),设P(6,d),C(x1,y1),D(x2,y2).所以3kAP,所以kBD＝3kAC,即

因为C,D在椭圆上,则

由式①可得

将式②代入式③得

设直线CD的方程为y＝kx＋m,联立可得

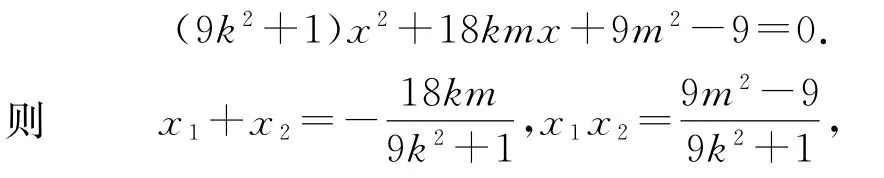
代入式④得

得3k＋2m＝0或m＋6k＝0(此时CD过点(－6,0),不在椭圆内,m＋6k＝0不符合题意),所以直线CD的方程为,即CD过定点.

点评

本题将动点P设为主动点,利用kPB＝3kPA的关系变换视角,设直线CD的方程为y＝kx＋m,根据斜率之间关系kBD＝3kAC.由于A,B不是同一个点,但是它们关于原点对称,利用曲线上点满足曲线方程,整体代入,实现了对称化,利用根与系数的关系求解得到参数k,m之间的关系,从而得到直线CD经过定点.

视角5抓住斜率关系,转化为同一点斜率的乘积关系,化齐次式处理.

解法5因为A(－3,0),B(3,0),设P(6,d),C(x1,y1),D(x2,y2),则即kPB＝3kPA.由椭圆的第三定义可得则有.

设直线CD的方程为m(x＋3)＋ny＝1,C(x1,y1),D(x2,y2).椭圆方程9,即(x＋3)2－6(x＋3)[m(x＋3)＋ny]＋9y2＝0,即(1－6m)(x＋3)2－6n(x＋3)y＋9y2＝0.两边同时除以(x＋3)2,得

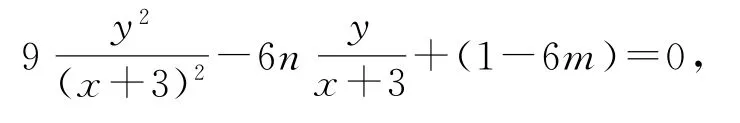
则有

点评

利用kPB＝3kPA的关系变换视角,利用椭圆的第三定义得将其转化为.其中y1y2计算比较复杂,可构造关于的一元二次方程,再根据根与系数的关系处理.直线CD显然不过点(－3,0),可设为m(x＋3)＋ny＝1,将椭圆的方程的标准方程变形为(x＋3)2－6(x＋3)×1＋9y2＝0,将式子中的“1”利用直线方程代入得(1－6m)(x＋3)2－6n(x＋3)y＋9y2＝0,实现了二次齐次化,再在两边同时除以(x＋2)2,便构造了关于的二次方程,最后通过根与系数的关系求解即可.

5 问题变式

根据极点、极线中的配极原则,共点线的极点必共线,此考题还可以变式为如下.

变式如图2所示,已知A,B分别为椭圆E:的左、右顶点,G为E的上顶点,作直线与椭圆E相交于C,D两点,直线AC,BD相交于点P.

(1)求E的方程;

(2)证明:点P在定直线上.

图2

6 同源真题

(2010年江苏卷)在平面直角坐标系xOy中,如图3所示,已知椭圆的左、右顶点为A,B,右焦点为F.设过点T(t,m)的直线TA,TB与此椭圆分别交于点M(x1,y1),N(x2,y2),其中m＞0,y1＞0,y2＜0.

图3

(1)设动点P满足|PF|2－|PB|2＝4,求点P的轨迹;

(3)设t＝9,求证:直线MN必过x轴上的一定点(其坐标与m无关).

7 回顾反思

在数学学习的过程中,我们能够发现一道题目可以用许多方法来解答,此时需要灵活运用条件从多个视角进行思考.本文对2020年的一道圆锥曲线试题进行探究,可知圆锥曲线综合问题处理途径主要是围绕着两条主线来展开.

1)设点法,针对“多动”问题,寻找主动点,巧设参数,用此参数表示其他相关点,例如解法1和解法2;

2)设线法,针对多条动直线,寻找主动直线,设直线方程处理问题,例如解法3、解法4和解法5.

直线与圆锥曲线的综合问题是支撑高中数学知识体系的重点内容,同时圆锥曲线问题的解决具有入口宽、方法灵活多样等特点,用不同的解题途径,其运算量就有繁简之分.解析几何中常常有一类问题,将几何条件转化为坐标形式,其关系式子中不含x1＋x2和x1x2,呈现非对称的特征,会导致运算量增大,本文从多种途径优化运算.

1)利用曲线上的点满足曲线方程,整体代入,将非对称问题转化为对称问题;

2)利用两根和与积之间的关系,将两根积转化为和,通过方程思想求解;

3)利用椭圆的第三定义转换关系,实现对称化处理;

4)对数学的关系式进行合理构造,利用斜率的积与和之间的关系结合根与系数的关系,将曲线方程转化为“二次齐次式”,并根据齐次式的特征,将两变量化为斜率形式,从而解决问题.

波利亚有句名言:“发现问题比解决问题更重要.”在圆锥曲线的教学中,要启发学生多角度、多层次去思考问题、解决问题,同一个知识点若使用的角度不同、使用的先后顺序不同,其效果也就大不一样.因此我们必须审时度势、巧妙地运用这些知识点,从而使问题得到简化,更要引导学生提炼一般模型及解法,达到举一反三的目的,从根本上提升学生的数学素养.