针对裂变产额和半衰期的燃耗计算灵敏度和不确定度分析方法
韩丰林,祖铁军,吴宏春,曹良志
(西安交通大学 核科学与技术学院,陕西 西安 710049)
输入参数、数学物理模型近似和数值离散方法等引入的不确定度会影响核反应堆物理计算结果的精度,随着反应堆物理计算方法的发展,数学物理模型近似及数值离散方法所引入的不确定度显著降低,而输入参数对计算结果的影响变得更加重要[1-3]。核数据是反应堆物理计算中最基础的输入参数,它主要是基于核物理实验测量、核反应模型理论分析、核数据评价建库及宏观检验产生的。由于核物理测量的不确定度、核反应理论模型的局限性和近似、核数据评价的主观性、群常数加工制作中的近似等因素,核工程应用中的核数据存在一定的不确定度。
核反应堆燃耗计算得到的原子核密度、有效增殖因数等响应参数,在核反应堆设计、安全分析及乏燃料处置中十分重要。分析核数据的不确定度在燃耗计算中的传递,量化燃耗计算宏观响应的不确定度,对提高核反应堆的安全性、经济性及高放射性废物的妥善处置有着积极意义。另外,目前评价核数据库中的裂变产额数据缺乏足够的独立产额测量数据和协方差数据[4],通过灵敏度分析确定对目标参数计算精度影响较大的裂变产额数据,对核数据的改进有指导意义[5]。
目前国内外基于抽样方法及微扰方法对燃耗计算响应参数的灵敏度和不确定度开展了一定研究[6-7],但多针对核反应截面开展,缺乏对裂变产额和半衰期等核数据的分析。2013年,国际核数据评价合作工作组(WPEC)把量化裂变产额对响应参数引入的不确定度作为未来工作目标之一。对于多输入参数、少输出参数的数值模拟系统,微扰方法与抽样方法相比计算效率较高,且可给出响应参数对各输入参数的灵敏度系数。
本文基于广义微扰理论推导燃耗计算参数对于裂变产额和半衰期的相对灵敏度系数计算理论模型,并在西安交通大学自主研发的程序NECP-SUNDEW[8-9]基础上实现有效增殖因数和原子核密度等宏观响应对裂变产额和半衰期的灵敏度计算,用直接数值扰动方法进行验证。以UAM[10-11]基准题的TMI-1栅元为对象,基于ENDF/B-Ⅶ.1数据库量化由裂变产额和半衰期引入的响应参数不确定度。
1 理论模型
微扰方法量化不确定度首先需计算出系统的输入参数对于输出响应参数的灵敏度,然后基于灵敏度和输入参数的协方差数据采用“三明治法则”进行不确定度计算,即可获取输出参数的不确定度[12-13]。不确定度的计算公式为:
(1)
式中:SD(R)为输出参数的相对不确定度;Sσ为响应参数R对于核数据σ的相对灵敏度系数矩阵;COVσ为核数据σ的相对协方差矩阵。
1.1 燃耗灵敏度计算方法
对于系统的响应参数R,如果它是输入参数α的函数,输入参数α的改变造成的响应参数R的相对变化量被定义为响应参数R关于输入参数α的相对灵敏度系数S,其表达式为:
(2)
在核反应堆物理计算中,响应参数R可表达为:

Φ*(r,E,Ω,t))drdEdΩdt
(3)
式中:N为原子核密度;Φ为中子角通量密度;Φ*为共轭中子通量密度;r为位置;E为能量;Ω为角度;t为时间。
将式(2)关于核数据σ进行一阶泰勒展开:
(4)
式中:t0为燃耗起始时刻;tf为燃耗的结束时刻;t为时间。式(4)右边第1项是灵敏度系数的直接影响项,是由核数据的变化直接引起的响应参数的变化;后3项是间接影响项,是由核数据的变化引起的各核素的原子核密度、中子通量密度、共轭中子通量密度的变化,并最终造成响应参数的变化。由式(4)可知,求解灵敏度系数S需给出中子通量密度Φ、共轭中子通量密度Φ*及原子核密度N对于核数据的微分。燃耗计算的基本方程为:
(5)
Bi,g(r)ψi,g(r,Ω)=0
(6)
(7)
(8)

将式(5)~(8)关于核数据σ求微分,可得到计算式所需的各微分项。若核数据为裂变产额和半衰期,经推导可得到相对灵敏度系数计算式:
(9)
式中:I为燃耗总步数;N*为共轭原子核密度,由下式得到:
(10)
式中,MT为燃耗矩阵的转置矩阵。
将燃耗矩阵中与半衰期和单群中子通量相关的部分分开,可写成以下形式:
M=Mλ+Mφ
(11)
式中:下标λ表示燃耗矩阵中由核素衰变引起的转换;下标φ表示燃耗矩阵中由中子引起的转换。
结合式(11)计算式(9)中的微分项可得到相对灵敏度系数。
1.2 裂变产额协方差计算方法
独立裂变产额为裂变直接产生的裂变产物的产额,具有相同质量数的若干裂变产物组成1条质量链。评价核数据库中给出的各独立裂变产额处于同一条质量链时,相互之间有较大的负相关性[14]。直接使用评价核数据库中给出的各独立裂变产额标准差数据进行不确定度计算,则忽视了独立裂变产额的相关性,会明显高估裂变产额引入的不确定度。本文采用Katakura[15]给出的最小二乘法计算式产生独立裂变产额协方差矩阵,可考虑同一质量链中各独立裂变产额的相关性,裂变产额协方差矩阵的对角线元素μii和非对角线元素μij分别为:
(12)
(13)
式中:Δyi为独立裂变产额yi的标准差;ΔY为质量产额的标准差;j为同一质量链中的各裂变产物。
在反应堆物理计算程序的燃耗计算中,一般不采用包含评价核数据库中全部核素的精细燃耗链,而是在不影响计算精度的前提下,采用压缩燃耗链以降低计算资源的需求量。独立裂变产额协方差矩阵包括评价核数据库中全部裂变产物,需处理得到与压缩燃耗数据库相一致的裂变产额协方差矩阵。压缩燃耗数据库中的裂变产额由精细燃耗数据库中的独立裂变产额按照衰变分支比累积得到,所以压缩燃耗数据库的裂变产额协方差矩阵可表示为:
(14)
(15)
式中:A和B均为压缩燃耗数据库中的裂变产额;y为独立裂变产额;a和b为由独立裂变产额到压缩燃耗数据库中裂变产额的转化关系。
1.3 程序开发

2 数值结果
本文计算的问题是世界经济合作与发展组织核能机构(OECD/NEA)的不确定度分析基准题(UAM)中的TMI-1栅元,计算基于热态满功率条件,燃耗期间的平均功率为33.58 W/gU。基准题的几何结构如图1所示,表1列出材料信息。本文输运计算使用69群的多群截面数据库,燃耗计算使用基于定量化分析方法[17]制作的适用于压水堆物理计算的压缩燃耗数据库,其中包括195种裂变产物。裂变产额和半衰期的不确定度数据来自ENDF/B-Ⅶ.1数据库,并经过处理得到压缩燃耗数据库的裂变产额协方差矩阵,其中裂变产额协方差数据考虑的裂变核素包括235U和239Pu。图2示出压缩燃耗数据库的235U热中子裂变产额协方差矩阵。

图1 TMI-1栅元几何结构Fig.1 Geometry structure of TMI-1 pin-cell

表1 TMI-1栅元材料信息Table 1 Composition of material of TMI-1 pin-cell

图2 235U热中子裂变产额协方差矩阵Fig.2 Fission yield covariance matrix for 235U thermal neutron
2.1 灵敏度分析
使用直接数值扰动方法对基于广义微扰理论计算的燃耗相对灵敏度系数进行了验证。表2、3分别列出TMI-1栅元的无限增殖因数kinf及135I原子核密度对于裂变产额和半衰期的相对灵敏度系数,其中核数据235U_135I表示235U裂变产生135I的产额,GPT和DP分别表示广义微扰理论和直接数值扰动方法。结果表明,广义微扰理论与直接数值扰动方法计算得到的相对灵敏度系数结果偏差很小,证明了开发的燃耗灵敏度系数计算程序的正确性。由相对灵敏度系数计算结果可知,栅元的kinf对裂变产额和半衰期等核数据的相对灵敏度系数较小;而135I原子核密度受裂变产额和半衰期影响明显,具有较大的相对灵敏度系数。
原子核密度对于裂变产额和半衰期的相对灵敏度系数由具体的燃耗转化关系决定。以135Xe的原子核密度为例,图3示出其相对灵敏度系数,图4示出燃耗计算中135Xe的燃耗链。135Xe的原子核密度对135I裂变产额及135Xe半衰期的相对灵敏度系数较大,这是由于135Xe本身的裂变产额较小,其产生主要来自135I的衰变,而135Xe的衰变使其消失。随燃耗深度的增加,235U裂变产额的相对灵敏度系数变小,而239Pu裂变产额的相对灵敏度系数变大,这是由于燃耗过程中235U的消耗和239Pu的累积造成的。

表2 kinf的相对灵敏度系数Table 2 Relative sensitivity coefficient of kinf

表3 135I原子核密度的相对灵敏度系数Table 3 Relative sensitivity coefficient of 135I nuclide concentration
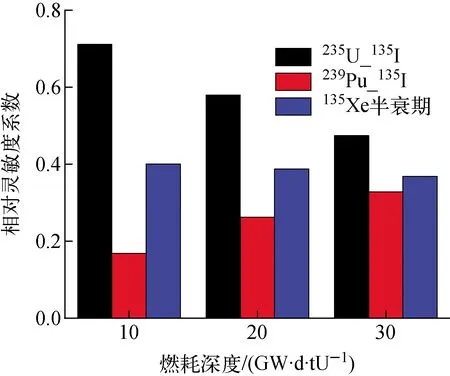
图3 135Xe原子核密度的相对灵敏度系数Fig.3 Relative sensitivity coefficient of 135Xe nuclide concentration

图4 135Xe燃耗链Fig.4 135Xe burnup chain
2.2 不确定度分析

图5 裂变产额引入的原子核密度的相对不确定度Fig.5 Relative uncertainty of nuclide concentration from fission yield
基于灵敏度分析的结果,量化了裂变产额和半衰期数据对TMI-1栅元的无限增殖因数kinf和原子核密度计算结果引入的相对不确定度。图5示出寿期末(燃耗深度为60 GW·d/tU)一些核素的原子核密度由裂变产额引入的相对不确定度。结果表明,考虑裂变产额相关性后相对不确定度的计算结果显著降低。对于栅元kinf,半衰期引入的相对不确定度极小可忽略,在寿期末仅为0.001%。裂变产额引入的相对不确定度在燃耗过程中的变化如图6所示,考虑裂变产额相关性后相对不确定度同样显著降低,在寿期末仅为0.06%。对于原子核密度,表4列出寿期末重要裂变产物的原子核密度由裂变产额(考虑相关性)和半衰期数据引入的相对不确定度。结果表明:半衰期引入的相对不确定度均较小,但151Eu除外,这是由于151Eu的原子核密度对151Sm半衰期的灵敏度很大,而151Sm半衰期具有8.9%的标准差;而裂变产额引入的相对不确定度相对较大,其中109Ag原子核密度的相对不确定度达到9.9%,主要是由于对应的独立裂变产额和质量产额数据有较大的相对不确定度。对于寿期末重核的原子核密度,裂变产额(考虑相关性)和半衰期数据引入的相对不确定度均在0.1%以下。本文对TMI-1栅元的kinf和原子核密度相对不确定度的计算结果与Cabellos等[18]使用统计学抽样方法和精细燃耗链获得的相对不确定度结果符合。

图6 裂变产额引入的kinf的相对不确定度Fig.6 Relative uncertainty of kinf from fission yield
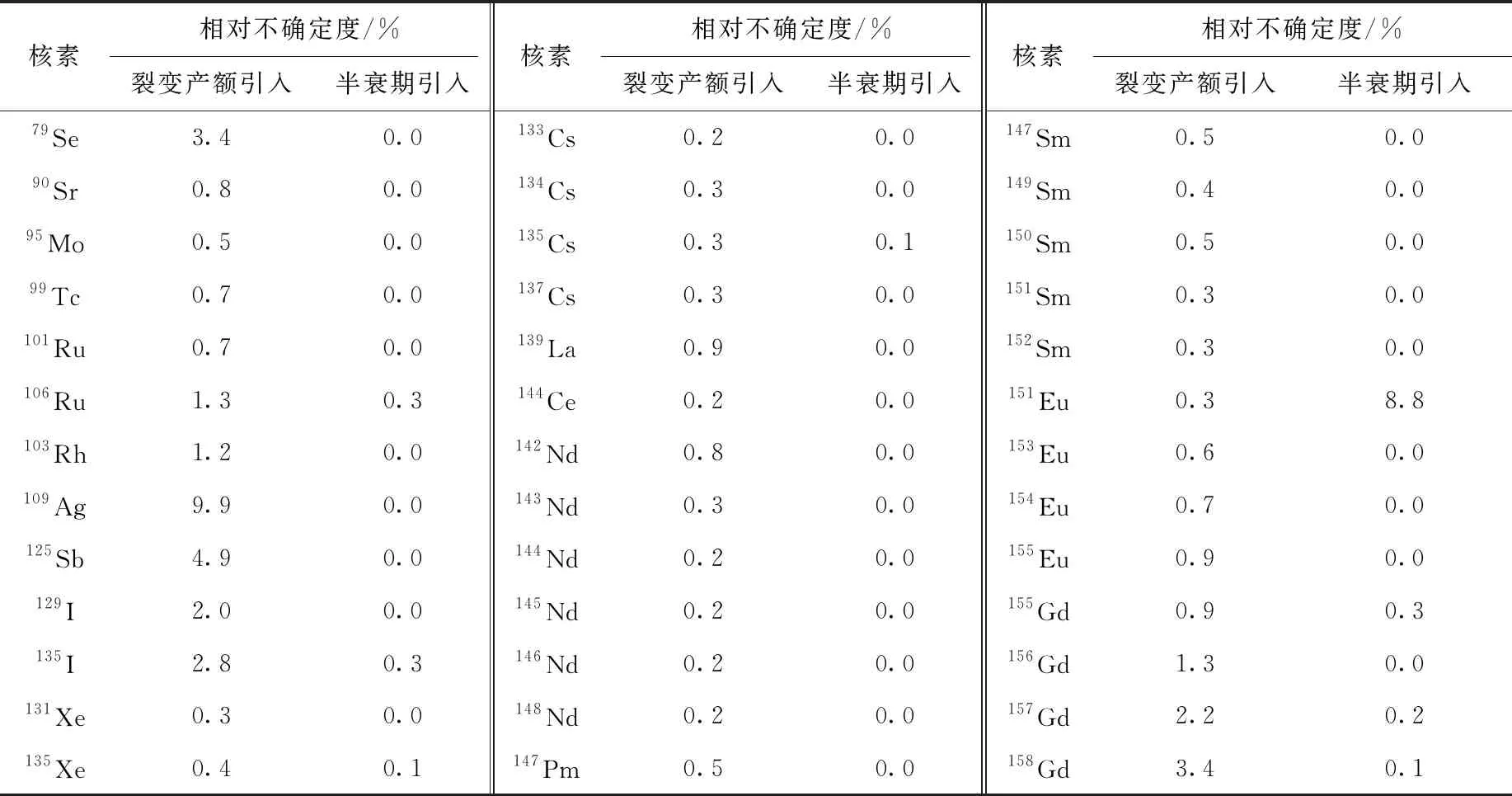
表4 裂变产物原子核密度的相对不确定度Table 4 Relative uncertainty of fission product nuclide concentration
3 小结
基于广义微扰理论推导了燃耗计算响应参数对于裂变产额和半衰期的灵敏度计算模型,在NECP-SUNDEW的基础上开发了裂变产额和半衰期的灵敏度和不确定度分析功能。使用开发的程序计算了UAM基准题TMI-1栅元kinf和原子核密度对各种裂变产额和半衰期数据的灵敏度,并用直接数值扰动方法对计算结果进行了验证。发现栅元kinf对于裂变产额和半衰期的灵敏度较小,而原子核密度对于裂变产额和半衰期的灵敏度较大,由具体的燃耗转化关系决定。考虑裂变产额的相关性,产生了针对压缩燃耗数据库的裂变产额协方差矩阵,并量化了栅元kinf和原子核密度由裂变产额和半衰期引入的相对不确定度。栅元kinf由半衰期引入的相对不确定度可忽略,由裂变产额引入的相对不确定度很小,在寿期末仅为0.06%。裂变产额和半衰期对部分裂变产物的原子核密度会引入较大的相对不确定度,如109Ag和151Eu。

