GASFLOW中气溶胶再悬浮模型与RnR模型对比研究
黄 挺,江 斌,陈 炼
(国核华清(北京)核电技术研发中心有限公司,北京 102209)
核电厂发生严重事故的情况下,放射性气溶胶会由一回路释放进入安全壳的气空间,并随时间的推移沉积在安全壳或各类设施的表面上。当出现氢气爆燃及由于安全壳失效或通风产生的压力骤降等现象时,安全壳内产生的瞬时高速气流会导致沉积的气溶胶再次悬浮于气空间中,使得安全壳内裂变产物浓度再度升高,对安全壳中晚期的放射性源项的释放量产生较为明显的影响。因此,为更为准确地评估严重事故下的放射性源项的释放量,需在对气溶胶再悬浮机理深入研究的基础上开发相应的再悬浮计算模型。
目前,国际上在气溶胶再悬浮领域进行过较多理论及试验研究,发展出不同的气溶胶再悬浮模型,其中部分已经过试验的验证,并在核电厂严重事故分析程序中获得了一定的应用[1-2]。国内近些年也对气溶胶再悬浮理论及模型的适用性开展了较为广泛的研究[3-5]。再悬浮模型通常可分为两类[6]:一类是基于力学平衡原理,认为流场中沉积气溶胶颗粒的受力平衡被打破时即发生再悬浮,该类模型被统称为力学平衡模型,GASFLOW程序中的气溶胶再悬浮模型即属于该类模型;一类是基于能量累积的原理,认为流场中沉积气溶胶颗粒所获得的能量足以克服表面黏附作用时即发生再悬浮,该类模型被称为能量累积模型,其中比较有代表性的是Reeks等[7-8]提出的RnR模型。
GASFLOW是由美国洛斯阿拉莫斯国家实验室(LANL)和德国卡尔斯鲁厄研究中心(FzK)共同开发的三维计算流体力学程序[9],主要描述流场中的三维流动现象:氢气的扩散、混合分布与分层;氢气燃烧和火焰扩散;不可凝气体的分布对本地凝结与蒸发的影响;气溶胶的夹带、传输与沉降等[10]。目前GASFLOW主要应用于安全壳内热工流体学现象的模拟和氢气风险的评估。GASFLOW中用于模拟气溶胶行为的模型包括:拉格朗日离散粒子输运模型、随机湍流粒子扩散模型、粒子沉降模型、粒子再悬浮模型及粒子云模型[11]。目前对于GASFLOW中气溶胶模型,尤其是再悬浮模型的相关研究及应用较少,有必要对其适用性及适用范围进行深入研究及探讨。
本文以GASFLOW为基础,通过与RnR模型分析结果及相关验证试验数据的对比研究,对程序中再悬浮模型的适用性进行评估,在此基础上为GASFLOW中再悬浮模型的改进提出建议。
1 模型描述
1.1 GASFLOW再悬浮模型
GASFLOW中采用了力学平衡模型,该方法通过获取沉积壁面的固体颗粒在平行壁面气流中的最小拾取速度,来判定其是否发生再悬浮[11]。图1为稳定且完全发展的湍流场中,静止于壁面的单一球形颗粒的受力分析示意图,所受各力如下。
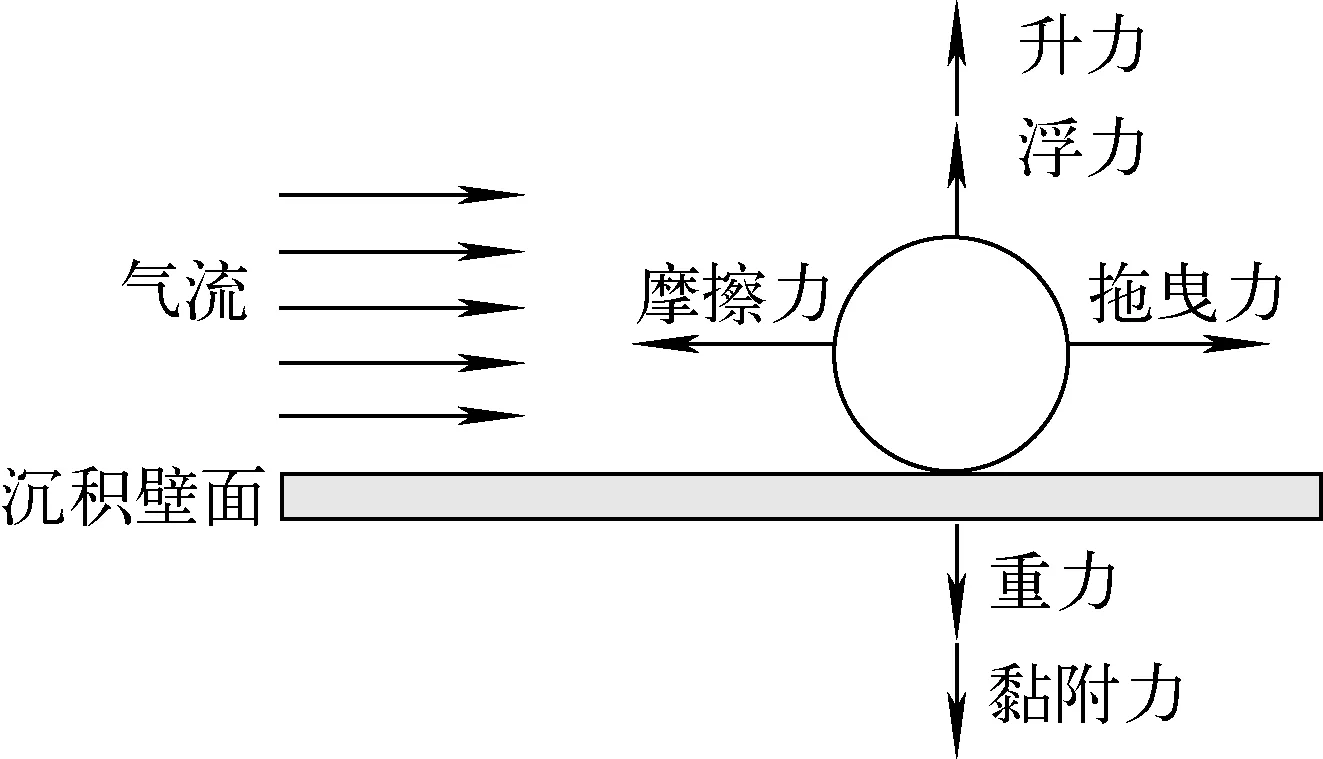
图1 稳定且完全发展的湍流场中 静止于壁面的单一球形颗粒的受力Fig.1 Forces acting on single sphere at rest on wall with steady and fully developed turbulent flow
重力Fg为:
(1)
浮力Fb为:
(2)
黏附力Fa[12]为:
(3)
拖曳力Fd为:
(4)
升力Fl[13]为:
(5)
摩擦力Ff为:
Ff=fsFn=fs(Fg+Fa-Fb-Fl)
(6)
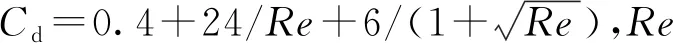
当拖曳力等于摩擦力时,气溶胶颗粒开始运动并离开沉积表面,此时:
Fd=fs(Fg+Fa-Fb-Fl)
(7)
将式(1)~(5)代入式(7)中,可得:
(8)
式(8)是以Ugcp为未知数的方程,通过求解该方程可得出单一颗粒发生再悬浮的最小气流速度,将其用Ugpu表示。为考虑气溶胶再悬浮的统计特性,用式(9)计算再悬浮概率PRBntrn:
(9)
1.2 RnR模型
Reeks等[14]提出了最早的能量累积模型,即RRH模型。RRH模型假设通过脉动抬升力导致湍流能量的传递。在脉动抬升力的频率与粒子固有表面振动频率相差不大时,该模型允许共振能量的传递。Reeks等通过详细考虑表面黏性势阱上的随机运动,在Johnson等[15]提出的黏附力模型的基础上,推导出与分子表面脱附率相似的再悬浮率常数公式,即:
(10)
其中:p为再悬浮率常数;n为黏附势阱中颗粒表面振动频率;Q为取决于黏附力和平均抬升力的差值的势垒高度;〈PE〉为势阱内颗粒的平均势能。
一系列试验及分析结果表明,在使用RRH模型进行分析时总会对气溶胶的再悬浮率估计过低。为对RRH模型进行改进,Reeks等[7]考虑了粗糙表面的颗粒再悬浮情况,提出了RnR模型。
图2示出RnR模型中颗粒与表面接触示意图[7]。当湍流流经该表面时,颗粒受到抬升力FL、拖曳力FD、重力mg和黏附力Fa的作用,其中FL是图1中升力和浮力的合力。颗粒由于FL和FD的作用,在抵消Q点Fa的同时不断振动,直到获得足够的旋转能量来打破与Q点的连接。该情况一旦发生,颗粒将自由滚动,或由于FL足够大而破坏其与P点的连接,这两种情况均认为颗粒发生了再悬浮。
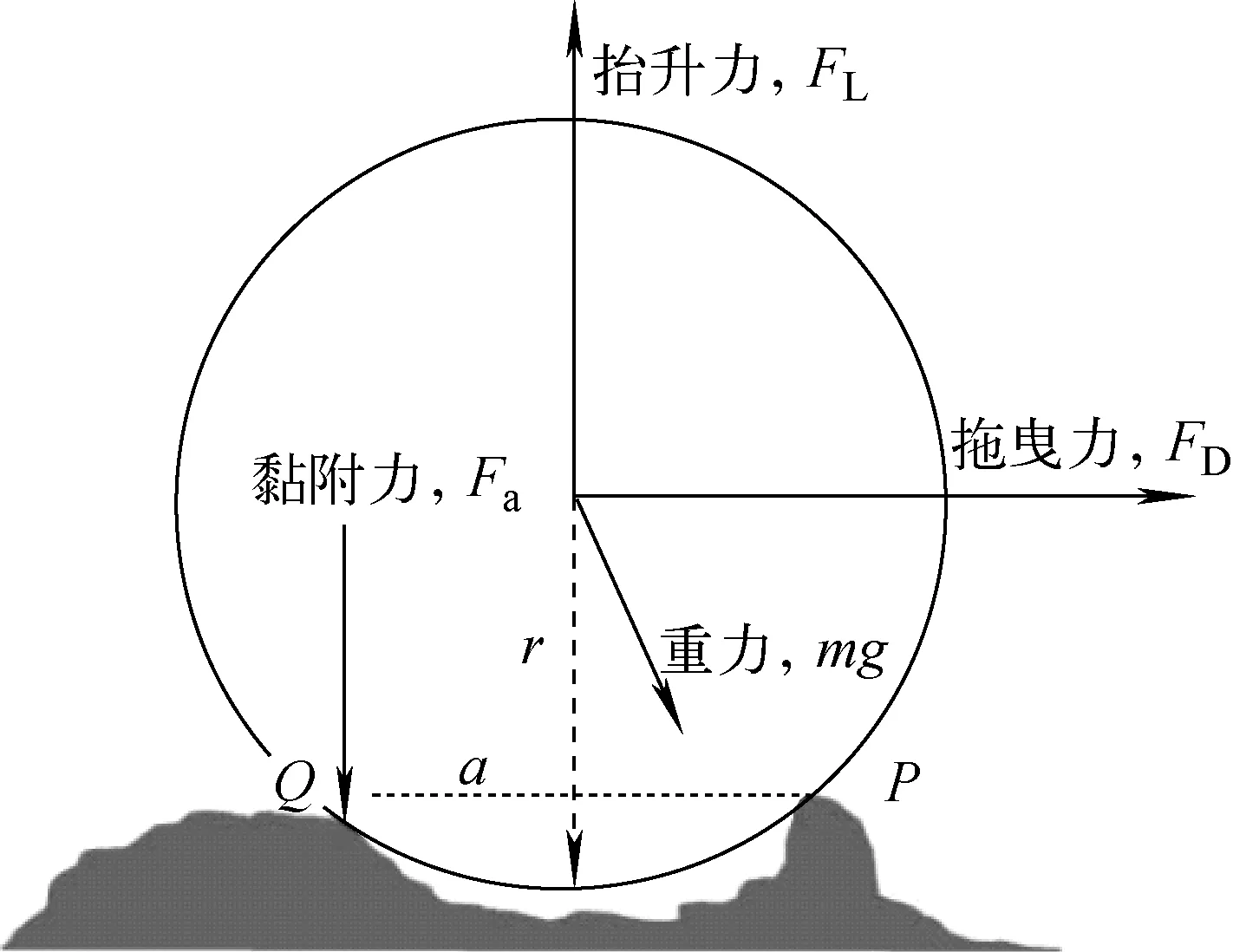
图2 RnR模型颗粒与表面接触关系[4]Fig.2 Particle-substrate contact for RnR model[4]
RnR模型中的再悬浮率常数仍采用式(10)的形式,但式中的n和〈PE〉取决于粒子在P点的扭矩和转动惯量,其中拖曳力的贡献更大。再悬浮率常数公式为:
(11)
其中:nθ为黏性势阱中颗粒表面振动频率;k为与表面势场形态相关的数值常数;a为两个凸起点的间距;r为颗粒半径;mgn和mgt分别为颗粒重力的法向和切向分量;η为近共振与偏共振对〈PE〉贡献的比值;〈F〉和〈f2〉为F(t)的均值和协方差,F(t)定义如下:
(12)
黏附力Fa一般假设为对数正态分布的形式,在计算中通常在法向和切向进行分解并分别考虑。
2 几何建模及计算条件
2.1 几何建模
Reeks等[7]对RnR模型进行了验证,其试验段为一长度为5 m、管口尺寸为0.2 m×0.02 m的方形管道,气流从一侧管口进入,沉积的气溶胶位于气流下游3.5 m处。试验在常温、常压下进行,气流速度范围为0.08~6 m/s。
试验气溶胶工质的总质量等于滞留的气溶胶质量加上再悬浮气溶胶的质量,即再悬浮率=1-滞留份额。一般来说,气溶胶的滞留份额相对容易测得。Reeks等在试验中选择测量气流通过1 s后的气溶胶滞留份额,并与RnR模型的计算结果进行了对比。
根据上述试验设计参数及条件,利用GASFLOW建立试验段管道几何模型,设定初始状态下气溶胶的沉积区域如图3所示。
通过在x、y和z方向分别设置21、17和9个节点,得到2 560(20×16×8)个有限元网格。由于气溶胶颗粒的再悬浮与其所处网格处的气流速度密切相关,考虑到网格划分可能对分析结果造成的影响,分别针对网格数为2 560、20 480(40×32×16)和163 840(80×64×32)等3种情况,计算气流速度为0.5 m/s条件下的管内流场。气溶胶所处网格内的气流平均速度分别为0.499 8、0.495 6和0.493 0 m/s。由上述分析结果可得,即使网格在3个方向上均加密为原来的4倍,其流场的计算相对误差仍在2%以内,但其计算耗时为原网格的几十倍。由于所需分析的工况较多,考虑到计算成本,将网格数量设定为2 560。

图3 气溶胶初始沉积区域示意图Fig.3 Schematic diagram of aerosol initial deposition area
2.2 计算条件
Reeks等[7]在试验中考虑了3种气溶胶工质,即10 μm氧化铝粉末、20 μm氧化铝粉末和石墨粉末,并利用3种工质在不同气流速度条件下分别开展了20组再悬浮试验,试验工况记为run1~run20。表1列出3种工质的粒径分布和材料属性。
除上述试验参数外,表2列出GASFLOW计算所需的其他初始条件。
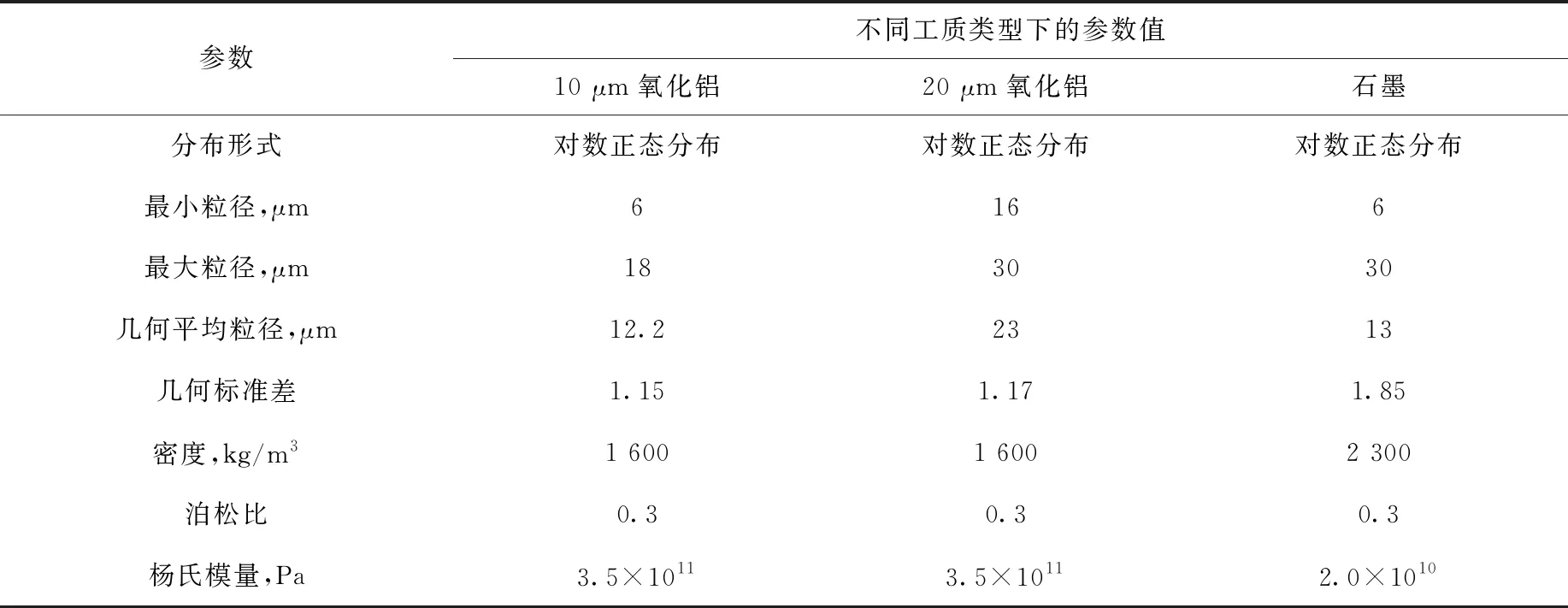
表1 3种类型气溶胶的粒径分布和材料属性Table 1 Particle size distribution and material property of three types of aerosols
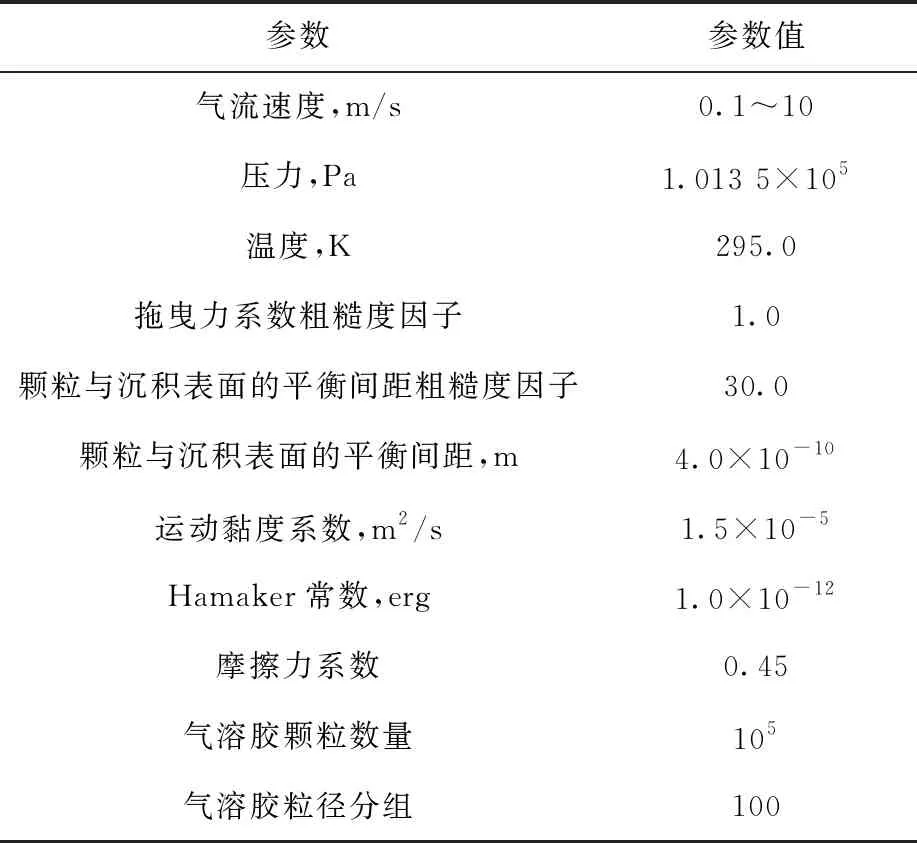
表2 GASFLOW计算初始条件Table 2 Initial calculation condition for GASFLOW
2.3 模型选取
GASFLOW中有两个湍流模型可供选择,即代数模型和k-ε模型。考虑到计算工况较多,本文研究中选用计算速度相对较快的代数模型。在计算气溶胶颗粒输运时,GASFLOW具有单向动量耦合和双向动量耦合两个模型。其中,单向动量耦合模型不考虑离散粒子相对连续流场相的影响。考虑到本文模型中的气溶胶粒子无论在体积份额还是质量份额方面与流场中气体相比都很小,离散粒子对连续流场的影响几乎可忽略不计,为节约计算成本,选择相对较为简单的单向动量耦合模型进行计算。
3 计算结果及分析
3.1 模型对比
图4示出GASFLOW与RnR模型计算结果及相关试验数据的对比。由图4可见,无论是氧化铝还是石墨工质,气溶胶滞留份额均随气流速度的增大而减小。RnR模型和GASFLOW再悬浮模型的计算结果均表现出与试验数据一致的变化趋势,相较而言,RnR模型的计算结果曲线更为平缓。为便于描述,将图4中气溶胶发生再悬浮时对应的最小气流速度定义为再悬浮最小流速,将气溶胶滞留份额为5%(即再悬浮率为95%)时对应的气流速度定义为再悬浮阈值流速。
由图4a可知,GASFLOW计算得出的再悬浮最小流速介于0.5~0.6 m/s之间,大于试验数据(约0.25 m/s)和RnR模型计算结果(约0.1 m/s)。气流速度由0.6 m/s增大至0.8 m/s时,气溶胶滞留份额迅速由0.95减小至0.27,与试验数据较为吻合。气流速度增大至1 m/s以上时,气溶胶滞留份额减小至0。GASFLOW计算得出的再悬浮阈值流速约为0.9 m/s,小于试验数据(约3.5 m/s)和RnR模型计算结果(>5 m/s)。
由图4b可知,GASFLOW计算得出的再悬浮最小流速介于0.6~0.7 m/s,大于试验数据和RnR模型计算结果(两者均小于0.08 m/s)。气流速度由0.7 m/s增大至1 m/s时,气溶胶滞留份额迅速由0.91减小至0.07,其中0.8~1 m/s之间的计算结果与试验数据符合较好。气流速度增大至2 m/s以上时,气溶胶滞留份额减小至0。GASFLOW计算得出的再悬浮阈值流速约为1 m/s,小于试验数据(约3 m/s)和RnR模型计算结果(约5 m/s)。
由图4c可知,GASFLOW计算得出的再悬浮最小流速约为0.6 m/s,大于试验数据(<3 m/s)和RnR模型计算结果(约1 m/s)。气流速度由0.7 m/s增大至2 m/s时,气溶胶滞留份额迅速由0.93减小至0.15,与试验数据较为吻合。气流速度增大至3 m/s以上时,气溶胶滞留份额减小至0。GASFLOW计算得出的再悬浮阈值流速约为2.5 m/s,小于试验数据(约5 m/s)和RnR模型计算结果(>10 m/s)。

a——10 μm氧化铝;b——20 μm氧化铝;c——石墨图4 GASFLOW与RnR模型计算结果及试验数据对比Fig.4 Comparison of calculation results of GASFLOW, RnR model and test data
综上可知,在气溶胶再悬浮的主要阶段,GASFLOW的分析结果与试验数据符合较好,可较好地模拟气溶胶再悬浮行为。
3.2 分析及讨论
综合图4的分析结果可知,气流速度是影响气溶胶再悬浮的主要因素之一。当气流速度大于再悬浮阈值流速时,95%以上的气溶胶均会再次由沉积壁面悬浮到气空间中。这说明在严重事故晚期的源项评估中,若沉积表面出现高速气流的冲击,所造成的气溶胶再悬浮作用的影响是不可忽视的。
通过上述对比分析可发现,GASFLOW计算得出的再悬浮最小流速要明显大于试验数据,而RnR模型的计算结果与试验数据较为接近。这主要是由两种模型本身的原理和特性所决定的。GASFLOW中再悬浮模型属于力学平衡模型范畴,仅考虑了拖曳力的作用,同时采用了固定的黏附力计算公式(未考虑黏附力概率分布)。虽然式(9)对再悬浮的统计特性进行了一定的考虑,但其考虑的范围较窄,仅在再悬浮最小流速为(0.8~1.2)Ugpu范围内考虑了气溶胶再悬浮的概率。当再悬浮最小流速小于0.8Ugpu时,再悬浮概率为0,而再悬浮最小流速大于1.2Ugpu时,再悬浮概率为100%,这相当于设定了明显的流速阈值。对于RnR模型而言,其不仅考虑了黏附力的概率分布,且考虑了拖曳力和抬升力的共同作用。RnR模型对气溶胶再悬浮产生机理的各种因素考虑得相对较为全面,尤其是在较低气流速度的情况下(即当气流速度接近再悬浮最小流速时),对气溶胶再悬浮率的估算更为准确。
RnR模型的计算结果曲线较为平缓,计算所得的再悬浮阈值流速显著大于试验数据。在较高气流速度的情况下(即当气流速度已接近或超过再悬浮阈值流速时),RnR模型计算的滞留份额总是明显大于试验数据,这将导致对气溶胶再悬浮率的过低估计。而GASFLOW模型则显示出了相反的特性,即在上述情况下,其计算的滞留份额小于试验数据。这表明在严重事故晚期,平行沉积表面的气流速度接近或超过再悬浮阈值流速时,GASFLOW总可给出偏保守的源项估算结果。
4 结论
通过GASFLOW再悬浮模型与RnR模型分析结果及相关试验的对比研究,得出如下结论。
1) GASFLOW再悬浮模型与RnR模型的计算结果均反映出与试验数据一致的变化趋势,但存在一定差异,这是由力学平衡模型和能量累积模型不同的原理和特性所决定的。
2) 在气溶胶再悬浮的主要阶段,GASFLOW的计算结果与试验数据符合较好,可较好地模拟气溶胶再悬浮行为,为工程应用提供技术参考。
3) GASFLOW计算得出的再悬浮最小流速明显大于试验数据,RnR模型的计算结果与试验数据更为接近。在气流速度接近再悬浮最小流速的情况下,使用RnR模型计算更为准确;当气流速度接近或超过再悬浮阈值流速时,相比于RnR模型,使用GASFLOW可得到更加保守的源项估算结果。
4) 为提升计算结果的准确性,建议在GASFLOW再悬浮模型中加入对黏附力概率分布特性的考虑。考虑到在低流速情况下RnR模型给出的结果更为保守,为保证源项分析结果的保守性,建议进一步研究在GASFLOW中开发RnR模型的可行性。

