基于贝叶斯更新方法的235U热中子独立裂变产额协方差估计

王毅箴，崔梦蕾，郭 炯，邬颖杰，刘保坤，李 富

(清华大学 核能与新能源技术研究院 先进核能技术协同创新中心先进反应堆工程与安全教育部重点实验室，北京100084)

裂变产额描述了裂变产物在裂变系统发生裂变反应过程中产生的份额。根据裂变反应的进程不同，裂变产额可分为独立裂变产额和累积裂变产额。独立裂变产额描述了瞬发裂变中子释放后，在裂变产物发生衰变前各个产物产生的份额；累积裂变产额则描述了裂变产物发生长时间衰变后裂变产物的份额[1]。由于裂变过程的时间尺度小、复杂性高，所以裂变产额的测量与模拟具有较大的不确定度。目前，ENDF/B-VII.1数据库中的235U热中子裂变产额数据来自于1994年England等的评价结果[2]，该结果仅提供裂变产额各自的方差信息，不包含裂变产额间的协方差信息，导致采用基于抽样统计不确定度分析方法研究裂变产额的不确定度传递时，无法给出合理自洽的裂变产额概率分布[3]。因此，裂变产额间的协方差估计与评价工作，十分必要[4-5]。

贝叶斯更新方法广泛应用于数据同化、数据调整及模型拟合等领域。在对裂变产额协方差的研究中， Kawano等首先基于链裂变产额估计了239Pu裂变产额的协方差[6]。其次， Pigni等将Kawano等的方法应用于ENDF/B-VII.1数据库中，研究了基于累积裂变产额的独立裂变产额调整方法，但未重点研究更新后的独立裂变产额的协方差矩阵特征[7]。随后， Fiorito等研究评价了分别用链裂变产额和累积裂变产额估计独立裂变产额协方差的差异及其对传递的裂变产额不确定度的影响[8-9]。本文基于贝叶斯更新方法，利用ENDF/B-VII.1数据库中的累积裂变产额数据及独立裂变产额自身的物理约束条件，对ENDF/B-VII.1数据库中独立裂变产额的协方差进行估计，并对估计结果进行分析和讨论。

1 独立裂变产额的协方差估计方法

1.1 贝叶斯更新方法

贝叶斯更新方法(Bayesian updating method)是一种核数据调整方法，它根据核数据的新认知(新评估结果或物理约束条件)对核数据进行调整，从而保持核数据与新认知的一致性[10-11]。该调整过程是在概率空间定义下进行的，因此，核数据x先被赋予某种概率密度分布，称为先验概率密度函数p(x)。核数据的新认知信息y被同样赋予某种概率密度分布，从而计算似然值p(y|x)。根据贝叶斯定理，核数据的后验概率分布p(x|y)可表示为

(1)

后验概率分布的最大值即为核数据的最佳调整值。由式(1)可知，贝叶斯更新方法对核数据进行调整具有3个特点：

1)允许按序分级地引入不同的核数据新认知y1,y2,…,yN，这样可以避免每当有新认知产生时，对以往核数据认知的重新引入与计算，也可以方便地分级观察和研究不同新认知对核数据调整值的影响。式(1)可改写为

(2)

2)贝叶斯更新给出的核数据最佳调整值依赖于先验概率密度分布和似然函数，它们可以通过以往人们对核数据概率分布的研究结果或基于最大信息熵原理给出[10]，从而保证核数据调整的合理性。

3)由于贝叶斯更新方法是基于核数据后验概率分布进行调整的，因此，基于获得的后验概率分布，可以对核数据的高阶矩信息进行模拟或直接计算，从而可以获得核数据在新认知约束下的协方差信息。

本文基于贝叶斯更新方法对独立裂变产额进行调整，并对ENDF/B-VII.1核数据库中缺失的协方差信息进行估计。由于ENDF/B-VII.1核数据库中仅给出了独立裂变产额的均值和标准差，由最大信息熵原理可知，采用正态分布描述独立裂变产额能够得到最大信息熵，从而可以充分利用已知的不确定度信息，最小地引入人为的主观影响。同理，对累积裂变产额也同样赋予正态分布计算似然值。

(3)

(4)

其中，Yi为独立裂变产额向量，Yi∈RP×1；P为总裂变产物数目；Yc,0,Yi,0分别为ENDF/B-VII.1提供的累积裂变产额与独立裂变产额的均值；Vc,Vi,0分别为累积裂变产额和独立裂变产额的协方差矩阵，它们均为对角阵，对角元素为ENDF/B-VII.1数据库中提供的各个裂变产额的方差,Vc∈RP×P，Vi,0∈RP×P；M为累积裂变产额与独立裂变产额的线性映射矩阵。每个裂变产物核素可由其质量数A、质子数Z及其同核异能态I确定，记为(A,Z,I)。累积裂变产额与独立裂变产额之间的关系可表示为[1]

Yc(A,Z,I)=Yi(A,Z,I)+

(5)

其中，Yc(A,Z,I),Yi(A,Z,I)分别表示裂变产物核素(A,Z,I)的累积裂变产额和独立裂变产额；b(A′,Z′,I′→A,Z,I)为裂变产物核素(A′,Z′,I′)发生衰变到裂变产物(A,Z,I)的分支比。联立所有裂变产物核素的累积裂变产额计算式，根据式(5)可得

Yc=Yi+BYc

(6)

Yc=(E-B)-1Yi

(7)

Yc=MYi

(8)

其中，Yc为累积裂变产额向量，Yc∈RP×1；B为裂变产物核素之间的分支比矩阵，B∈RP×P；E为单位矩阵，E∈RP×P。

由式(1)可以得到累积裂变产额更新后的独立裂变产额的后验概率分布为

(9)

经推导可得，独立裂变产额的后验概率分布也为正态分布，只是分布参数发生了变化。因此，独立裂变产额的后验概率分布可表示为

(10)

其中，

(11)

Yi,1=Yi,0+Vi,1MTV-1(Yc,0-MYi,0)

(12)

由于正态分布均值点的邻域内具有最大概率，所以，独立裂变产额的最佳调整值即为后验概率分布的均值Yi,1。后验概率分布的协方差矩阵Vi,1，可用于研究独立裂变产额不确定度的传递。

1.2 独立裂变产额的物理约束条件

独立裂变产额应满足3个物理约束条件：

1)在忽略三元裂变的情况下，总独立裂变产额应为2.0；

2)在忽略三元裂变的情况下，各个裂变产物的质量数以其各自的独立裂变产额为权重的平均值，应为裂变系统裂变前复合核的总质量减去释放的平均瞬发中子数；

3)各个裂变产物的电荷数以其各自的独立裂变产额为权重的平均值，应与裂变系统的总电荷数相等。

由于本文依据的ENDF/B-VII.1数据库中未提供H，He, Li, Be, B, C, N, Ne, Ti等轻核素的相关数据[12]，所以，本文分析中均忽略三元裂变。

总裂变产额维持二裂变的约束条件，采用正态分布计算似然值，则

p(Yi|Ytot,Yc,0)∝p(Ytot|Yi,Yc,0)p(Yi|Yc,0)∝

(13)

经推导，引入二裂变守恒后的独立裂变产额后验概率分布p(Yi|Ytot,Yc,0)，可化为正态分布形式，即

(14)

其中，

(15)

(16)

其中，Ytot为总独立裂变产额；σ2为总裂变产额的求和精度，本文取σ2=10-5；U为单位向量，U∈RP×1。

同理，引入裂变系统总质量数守恒约束条件，则

p(Yi│Atot,Ytot,Yc,0)∝p(Atot│Yi,Ytot,Yc,0)·

(17)

p(Yi│Atot,Ytot,Yc,0)∝

(18)

(19)

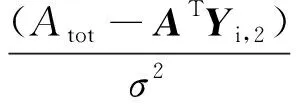
(20)

其中，Atot为裂变系统总质量数，该值可通过各个裂变核素的质量数以其ENDF/B-VII.1数据库中提供的独立裂变产额加权平均给出；A为各个裂变核素的质量数向量，A∈RP×1。

引入裂变系统的总电荷数守恒约束条件，则

p(Yi│Ztot,Atot,Ytot,Yc,0)∝p(Ztot│Yi,Atot,Ytot,Yc,0)·

(21)

p(Yi│Ztot,Atot,Ytot,Yc,0)∝

(22)

(23)

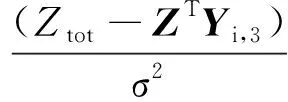
(24)

其中，Ztot为裂变系统总电荷数，该值可通过各个裂变核素的电荷数以其ENDF/B-VII.1数据库中提供的独立裂变裂变产额加权平均给出；Z为各个裂变核素的电荷数向量，Z∈RP×1。

最终得到的独立裂变产额的后验概率分布p(Yi│Ztot,Atot,Ytot,Yc,0)，能够给出独立裂变产额在累积裂变产额更新及自身的物理约束下的最佳调整值Yi,4及合理估计的协方差矩阵Vi,4。利用Yi,4和Vi,4进行独立裂变产额抽样，能够获得符合独立裂变物理约束条件且累积裂变产额一致的独立裂变产额样本数据，为后续开展不确定度传递研究提供基础。

2 估计结果

2.1 独立裂变产额调整结果与讨论

独立裂变产额的调整结果，如图1所示。其中，蓝色点代表ENDF/B-VII.1数据库中提供的235U热中子裂变的独立裂变产额，即先验独立裂变产额；橙色点代表经过贝叶斯更新后的独立裂变产额最佳调整值Yi,4，即后验独立裂变产额的均值。为方便比较分析，纵轴给出的是独立裂变质量产额Yi,m，即按质量数对裂变核素分组，并对每个质量组内核素的独立裂变产额求和的结果。由图1可见，独立裂变质量产额调整较大的核素在曲线的两峰处，对应质量数分别为80～110和130～150。这是由于两峰处裂变产物累积裂变产额的测量不确定度较小，累积裂变产额较其他位置核素的累积裂变产额更为准确，通过贝叶斯更新方法对两峰处裂变产物的独立裂变产额调整时，调整效果较为明显。

图1 独立裂变产额的调整结果Fig.1 Independent fission yields adjustment results

为了分析贝叶斯更新调整后的独立裂变产额Yi,4与ENDF/B-VII.1数据库提供的累积裂变产额评价值Yc，0的一致性，根据式(8)，分别利用先验独立裂变产额Yi，0与后验独立裂变产额Yi,4计算对应的累积裂变产额，并记为先验累积裂变产额计算值与后验累积裂变产额计算值。为方便分析，将累积裂变产额按照质量数进行分组求和，得到先验累积裂变质量产额与后验累积裂变质量产额计算值。然后分别计算它们与ENDF/B-VII.1数据库中提供的累积裂变产额评价值之比r(Yc,m)，得到r(Yc,m)随质量数A的分布曲线，如图2所示。

由图2可见，用后验独立裂变产额计算的累积裂变产额的估计不确定度在20%以内，与用先验独立裂变产额计算的累积裂变产额的估计不确定度相比减少约30%，提高了ENDF/B-VII.1独立裂变产额与累积裂变产额的一致性。对质量数为110～130的核素，更新后的估计不确定度有所放大，这是由于这些核素的累积裂变产额的先验计算结果与ENDF/B-VII.1数据库提供的评价值之间的偏差较大造成的。为表征先验累积裂变产额计算值与ENDF/B-VII.1数据库提供的累积裂变产额评价值的一致性，定义一致性因子H为

(25)

其中，NA为质量链A中裂变产物核素的数目；Yc,n为质量链A中裂变产物n先验累积裂变产额计算值；Yc,0,n为质量链A中ENDF/B-VII.1提供的裂变产物n累积裂变产额评价值；σc,0,n为ENDF/B-VII.1提供的裂变产物n累积裂变产额的标准偏差[13]。H越大，表示计算值与评价值之间的一致性越弱。图3对比了先验累积裂变质量产额计算值与ENDF/B-VII.1数据库中评价值的一致性。由图3可见，质量数为110～130和80～90核素的一致性因子H较其周围核素的H值大，具有较弱的一致性，这种较弱的一致性影响了贝叶斯更新的独立裂变产额调整结果。由于这些核素的独立裂变产额较小(位于产额分布曲线上两峰之间的低谷处)，因此，这些核素的独立裂变产额可能需要在未来的评价数据库中重新评估。

图3 先验累积裂变质量产额计算值与ENDF/B-VII.1数据库中评价值的一致性对比Fig.3 Prior calculated cumulative fission yields consistencycomparison with ENDF/B-VII.1 evaluations

图4给出了后验与先验独立裂变产额标准偏差的比值r(σ)随质量数A及电荷数Z的分布。由图4可见，多数裂变产物独立裂变产额的不确定度经过更新后有所减小，约为更新前的70%，而且位于两峰处的核素，独立裂变产额不确定度减小的幅度较大，约为更新前的20%。这是由于随着累积裂变产额评价值及其引入的不确定度的减小，且经过独立裂变产额物理约束条件的限制和似然函数的加权调整，独立裂变产额的后验概率分布会在最佳调整值附近聚集更多，从而使后验概率分布函数更加尖锐，标准偏差更小。

图4 后验与先验独立裂变产额标准偏差的比值r(σ)随质量数A及电荷数Z的分布Fig.4 Independent fission yields posterior to priorstandard deviation ratios r(σ) distribution againstmass number A and charge number Z

2.2 独立裂变产额相关性估计结果与讨论

随着累积裂变产额测量值及独立裂变产额物理约束条件的引入，独立裂变产额后验协方差矩阵会不断发生变化。图5给出了不同更新步骤下独立裂变产额相关系数矩阵的变化过程。本文对裂变产物按照质量数大小进行分组并降序排列，在每个质量数分组内按照裂变产物的电荷数大小升序排列。

由图5可见，相关系数呈团簇状出现在主对角线附近，这是由于累积裂变产额和独立裂变产额之间是通过裂变产物的放射性衰变相联系的，相关性主要出现在有放射性衰变联系的核素之间。随着二裂变约束的引入，可以看到图中Vi,2在相距较远的核素位置处产生了相关性。而随着裂变系统的质量数和电荷数守恒的引入，更多的相关性被引入到独立裂变产额的协方差矩阵中。

(a)Vi,1:p(Yi|Yc,0)

(b)Vi,2:p(Yi|Ytot,Yc,0)

(c)Vi,3:p(Yi|Atot,Ytot,Yc,0)

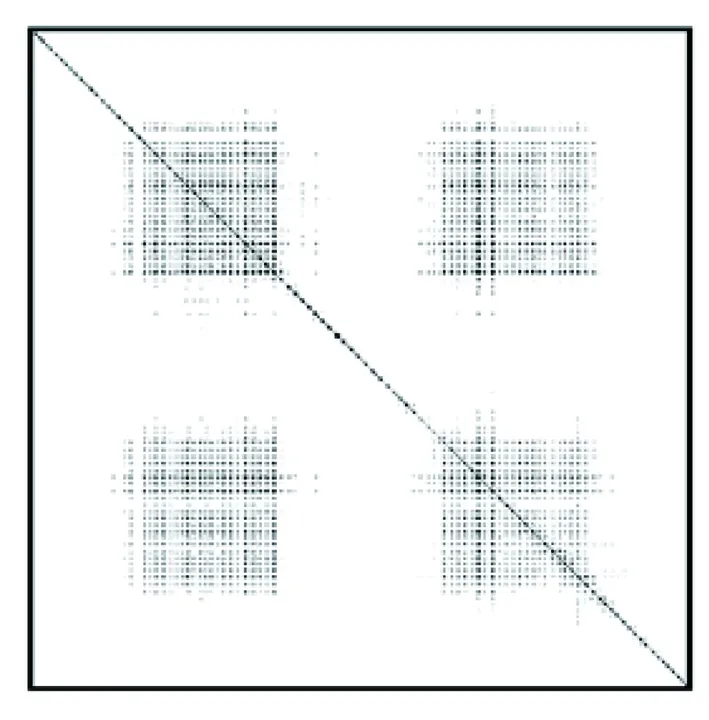
(d)Vi,4:p(Yi|Ztot,Atot,Ytot,Yc,0)

图6为图5中的Vi,4的局部放大图。其中，红色点代表正相关性系数，黑色点代表负相关性系数。由图6可见，在主对角线附近呈团簇状出现的多为负相关性系数，即由裂变产物衰变引起的核素间的相关性多为负相关；而在主对角线以外由独立裂变产额的物理约束引起的相关性则多为正相关。图7为图6左侧矩阵的下三角元素的相关系数散点图。由图7可见，贝叶斯更新方法得到的独立裂变产额之间的相关性系数多为负相关，且多数的相关性较弱，相关系数小于0.25。少数核素之间存在较强的负相关性，极少数核素之间存在较强的正相关性。

图6 相关系数矩阵Vi,4的局部放大图Fig.6 Correlation matrix of independentfission yields Vi,4 with local zoom-in view

图7 相关系数矩阵Vi,4 下三角元素散点图Fig.7 Scatter plot of lower triangle elements in correlation matrix Vi,4

近年来，国外虽然已经开展了很多基于实验链产额和累积裂变产额数据更新独立裂变产额和协方差数据的研究工作，但是，目前ENDF/B-VII.1数据库还未提供独立裂变产额的协方差数据。文献[14]中利用本文研究的独立裂变产额的协方差数据，研究了球床式高温气冷堆裂变产额的不确定度传递及独立裂变产额不确定度对堆芯平衡态下有效增殖因子和核素浓度不确定度的贡献，结果表明，有效增殖因子的相对不确定度约为2.44×10-4(燃耗为90 GW·d·t-1)，该结果和REBUS基准题中单一燃料棒栅元的相应评价结果6.0×10-4(燃耗为54 GW·d·t-1)较为接近[9]，说明本文的评估工作是合理的。

3 结论

本文基于贝叶斯更新方法，分级逐步将ENDF/B-VII.1数据库提供的累积裂变产额测量数据及独立裂变产额服从的二裂变守恒、裂变系统质量数守恒和电荷数守恒等条件引入协方差估计过程中，对ENDF/B-VII.1数据库中235U热中子裂变的独立裂变产额协方差进行了估计。结果表明，与贝叶斯更新前相比，更新后多数核素独立裂变产额的不确定度均出现了不同程度的减小，不确定度约减少了30%。多数核素的独立裂变产额之间为负相关，且相关性较弱，极少数核素的独立裂变产额之间存在较强的正相关。

本文研究是进一步开展独立裂变产额不确定度传递研究工作的基础，未来将基于本文估计的独立裂变产额协方差矩阵，研究裂变产额不确定度对反应堆燃耗及衰变热不确定度的贡献。