后屈曲预压缩技术在飞机舵机系统中的应用

朱闯锋

(上海飞机设计研究院, 上海 201210)

随着航空航天技术的不断进步,飞行器的智能化与微型化已成为未来发展的重要趋势[1]。由压电陶瓷材料制成的压电双晶片具有质量轻、结构简单且无电磁干扰等诸多优点,被大多数中外研究者们认为是飞机尤其是小型飞机驱动器的理想元件。为了克服双晶片输出位移小的缺陷,中外学者在如何提高驱动器输出能力方面做了很多研究。1997年,美国宾夕法尼亚州立大学航空工程系声学与振动中心的Lesieutre等[2]提出了后屈曲预压缩(post-buckling pre-compression,PBP)的概念,通过对压电双晶片施加轴向预压力来减小其横向刚度,进而增大驱动器的机电耦合系数,理论上当轴向预压力达到一阶屈曲临界载荷时,压电双晶片的机电耦合系数可以达到1[3]。针对这一理论,中外学者开展了一系列的试验研究工作[4-6],并将其应用于多种飞行器舵机的设计当中,取得了一定的成果[7-9]。

舵机作为飞行器的主要执行机构,其特性很大程度上决定了飞控系统的性能[10-12],因此,有必要对舵机在飞行器工作下的负载输出特性进行研究。现基于有限单元法建立PBP压电舵机的刚柔耦合动力学模型,并利用Fluent软件将某翼型在低速下的气动参数进行求解,并将计算结果代入舵机的动力学方程,对舵机在特定马赫数下由舵偏角变化导致的负载力矩改变时的输出特性进行分析,从而为双晶片舵机的优化设计与性能分析提供一定理论基础。

1 压电舵机输出特性

1.1 压电舵机的驱动方式

压电双晶片为由上、下两层压电层与中间的基体层组成的压电复合梁,如图1所示,其上、下两片压电陶瓷的极化方式相同,上端压电陶瓷的上表面与下端压电陶瓷的下表面均设置有电极,通过将基体层接地,并在两片压电陶瓷上交替施加一定的电压,利用压电陶瓷的逆压电效应,从而使双晶片发生弯曲变形。

基于PBP原理设计的压电驱动器,通过将双晶片简支安装于飞机舵机系统内,利用双晶片铰支端输出角位移带动飞机方向舵进行偏转,从而进行飞行姿态的调整。为了满足飞机飞行过程中对舵偏角与负载力矩的需求,在双晶片两端施加有一定的轴向预压力来减小双晶片的弯曲刚度,从而使其输出的力与位移得到放大，如图2所示。

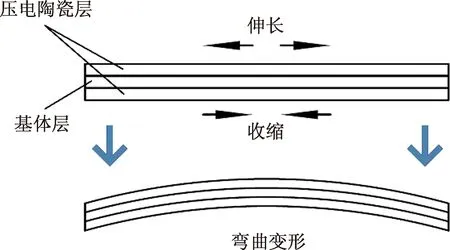
图1 压电双晶片的变形方式

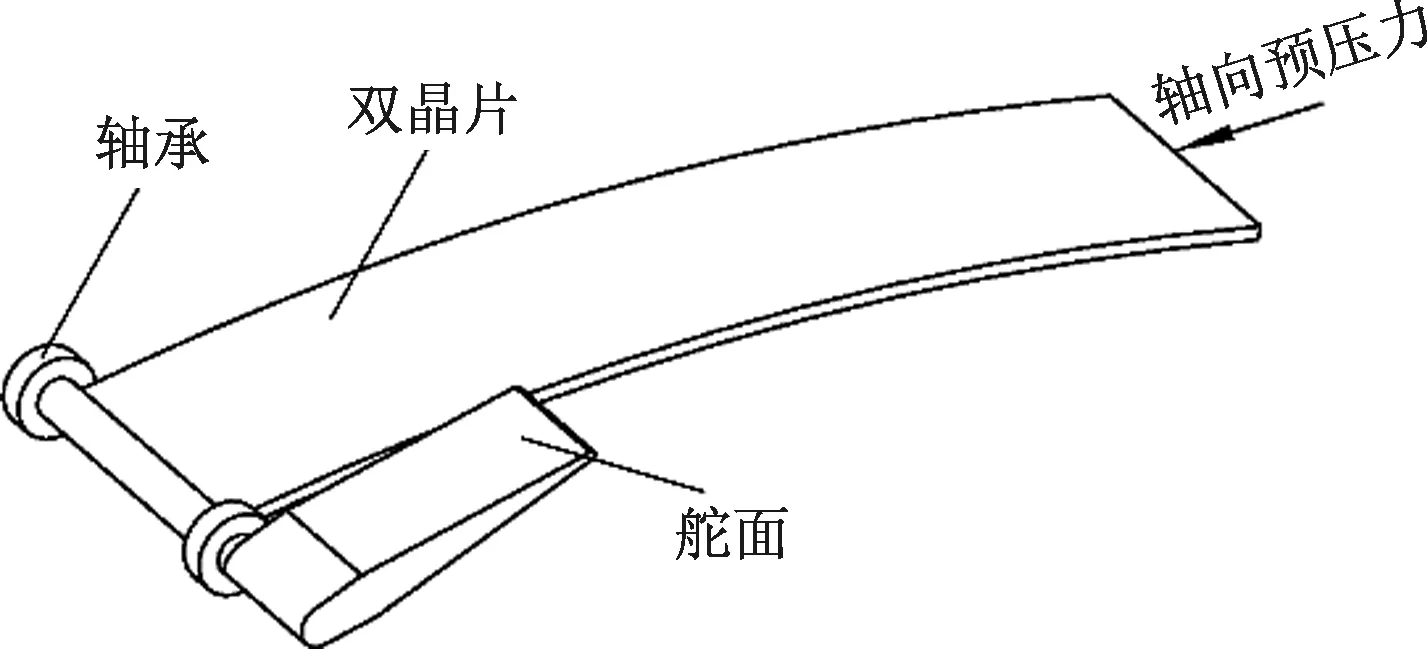
图2 PBP舵机的驱动原理

1.2 舵机动力学方程的建立

为了对压电舵机的输出特性进行研究,首先需要建立舵机的动力学方程,假设施加在PBP驱动器两端的轴向预压力为F,飞机飞行时对舵面产生的铰链力矩为M(其大小与飞机飞行马赫数以及舵偏角等参数有关),上述舵机系统可以简化为图3所示的模型。

图3 PBP舵机模型示意图

对于图3所示的舵机系统,由于压电双晶片本身具有力与电场相互耦合的作用,一般可采用能量法对其进行建模,即分别求取双晶片各层的能量进行叠加,并利用哈密顿原理得到其关于挠度的动力学方程与边界条件,但是由于轴向力F与负载力矩M的存在,通过该方法获得的动力学方程往往难以求得其解析解表达式,因此采用有限单元法对其进行求解,即将双晶片模型沿长度方向进行离散化,通过构造其单元特性矩阵并组装为整体特性矩阵,从而建立起系统的刚柔耦合动力学模型。

将沿长度方向离散化之后的双晶片挠度w用广义坐标δ与形函数N的方式表示为

w=Nδ

(1)

δ=[w0θ0wlθl]T

(2)

式中：w0与wl分别代表双晶片单元两端节点处的挠度；θ0与θl分别代表两端的转角；将双晶片的总动能、势能以及轴向力与电场力做功用广义坐标与形函数的形式表示,则双晶片单元的动能为

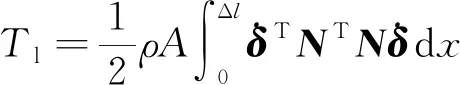
(3)

式(3)中：Tl代表双晶片单元的动能；ρA为双晶片的线密度；Δl为双晶片单元的长度。同理,双晶片单元的势能可以表示为

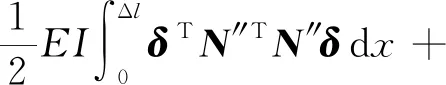
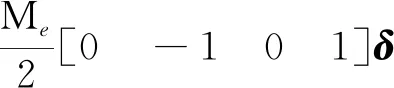
(4)

式(4)中：Ul为双晶片单元的势能；EI代表单元刚度；Me为施加在双晶片上的电压产生的等效弯矩,除此之外,电场与轴向力产生的作用可以用其对双晶片的做功WE与WF来表示,即

W=WF+2WE

(5)

将式(3)～式(5)代入拉格朗日方程,从而得到双晶片单元的动力学方程为

(6)

式(6)中：Ml与Kl分别代表单元的质量矩阵与刚度矩阵；通过将单元特性矩阵进行组装来得到总装矩阵,并根据简支的边界条件去掉总装矩阵中第1行与第1列以及倒数第2行与倒数第2列,从而得到舵机模型的总体质量矩阵M与总体刚度矩阵K,在模型中添加比例阻尼矩阵C,并将负载力矩Mj产生的作用代入方程,从而得到舵机系统的动力学方程为

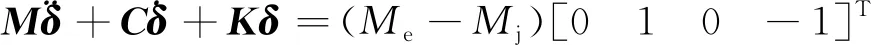
(7)

1.3 舵机负载输出特性

综合参考无人机安装尺寸的需求,建立的压电舵机数值仿真选用的双晶片尺寸参数如表1所示,其材料特性参数的选取参考文献[9]。

表1 舵机用双晶片尺寸参数

由于轴向力和电压对PBP舵机输出特性的影响在大多数文献中均有大量研究,仅对舵机系统模型在带载状态下的输出特性进行研究,将动力学方程[式(7)]中与时间相关的项去掉,从而得到舵机的静力学方程,分别选取负载力矩、电压和轴向预压力为自变量,从而得到舵机角位移输出随负载力矩、电压以及轴向力的变化关系,如图4所示。

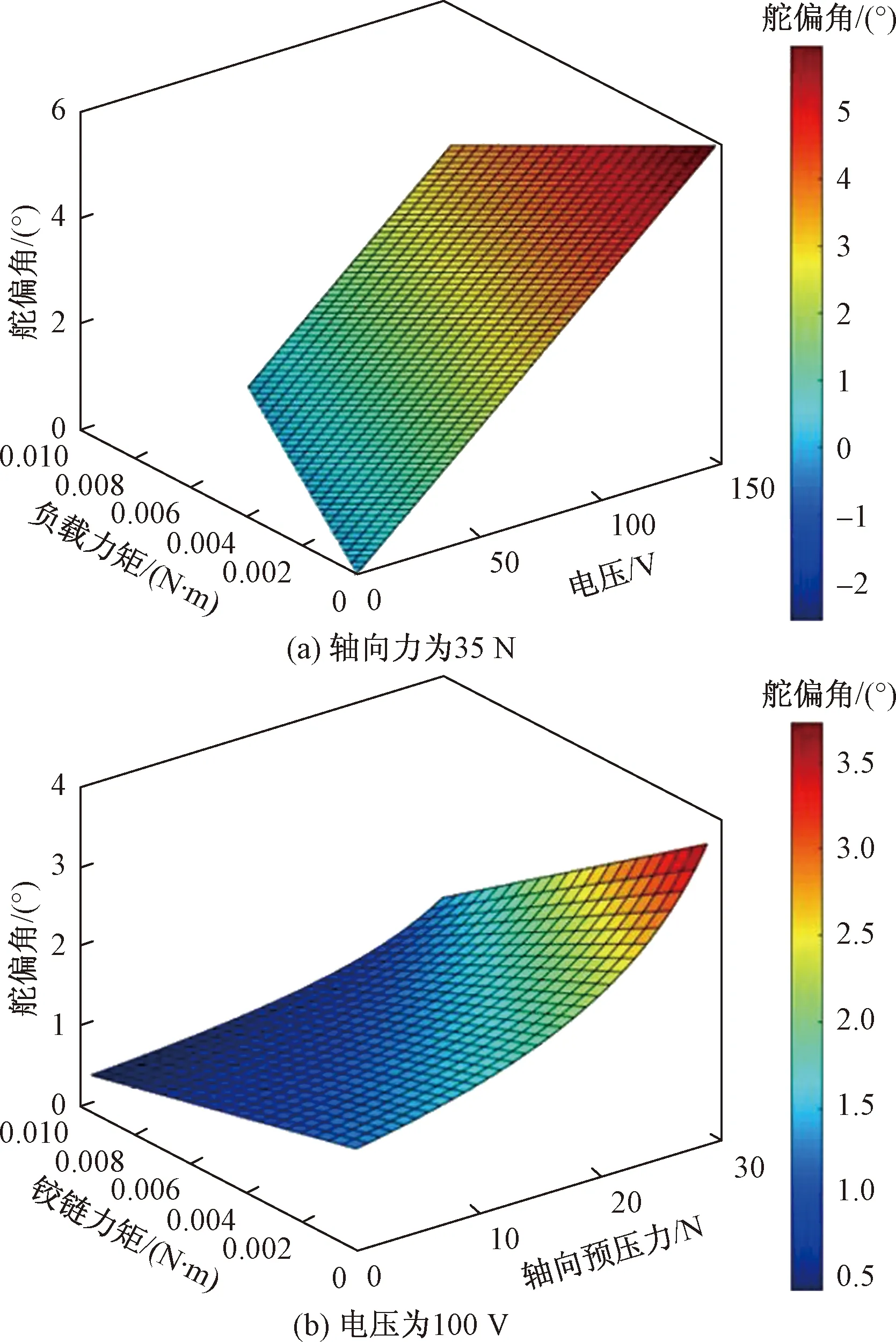
图4 舵偏角与电压、负载和轴向力的关系

从图4可以看出,舵机输出的舵偏角随着负载力矩的增大而逐渐减小,且呈线性变化的趋势,轴向力与电压的增加均可提高舵机在带载时的输出能力,但其变化趋势却不同,在负载一定的情况下,舵偏角随着电压的增加而线性增加,但随着轴向预压力的增加呈现明显的非线性增长趋势,在电压为150 V,轴向预压力为35 N的情况下,舵机的空载角位移输出可以达到6°,即使在0.006 N·m的铰链力矩下,其舵偏角仍可达到4°,该舵机的输出性能完全可以满足工作在低速下的飞机使用需求。

2 舵面气动参数计算

为了对舵机在受到气动载荷情况下的输出特性进行研究,首先对不同舵偏角下舵机受到的舵面铰链力矩进行计算,并将计算结果以插值表的形式代入动力学方程[式(5)]中,从而获得在考虑由舵偏角变化引起的铰链力矩变化时舵机的输出特性。

参考无人机的飞行速度一般在10～20 m/s,因此选择某低速翼型作为舵机使用的参考翼型,弦长设置为30 mm,利用Ansys Fluent软件对翼型进行气动仿真计算,采用O型拓扑结构对模型进行结构化网格的划分,计算域的外边界为直径1 m的压力远场。

在压力远场中设置风速为20 m/s,采用SSTk-w模型分别对1°～6°攻角下翼型的气动力系数进行计算,结果云图如图5所示。

假设舵机的转轴中心线经过翼片的几何中心,选取翼型展长为30 mm,分别提取计算收敛后不同舵偏角下翼型相对转轴中心的气动力矩系数,通过计算得到舵机在不同舵偏角下受到的铰链力矩,其结果如图6所示。

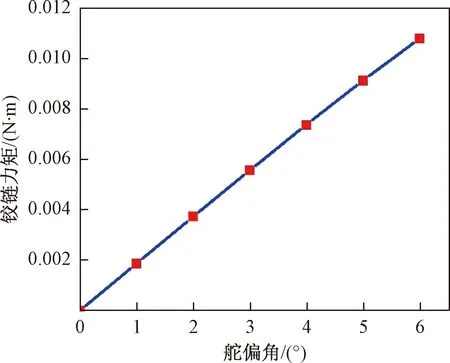
图6 铰链力矩随舵偏角变化关系

从图6中可以看出,在马赫数较小的情况下,舵机受到的铰链力矩随舵偏角的增加而增加,且基本成线性变化。舵偏角在整个变化过程中,舵机受到的铰链力矩基本在10-3数量级上,当舵偏角达到6°时,舵机受到的铰链力矩约为0.011 N·m,结合前面的分析可以看出,基于PBP原理设计的压电舵机完全满足该飞机的应用需求。

3 压电舵机在风载下的输出特性

当风速一定的情况下,舵机承受的负载力矩和其舵偏角之间有着一定的关系,为了对承受气动载荷时的压电舵机输出特性进行研究,将前面利用Ansys Fluent软件计算得到的铰链力矩结果代入舵机的动力学方程[式(7)]中,去掉方程中与时间相关的项,从而得到以20 m/s的速度飞行时舵机的角位移输出特性。

图7给出了不同轴向力下舵偏角随电压的变化关系,计算中加入了风速为20 m/s时施加在舵机上的铰链力矩,从图7中可以看出,舵偏角随电压的变化曲线几乎呈线性增长趋势,且随着轴向预压力的增加而逐渐增加,增加轴向预压力可以明显提高舵机的机电耦合效率,从而使舵机在低电压下实现大角度的输出。

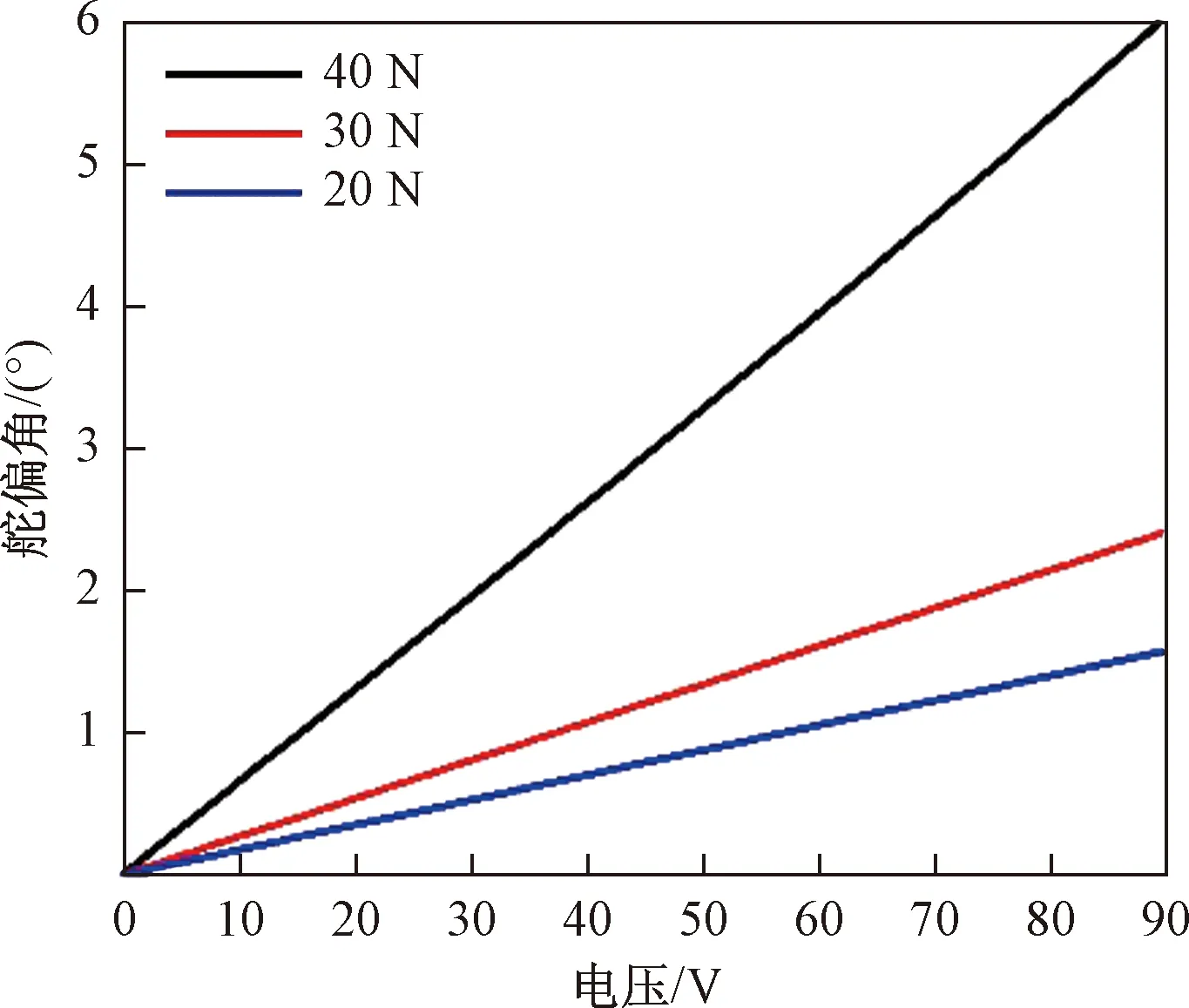
图7 舵偏角随电压的变化关系

4 结论

结合分析力学、结构动力学与有限单元法建立了可用于小型飞机的PBP压电舵机刚柔耦合动力学模型,对舵机的负载输出特性进行了分析。同时利用Ansys Fluent软件对低速翼型NACA0012在不同舵偏角下的气动参数进行了仿真计算,并将计算结果导入建立的舵机模型,对在低马赫数下该翼型应用于小型飞机舵机系统的可行性进行了验证。结果表明,气动载荷的作用会减小舵机的静态输出能力,但轴向力的增加可以显著提高舵机系统的机电耦合效率,从而弥补了较大转角下铰链力矩对舵机角位移输出产生的负面影响,使得该PBP舵机完全可以满足小型飞机的应用需求。