弱交流电网下不同位置的直驱风机对次同步振荡特性影响的比较分析

赵书强， 赵质淼， 邵冰冰

(华北电力大学 河北省分布式储能与微网重点实验室，河北 保定 071003)

0 引 言

在新能源开发的浪潮中，风电凭借其可再生、装机规模灵活以及运行维护成本低的优势，在国内外迅速发展[1-2]。据统计，2019年全球新增风电装机容量为60.4 GW[3]，未来风力发电有望成为主力发电能源[4]。永磁直驱风机(Permanent Magnet Synchronous Generator, PSMG)作为主流的风力发电机之一，没有励磁控制系统以及变速箱等结构，通过全功率变流器接入电网[5]。当电网出现故障时变流器可以将故障隔离，使PMSG具有良好的故障穿越能力和可靠性。但在实际工程中，并网风机接入线路阻抗较大的弱交流电网，系统稳定性相对较差[6]。如2015年7月1日，新疆发生PMSG接入无串联补偿装置交流电网的多次持续SSO(Sub-Synchronous Oscillation, SSO)现象，导致数百公里外的火电机组保护装置动作[7]。因此，风电场与弱交流电网交互作用引起的SSO是亟待研究的问题之一[8-10]。

针对直驱风电场并入弱交流电网的SSO问题，国内外学者已取得一定的研究成果。文献[11]建立了直驱风电场并入弱交流电网的动态模型，分析了交流系统强度、风机并网台数、风机控制参数等因素对SSO特性的影响；文献[12]研究了全运行区域下，不同风速、输出功率对PMSG并入弱交流电网系统SSO特性的影响；文献[13]采用阻抗法分析了电网强度、控制器参数等对直驱风机并网系统SSO特性的影响；文献[14]采用导纳特性分析法，研究了前置滤波带宽、电流内环、电压外环等因素对直驱风机并网系统SSO特性的影响；文献[15]建立了直驱风电场接入交流电网的等值模型，分析了交流电网强弱、风机功率、控制参数以及动态无功补偿设备等因素对SSO特性的影响；文献[16]建立了考虑锁相环(phase locked loop,PLL)动态特性的单台直驱风机并网动态模型，给出了直驱风机引发SSO的判据，并分析了PLL系数、电流内环系数及电网强度对SSO特性的影响。文献[17]在双馈风机经串补并网的场景下，对比了单机与多机等值模型对SSO特性的影响，而本文的研究场景是两直驱风机并入弱交流电网。且文献[17]侧重点在于对比单机和多机等值模型的差异，而本文侧重点在于两机等值模型下，远端子风电场和近端子风电场对SSO特性影响程度的对比分析，可以在一定程度上让施工人员了解风电场并网距离远近对SSO特性的影响。

由以上分析可知，现阶段对直驱风电场并入弱交流电网系统SSO问题的研究大多采用单机等值模型。但是，采用单机等值模型不能考虑处于不同位置的风机由于风速、开机数配比、短路比的不同对系统SSO的影响，不能对比分析出哪个位置的子风电场对整个系统SSO特性影响更大。因此，研究不同位置多机等值模型的直驱风电场并网系统SSO问题具有重要的实际意义。

本文将两个不同位置的直驱风电场等效为两台风机，建立两台PMSG并网系统的小信号数学模型，通过特征值分析和时域仿真分析两个风电场风速、开机数配比不同以及短路比对整个系统SSO的影响。此外，分析对比了不同位置的两子风电场对整个系统SSO特性影响程度。

1 系统建模

本文研究不同位置直驱风机并网的SSO问题，首先建立系统模型。由于不同地理位置的风速不同，所以单台风机等值整个风电场不够严谨。本文分别用一台风机等效一个子风电场，这些子风电场通过汇流母线与整个风电场相连[18]。因此，本文通过两个风机PMSG1、PMSG2分别等效远端和近端两个小风电场，PMSG1、PMSG2经升压变升压至110 kV后并入交流电网，如图1所示。图1中Rgg、Lgg、Cgg分别为并网线路的电阻、电感以及电容。e表示整个风电场的公共连接点。Rg1、Lg1、Cg1分别为PMSG1与汇流母线之间的电阻、电感、电容，Rg2、Lg2、Cg2分别为PMSG2与汇流母线之间的电阻、电感、电容。为了模拟两风机距离汇流母线的远近，忽略电阻，Lg1为Lg2的两倍。

在实际工程中，由于风能发达地区和负荷中心呈逆向分布，西部绿色的风电需要通过长距离输电线路输送至东部负荷中心[19]。这种情况下，电网的阻抗不可忽略，发电系统和电网之间的联系相对较弱。本文研究弱交流电网下直驱风电场的SSO问题。一般以短路比为3界定强弱电网，短路比小于3的电网为弱交流电网[19]。据此，本文所建立的模型短路比为2.4，从而模拟PMSG并入弱交流电网的场景。

图1 两台直驱风机并入弱交流电网模型Fig.1 Double-PMSGs merged into a weak AC grid model

2 两台直驱风机并网系统小信号模型

本文的直驱风机并网系统小信号模型主要包括发电机转子运动方程、直驱永磁同步发电机模型、背靠背换流器模型、风电输电线路模型、PLL模型以及风电并网线路模型。

2.1 发电机转子运动方程

直驱风机轴系自然扭转频率较低，所以不易发生轴系扭振问题[21]，所以本文研究的SSO问题与轴系无关。相对于多质量块模型，采用单质量块模型建模工作量更小，并且足够反映本文研究的SSO问题。发电机转子运动方程动态方程为

(1)

式中：J为直驱风机的总转动惯量；ω为风机转速；TM风机的机械转矩。

TM=0.5ρSCpv3/ω

(2)

式中：ρ为空气密度；S为风力机的扫风面积；Cp为风能利用系数；v为所处地区风速。控制d轴电流为0，Te的表达式为

Te=1.5npiqsψf

(3)

式中：np为永磁电机极对数；iqs为定子电流在q轴上的分量；ψf为磁通；Te为发电机的电磁转矩。

2.2 直驱永磁同步机的动态模型

永磁发电机定子绕组采用电动机惯例，忽略磁滞损耗和涡流，永磁体磁场与d轴的相位一致，结合图1系统结构。可得d、q同步旋转坐标系下PMSG的动态数学模型为

(4)

式中：Ls、Rs分别为定子电感和电阻；ωs为永磁发电机的电转速；uds、uqs以及ids、iqs分别为定子电压和电流的d、q轴分量。

2.3 背靠背换流器的动态模型

机侧换流器(Machine-side Converter, MSC)控制发电机的有功功率，实现最大功率跟踪，同时控制d轴电流为 0，使发电机的损耗最小；网侧换流(Grid-side Converter, GSC)采用定直流电压控制和并网无功功率控制。背靠背换流器控制框图见图2。

图2 背靠背换流器控制框图Fig.2 Control block diagram of back-to-back converter

由图2可知MSC、GSC动态方程为

(5)

(6)

式中：uDC为背靠背换流器直流侧电容电压；idsref为定子电流d轴分量的参考值；iqsref为定子电流q轴分量的参考值；ωsref为永磁发电机转速的参考值；Δx1为MSC定d轴电流；Δx2、Δx3为MSC外环、内环定转速；Δx4、Δx5为GSC外环、内环定直流电压；Δx6为GSC定q轴电流；idg、iqg为GSC出口d、q轴电流；uDC、uDCref分别为直流电容电压及其参考值。

2.4 风机输电线路动态模型

风机输电线路为风机经过变压器之后的线路，两个风机通过输电线路连接只整个系统的汇流母线。忽略变压器内阻抗，输电线路的动态方程如式(7)所示。

(7)

式中：ωg为工频角速度；L为滤波电感；Lg1与Lg2分别为两风机输电线路电感；k1为风机出口变压器变比；udt、uqt为GSC出口d、q轴电压；udg、uqg分别为风机出口处电压d、q轴分量；idl、iql分别为风机输电线路的d、q轴电流；ed、eq分别为公共连接点电压的d、q轴分量。

2.5 PLL的动态模型

PLL的控制框图如图3所示。在PMSG的GSC模型中，以节点电压ug为基准设定d-q旋转坐标系，ug的q轴分量作为PLL的输入。

图3 PLL控制框图Fig.3 Block diagram of PLL control

由图3可知PLL的动态方程为

(8)

式中：xa和xb为风机PLL的状态变量。图中kpp为PLL中的比例系数；kii为PLL中的积分系数；ω0为基准角速度。

2.6 风电并网线路动态模型

并网线路为公共连接点与弱交流电网之间的线路，此部分采用RLC线路模型。

(9)

式中：idll、iqll为两个子风机并网线路d、q轴电流之和；idss、iqss为并网线路d、q轴电流。

根据以上动态模型，可推导出两台直驱风机并入弱交流电网输电系统的数学模型，经线性化可得系统的小信号模型为

(10)

式中：Δx为线性化后的状态变量；Δu为线性化后的输入变量；A为状态矩阵；B为输入矩阵。

综上所述，对于单机等值系统，每台 PMSG 发电系统的状态变量为18个(PMSG1的状态变量上标为1，PMSG2的状态变量上标为2，例如Δω1为PMSG1风机转速),另外整个系统并网线路的状态变量为4个，本文的所建立的系统模型共有40个状态变量：{Δω1、Δids1、Δiqs1、ΔuDC1、Δx11、Δx21、Δx31、Δx41、Δx51、Δx61、Δidg1、Δiqg1、Δudg1、Δuqg1、Δidl1、Δiql1、Δxa1、Δxb1、Δω2、Δids2、Δiqs2、ΔuDC2、Δx12、Δx22、Δx32、Δx42、Δx52、Δx62、Δidg2、Δiqg2、Δudg2、Δuqg2、Δidl2、Δiql2、Δxa2、Δxb2、Δed、Δeq、Δidss、Δiqss}。

3 振荡模式分析

本文采用特征值分析法对以上系统进行振荡模式分析，计算两直驱风机并网系统状态矩阵的特征值。当两台直驱风机风速均为10 m/s，开机数配比均为50%时，可得系统的主要振荡模式如表1所示。

根据表1可知，系统存在4个主要振荡模式，分别为2个中频(200～500 Hz)[22]振荡模式λ1,2、λ3,4，1个SSO模式λ5,6以及1个低频振荡模式λ7,8。中频振荡和低频振荡的特征值实部均为负值，阻尼比均为正值，说明系统在这些振荡模式下是稳定的。而SSO的特征值实部为正值，阻尼比为负值，说明系统有发生SSO的风险，因此SSO模式作为本文主要研究对象。下文将分析对比PMSG1和PMSG2，在各种因素影响下对整个系统SSO特性的影响程度大小。

表1 两台直驱风机并入弱交流电网模型主要振荡模式

4 处于不同位置的风机影响因素变化对SSO的影响

4.1 影响因素为风速

实际运行中，不同位置的地理条件存在差异，风速也会存在较大差异，所以会导致风机在实际运行时转速不同。PMSG1定义为1号风机，PMSG2定义为2号风机。通过计算在不同风速下的特征值来分析风速对系统SSO特性的影响，两台风机SSO特性随风速变化的趋势如图4所示。图4中V1代表远端风机PMSG1的风速，V2代表近端风机PMSG2的风速。根据图4(a)可以看出，在给定范围内，风速越大，特征值实部越小即系统越稳定。根据图4(b)可以看出，风速越大，振荡频率越小。

图4 两风机运行于不同风速对SSO特性的影响Fig.4 Effect of two fans operating at different wind speeds on SSO characteristics

为了比较分析不同位置风机在风速变化量相同时次同步振荡特性变化量大小，取图4(a)中边界曲线AM、AN以及图4(b)中边界曲线BP、BQ，将其投影到二维坐标系中，得到图5(a)和图5(b)。图5(a)中两条曲线分别是V1不变，V2由10 m/s下降到5 m/s以及V2不变，V1由10 m/s下降到5 m/s对应SSO特征值实部变化曲线。从图中可得PMSG1和PMSG2风速分别都由10 m/s下降到5 m/s，两台风机风速变化特征值实部都增大，但是PMSG2风速变化时特征值实部变化更大。由此可得在一定范围内，风速越大系统稳定性越好。当风速变化时，近端风机对整个系统SSO稳定性影响更大。

图5 两风机运行于不同风速对SSO特性影响对比分析Fig.5 Comparative analysis of the influence of two fans running at different wind speeds on SSO characteristics

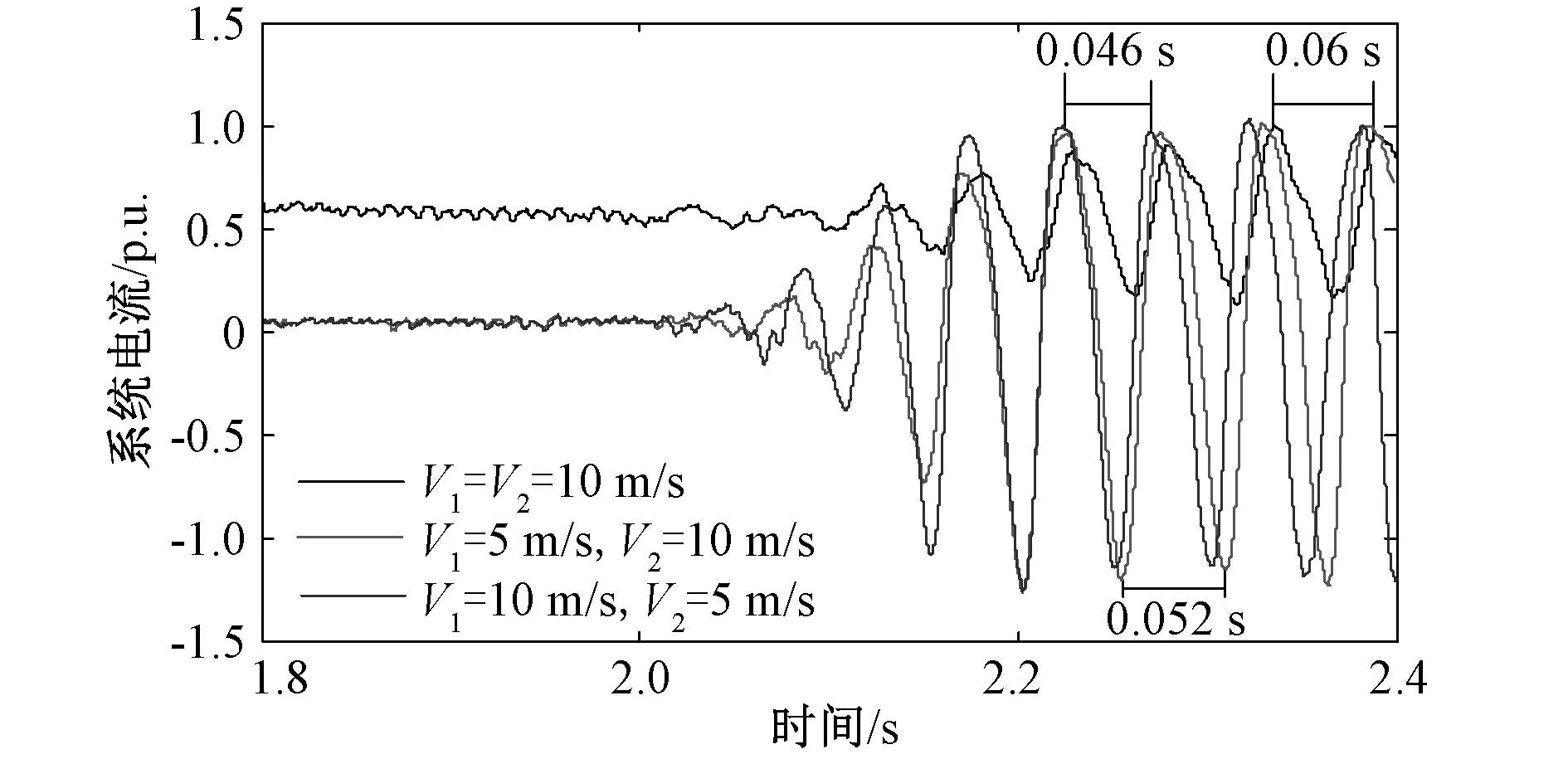
图6 两风机运行于不同风速时仿真结果Fig.6 Simulation results of two wind farms running at different wind speeds

图5(b)为两台直驱风机由于风速不同对SSO频率造成的的影响。由图5(b)可知PMSG2振荡频率随风速变化而改变的量更大，说明不同风速下近端风机对系统振荡频率的影响更大。在PSCAD/EMTDC中搭建相应的仿真模型来验证上述分析。仿真结果如图6所示，在2 s时将ki4由20变为200，引发系统振荡，从系统电流随时间的变化可以发现，图中存在三条曲线对应三种不同工况，即(1) PMSG1、PMSG2风速均为10 m/s，(2) PMSG1风速为5 m/s， PMSG2风速为10 m/s，(3) PMSG1风速为10 m/s，PMSG2风速为5 m/s。可以看出在以上三种情况下，系统均为发散的，但当有风机风速下降时，曲线明显比PMSG1和PMSG2风速相同时系统发散速度更快，说明当有风机风速下降时，都会使系统变得更加不稳定。但相较于远端风机，近端风机风速变化时系统发散速度更快，说明近端风电场对于整个系统SSO的影响比远端风电场更大。且从图6中三种情况的振荡周期得，三种情况振荡频率分别为16.7 Hz、19.2 Hz、21.7 Hz，这与图5(b)中的振荡频率基本一致。综上，仿真结果验证了特征值分析结果。

4.2 影响因素为开机数配比

在实际工程中风电场的功率大多不尽相同，所以本节将分析两子风电场开机数配比对SSO的影响。本文假设整个风电场输出功率恒定，假定1号风电场的开机数配比为k，则2号风电场的开机数配比为1-k。此时不考虑风速的影响，并假定风速相同，风机都处于最大功率跟踪状态，每个风电场接入的风机越多，输出功率越多。通过测量不同开机数配比下的特征值实部和频率来分析开机数配比对系统稳定性造成的影响。

图7(a)为特征值实部随1号风电场开机数配比变化图，由于两风电场开机数配比之和为1，1号风电场开机数配比变化时，2号风电场开机数配比也变化。计算1号风电场开机数配比变化时特征根实部的数值。从图7(a)可以看出特征值实部随着1号风电场开机数配比的增大而减小，说明远端风电场开机数配比越大，系统越稳定。图7(b)为振荡频率随1号风电场开机数配比变化图，分别计算1号风电场开机数配比变化时的振荡频率。由图7(b)可得，一定范围内，1号风电场开机数配比越大，系统振荡频率越大。

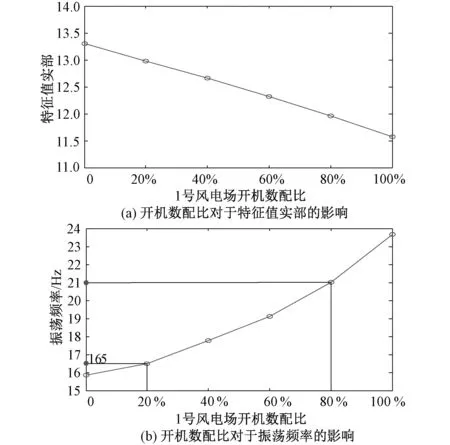
图7 两风电场开机数配比不同对SSO特性影响对比分析Fig.7 Comparative analysis of the influence of different start-up ratios of two wind farms on SSO characteristics

采用时域仿真来验证计算结果的正确性，图8为系统电流的时域仿真图像，在2 s时将ki4由20变为200，引发系统振荡。从系统电流随时间的变化可以发现，当k=80%时系统振荡的发散速度慢于k=20%时系统振荡的发散速度。说明不论1号风电场开机数配比高或低，系统都是不稳定的，但是系统的不稳定程度会随着远端风电场开机数配比的增加而减小。且从图8中的振荡周期可得，k=20%和k=80%的振荡频率分别为17.0 Hz、20.8 Hz，这与图7(b)基本一致。综上，仿真结果验证了特征值分析结果。

图8 两风电场开机数配比不同时仿真结果Fig.8 Simulation results when two wind farms have different start-up ratios

4.3 影响因素为短路比

本节研究短路比对系统SSO的影响，假设风机运行在最大功率点跟踪模式，短路比的大小代表交流电网强弱，且接入交流电网强弱通常用连接电抗值来表征[9]。本系统电容可以忽略，所以本节用输电线路电感值的变化来表征短路比的变化。输电线路电感值越大，短路比越小，交流电网强度越弱，反之输电线路电感值越小，短路比越大，交流电网强度越强[10]。图9(a)为输电线路电感值变化对整个系统特征值实部的影响。从图9(a)可以看出在Lg1减小，Lg2不变以及Lg2减小，Lg1不变这两种情况下系统特征值实部都减小，但是变化量不同。在电感减小量相同的情况下，Lg1减小，Lg2不变时，特征值实部变化更大。图9(b)为输电线路电抗值变化对整个系统振荡频率的影响。从图9(b)可以看出在电感减小量相同的情况下，Lg2减小，Lg1不变时，系统振荡频率变化更大。综上所述，输电线路电感减小即短路比增大时，系统会越稳定，近端子风电场对系统SSO特性影响更大。

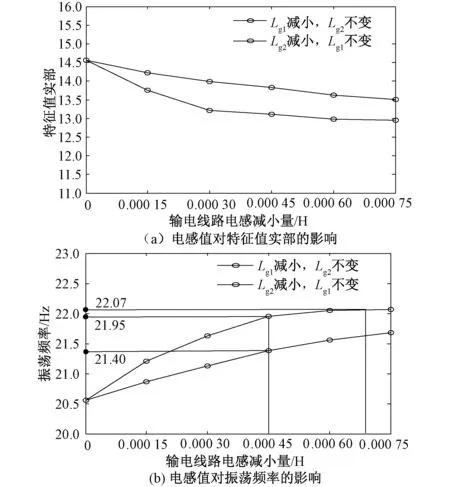
图9 两风机输电线路电感不同对SSO特性影响对比分析Fig.9 Comparative analysis of the influence of different inductances on transmission lines of two fans on SSO characteristics

图10 两风机输电线路电感不同时的仿真结果Fig.10 Simulation results of two wind turbine transmission lines with different inductances

在2 s时将ki4由20变为200，引发系统振荡。从时域仿真图10可以看出在Lg1和Lg2都减少0.000 45 H时，系统的振荡程度不同，Lg2减小时系统发散速度更慢，说明近端子风电场对SSO特性影响更大，且根据图10中振荡周期可得，Lg1减少0.000 45 H和Lg2减少0.000 45 H时振荡频率分别为21.3 Hz以及21.7 Hz，这与图9(b)基本一致。综上仿真结果验证了特征值分析结果。

除此之外，由图9可以看出当Lg2的减小量从0.000 60 H到0.000 75 H时系统的SSO特性基本不再变化，由此可得当风电场内部电感减小到一定值时，就可忽略其带来的影响。由于上文已经分析出近端风电场对系统SSO特性影响更大，且Lg2更小，所以只需研究Lg2即可。仿真图11可以看出Lg2的减小量从0.000 60 H到0.000 75 H时两条曲线基本拟合。风电场外部电感为0.01H，Lg2初始值为0.001H，减小到0.000 4 H时即可忽略其影响。综上，在忽略电阻电容的情况下，可得当风电场外部电网阻抗大于内部线路阻抗25倍时，可忽略内部线路阻抗的影响。

图11 风电场内部阻抗可忽略时的仿真结果Fig.11 Simulation results when the internal impedance of the wind farm is negligible

5 结 论

本文首先搭建两直驱风电场并入弱交流电网的等值模型，两风机分别等值两个并网距离不同的子风电场，经过特征值分析找出系统中的SSO模式。然后对系统SSO采用特征值分析法进行分析，最后用PSCAD/EMTDC时域仿真验证结果的正确性。主要结论如下：

(1)在风速影响下，并网距离不同的等值子风电场对系统稳定性影响程度不同，并网距离近的等值子风电场的影响程度高于并网距离远的等值子风电场。

(2)在整个系统输出功率之和不变的条件下，并网距离远的等值子风电场所占开机数配比越大，系统越稳定，即当所有风机输出功率相同的情况下，并网距离远的等值子风电场接入风机越多，系统越稳定。

(3)在短路比影响因素下，短路比越大系统越稳定，并网距离近的等值子风电场对系统SSO特性影响更大，且当风电场外部电网阻抗大于内部线路阻抗25倍时，可忽略内部线路阻抗对系统的影响。