采用三次谐波注入调制策略的模块化多电平换流器稳态运行特性解析分析及优化

孙海峰， 黄家晨， 马 龙

(华北电力大学 电气与电子工程学院, 河北 保定 071003)

收稿日期：2020-06-09.

基金项目：中央高校基本科研业务费面上基金项目(2019MS080).

0 引 言

模块化多电平换流器(Modular Multilevel Converter, MMC)是柔性直流输电领域中关注度较高[1-3]、应用较普遍的换流器[4-6]。与其它换流器相比，MMC具有输出电压谐波含量低、易于扩展、能量传输过程能量损耗小等特点[7-9]。受限于IGBT器件的过流能力，较弱的过流能力降低了系统的安全性，并使得系统的故障穿越能力降低。注入三次谐波能较好的改善这一系列问题：(1)注入三次谐波使得直流电压利用率提高[10-11]，从而使得MMC输出最大交流电压提高，进而降低系统稳态时和暂态时功率器件承受的电流应力及产生的损耗；(2)注入三次谐波也能降低子模块电容电压纹波[12-15]，进而降低功率半导体器件承受的电压应力。

注入三次谐波后，MMC相应的稳态运行特性也会发生相应的改变，将会向交流侧输出大量五次谐波和七次谐波。不少学者做了大量工作，文献[16]在不考虑三次谐波注入的情况下，分析了桥臂环流和子模块电容电压的谐波成分。文献[17]建立了采用三次谐波注入策略MMC的16阶相量动态模型。文献[18]分析了不同接地方式下，三次谐波注入策略的适用性，并对桥臂电流、子模块电容电压进行了分析，但并未给出桥臂电压的解析式。文献[19]分析了环流抑制策略的投入和切除对采用三次谐波注入策略的MMC稳态运行特性的影响，得出了三次谐波注入策略会在桥臂电压上产生额外的五次、七次谐波分量，并导致交流侧出现大量五、七次电压谐波的结论，这将会危害电力系统的稳定运行，但并未对其进行解析。

本文利用开关函数，分析了三次谐波注入对MMC稳态运行特性的影响。考虑到MMC在稳态运行时，子模块电容电压直流分量与额定电压相比有一定误差，但相对子模块电容电压基波分量和各次谐波分量而言，其所占比重较大，因此本文对其进行了理论推导。推导了桥臂电压的各次谐波分量，并进行了理论分析。因环流抑制器产生的调制函数二倍频分量幅值较小，故忽略了与其有关的项，得到了桥臂电压五次、七次谐波分量、电容电压直流的分量的理论解析式。考虑到桥臂电压五次、七次谐波分量将会输出到交流侧，将对交流系统产生危害，因此对三次谐波注入策略进行了改进。最后，通过PSCAD仿真验证了所提解析式的正确性及优化策略的有效性。

1 模块化多电平换流器的三次谐波注入策略

子模块SM具体结构图如图1所示，图2为MMC的整体结构图。MMC有3个上桥臂和3个下桥臂，共6个桥臂，每桥臂串联一个电抗L;一个上桥臂和一个下桥臂构成一相，MMC共有3相。

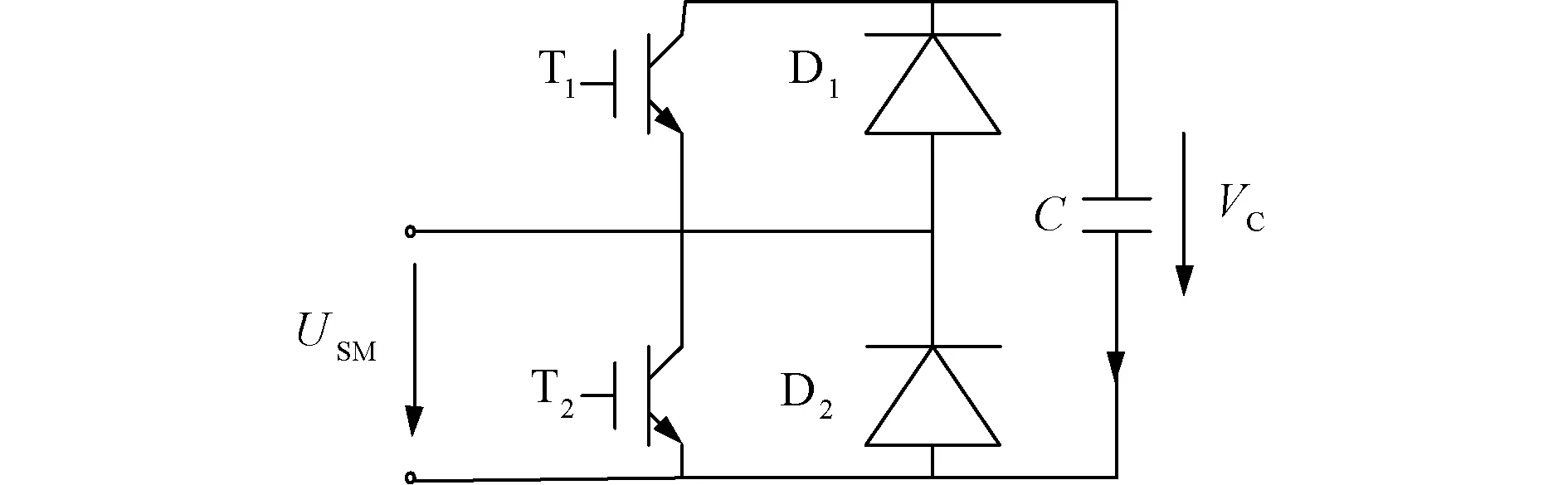
图1 子模块结构图Fig.1 Sub-module structure diagram

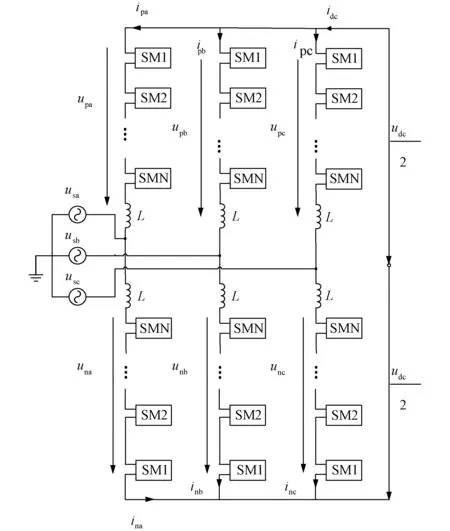
图2 单端MMC整体结构图Fig.2 Overall structure of single-ended MMC

图2中，upj、unj、ipj、inj分别表示上下桥臂电压、电流(p表示上桥臂，n表示下桥臂，j=a,b,c表示A、B、C 三相)；udc表示MMC直流侧直流电压。

MMC在稳态运行时，通过控制一相上下桥臂投入子模块总数N来保持直流侧电压稳定，同时MMC通过调整每相上下桥臂投入子模块数量得到所需的输出电压。

子模块包含2个IGBT和2个二极管，其中二极管分别与IGBT反并联。MMC正常运行时，子模块包含投入和切除2个状态。当T1接收开通信号、T2接收关断信号时，电流流经电容器，子模块投入，Usm=VC；当T2接收开通信号、T1接收关断信号时，电流经子模块下半部分直接流出，不流经电容器，子模块切除，Usm=0。

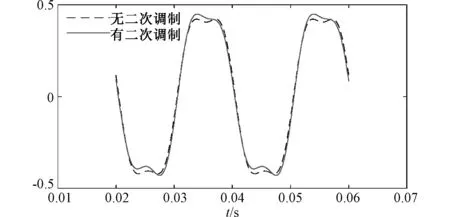
图3 调制波对比图Fig.3 Modulated wave comparison chart

2 注入三次谐波的模块化多电平换流器稳态运行特性解析

为简化分析，本文推导基于以下假设：

(1)稳态运行时，同一桥臂子模块电容电压完全相同；

(2)MMC中子模块各参数完全相同，且在运行前已完成预充电，电压为udc/N。

以A相为例进行分析，B相和C相可类比推得。

由于MMC各桥臂均由N个子模块和一个电感L构成，各桥臂参数完全相同，交流侧基波电流在上下桥臂均分；MMC每相由上下2个桥臂组成，各相参数完全相同，A、B、C三相均分直流侧电流直流分量，每相桥臂电流直流分量为直流侧电流直流分量的三分之一。

根据文献[16,20]中分析可知，桥臂环流仅包含偶次谐波分量，主要成分为二次谐波分量，且一相上下桥臂环流各次谐波分量幅值和相角大小相等。

在MMC实际稳态运行中，MMC桥臂环流中四次及以上谐波电流幅值较小，可忽略不计，并假设二次环流被充分抑制。

环流抑制模块会在桥臂电压调制函数中添加一个二倍频分量，定义下列等式：

M3cos(3y+M33)]

M3cos(3y+M33)]

y=ωst+φ1

ipa=Idca+I1acos(y+x1a)

ina=Idca-I1acos(y+x1a)

(1)

式中：M1、M2、M3分别为调制波基波、二倍频、三倍频分量调制比；φ1为调制波基波分量初相角；M22、M33为调制波二倍频、三倍频分量相对于2y、3y的初相；uspa和usna为A相上下桥臂调制波；ωs为调制波基波频率；Idca、I1a分别为桥臂电流直流分量、基波分量幅值；x1a为桥臂电流基波分量相对于y的初相。

当MMC工况已知，Idca、I1a、x1a随之确定，故在理论分析中将三者当作已知量。

2.1 子模块电容电压

首先对A相上桥臂子模块SM1进行分析。在MMC稳态运行时：

(2)

式中：ipasm1c为子模块SM1电容电流。

根据式(1)，A相上下桥臂开关函数可表示为[21]

M3cos(3y+M33)]

M2cos(2y+M22)-M3cos(3y+M33)]

(3)

式中：Saup、Salow分别表示上下桥臂开关函数。

子模块电容电流ipasm1c可表示为

ipasm1c=ipaSaup

inasm1c=inaSalow

(4)

为保持子模块电容电压的稳定，子模块电容电流直流分量应为0。

将式(1)、(2)、(3)代入式(4)，得

(5)

根据电容电压与电流之间的关系，子模块SM1电容电压Vpasm1c可表示为

(6)

式中：Vpasm1dc为上桥臂子模块SM1电容电压中的直流分量；c为子模块直流侧电容值。

类比分析，下桥臂子模块SM1电容电流inasm1c可表示为

(7)

实际运行中，同一相上下桥臂子模块电容电压直流分量相等，故下桥臂子模块SM1电容电压Vnasm1c可表示为

(8)

从式(5)和式(7)中可以得到如下结论：

(1)注入三次谐波使子模块电容电压中产生新的三次谐波分量，其幅值与桥臂电流直流分量、所注入的三次谐波有关。

(2)注入三次谐波使子模块电容电压中产生新的四次谐波分量，大小和幅值与注入的三次谐波和桥臂基波电流相关。

(3)同一相上下桥臂电容电压基波分量、三次谐波分量幅值相等，方向相反，二次谐波分量和四次谐波幅值和方向相同。

2.2 桥臂电压

根据MMC的运行原理，可得如下等式：

(9)

A相上下桥臂子模块输出电压upasm1、unasm1为

upasm1=Vpasm1cSaup

unasm1=Vnasm1cSalow

(10)

将式(3)、(5)、(6)代入式(10)，可得上桥臂子模块SM1输出电压各分量为

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

式中：upa1、upa2、upa3、upa4、upa5、upa6、upa7分别表示A相上桥臂子模块输出电压的基波、二次、三次、四次、五次、六次、七次谐波分量。upadc表示A相上桥臂子模块输出电压的直流分量。

上桥臂子模块SM1输出电压upasm1可表示为

upasm1=upa1+upa2+upa3+upa4+upa5+

upa6+upa7+upadc

(19)

类比分析，下桥臂子模块SM1输出电压unasm1可表示为

unasm1=-upa1+upa2-upa3+upa4-upa5+

upa6-upa7+upadc

(20)

upa、una可表示为

upa=Nupasm1

una=Nunasm1

(21)

因实际工程应用中一般要求子模块电容电压波动不超过额定电压的10%，由式(8)可知子模块电容电压波动幅度与子模块电容值成反比，又由文献[20]中未投入环流抑制时二倍频环流公式可知，子模块电容值越小，桥臂环流二倍频分量越小，桥臂电压二次谐波分量越小，环流抑制器输出的二倍频分量调制波幅值越小，因此实际工程应用中桥臂电压调制函数中二倍频分量调制比相对基波分量调制比而言一般较小，故可忽略式(16)中与调制函数二倍频分量有关的项，且不会对解析式精度造成太大影响，可得五次谐波分量近似解析式：

(22)

对MMC中A相和直流侧构成的回路列写KVL方程[20]：

(23)

提取直流分量等式：

(24)

解之得

(25)

式(25)中，由于二倍频调制函数幅值较小，因此式(25)中Ⅱ、Ⅲ部分相对Ⅰ部分较小，忽略Ⅱ，Ⅲ部分，得到子模块电容电压直流分量近似解析式：

(26)

由式(11)～(22)、(26)可得下列结论：

(1)注入三次谐波使得桥臂电压中产生新的五、六、七次谐波分量，上下桥臂六次谐波分量相同；五、七次谐波分量幅值相同，方向相反，会向交流系统输出五次谐波、七次谐波，危害电力系统的稳定运行。

(2)桥臂电压五次谐波分量主要受注入的三次谐波、基波调制比、桥臂基波电流影响；七次谐波分量受注入的三次谐波、桥臂基波电流影响。

(3)三次谐波的注入也会影响子模块电容电压的直流分量，但影响较小。其主要受基波调制比、桥臂基波电流影响。

3 三次谐波注入调制策略优化

根据式(16)、(17)、(19)、(20)可知上下桥臂电压五次、七次谐波分量方向相反，将会输出到交流侧，又考虑到奇次谐波会对电力系统产生巨大危害，例如增加线路的传输损耗、影响断路器和熔断器的正常动作。因此有必要对三次谐波注入调制策略进行优化。

可向调制波中注入微量的五倍频分量和七倍频分量，以达到减少输出五次、七次谐波分量的目的。

定义如下等式：

(27)

式中：uspaz、usnaz分别表示向A相上下桥臂新注入的调制波调制函数；M5、M7分别表示注入调制波的五倍频、七倍频分量的幅值；M55、M77表示五倍频分量、七倍频分量相对于5y、7y的初相。

先假设调制波五倍频、七倍频分量对子模块电容电压的影响较小，可忽略不计。

以A相上桥臂为例进行分析。作用在子模块上的五倍频和七倍频分量的开关函数，将会使子模块向外输出五次、七次和其他次谐波分量，若使增加的5次、7次调制波使桥臂子模块新向外输出的电压五次谐波分量、七次电谐波分量与桥臂电压原有的五次、七次谐波分量幅值相等、相位相差180°，即可达到减小桥臂电压五次、七次谐波分量的目的；在进行工程设计时，一般要求子模块电容电压波动不超过额定电压的10%，即电容电压基波、二倍频、三倍频、四倍频分量所占比重较小，所以可认为分别只输出五次谐波、七次谐波分量：

(28)

式中：upaz为新注入的五倍频、七倍频调制函数使A相上桥臂子模块输出电压增加的分量。

因为注入的三倍频分量一般调制比取1/6基波调制比，因此可认为式(16)中第Ⅳ部分占输出五次谐波分量的绝大部分。若使式(28)中五次谐波分量、七次谐波分量幅值与(16)中第Ⅳ部分、式(17)大小相等，方向相反，则可达到减小桥臂电压五次、七次谐波分量的目的。因子模块电容电压直流分量与额定电容电压相差较小，可近似认为两者相等，可得如下等式：

M55=M33+x1a+π

M77=2M33+x1a+π

(29)

实际工程应用中，根据MMC输出功率，即可求出MMC交流出口基波电压幅值和相角，随后可求出MMC输出基波电流相角和幅值，即I1a和x1a已知，M55、M77、M5、M7可全部求出，新增加七倍频、五倍频调制函数已知。

受IGBT过流能力的影响，I1a值不会过大；c值如果取得过小，会导致电容电压纹波幅值过大；N取的过大，则子模块数数目过多，系统复杂程度急剧上升；因此实际工程应用中M5、M7值较小。

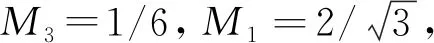
M7=0.000 345

M5=0.006 22

M7与M5计算所得值远小于M3、M1，可认为调制波五倍频、七倍频分量对系统的稳态运行无影响；七倍频、五倍频调制函数会通过电流影响电容电压的四、五、六、七、八次谐波分量，此时电容器阻抗较小且M5、M7较小，因此可忽略调制波七倍频、五倍频分量对电容电压的影响，即前述假设成立。

4 仿真验证及分析

为了验证解析式的正确性及优化策略的有效性，在PSCAD/EMTDC中搭建了5电平MMC模型。采用载波移相调制策略，交流系统采用单机无穷大系统，线电压有效值为5.5 kV，交流系统等效电阻为0.01 Ω，等效电感为72 mH；MMC中桥臂电感L为5 mH，直流侧电压为9 kV，载波频率为2 000 Hz，子模块电容值为2 800 μF。采用定有功功率和定无功功率控制方式，稳态运行时有功功率为0.8 p.u.，无功功率为0 p.u.；注入三次谐波幅值为基波幅值的1/6，初相与基波初相相同。以MMC中A相上桥臂为例，验证理论解析式的正确性。其中二倍频调制函数从仿真中获取。

4.1 解析式验证

图4为采用仿真、本文解析式计算子模块电容电压对比图。表1为仿真与解析计算A相上桥臂子模块电容电压各分量对比表。

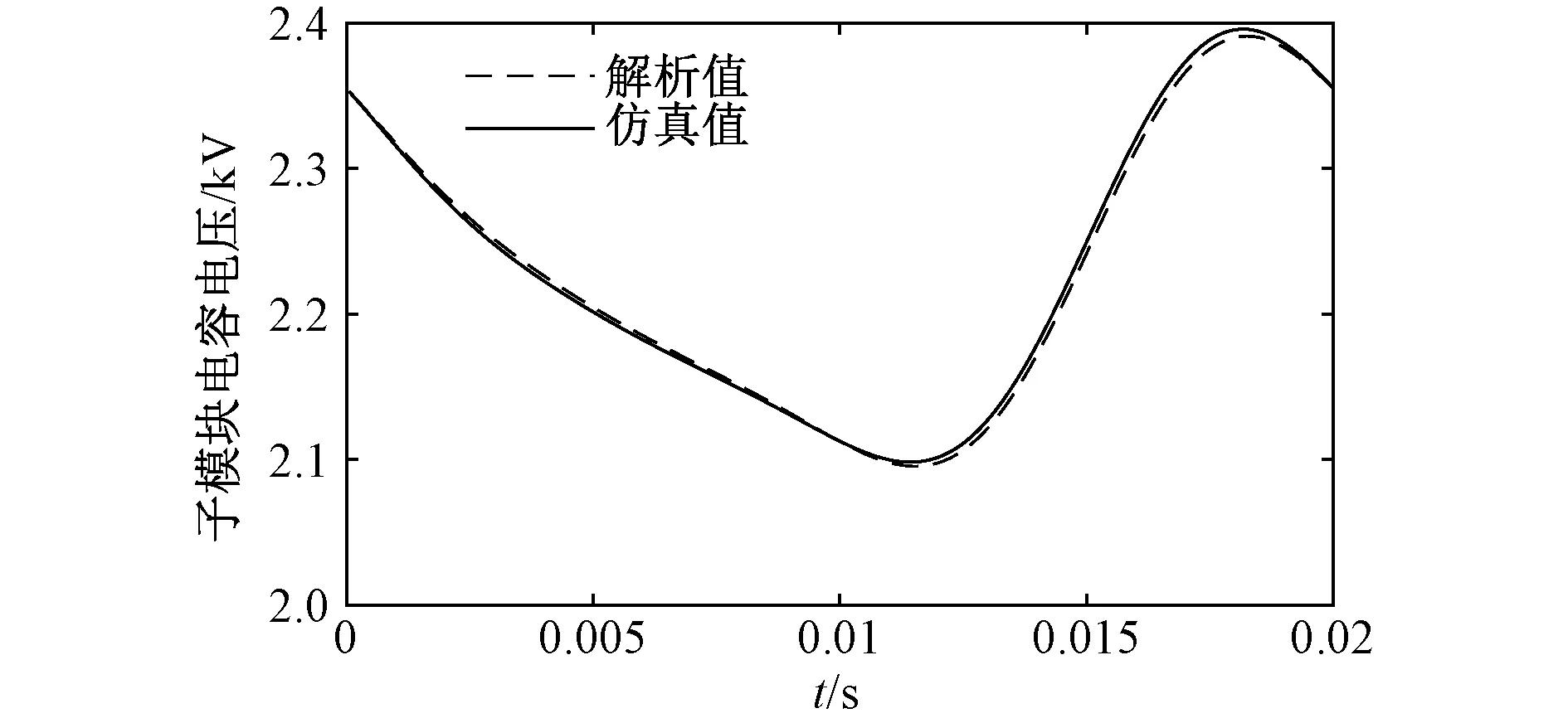
图4 子模块电容电压仿真和解析式计算对比Fig.4 Comparison of simulation and analytical calculation of capacitance voltage

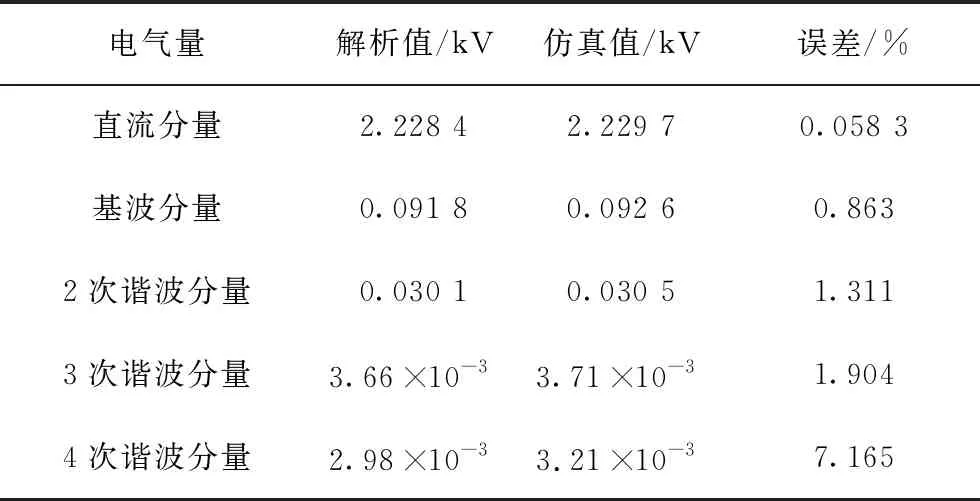
表1 仿真和解析计算式A相上桥臂子模块电容电压对比

从图4中可以看出，解析值与仿真值贴合较好，验证了本文推导解析式的正确性。虽然直流分量仿真值与额定电容电压仅相差0.020 3 kV，误差不大。但电容电压基波、二次、三次、四次谐波分量总有效值仅为0.096 4 kV，直流分量误差占电容电压基波分量、二次、三次、四次谐波分量总有效值的21%，会对电容纹波电压和功率半导体器件承受电压产生影响，且由式(25)可知，调制波基波频率和电容越小，直流分量偏差越大，因此有必要对直流电压进行修正。采用近似解析式(26)进行计算，所得直流分量值为2.225 1 kV，与采用式(25)计算所得值2.228 4 kV较为接近，误差为0.003 3 kV，占式(25)中Ⅰ、Ⅱ、Ⅲ部分解析值之和的15.27%，说明了采用近似公式也有较高的精确度。

图5、表2为采用仿真和本文解析式计算的桥臂电压对比图、各次分量对比表。

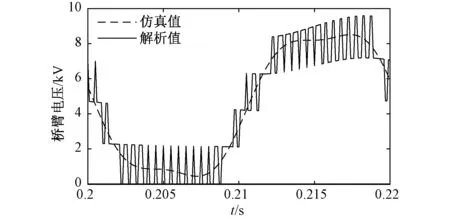
图5 仿真和解析式计算upa对比图Fig.5 Comparison of simulation and analytical calculation of upa

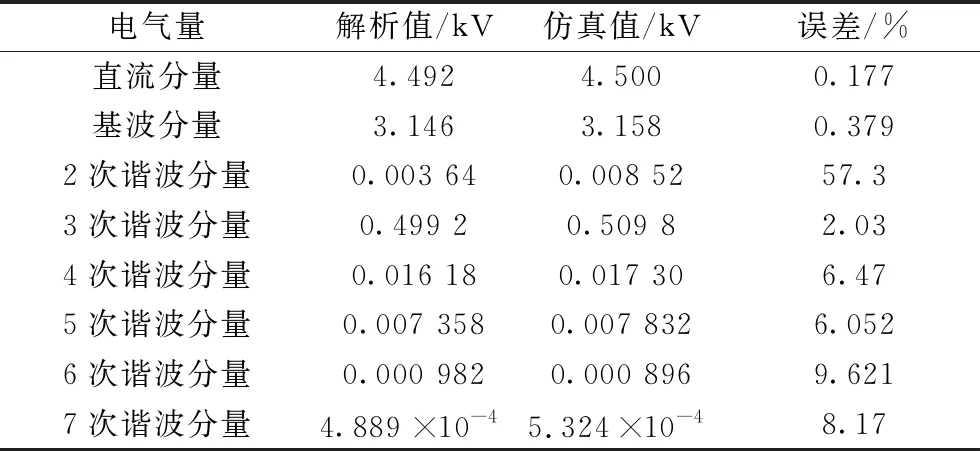
表2 仿真和解析式计算A相上桥臂电压对比

为了便于对比，PSCAD绘图步长选的较大。图5可以看出，解析式所得结果与仿真波形趋于一致，吻合较好。实际上，MMC的载波移相调制策略是由多个正弦脉宽调制组成的，本文利用开关函数分析各主要电气量的频谱，而正弦脉宽调制的理论基础为面积等效原理，故图5中仿真数据图形与解析数据图形相比有一定误差；但从表2可以看出，直流分量、基波分量、三次谐波分量误差较小；其中六次谐波分量、四次谐波分量误差所占百分比较大，但仿真值与解析值差值较小；二次谐波分量误差占仿真值的57.3%，但误差值为0.00 488 kV，相对基波分量而言较小，因此误差是可以接受的；五次谐波分量误差为6.052%，七次谐波分量误差为8.17%，是由于环流抑制器不能将环流完全抑制，桥臂电流中还含有一定量的各次环流。若采用五次谐波分量的近似解析式(22)进行计算，计算所得值为0.007 197，与仿真数据相比误差为8.107%，相比精确解析式(16)，误差增加了2.055%，验证了五次谐波分量近似解析式的正确性。

由表1、2中数据可知，误差最大分量分别为子模块电容电压四次谐波分量和桥臂电压二次谐波分量，误差值分别为2.3×10-4kV、0.004 88 kV，分别占仿真值的7.165%、57.3%，但相对于直流分量2.229 7 kV、基波分量3.158 kV而言，其误差值极小；又由于实际工程中的各种非理想因素也会造成一定的误差，因此解析式是能够满足工程设计需要的。

从表2可知，因MMC输出三次谐波电压可通过合理选择变压器予以滤除，因此MMC输出电压中主要包含五次、七次谐波分量，考虑到奇次谐波会对电力系统造成巨大危害，例如降低输电线路传输效率、引起电网中局部的并联和串联谐振、影响断路器和熔断器的正常动作，因此有必要改进三次谐波注入调制策略。

4.2 调制策略优化验证

图6为优化前后桥臂电压对比图，表3为优化前后桥臂电压各分量对比表。

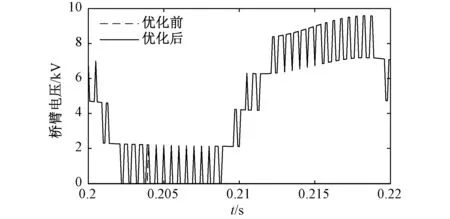
图6 优化前后对比图upa对比图Fig.6 Comparison chart before and after optimization of upa

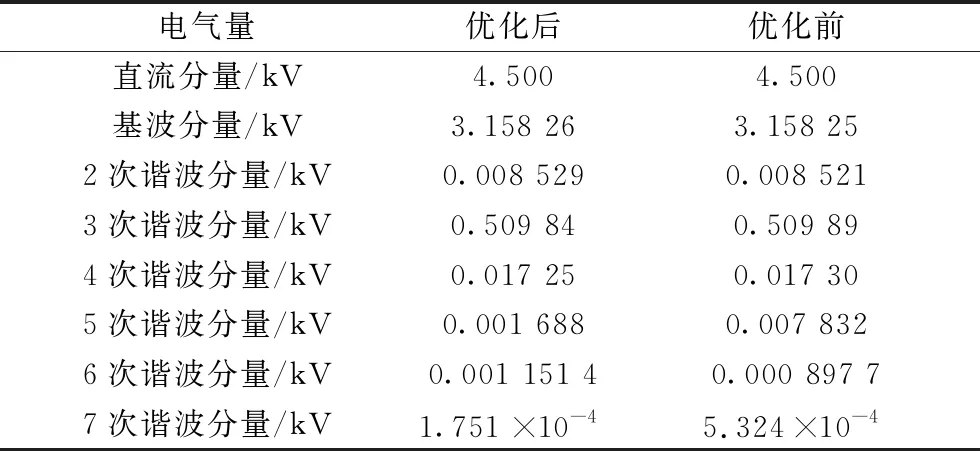
表3 优化和未优化A相上桥臂电压对比

从图6、表3中可以看出，采用改进与未改进调制策略的桥臂电压除五次、七次谐波分量外，其它分量与优化前相差不大，而优化后的五次、七次谐波分量则降低为0.001 688 kV、1.751 ×10-4kV，为未优化时的21.5%、32.8%，验证了本文所述改进三次谐波注入调制策略的有效性。

5 结 论

为了深入了解采用三次谐波注入调制策略的MMC内部运行机理，本文利用开关函数分析了MMC的稳态运行特性，并给出了子模块电容电压、桥臂电压的理论解析式。得出了以下结论：

(1)三次谐波注入策略会在子模块电容电压中引入新的三次谐波分量和四次谐波分量；上下桥臂子模块电容电压二次、四次谐波分量大小和方向均相同，基波、三次谐波分量大小相同，方向相反。

(2)三次谐波注入策略会在桥臂电压中引入新的五、六、七、次谐波分量，其中上下桥臂五、七次谐波分量大小相同，方向相反，将会输出到交流侧；六次谐波分量大小和方向均相同。

(3)采用三次谐波注入调制策略在桥臂电压产生的七次谐波分量，其大小与注入的三次谐波幅值及系统工况有关。产生的五次谐波分量也主要受注入的三次谐波影响。

本文根据桥臂电压理五次、七次谐波分量理论解析式，对三次谐波注入策略进行了改进，很好地减少了采用三次谐波注入调制策略时，桥臂电压上产生的五次、七次谐波分量。本文所得解析式和优化策略具有一定的工程实践价值，能够为相关工程应用提供理论基础。