基于加权灰度熵差的分区域曝光算法

胡晓彤 刘 楠 朱博文

(天津科技大学计算机科学与信息工程学院 天津 300457)

0 引 言

曝光算法是一种依据曝光控制参数对曝光时间进行调整的算法，利用曝光算法可使不同场景下的图像得到合适的曝光，有利于后续图像分析。曝光算法在高清摄像机[1-3]、实时视频记录[4]、智能手机[5]、火焰图形分析[6]、航空航天[7]、无人驾驶[8]、医学[9]、图像融合[10-14]等领域已得到了广泛的使用。

目前，相关学者已对曝光算法展开了深入的研究。Goossen等[15]提出的灰度平均值法是根据图像灰度平均值的大小调节曝光时间使图像亮度适中的曝光算法。Rahman等[16]提出的信息熵法是根据图像的信息熵计算曝光时间。甘玉泉等[17]提出的图像分区法在不同类型场景下使用特定的调光来达到最佳曝光效果。戈志伟[18]提出的基于数值分析的调光方法是通过实验得到一组曝光参数与图像亮度的关系，运用数值分析寻找方程根，从而计算出最佳的曝光参数值。Shimizu等[19]提出的曝光算法引用HIST参数，使用模糊逻辑来计算曝光量。Su等[20]将亮度特性作为控制参数，将其建模为凹函数或凸函数，使用改进割线算法计算最优曝光参数。解静等[7]提出的以能量分析为基础，对目标进行加权统计，并采用最速查表法获得最佳曝光时间的算法已成功应用在空间照相机上。马泽龙等[21]提出了一种基于图像直方图特征函数的自动曝光方法，可在背景亮度变化快、变化范围大的情况下实现高速相机的自动曝光控制。

上述曝光算法在消费级相机中已有较好的应用，但在监控场景下(如强烈侧光或背光的环境)仍存在不能适应背光或正面强光等复杂光照环境的缺陷。灰度平均值法[15]认为图像的平均灰度值为灰度级中位数时曝光效果最佳，但这会把原本过亮或过暗场景的亮度调整至灰度级中位数时的亮度，使图像失去原有特点。信息熵法[16]使用图像信息熵的最大值作为最终收敛结果，在一定程度上弥补了灰度平均值法的缺点，但其在强光条件下仍得不到合适的曝光。图像分区法[17]按一定策略将图像分为多个区域，使其对不同场景的处理更具有针对性，但当对比度反差较大时也使用同一曝光参数，会使局部图像无法得到符合其特征的曝光。

为解决上述问题，本文提出基于加权灰度熵差的分区域曝光算法(WDGE)。首先，估算曝光时间得到基准图像；再依据加权灰度熵差对该图像进行区域分割并计算出各子区域的最佳曝光时间；最后将各子区域拼接，实现分区域成像。

1 传统曝光算法

传统的曝光算法一般选取图像的灰度平均值或信息熵作为曝光控制参数。

灰度平均值法是根据图像灰度平均值的大小调节曝光时间使图像亮度适中的曝光算法。灰度平均值计算公式如下:

(1)

式中：Gmean为图像灰度平均值；G(i,j)为图像第i行第j列像素的灰度值；l与c分别代表图像像素阵列的总行数与总列数。灰度平均值法一般将灰度级的中位数所对应的曝光时间作为最终结果，即图像的灰度平均值越接近中位数，图像细节描述得越清晰，曝光效果越好。灰度平均值与曝光时间映射关系如图1所示。

图1 灰度平均值与曝光时间映射关系

可以看出，灰度平均值随曝光时间增大呈单调递增趋势。但在亮度较低或亮度较高的场景下，最终曝光结果都定位至灰度级的中位数所对应的曝光时间则不能得到实际场景的曝光效果。

另一方面，熵作为图像所具有的信息量的量度[22],信息熵越大，图像质量越好[23]。因此，信息熵法则利用图像的信息熵(Entropy)作为反馈量来调节曝光时间，完成曝光评价。信息熵的计算公式如下：

(2)

式中：k表示图像的灰度级数；Pi为各灰度级出现的概率。由式(2)可知，当所有的灰度分布均匀时，信息熵最大。此时，各个灰度级出现概率相同，即：

(3)

此时对应的最大信息熵为：

(4)

信息熵与曝光时间映射关系如图2所示。

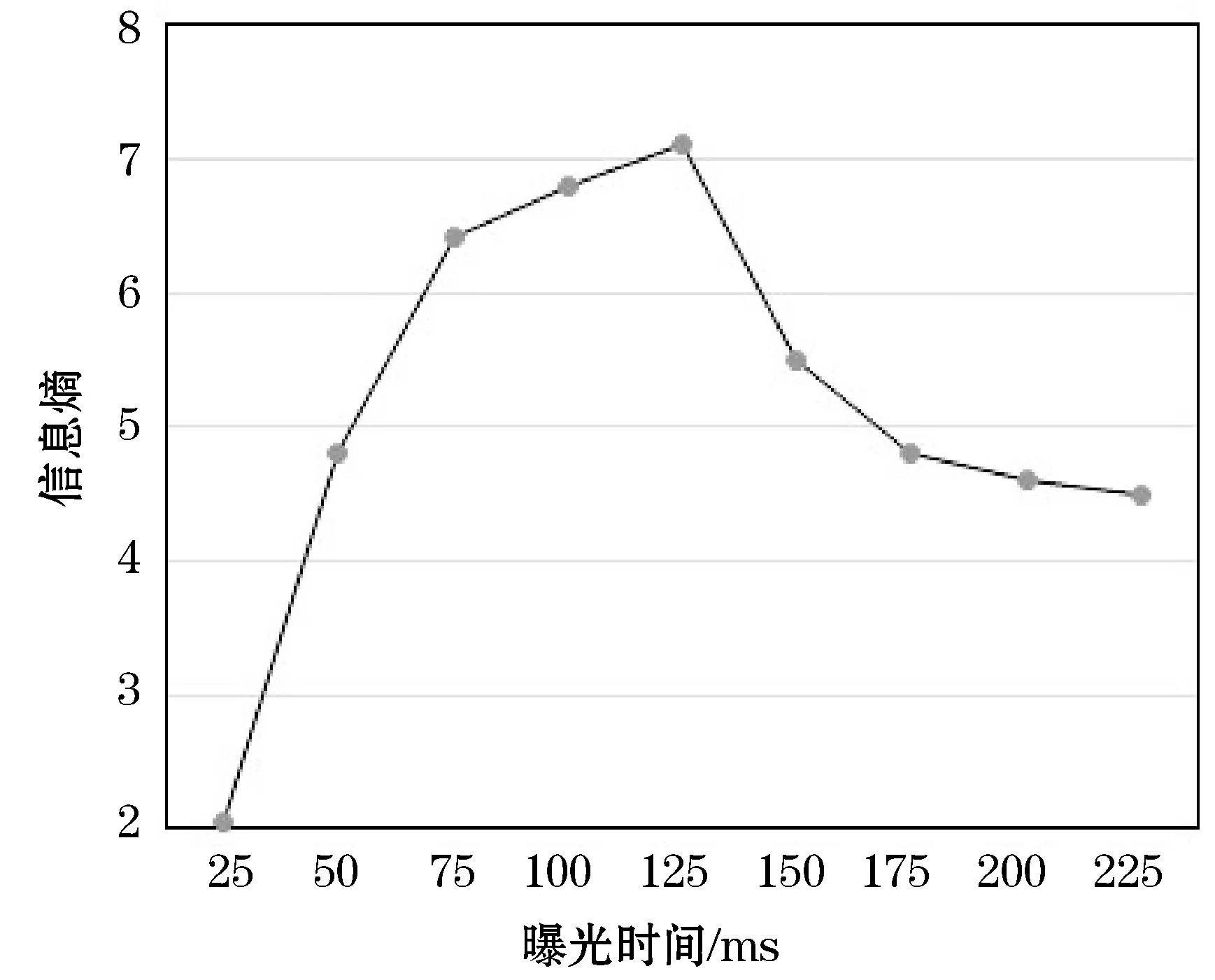
图2 信息熵与曝光时间映射关系

2 加权灰度熵差

灰度平均值描述的是整幅图像的灰度平均值，当灰度平均值越接近中位数时，曝光效果越好；信息熵描述的是整幅图像中各灰度值分布的概率，信息熵越大，曝光效果越好。因此，本文将灰度平均值与信息熵结合，提出一种新的曝光控制参数，该参数融合了灰度平均值与信息熵两者的优势。

信息熵越大，曝光效果越好，故将信息熵单独作为一项，即：

(5)

式中：UE为归一化的信息熵；E为图像信息熵；d为图像深度。

灰度平均值越接近中位数时，曝光效果越好，故将灰度平均值与灰度级中位数的差值作为一项，即：

(6)

式中：UG为归一化的灰度平均值与灰度级中位数差值；Gmean为灰度平均值；Gmedian为灰度级中位数；d为图像深度。

融合UE和UG选取两种方式进行讨论，分别是求和与作差，即：

US=α×UE+(1-α)×UG

(7)

UD=α×UE-(1-α)×UG

(8)

式中：US和UD分别为UE和UG求和与作差的结果；加入权重值α，对在不同场景下的UE和UG合理分配比重，从而得到最佳效果。

US和UD与曝光时间的映射关系分别如图3和图4所示。

图3 US 与曝光时间映射关系

图4 UD与曝光时间映射关系

由图1和图2可知，信息熵、灰度平均值与灰度级中位数的差值两个参数与曝光时间的映射关系分别收敛于(0，Emax)、(0，Gmedian)，则两项相减结果必定收敛。由图3和图4可知，UD相较于US，UD只存在一个极大值，可将极大值作为最终曝光结果。

综上，选取UD作为新的曝光控制参数——加权灰度熵差，既满足了信息熵越大、灰度平均值越接近中位数，曝光效果越好的规律，又保证了算法的自适应性。最终，加权灰度熵差的计算公式为：

|Gmean-Gmedian|

(9)

求得加权灰度熵差与曝光时间映射关系后使用二分法递归求得最佳曝光时间Xn+1，公式如下：

(10)

X0、X1为给定的两个初始曝光时间点。

与单独使用灰度平均值或信息熵作为曝光控制参数的传统方法相比，本文提出的加权灰度熵差融合了灰度平均值与信息熵，选取极大值作为最终结果在保证了算法自适应性的同时，将图像灰度均值与各灰度值出现的概率分布融合在一起，增强了对图像的描述能力。

3 分区域曝光算法设计

在景物对比度差异较大的复杂场景下，使用统一的曝光时间，部分景物会出现过度曝光或欠缺曝光的情况。文献[17]使用的分区曝光算法是将整幅图像人为分成不同的区域，并对各个区域赋予不同权值，最终求得一个加权后统一的曝光结果。这种方法无法将图像中所有细节都调整至相对于其子区域来说最佳的曝光效果。而本文提出的区域分割策略是将场景分为不同感光特性的多个子区域，然后计算每个区域的最佳曝光时间，从而使整幅图像得到适宜的曝光，避免出现过度曝光或欠缺曝光的情况。

本文提出的基于加权灰度熵差的分区域曝光算法的基本思想如下：先对图像进行曝光时间估算，将其调整至一个相对合适的曝光时间。在此基础上根据图像的加权灰度熵差和预设阈值确定过曝光区域和欠曝光区域。然后，计算不同区域的加权灰度熵差值，再根据其与曝光时间的映射关系使用二分法求得曝光时间,最后将经过曝光调整的过曝光区域和欠曝光区域与正常曝光的子区域拼接，从而得到最终的曝光图像。

在成像过程中，曝光时间的初始值设置非常重要。在一些高反差的复杂场景下，初值的确定会影响最终成像效果。所以本文在区域分割前对图像进行曝光时间估算，即计算得到基准曝光时间，把该曝光时间下的图像作为基准图像。

首先要确立基准图像的加权灰度熵差，公式如下：

U=tm×um+tl×ul+th×uh

(11)

tm+tl+th=1

(12)

式中：U为基准图像的加权灰度熵差；um为原始图像的加权灰度熵差；ul为低于um的区域的加权灰度熵差；uh为高于um的区域的加权灰度熵差；tm、tl、th为归一化因子。为了使U在场景过亮和过暗时受到较小的影响，设置tm>tl且tm>th。再根据图3，选取加权灰度熵差U所对应的曝光时间作为基准曝光时间，得到基准图像。

本文使用的基于加权灰度熵差的区域分割法具体方法如下：

(13)

式中：U*为当前图像区域的加权灰度熵差；Th为过曝光阈值；Tl为欠曝光阈值；Eh为过曝光区域；El为欠曝光区域；A为正常曝光区域。当U*大于Th时，该像素属于Eh；当U*小于Tl时，该像素属于El；当U*大于Tl且小于Th时，该像素属于A。

区域分割后，根据式(9)计算各个区域的加权灰度差，再根据式(10)及图4计算求得曝光时间。最后将经过曝光调整的各个区域拼接在一起得到曝光结果，拼接过程如图5所示。

图5 各区域图像及拼接结果

特别地，为了排除噪声等干扰因素，当过曝光区域与欠曝光区域小于整幅图像面积占比的20%时，不执行区域分割策略。

4 实验结果与分析

本文选取三类不同的场景进行实验。场景A是在较亮的室内场景；场景B是有过曝光区域的室内场景；场景C为有人的背光场景。实验电脑配置为CPU Intel(R)Core(TM)i5-3210 M 2.50 GHz，内存4 GB。

4.1 图像评价指标

实验选取EAV、灰度方差和Tenengrad梯度作为评价指标，评判曝光算法的成像效果。

EAV是王鸿南等[24]提出的图像评价指标，其计算公式为：

(14)

式中：m和n为图像的长和宽；df为图像在坐标为(x,y)点的8邻域各方向上的灰度变化幅度；dx为像素间的距离增量。即该方法是对图像每点周围的灰度扩散程度的统计。

灰度方差的计算公式为：

(15)

Tenengrad梯度是采用Sobel算子分别提取水平和垂直方向的梯度值，其计算公式为：

(16)

(17)

(18)

式中：Ten为Tenengrad梯度值；m和n为图像的长和宽；S(x,y)为该点处的梯度；g(x,y)为坐标为(x,y)点的灰度值；Gx和Gy为两卷积核。

4.2 α值的选取范围

将式(9)中α值设置为0.3、0.4、0.5、0.6和0.7，分别计算三类不同场景下的图像评价指标，取其平均值作比较，结果如图6-图8所示。

图6 不同α计算得到的图像EAV值

图7 不同α计算得到的图像灰度方差

图8 不同α计算得到的图像Tenengrad梯度

由图6-图8可知，当α取0.5～0.6时，图像评价指标最高，则认为在此区间内的α值可满足大多数场景下的彩图。

4.3 算法对比及分析

本文使用对比算法和基于加权灰度熵差的分区域曝光算法在三类场景下进行实验。对比算法分别是:灰度平均值法[15](Grey-scale average Method, GAM)、信息熵法[16](Entropy Method, EM)、图像分区法[17](Scene Analysis Method, SAM)和改进割线法[20](Model-based Approach, MA)。

场景A是较亮的室内环境，该场景下的效果比较如图9所示。使用灰度平均值和信息熵作为曝光控制参数的曝光算法，在一定程度上均提升了曝光效果。而使用本文提出的算法在场景评估时，判定不需要区域分割，所以直接计算加权灰度熵差并选取最佳曝光时间。

图9 场景A的各算法效果比较

表1为场景A下不同曝光算法后得到曝光结果的图像评价指标。此时，本文算法不执行区域分割策略，计算整幅图像的加权灰度熵差作为曝光控制参数。可以看出，相较于使用灰度平均值或信息熵作为曝光控制参数，加权灰度熵差作为曝光控制参数的三类图像评价指标均为最高，提升范围由2.18%到27.74%。

表1 场景A下各算法所得结果的评价指标

场景B下的效果比较如图10所示，图10(a)中窗外区域过度曝光导致窗外图像模糊不清，且室内区域亮度较暗，丢失了大部分图像细节。图10(b)与图10(a)相比，窗外区域得到合适曝光，但室内区域的曝光效果欠佳。图10(c)、图10(d)中窗外区域得到了合适的曝光，但室内区域处于欠曝光状态，丢失了大部分图像细节。在图10(e)中窗外区域得到合适曝光的同时，室内区域的图像信息也得到了很好地展现。因此在场景B中使用本文算法可使室内、窗外区域均得到合适的曝光，显著提升了图像视觉质量。

图10 场景B的各算法效果比较

场景C背光区域亮度过高，其效果比较如图11所示。图11(a)与(c)均无法将背光区域调整至合适曝光的状态以展现该区域的图像细节。图11(b)、(d)与(a)、(c)相比，背光区域的曝光效果得到改善，图像细节得到了很好的展现，但其余区域曝光效果更差。图11(e)将背光区域调整至合适曝光的同时，室内区域及人物部分的效果也有提升。所以在场景C下使用本文提出的算法可使背光区域、室内区域和人物区域均得到合适的曝光。

图11 场景C的各算法效果比较

表2-表3分别为场景B、C下使用不同曝光算法后得到曝光结果的图像评价指标。在场景B、C下，使用本文提出的加权灰度熵差作为曝光控制参数，同时使用分区策略，三类图像评价指标同样均为最高，虽然文献[17]也使用了一定的分区策略，但最终结果没有本文算法好。文献[20]求得最佳曝光结果的图像评价指标也低于本文算法的曝光结果，本文算法相较三个对比算法提升了29.09%到131.86%，充分验证了使用该算法可得到较好的曝光效果。

表2 场景B下各算法所得结果的评价指标

表3 场景C下各算法所得结果的评价指标

5 结 语

针对传统曝光算法无法较好地适应复杂场景这一问题，本文提出了一种基于加权灰度熵差的分区域曝光算法。首先提出了一种新的曝光评价指标——加权灰度熵差，由于其结合了灰度值与信息熵的优势，所以使其具有更强的场景描述能力；随后，利用分区域曝光算法，通过曝光估算、分区曝光和图像拼接等步骤，实现根据场景特征的分区域曝光。实验表明，使用本文提出的加权灰度熵差能准确地找到与场景特征相匹配的最佳曝光时间，并增强整体场景及局部细节，提高了图像品质。