新医科专业傅里叶变换虚拟仿真实验平台的构建与实现
孔祥慧,方 晖,夏 天,徐罗元,刘淑贤,刘东艳
(1.河北医科大学医学影像学院,河北石家庄 050013;2.上海培云教育科技有限公司,上海 200433)
0 引言
随着科学技术的快速发展,虚拟仿真实验越来越受到重视,各高校根据学校自身和学生特点,分学科、分专业地将虚拟仿真和大学传统课堂有机结合,更好地培养学生的动手能力、创新精神和科学素养,从而提高教学质量和学生的综合素质。目前,各高校在大学物理[1]、电子电工[2]、生物化学[3]、分子生物[4]、病理学[5]、生理学[6]、药学[7]、基础医学[8]等多个学科和专业积极开展虚拟仿真实验的构建,并着手应用到教学和实验中,取得了良好的教学效果,学生也受益颇多。
我国医学影像技术专业是依据医疗各学科的需要而发展起来的专业性极强的理工科专业[9-10],是医学与理工融合的新医科专业,对数学知识的要求也就越来越高。很多医学院校都在高等数学课程的基础上开设了工程数学课程,而傅里叶变换是工程数学的核心内容之一,也是医学影像技术专业后期《医学影像成像原理》《图像处理》等课程的理论基础。但目前傅里叶变换理论知识与医学实际应用的结合还有所欠缺,为更好地将傅里叶变换与影像专业技术相结合,应积极改变教学方式。尝试建立傅里叶变换虚拟仿真实验平台,以适应时代和科技的发展,培养新型医学影像人才。
1 医学影像技术专业工程数学傅里叶变换教学现状
1.1 理论知识抽象,难以理解
傅里叶变换相关知识比较抽象,学生难以理解,造成一定的教学困难。傅立叶级数是傅立叶变换的基础,傅立叶变换是由傅立叶级数推演而来,傅立叶变换的公式的表达形式多样,包括积分形式和三角形式,涉及相关知识范围广、抽象,对于初学者来说,理解起来较为困难。
1.2 教学方式单一,缺乏实践
数学课程本身较其他学科显得枯燥,工程数学更是如此,虽然目前很多数学教师在积极探索新的教学方式和方法,但是有时可能因为特殊情况(如班级容量较大等)而未能完全实施[11]。再加之国内高校很少开设工程数学实验课程,单纯理论教学方式太过传统和单一,学生没有动手操作的实践机会,很难达到良好的教学效果,对于大多深奥的知识只是浅尝辄止,并不能深究。
1.3 教学模式不合理,与应用衔接困难
医学影像相关专业开设的工程数学课程,傅里叶变换教学内容并没有充分的和医学相关知识相结合,体现学科的特殊性。学生完成教学课程后,依旧对其图像处理和分析应用没有更深的理解。此教学模式造成知识断层,理工科和其相关医学应用的衔接困难。
1.4 学生仅了解应用,忽略原理探索
目前,医学影像技术专业走到了一个瓶颈期。学生观念还是停留在对于医学影像设备的临床应用,而缺乏成像原理与图像处理的探究。例如在图像处理方向上,如何将图像优化、去除噪声、提高清晰度等,仅限制在应用上。由此可见,薄弱的数学基础限制了本专业的学科发展和人才技术水平的提高。
1.5 学生深造及创新空间受限
医学影像技术专业毕业的学生获得的是理工学士学位,学生毕业深造可以沿生物医学工程或图像处理方向发展,但由于数学功底较差,会造成基础不扎实,难以选择更多的深造方向,创新空间也会受到极大的限制。
2 傅里叶变换虚拟平台建设的必要性
2.1 多学科交叉,覆盖面广
医学影像技术专业是一个医理工结合的交叉学科,其涉及多专业的相关知识。虚拟仿真实验教学统一布局、多学科交叉、分层次、有重点,可以满足对学生基础理论的认知、专业技术的掌握和实际设计与综合应用能力培养的要求[12]。通过此虚拟平台,加快学生形成“医工融合”的观念,对自己的专业有更深的理解,将理工科知识应用到医学中去。
2.2 具有创新性,可针对医学生开展实验课程
傅里叶变换知识抽象、晦涩,因此实验是该门课程不可缺少的一环,通过实验可使抽象的概念形象化,枯燥的内容趣味化,能够收到良好的教学效果,有利于培养学生的学习兴趣,提高其创新意识和实践动手能力[13]。此平台的建立,主要针对医学院校开展相关数学实验,循序渐进,引导学生将理论应用于医用相关实践中。此外,该虚拟平台与示波器进行相关波形实验相比,可不受无干信号的干扰,可观察到更理想的波形变化。
2.3 培养新型高端影像技术人才
医学影像技术是进行医学检查的一项常用技术,该项技术的应用面非常广泛。伴随着医学影像技术的广泛应用,人才市场对医学影像技术人才的需求也随之增加。不少高校依据人才市场对该项技术人才的广泛需求,有针对性地设计了相关人才培训计划,并在高校设置以培养医学影像技术人才为目标的医学影像技术学的专业课堂,对教材内容、课堂设计等方面也适时进行了技术创新和改革[14]。积极开展相关教学改革,该虚拟平台的构建,可初步培养学生建立起数学与影像技术关系的思维,而不是将两者剥离。学生可以在该平台发挥他们的创造力,推动学生内部学术交流,激发更多地灵感,实现共同进步。
3 傅里叶变换虚拟仿真实验平台的设计和实现
傅里叶变换虚拟仿真实验平台分为4 个模块,如图1 所示,分别为基础知识、典型案例、心电图和二维傅里叶变换等子模块。4 个模块由浅入深地将抽象的傅里叶变换理论知识具体化、形象化,并充分与其应用联系起来。

图1 傅里叶变换虚拟仿真实验平台构成
3.1 基础知识模块
作为工程数学重要的一部分,傅里叶变换发挥着重要的作用。傅里叶指出,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示:

的级数称为傅里叶级数。

式中:a0、an、bn为傅里叶系数。而傅立叶变换是能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合,可对不同的波进行分解。
但此公式较为抽象,学生无法了解各个参数的意义,也就难以理解傅里叶级数时域和频域转化的真正意义。该模块着重实现学生对傅里叶级数的初步认识,理解各种波时域和频域的转换,通过时域的波形和频谱图进行对比深入理解傅里叶变换。在该模块中,通过调整不同正弦波信号,每个输入项含频率、幅值、初相位3 个输入参数,将各个正弦波叠加,可得到不同波形的信号波形及频谱图。学生通过此模块可更加深刻地理解傅里叶级数的原理及改变各个参数对波形图的影响。
例如通过调整合适的频率、幅值、初相位输入参数可以得到矩形波图像,如图2 所示。

图2 矩形波及其频谱图
3.2 工作原理
通过第一模块的学习,学生已能初步理解傅里叶变换。但对于影像专业的学生,需要将理论应用于实际。虚拟平台第2 模块介绍傅里叶变换简单的实际应用,构建了两个典型案例模块,分别为音频采集模块和磁共振射频模块。
3.2.1 音频采集
为更加形象地展现傅里叶变换在实际中的广泛应用,该模块对声音进行傅里叶变换,让无形的声波可视化。根据所学知识,声波也是一种波,可通过正弦波的叠加得到,即也可表示为傅里叶级数。在该模块,学生自己录制声音,软件生成音频时域信号。点击“FFT Audio”后,软件可将时域信号通过傅里叶变换生成频域信号。由频谱图可以看出人声是由低频信号组成,点击“filter”中的低通滤波对频率波形进行处理,显示波形和原波形可进行对比,如图3 所示。
通过此模块帮助学生理解生活中常见时域信号与频域信号的关系,以及滤波器的功能作用。
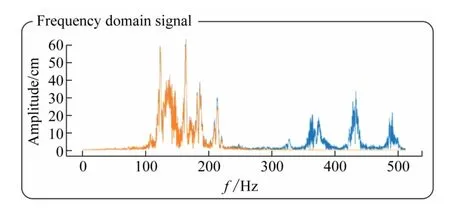
图3 音频滤波前后对比图(蓝色为滤波前信号,橙色为滤波后信号)
3.2.2 核磁共振
该模块是傅里叶变换的医学应用,为更贴近医学影像技术专业学生的使用和理解,能更好促进“医工结合”。在医学成像理论中,学生们已经了解了核磁共振成像原理。利用核磁共振成像,把人体放到梯度场强中,施加一个与人体氢质子旋进频率相同的射频脉冲进行激发,使人体内的氢质子产生核磁共振现象,核磁共振会释放出微弱电磁波,通过线圈接收这个信号,再经过傅里叶变换和k空间的填充(k空间为一个抽象的频率空间,一个以空间频率为单位的空间坐标系所对应的频率空间),最终可得到核磁共振的图像。磁共振成像中,对于不同层厚的选择,需要进行选择性激励,即用一个有限频带(窄带)的射频脉冲仅对共振频率在该频带范围的质子进行共振激发。在该模块中代表有限频带的射频脉冲有方波与sinc 波信号,分别对应磁共振信号中的硬脉冲(hardpulse)与软脉冲(softpulse)信号,探究这两个信号的特点及频域与时域的变化关系。以方波脉冲为例,其函数及其傅里叶变换,F(ω)=,频带脉宽,可知脉宽和频带成反比。该模块中T 为方波信号的周期,t为时域信号持续时间(可选择500,800,1 000,2 000 μs 4 个档位),N 为Sinc 波瓣个数。例如将周T 从1 000 μs改为100 μs,如图4 所示。通过T =100 μs宽度频域信号(橙色)与T =1 000 μs 宽度(蓝色)频域信号进行对比可知,当方波信号宽度增加时,相应的频率带宽会变窄,幅值变高。
同样对于sinc波的周期T 进行变化时,学生们也可以得出当周期T 变化时,频率和幅值的变化,并得出相应的结论。由此将两种波形傅立叶变换后的波形进行比较,学生可自我总结出何种波形更适合与磁共振成像中的选择性激励。
3.3 心电图应用
心电图是由一系列波组所构成的,因此心电图也可以通过傅里叶级数进行分析。在该模块,可绘制心电图的频谱图,发现在频率为0 的地方有一个很强的直流信号,该信号的存在极大地压缩了其他频率的幅度,通过基线矫正(baseline correction)可以将此直流信号滤掉。此外,该模块有低通、带阻、带通滤波器可供选择,学生可自行选择各种类型的滤波器,比较各种滤波下频率图的差别。例如选择带阻滤波器时可以观察到50~100 Hz频率被压制,将此频域信号转化为时域信号并局部放大后可见曲线变得更加光滑,如图5所示。

图4 不同宽度的方波信号频域对比图

图5 带阻滤波器滤波前后对比图
3.4 二维傅里叶变换模块
在医学实际工作中,医学影像图像是二维的灰度图像。根据诊断和治疗的需要,有时需对影像进行处理。医学影像图像通常在计算机内部以二维离散数据矩阵的形式进行处理,因此有必要进一步研究二维离散傅里叶变换及其逆变换。
二维的灰度图像数据常表示为

为方便处理,一般选择方形数据,M =N。离散傅里叶变换定义和推导如下:


上述公式常用于将图像的灰度分布函数变换为图像的频率分布函数,逆变换则是将图像的频率分布函数变换为灰度分布函数。
在该模块中,学生可选择灰度图像样品,进行二维傅里叶变换。如选择图像处理经典图片Lena图,进行二维傅里叶变换后可得到频谱图和相位谱图,由于谱图中频谱的动态范围很大,图像显示很不明显,可进行一次对数变换,得到傅里叶变换后实部、虚部、频谱以及相位谱图像,如图6 所示。
由于频谱图移频到原点后,图像的频率是以原点为中心对称分布的,所以可以清晰看出图像的频率分布,如图7 所示。此外,移频后可以分离有周期性的干扰信号。若移频后的频谱图除原点以外还存在以某一点为中心、对称分布的亮点,则这些亮点是由干扰信号产生的。
通过此模块可以对二维傅里叶变换有更深刻的理解和认识,对后期的图像处理课程以及医学影像图像的处理都有很大的帮助。

图6 Lena图的谱图

图7 移频后的谱图
4 实证分析
4.1 对象和指标
为检验此虚拟平台的教学效果,对130 名医学影像技术专业学生开设工程数学实验课课程。在完成相关理论课程后,学生在老师的指导下上机进行操作。通过一学期的课程教学,将学生自我评价进行反馈和统计。
4.2 统计分析
由图8 所示统计数据可以看出,学生在自我评价中都有较好的反应。其中在理论联系实际能力、创新意识、对知识的理解和自主学习方面有较明显的提高。尤其在理论结合实际方面,学生有较大的提高,为后期CT、MRI成像原理课程的学习奠定了良好的基础。
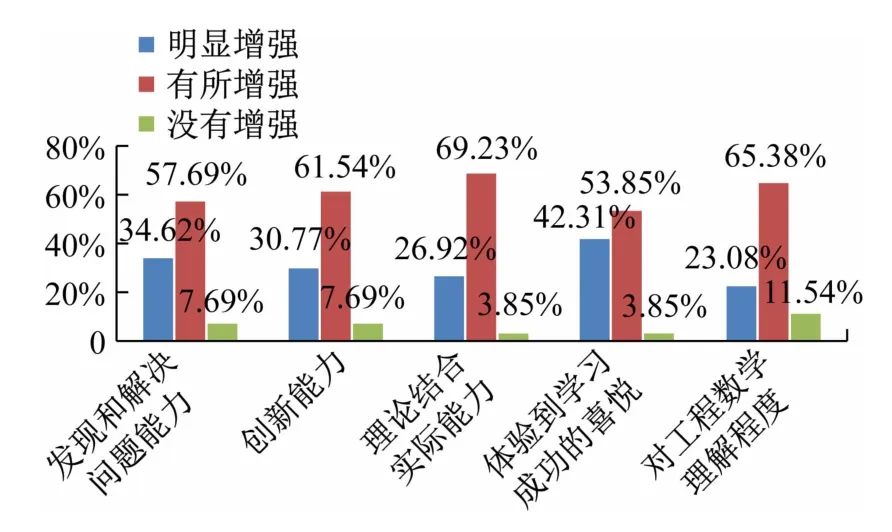
图8 学生自我评价
5 工程数学其他模块构建虚拟仿真实验平台的可行性及展望
工程数学所涉及的知识非常广泛,主要包括《线性代数》《概率统计》《计算方法》《积分变换》《复变函数》这几门课程。如果也能将数学实验和这些课程的教学结合到一起,可能会收到很好的效果[15]。不仅傅里叶变换对于医学影像技术专业学生有重要意义,卷积和线性代数等相关知识,也都与医学图像后处理有着密不可分的联系。为实现理论和实验相结合,将工程数学更充分地应用于医学领域中,需要建立更多的工程数学的虚拟仿真实验平台,应用于实验和教学中。
6 结语
目前大部分医学高校忽视了医学影像技术专业是理学科而并非是医学科,过分注重临床影像技术技能操作的培养,使得学生在物理原理和临床医学教育方面的知识都不系统,医工结合教育出现漏洞[16]。傅立叶变换相关知识是联系数学理论与成像理论的一个重要桥梁。基于虚拟仿真理念,融合“医工结合”发展趋势,创建一个面向医学影像技术专业学生的傅里叶变换虚拟仿真教学实验平台。该平台将傅里叶变换可视化,用一个个鲜明的曲线或图形展示出相关参数对波形的影响,旨在使学生对每一堂课的内容有感性认识,进一步激发学生的学习积极性与主动性,较好地培养他们的自主创新意识。该平台执行效率高、操作简单易行,仿真过程的可视化程度进一步提高,有利于数据的调试和优化。通过完善和改进,该平台还可以进一步优化和发展其他数学模块,提供更加丰富的实验教学内容。

