基于改进经验模态分解法和T-Copula的短期负荷预测

洪居华，林 毅，刘友波，余 希，郑 欢，蔡期塬

（1.国网福建经研院，福州 350109；2.四川大学电气工程学院，成都 610065）

0 引言

负荷预测有助于电网规划人员制定发电计划和需求响应计划，将电力生产成本降至最低［1］。负荷预测的精度能够影响规划成效，文献［2］中指出负荷预测误差降低1%，电力运营商的成本能节省9 000 万元。电网规划、投资和市场交易都是基于准确的电力负荷预测完成的，准确的电力负荷预测是保证电力系统安全、可靠、经济运行的前提［3］。

近年来，研究人员提出了许多模型来预测不同时段的电力负荷。根据预测时段的不同，这些模型可分为短期、中期和长期负荷预测模型［4］。短期负荷预测（Short-term Load Forecasting，STLF）模型能够预测未来几周的负荷，预测结果用于电力系统的短期运行计划，如发电计划。若要预测未来几个月到未来几年的负荷，则需要中长期负荷预测模型。基于模型体系结构，负荷预测模型主要分为两类：统计模型和数据驱动模型。传统的统计模型是使用线性回归函数建立的，其中STLF问题被视为时间序列预测问题［5］；回归模型是预测平稳时间序列的有效方法。然而，负荷需求具有非平稳性和非线性特征，因此近年来提出了数据驱动模型，主要在模糊逻辑［6］、人工神经网络［7］和支持向量机［8］的基础上完成。此外，准确地进行负荷预测还需要考虑气候（即温度、湿度等）、时间和社会经济约束［9］。为了提高预测精度，各种混合模型相继出现［10-11］。为了缓解传统经验模型分解（Empirical Mode Decomposition，EMD）的端部效应和包络限制，文献［12］中提出了改进的经验模型分解方法（Improved Empirical Mode Decomposition，IEMD）。

本文提出了一种新的混合型负荷预测模型［9-12］。为了补偿信号分解过程中的信息损失，引入T-Copula分析技术，将天气因素（即外生变量）的影响纳入到信号分解中。尽管IEMD能够克服传统EMD的局限性，但是只要将极值映射到边缘附近就可以得到很好的结果。考虑到峰值负荷预测精度的重要性，从拟合的Copula模型计算风险值VaR，以确定峰值负荷指示变量。此外，为外生变量确定了4 个峰值负荷指示变量，将这些变量作为负荷预测模型的输入，提高了高峰时段的负荷预测精度此外，深度置信网络（Deep Belief Network，DBN）克服了传统神经网络模型的不足，采用DBN对信号分解得到的数据进行处理。算例结果显示，本文提出的由IEMD、T-Copula和DBN组成的混合模型在考虑外部变量的情况下，能提供更高的负荷预测精度。

1 负荷预测建模思路

若将第m 天的负荷曲线表示为：Em（t） ＝［Em（1），Em（2），…，Em（n）］T，t ＝1，2，…，n。STLF模型能够得到Em（t）或者Em＋1（t）。

目前，混合模型由于具有较高的预测精度被广泛讨论。混合模型分为两大类，一类用不同的模型分别预测电力负荷［13］，根据权重值获得最终预测结果。文献［13］中分别采用BP神经网络、基于遗传算法的BP神经网络、小波神经网络、径向基函数神经网络、广义回归神经网络、支持向量机等不同的模型对电力负荷需求进行预测，基于此，应用花授粉算法对多目标模型的权重进行优化，通过加权平均确定预测值。另一类将电力负荷分解成若干分量，然后用恰当的模型［14］预测每个分量，最终预测结果为各分量预测结果之和。小波变换分解效率并不高，因此，近年来，EMD被广泛使用［10］。文献［10］中使用EMD将电力负荷分解为几个固定函数和一个残差函数，较好地预测了未来的负荷需求。其中，与EMD相关的端点效应和包络极限降低了信号分解的效率，降低了负荷预测的准确性，并且没有考虑外部变量的影响。基于此，本文提出一种综合IEMD、T-Copula和DBN的混合预测模型。

2 STLF混合模型构建框架

本文提出的STLF 混合模型框架如图1 所示，主要由负荷需求时间序列分解和外部输入变量的相关处理组成。IEMD能提高信号分解效率。根据T-Copula相关性分析计算出的风险值VaR，确定峰值负荷指示变量，将峰值负荷指示变量作为输入参数将提高峰值负荷预测的精度。

图1 STLF混合模型的框架

使用IEMD 产生固定函数的低频分量（IMF1、IMF2、IMF3等）和残差函数，相关步骤如下：

（1）利用IEMD将电力负荷需求时间序列分解为不同频率的多个子序列，即（IMF1、IMF2、IMF3等）和残差。

（2）将各IMF和残差作为DBN输入，得到各IMF和残差的预测结果。

（3）对输出结果进行加权平均，得到输出OP1。

采用T-Copula处理外部输入变量，计算能源负荷需求与4 个外部输入变量（如干球温度、湿球温度、露点温度和湿度）之间的上尾依赖关系。

（1）计算上尾相关参数λu＝［λ1，λ2，λ3，λ4］和对应的VaR。然后根据VaR1、VaR2、VaR3、VaR4确定每个外部变量的峰值负荷指示变量。

（2）使用负荷需求、相关参数和峰值负荷指示变量对每个DBN模型进行预训练。

（3）将每个DBN 获得的输出加权相加，得到输出OP2。

3 基于IEMD和T-Copula的STLF模型

3.1 时间序列信号分解

3.1.1 传统EMD方法

EMD通过不断迭代将信号分解成具有不同幅值的规则低频分量，包括固有函数IMF 和残差函数。IMF性质如下：对于每一个IMF，在整个长度上的极值和过零点的个数应相等或最多相差1 个；在任何区域，由局部极值定义的包络线平均值为零。为更清晰描述这两个特性，给出从E（t）中提取IMF的迭代过程：

（1）确定负荷需求时间序列E（t）的局部极大值（Emax（t））和局部极小值（Emin（t）），并利用三次样条曲线将它们连接起来构造上、下包络线。

（2）确定两个包络线的平均值与原始负荷需求时间序列之间的差异。如果上下包络线的平均值表示为g1（t），且E（t）＆与g1（t）之间的差定义为d1（t），则：

当d1（t）满足IMF的条件时，将它标记为I1（t），否则，重复上述步骤。

（3）确定残差

（4）重复上述过程，直到残差时间序列r1（t）是单调函数，即残差足够小，没有转折点。

（5）使用EMD分解，原始负荷可表示如下：

则数据由IMF和一个残差函数来表示。

EMD比小波变换、离散小波变换在分解复杂时间序列上更有优势，但存在以下问题［15］：传统EMD的端部效应会导致数据两端出现发散现象，末端极值无法确定为最大值或最小值，使包络线发生畸变，影响分解。例如，第1 个分解步骤出现误差，后一个分解动作将显示相同的结果失真。此外，三次样条插值会导致过调、负调现象，导致包络线不完整，从而影响结果。

3.1.2 IEMD方法

IEMD方法能够抑制末端效应和包络限制。为了抑制端部效应，采用线性外推法来确定包含给定数据集的最终数据。确定上包络线端点的过程如图2 所示。A、B为两个极大值，直线AB延伸到点C。如果交点C小于端点E的值，E 点被认为是上包络线的最大值，如图2 右端所示；如果C 大于端点E 的值，则点E被认为是上包络线的最大值，如图2 左端所示。同样地可以确定下包络线的端点。

图2 确定包络线最大值

传统EMD算法会使用三次样条函数计算信号的上下包络，然后计算平均值。三次样条曲线拟合的功率低，计算简单，但会产生超、负调现象，使包络偏离实际信号，形成不完全包络。为了解决三次样条曲线拟合的超、负调问题，许多学者提出了改进方法，如高阶样条函数法、多项式拟合法和分段幂函数插值法。本文对同一模拟信号采用非均匀有理B 样条插值与三次样条函数插值法相比较，发现前者得到了较好的结果。采用IEMD 后，信号分解结果如图3 所示。结果表明，IEMD算法可以将信号分解为不同的频率分量，不存在模式混合。

图3 采用IEMD进行信号分解的结果

3.2 T-Copula分析

初步研究表明，电力负荷与外部输入变量之间存在上尾依赖关系。Gumbel Copula 模型计算了电力负荷与4 个外部输入变量之间的上尾依赖关系。二元Gumbel Copula模型可以定义为：

式中：fx1（x1（t））和fE（E（t））表示边缘分布函数；x1表示一个外部输入变量；E表示系统负荷需求；f（x1（t），E（t））是二维联合分布函数；CP（x1，E）是Copula 函数。那么，确定每个外部变量的上尾相关参数：

最大似然估计可用于确定Copula 模型的参数α。由于系统负荷需求与外部输入变量存在非线性关系，采用基于样本的典型最大似然估计法进行处理。最大似然估计法的目标表示为

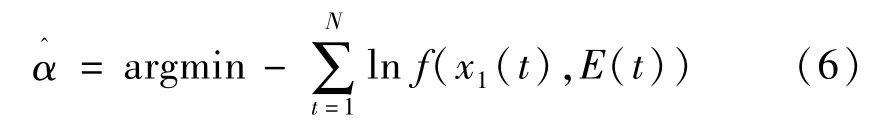
式中：N表示外部输入变量的数量。

Gumbel Copula的上尾相关参数λ1为

基于此，为所有外部输入变量确定所需的Copula 参数。由于电力负荷数据的波动和峰值的多样性，对峰值负荷进行有效的统计估计至关重要。本文引入阈值参数来确定各变量的峰值负荷指示变量，

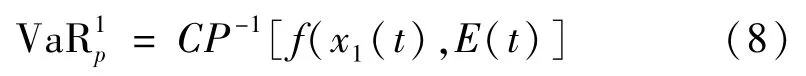
基于VaR 计算峰值负荷指示变量有助于提高高峰时段的负荷预测精度。

峰值负荷指示变量的二进制值由以下公式确定：

式中：M（x1）表示变量x1的峰值负荷指示性变量；p的值设置为0.95。对4 个外部输入变量进行计算。

Gumbel Copula模型确定了系统负荷与外部天气变量之间的上尾依赖关系。将信号的默认值设为0.05，通过最大似然估计对模型参数进行估计。图4给出了算例1 中系统负荷和外部气象变量之间的相关性，为便于分析，图中干球温度、露点温度、湿球温度、湿度、系统负荷已进行标准化处理，表示当前值与最大值的比值，无量纲，取值在［0，1］区间，如系统负荷0.5表示当系统负荷为最大可能系统负荷的0.5 倍的情况。

干球温度的尾部分布与尾部（0，0）点和（1，1）点有很强的相关性，干球温度对系统负载影响很大。为了考虑系统负荷与外部变量的正相关或负相关，本文给出了皮尔逊相关矩阵，如表1 所示。表1 说明系统负荷与干球温度、湿度正相关，与湿球温度、湿度负相关。在95%置信水平下进行VaR计算，上尾依赖参数和变量值如表2 所示。

图4 外部变量相关性分析

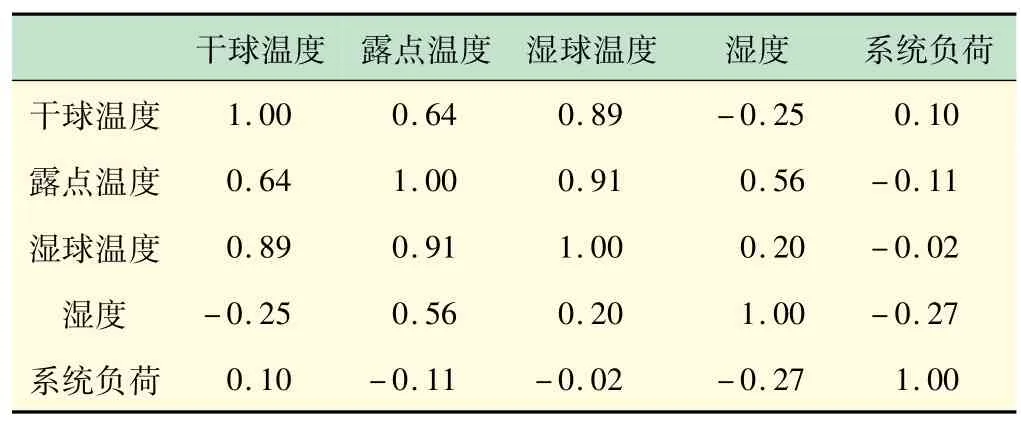
表1 系统负荷与外部变量相关性分析

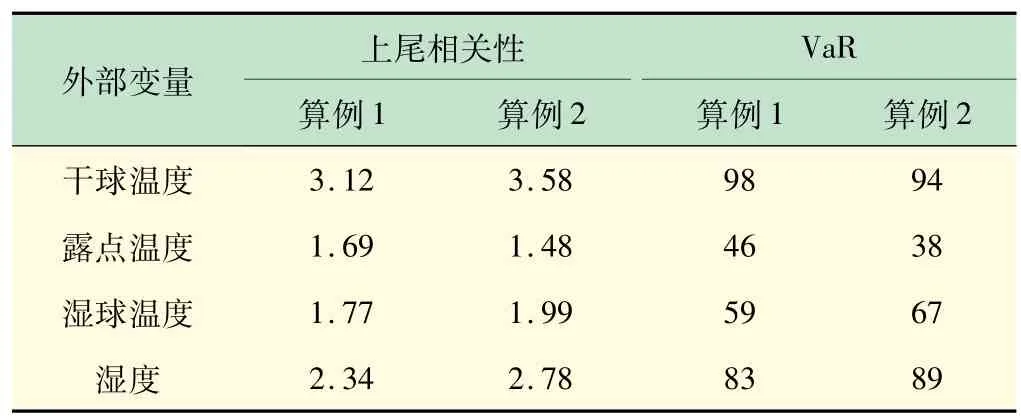
表2 具有外部变量的系统负荷的上尾相关参数和VaR

3.3 深度置信网络的实现

该方法通过IEMD 将负荷需求数据分解为多个IMF和一个残差。在相关性分析中，能够得到上尾相关参数，峰值负荷指示变量。将IMF、残差、上尾相关参数、峰值负荷指示变量和系统负荷数据应用于DBN。图5 给出了DBN的体系结构，每层单元之间没有相互连接。受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）是一种能够学习输入数据集上概率分布的神经网络［16］。DBN 预训练过程将神经网络中的每个连续组视为RBM，其联合概率为：

式中：h 表示隐藏层的输入；v表示从可见层获得的输出；W表示隐藏神经元的权重；a表示激活函数。对于每个RBM，都有一组隐藏层和可见层。

对于连续变量v的高斯-伯努利RBM为：

图5 深度置信网络结构示意图

RBM的目标函数为：

分层预训练要求DBN 在目标函数上遵循随机梯度下降法进行训练，参数（例如a、b、W）根据目标函数的梯度更新，如下所示：

式中：〈hi〉Ph｜v（h ｜v）是关于输入数据的条件分布的期望；〈hi〉recon是第i 次重构分布的期望。那么，参数更新如下：

训练多个层时，使用上层输出的条件期望作为下一层的输入，然后继续训练下一层。基于分层预训练方法，初始化DBN算法的所有参数。以监督学习的方式对参数进行调整，直到DBN 的损耗函数达到最小值。最后，将反向传播算法应用于调整过程。所有参数都从上到下更新，从而减少了预测误差。

为了识别负荷需求时序数据中的周期和模式，可以应用自相关函数选择具有相同信息特征的子集。假设时序数据集为E ＝Et，t∈T，滞后时间k 时的自相关系数rk计算如下：

4 算例分析

4.1 测试数据集

所提混合负荷预测模型在澳大利亚某地区数据集［17］和美国德克萨斯州某城市数据集［18］上进行测试。数据集主要包括：天气数据（即干球温度、湿球温度、露点温度和湿度）、时间分类数据（即小时、月、日）、社会数据（即工作日、周末、假日）和特定采样时间的负荷需求。

4.2 方法评估标准

平均绝对百分比误差（MAPE）和均方根误差（RMSE）用于评估不同模型的性能。

4.3 学习环境设置

对于基于信号分解的DBN，日前负荷预测与外部变量的相关性分析，取前1 天Et-48～Et-96负荷数据，以及前1 周所对同1 天Et-336～Et-348的负荷需求，作为DBN的输入。DBN 输入数量为100。上尾相关参数和峰值负荷指示变量也用于DBN 输入。通过交叉验证确定隐藏层的数目为3，每层隐神经元的数目为30，

DBN的结构为100-30-30-30-1。随机选择10%的原始数据进行交叉验证，根据结果将学习率设为0.1，迭代次数设为500 次。通过T-Copula 进行相关性分析时，默认阈值设为0.05。

4.4 实验结果分析

采用Matlab R2017b 进行了仿真，并对两个数据集进行了测试。对于这两个算例，使用下式将数据集线性缩放至［0，1］：

算例1收集了澳大利亚某地区2013-01-01～2013-12-31 日的数据［17］，采样时间为0.5 h。后文将全年数据分为4 个季节：1～3 月，4～6 月，7～9 月，10～12 月。周前负荷预测是将1 个月的3 周数据集作为训练数据集，剩余1 周作为测试数据集。假设每日信息可用，信号分解得到的输入数据集为8 个IMF 和残差。利用自滞后相关，将这些分解后的信号应用于配电网负荷预测。相关性分析得到的输入数据集包括上尾相关参数、二元峰值指示变量和根据学习环境设置得到的负荷需求数据集，基于DBN进行考虑外部变量的周负荷预测。对每个季节，采用2 个月的数据集来评估所提方法的负荷预测性能。

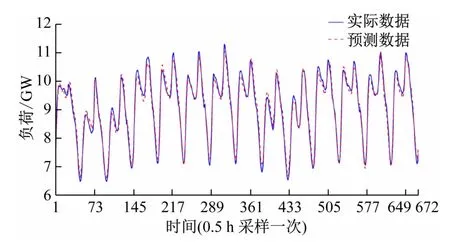
图6 提前两周的负荷预测结果

负荷需求预测结果如图6 所示，将该模型的预测结果与文献［10］进行比较，每小时的平均误差分布如图7 所示。从平均误差分布结果可以看出，高峰时段的负荷预测精度有所提高，这将有助于电力运营商制定正确的发电计划和运维计划。

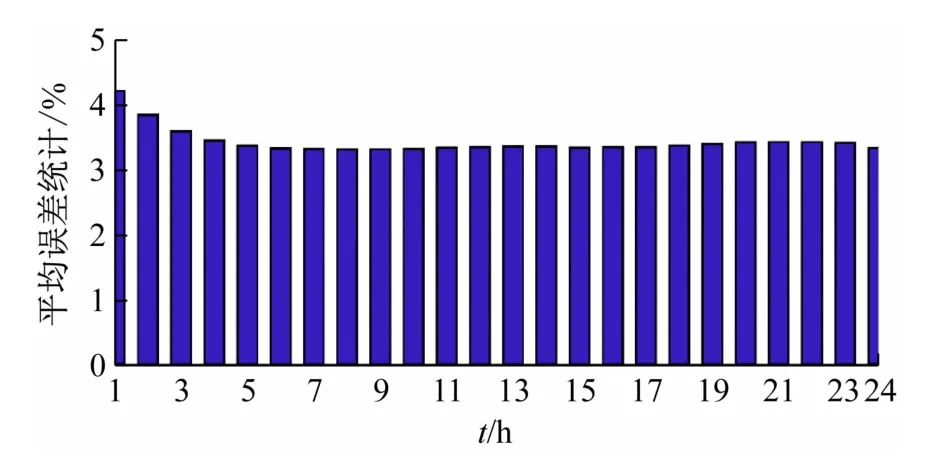
图7 误差分布

为了便于比较，对澳大利亚多个地区进行了模拟，如表3 所示。由表3 可知，所提模型与文献［10］中的方法相比，MAPE 值下降了21.19%，RMSE 值下降了16.93%，所提模型预测精度更高，说明IEMD 信号分解和T-Copula相关性分析能够提高预测精度。

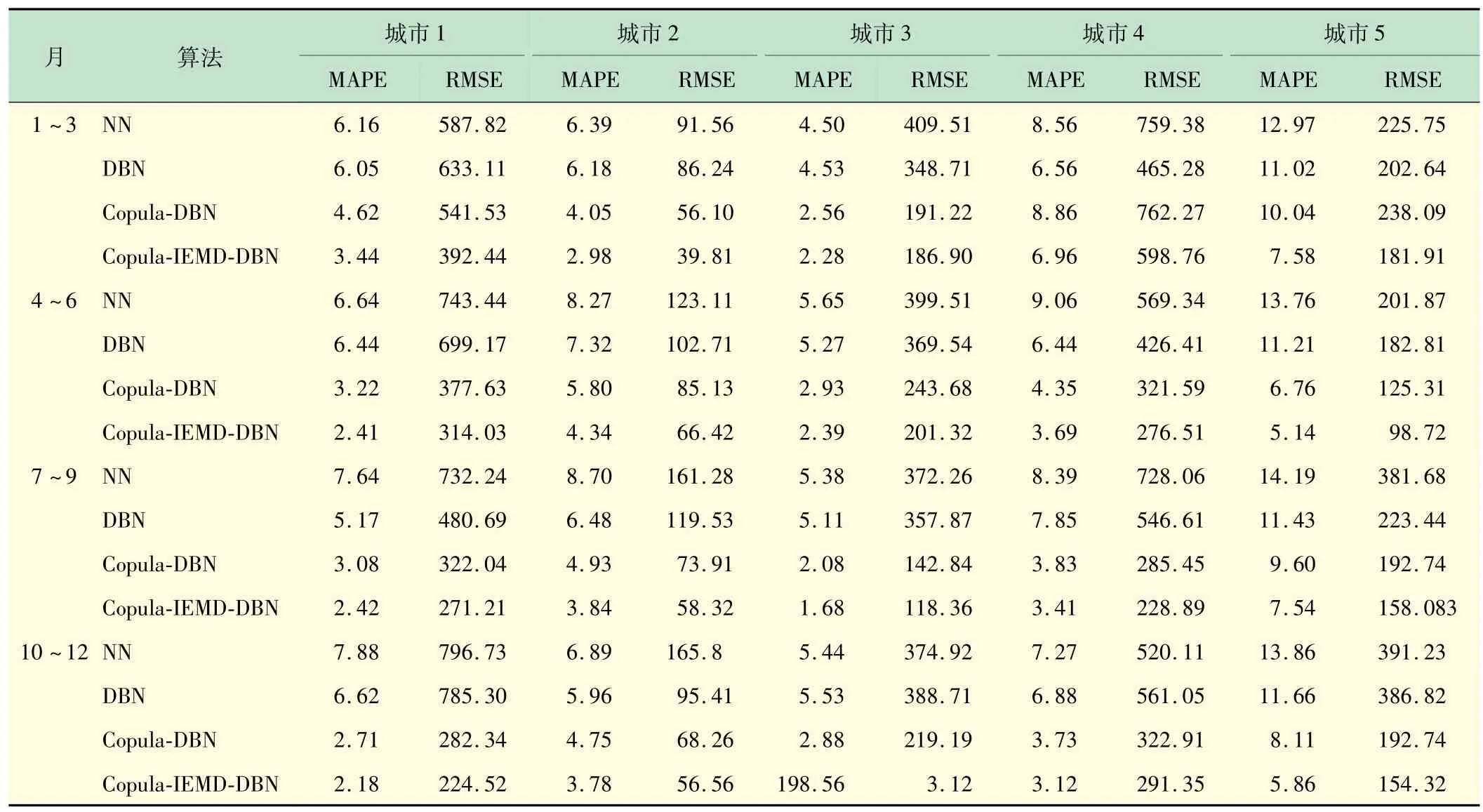
表3 算例1 的负荷预测性能比较

算例2基于美国德克萨斯州某城市2016-01-01～2016-12-31 的数据［18］，采样时间为1 h。如表4 所示，由于IEMD 和T-Copula 的联合作用，MAPE 和RMSE 值显著降低，该模型的MAPE 值下降了15.27%，RMSE值下降了13.86%。实际上，IEMD 通过计算VaR中的峰值负荷指示性变量，提高了信号分解效率，而T-Copula有助于提高高峰时段的负荷预测精度。

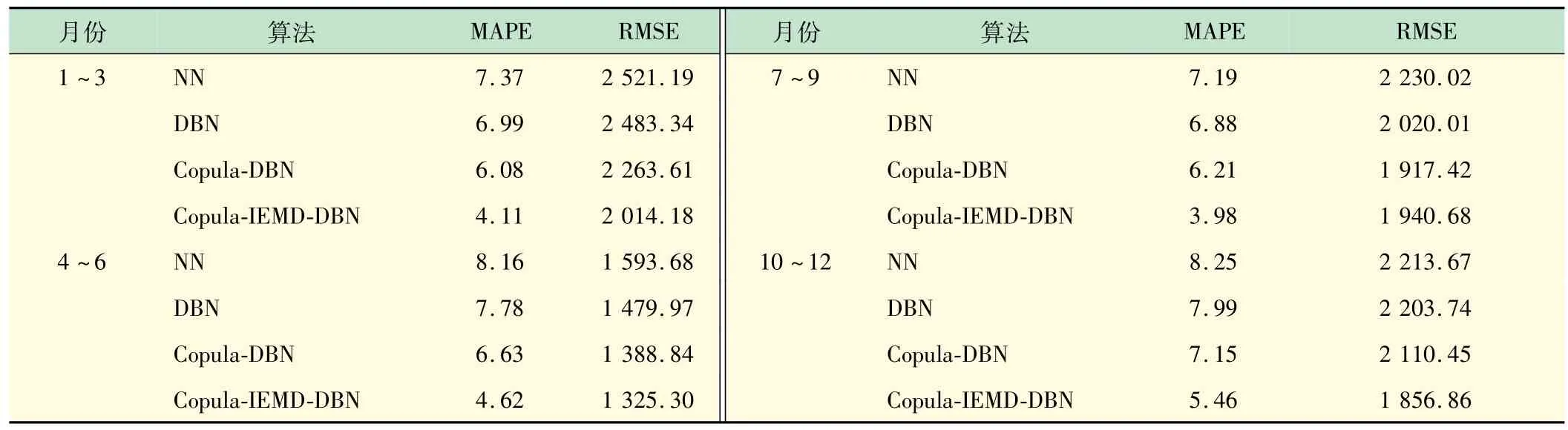
表4 算例2 的负荷预测性能比较

5 结语

本文提出了一种基于IEMD和T-Copula的混合短期负荷预测模型。首先，利用IEMD 对负荷需求时间序列进行分解；其次，采用T-Copula 进行系统负荷与外部输入变量的相关性分析，提高高峰时段负荷预测的准确性；然后，分别对两个分量进行预测；最后将各部分的结果相加，得到最终的预测结果。利用澳大利亚和美国电力负荷统计数据验证了该模型的有效性。结果表明：①IEMD 能更准确有效地提取电力负荷的线性和非线性分量；②通过T-Copula提高了高峰时段负荷预测的准确性；③DBN具有很好的处理电力负荷非线性分量的能力。结合每种模型的优势，混合模型可以捕捉到负荷多种特性，能够获得更准确的预测结果。此外，在混合模型中还可以加入一些未来可能的影响因素，如与需求响应相关的用户信息，以及分布式可再生能源集成带来的不确定性等。本文所提负荷预测模型对电网的短期发电、调度和运行提供一定的参考价值。