基于改进灰狼优化算法的积分计算实验

黄基诞

（1.东华大学旭日工商管理学院，上海 200051）

0 引言

科学计算和工程技术领域中，存在着各种数值积分的计算问题，比如桥梁设计、船舶设计、土地测绘等。目前，在数学领域中求解数值积分的方法有很多，经典的数值积分方法有牛顿-柯特斯公式（Newton-Cotes）法，辛普森求积公式（Simpson）法、梯形法、龙贝格求积公式（Romberg）、Gauss 法等［1］。但这些经典的方法在工程计算中都存在各自的不足，比如Romberg 虽计算精度高，但计算量大；Newton-Cotes 公式稳定性较差，收敛性得不到保证。近年来，随着计算机技术的飞速发展和许多新型的智能算法的出现，有学者开始逐渐利用或结合新型群智能算法求解数值积分，并取得了良好的效果。如人工鱼群算法［2］、粒子群算法［3］、细菌觅食算法［4］、差分进行算法［5-6］、蝙蝠算法［7］、神经网络算法［8］和生物地理优化算法［9］求解任意函数的数值积分，取得了较好的效果。

上述智能算法都在一定程度上解决了经典数值积分方法的不足，取得了较大的成功，为后续学者更深入的数值研究打下了扎实的理论基础。同时，目前国内外对群智能算法在求积分的数值解方面的研究属于起步阶段。本文将在前人的研究基础上继续深入拓展，改进灰狼算法用于求解数值定积分的方法，提出了结合Simpson3／8 公式的基于灰狼优化算法求任意函数的数值积分的方法。该方法的基本思路是：先在积分区间内产生一些随机分割点（不一定是等距分割点），然后用灰狼优化算法对这些分割点进行优化，将优化后得到的最优分割点从小到大排序并作为该区间的分割点，这些分割点结合Simpson3／8 积分公式进行数值计算，在这点上与以往的智能算法求解数值积分不同，以往的这些文献中的算法都是用的梯形公式；用本文方法求得数值积分不仅计算精度高，且对特殊函数如振荡函数同样适用。

随着科技的发展及新问题的不断出现，近些年涌现出一批新型的算法，如生物地理优化算法［9］，烟花算法［10］、引力搜索算法［11］等。这些算法优点就是能够快捷地给出接近最优的解.灰狼算法（Grey Wolf Optimization，GWO）最早是由Mirjalili等［12］于2014 年提出的，它是模拟自然界中灰狼群社会等级和狩猎行为的一种新型群体智能优化算法。该算法通过模拟灰狼跟踪、包围、追捕及攻击猎物等形式实现优化目的。灰狼算法具有数学模型简单、全局搜索能力强、参数设置少等优点，目前逐渐在调度领域得到应用［13-14］，背包计算问题［15］；还有学者将它用于光伏阵列局部阴影下最大功率点跟踪［16］。本文将对该算法的应用进行改进，将其用于求数值积分计算实验。

1 基本灰狼优化算法

GWO是通过数学模型模拟生物界中狼群捕猎机制与领导结构提出的一种新型群智能搜索方法。在灰狼种群中，根据领导地位和结构由高到低分级为：头领狼α，副头领狼β，普通平民狼δ，底层狼ω。该狼群群等级越低，则灰狼个体数量越多。狼群体在捕获猎物时，其他灰狼个体在头狼α 的带领下对猎物进行围攻。在d 维搜索空间中，第i只灰狼的位置记：

猎物的位置对应于优化问题的全局最优解。狼群猎食行动包括以下两个主要步骤：

（1）追踪及包围猎物。描述灰狼追踪并包围猎物的行为，满足如下公式：

式中：t表示当前迭代次数；X（t）表示第t 代灰狼个体的位置；Xp（t）为第t 代猎物位置，常数C 是摆动因子；常数A是收敛因子

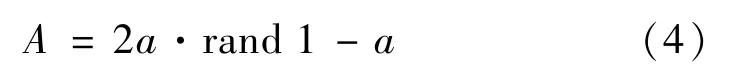
rand1，rand2 表示［0，1］之间的随机变量；变量a 称为随机因子，随迭代次数的增大从2 线性减小到0，数学表达为

（2）攻击猎物。当灰狼判断出猎物所在位置时，通常由头狼α引领β和δ发动捕猎攻击。因此狼群可以根据α、β、δ 三者的位置判断出猎物所在方向，进而更新灰狼位置：

式中：C1，C2，C3表示一个随机向量；X（t）表示当前灰狼位置向量。式（6）和（7）定义了ω狼朝向α，β，δ狼前进的步长和方向。然后由式（8）即可判断出个体向猎物移动的方向和ω 狼的最终位置［12］。尽管GWO算法得到了工程领域的广泛应用，但它和其他许多智能算法一样存在一些不足之处，比如求解精度低、易早熟等。

2 改进GWO求解数值积分

2.1 混沌种群初始化

GWO算法产生初始种群时是随机的，不一定均匀随机，故可能会影响种群的多样性。混沌序列是一种确定系统里经常出现的无规则杂乱运动，具有较强的遍历性，通常表现为随机情形下背后的简单规律。根据文献［17］中立方映射比Logistic和Tent映射产生的混沌变量更加均匀分布于区域之间，故本文采用立方映射产生混沌变量，应用于算法混沌初始化，即：

式中：－1 ≤zi（n）≤1，zi（n）≠0，n为迭代次数。由于混沌变量－1≤zi（n）≤1，zi（n）≠0，故需转换为改进混沌GWO 中第i 个灰狼每个维度的决策变量j位置。

为提高算法的全局搜索能力，提出混沌策略改进GWO，利用混沌动力学对算法的初始化过程进行改进。同时，为进一步提高种群的多样性，混沌序列产生初始序列的方式如下：

（1）随机产生N 个数据点zi（1），其中i ＝1，2，…，N，N为种群数量；每个分量的值为［－1，1］之间的随机数。

（2）分别以这些数据点为初始点按式（9）的混沌映射方式进行迭代，得到N 个混沌序列zi＝（zi（1），zi（2），…，zi（d）），d为问题维数。

（3）由于立方映射产生的序列中zi（d）的取值在－1 和1 之间，所以必须将其映射到灰狼的搜索区间中，映射规则如下：

式中：a和b分别表示搜索空间第d 维的上、下限，也就是积分区间。zi（d）是利用式（10）产生的第i 个粒子的第d维，则xik即为第i个灰狼在搜索空间第k 维的坐标。

2.2 单纯形差分扰动策略

为了提高GWO 的搜索性能，本文引入单纯形法策略进行扰动。在一次迭代完成之后，利用单纯形法搜索策略，选择底层ω 狼进行优化。找出最优点、次优点以及最差点，通过反射、压缩、扩张等操作更新最差点，形成一个新的多面体。它是一种局域的搜索方法。假设底层狼的位置为Xs，最优位置中心。

（1）反射操作

Xr为反射点，反射系数δ通常取1。

（2）扩张操作

Xe为扩张点，扩张系数φ通常取2。

（3）压缩操作

Xt为压缩点，压缩系数Ø通常取0.5。

（4）收缩操作

Xw为收缩点，收缩系数与压缩系数相同。

（5）差分进化算法特点收敛速度快、探索能力强，可以使新解朝着最优的方向进行搜索。差分操作如下：

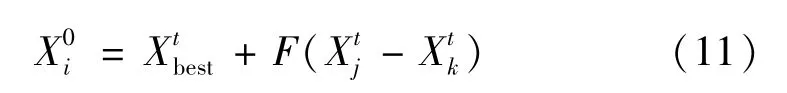
具体的单纯形差分扰动策略步骤设计如下：选取任意一个底层ω 狼的位置为Xs，分别计算出Xc，Xr，；比较这些目标函数值，并选取单纯形中的最优值与当前最优目标值进行比较。如果单纯形中的值更优，则替换X*。

2.3 改进GWO求任意函数数值积分

综上所述，本文提出的基于GWO 求任意函数数值积分算法流程可归结如下：

Step 1初始化基本参数a，A 和C、NP为种群个数、问题维数d 和最大迭代次数Tmax等参数；在被积区间内［a，b］根据混沌策略生成初始种群X ＝（X1，X2，…，XN），其中：Xi＝（Xi1，Xi2，…，Xin）；Xik∈［a，b］表示第k个节点，n表示积分区间内的节点数。

Step 2计算适应度并进行排序。先将随机产生的每个个体置于积分区间的左右端点之间，并按照升序排列，这样就得到n ＋2 个节点和n ＋1 小段，再分别计算这n ＋2 个节点相邻节点之间的距离dj，j ＝1，2，…，n ＋1 及这n ＋2 个节点对应的函数值和每小段中点对应的函数值，确定每小段左右端点和中间点的3个函数值中，记下最大函数值max Yj、最小函数值min Yj，j ＝1，2，…，n ＋1.并定义适应度为［7］

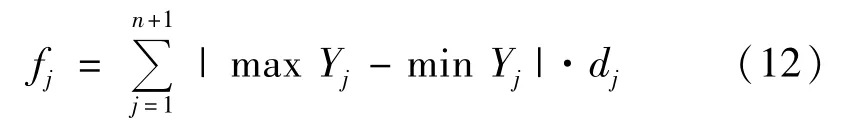
越小表明分割方法越好。

Step 3根据计算的适应度，得到当前的历史最优解Xα，次最优解Xβ，第3 最优解Xα和ω普通狼。

Step 4由式（6）计算群体中其他灰狼个体分别与α、β、δ狼的距离，并根据式（7）、（8）更新每个灰狼个体的位置。重新计算所有个体狼的适应度值并进行排序，更新最优值前3 的灰狼个体Xα、Xβ、Xδ的位置。

Step 5对底层狼ω 实施单纯形差分扰动策略，计算扰动后灰狼的适应度值并进行排序，若有改进重新找出3 个灰狼个体Xα、β、δ个体。

Step 6更新α、A和C等参数的值。

Step 7若未达到最大迭代次数Tmax，则返回步骤4；否则，输出全局最优位置；返回最优灰狼个体位置Xα，算法结束。

Step 8计算定积分值。将所求的最优分割点［α，x1，…，Xn，b］分别代入数值积分式进行计算（a ＝x0，b ＝xn＋1），得出：

3 数值实验

为了验证本文提出算法的有效性和正确性，选取了几个典型的数值积分函数，其中包括振荡函数，并着重与文献［6-7］中的方法进行比较。其中算法采用Matlab2015a 编程，实验运行环境为：CPU 2.6 GHz，内存4 GB，Windows7 操作系统（64 位）。

例1计算积分

该函数积分精确值为58.470 469 1［6-7］。文献［6］中给出用差分优化算法计算的结果值58.470 517 8；文献［7］中给出用蝙蝠优化算法计算的结果值为58.470 821 5；本文取N ＝15，D ＝100，运用灰狼优化算法计算结果为：

例2取N ＝20，D ＝60，分别计算6 个函数：x2，在积分区间［0，2］内的积分（见表1）。

表1 各算法对例2 的函数积分值比较

例3计算振荡函数积

该振荡函数积分的精确值为0.05［7］。文献［7］中给出的用蝙蝠优化算法计算的结果值为

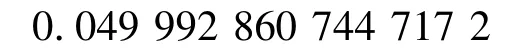
本文取N ＝20，D ＝120。运用灰狼优化算法计算结果：

例4计算振荡函数积

该振荡函数积分的精确值为－0.007 327 9［7］。文献［6］中给出的用差分优化算法计算的结果值为－0.007 332 8；文献［7］中给出的用蝙蝠优化算法计算的结果值为－0.007 335 411 855 213 67；采用本文灰狼优化算法时，针对被积函数的振荡性特点，分割点n取为200，其他参数设置不变。本文计算结果为：

4 结语

本文提出了用单纯形扰动和混沌映射方法改进灰狼优化算法结合Simpson3／8 积分求函数数值积分，对4 个不同数值积分算例进行测试。仿真结果表明，该算法收敛性、计算精度相比经典的数值积分方法优势比较明显，验证了灰狼优化算法改进的有效性和可行性。不仅对常用函数进行积分，还可以计算振荡积分等特殊情形，此方法是对经典求积分数值方法的一种有效补充。同时，也可作为灰狼优化算法应用领域的拓展应用。如何利用改进灰狼算法进行二重积分和三重积分计算，甚至利用灰狼优化算法计算常微分方程的数值解等问题可作为今后进一步研究的内容和方向。