指数有界双连续n阶α次积分C群的谱映射定理
2020-12-11 03:31:16赵华新周裕然
河南科学 2020年11期
周 阳, 赵华新, 周裕然
(延安大学 数学与计算机科学学院,陕西延安 716000)
算子半群的生成理论是算子半群的重要内容之一,许多学者对此作了大量的研究工作[1-3]. 文献[4-5]研究了双参数C 半群的一些结果. 文献[6]常胜伟、赵华新研究了局部有界双连续n 次积分C 半群的生成元及其性质. 文献[7]张明翠给出了n 阶α 次积分C 半群的概念、预解集以及次生成元等,并研究了相关问题. 文献[8]常胜伟等讨论了指数有界双连续n 次积分C 半群及其性质. 文献[9-11]讨论了相关半群的生成定理. 文献[12-15]研究了相关半群的谱映射定理. 本文在上述研究的基础上给出指数有界双连续n 阶α 次积分C 群的点谱,剩余谱,连续谱的定义并讨论了指数有界双连续n 阶α 次积分C 群谱映射定理.
1 预备知识
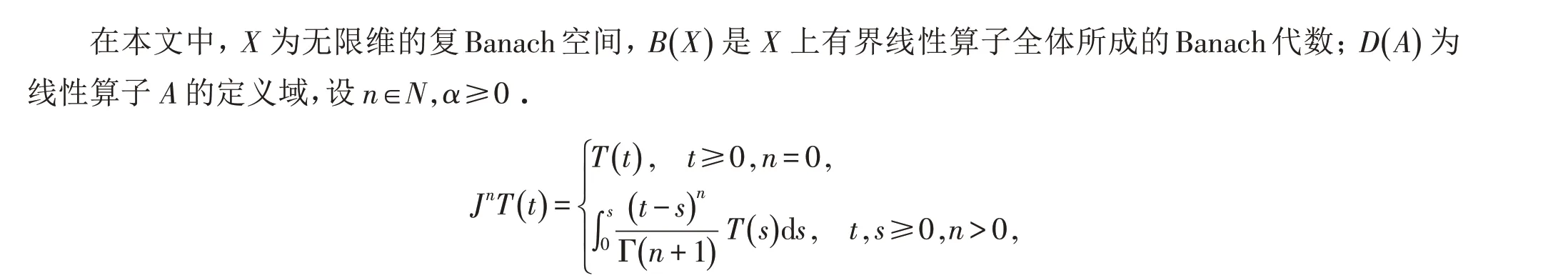
T=0 当且仅当存在n ≥0 使JnT( t )=0,t ≥0.
2 基本概念和引理

3 主要结果
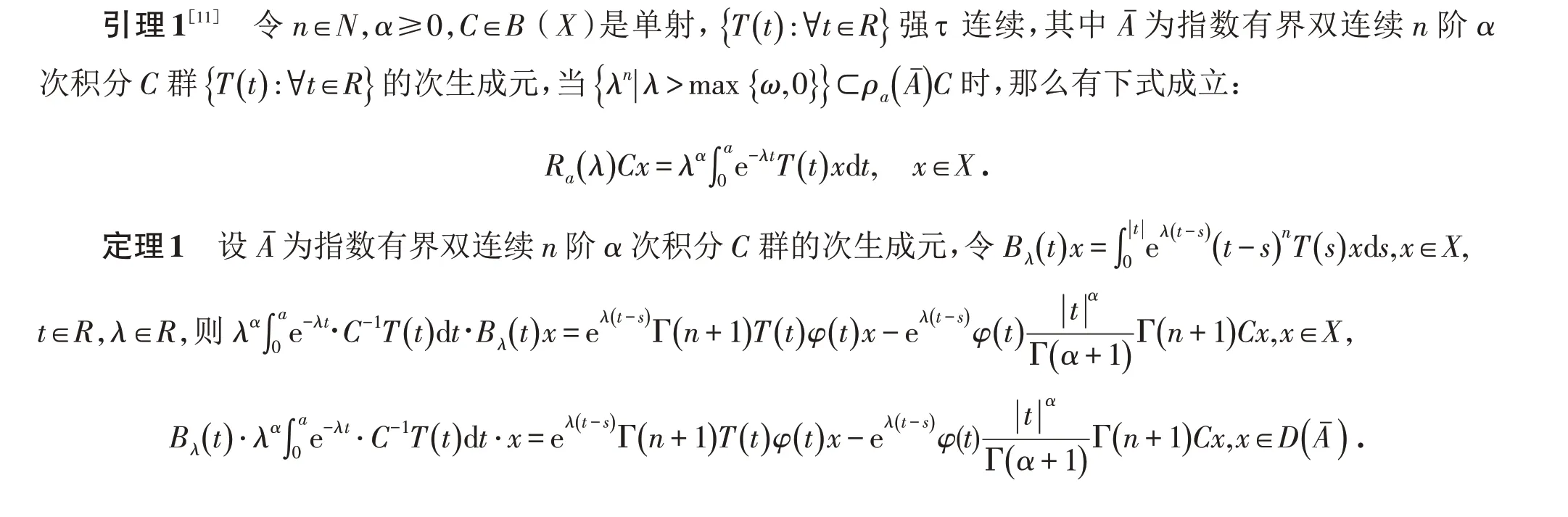
证明
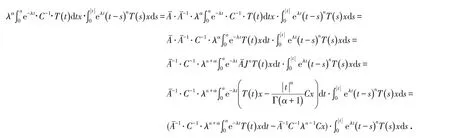
即
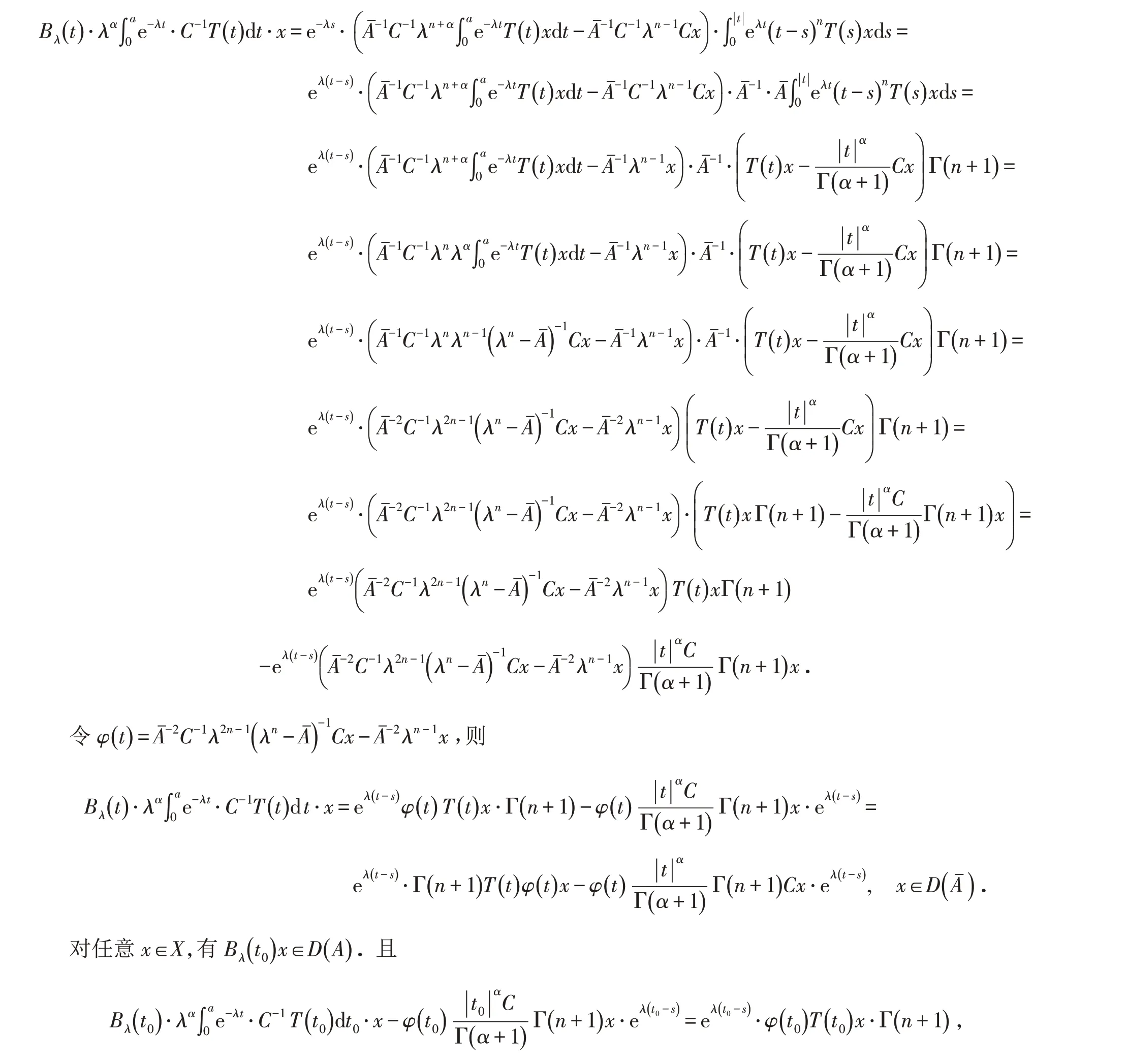


再证
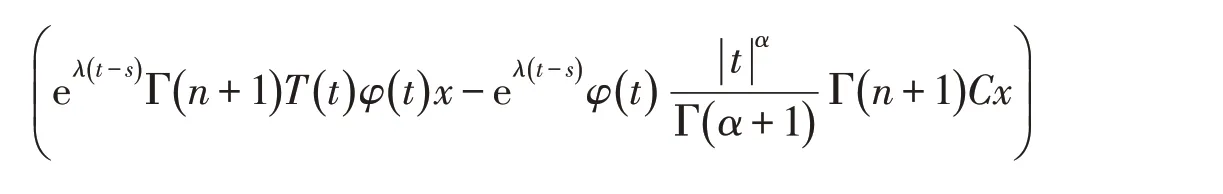
为单射,即
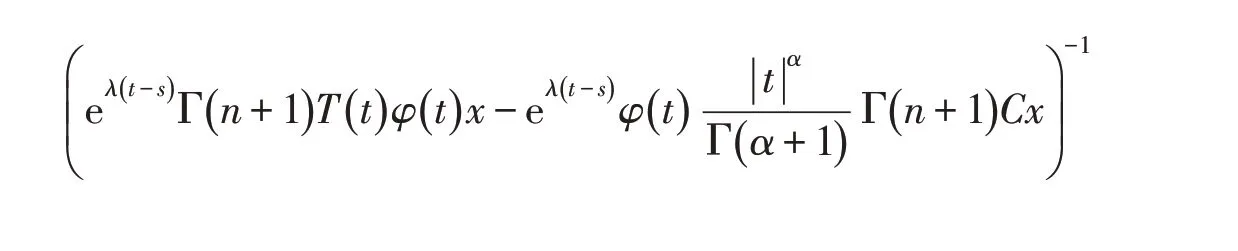
存在.
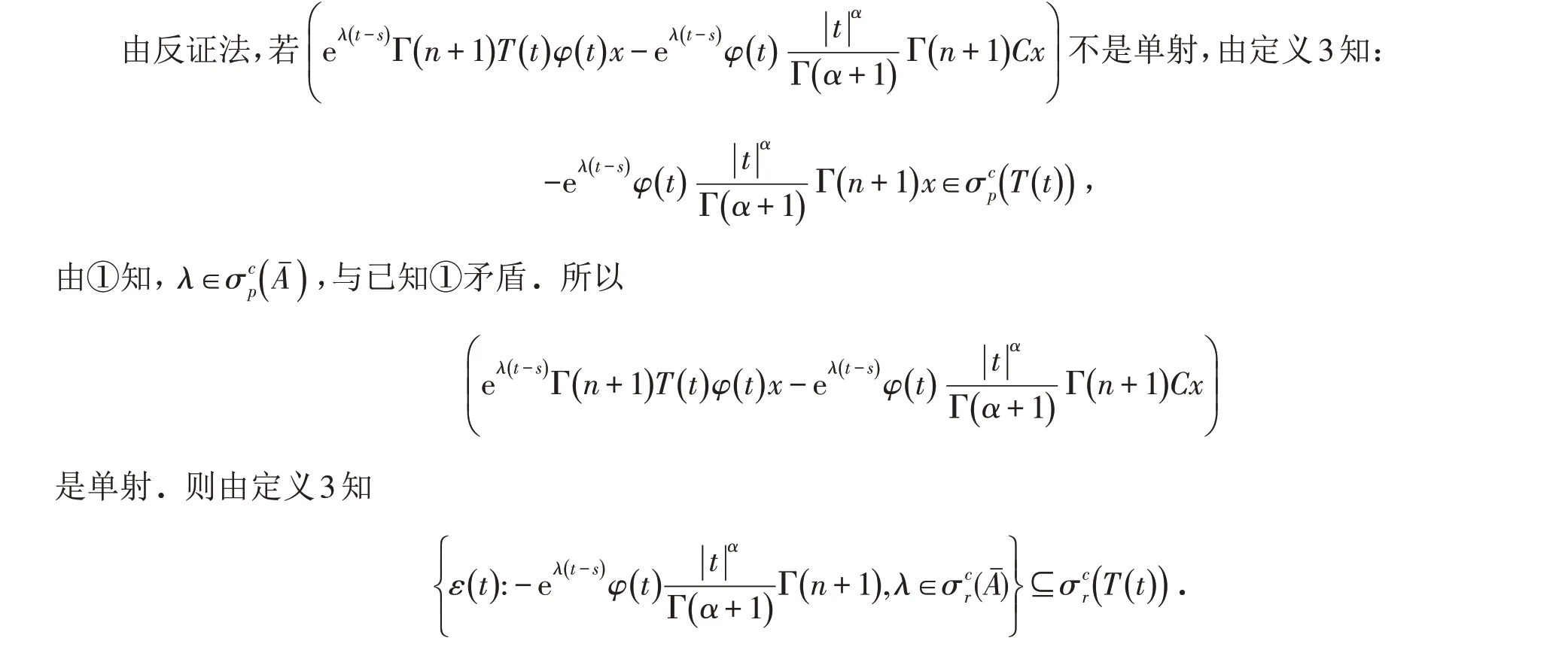
猜你喜欢
数学年刊A辑(中文版)(2023年4期)2024-01-04 05:47:40
四川师范大学学报(自然科学版)(2022年6期)2022-11-28 03:55:40
福建质量管理(2020年6期)2020-03-17 10:41:24
艺术家(2019年8期)2019-09-13 03:39:56
数学物理学报(2019年3期)2019-07-23 01:15:30
西南民族大学学报(自然科学版)(2019年2期)2019-05-17 05:42:48
情感读本·道德篇(2018年5期)2018-07-30 09:37:54
中华书画家(2016年6期)2016-10-26 01:09:19
福建中学数学(2016年4期)2016-10-19 05:09:02
乐府新声(2016年4期)2016-06-22 13:03:00

