PPP项目物有所值评价系统动力学模型应用

赵振宇，苑曙光，戴同，包格日乐图

(1. 华北电力大学 经济与管理学院，北京 102206; 2. 内蒙古建筑职业技术学院 工程管理学院，内蒙古 呼和浩特 010070)

社会资本和政府合作(PPP)参与公共基础设施的建设、运营和管理，提供公共产品服务，已成为公共基础设施项目开发的重要模式.近年来，我国已成为全球最大的PPP市场.根据现行规定，PPP项目需要经过物有所值评价、财政承受能力论证和初步实施方案(即“两评一案”)特别准入审批后，方可进入实施阶段.在审批决策过程中，物有所值(VFM)评价是判断项目是否适合PPP模式的重要依据，但由于PPP项目VFM评价涉及变量多、变量之间关系复杂，且变量具有动态性，加之PPP项目特许经营期较长，存在众多不确定性，增加了VFM定量评价的难度.因此，构建动态的PPP项目VFM定量评价模型，以准确反映VFM变化趋势，对PPP项目科学决策有重要的现实意义.

近年来，学者针对PPP项目VFM定量评价等的研究主要集中在两个方面：一是研究关键因素对PPP项目VFM量值的影响；二是通过构建具体项目VFM定量评价模型，实现VFM的准确测度.

在PPP项目VFM量值影响因素分析方面，薛朝改等[5]从政府、社会公众、社会资本三方角度引入系统动力学方法，分析影响PPP项目绩效的主要因素；崔彩云等[6]依据文献分析、专家访谈和德尔菲法构建PPP项目驱动因素层次结构模型，采用层次分析法(AHP)-决策试验与评价实验室(DEMATEL)方法确定VFM驱动因素重要性排序；Cui等[7]基于结构方程(SEM)构建PPP项目VFM驱动因素框架，分析各驱动因素之间的相互关系；Park等[8]对韩国3个大型公路PPP项目进行事后VFM评估，分析国债利率和折现率对VFM的影响；Liu等[9]运用因子分析法提取VFM评价指标，结合项目参数，提出一种熵权Pareto前沿定量决策方法.

关于PPP项目VFM的定量测度研究，现有研究主要集中在PPP项目风险的量化及关键参数的选取.在PPP项目风险量化方面，徐文等[10]采用改进的灰色关联度法确定PPP项目各项风险的损失权重，采用集值统计法确定各项风险的发生概率，并将二者结合进行项目风险成本的量化；荀志远等[11]以公立学校PPP项目为例，细化项目风险成本，通过指标量化确定项目的VFM值；梁玲霞等[12]建立风险量化评价指标体系，应用层次分析和专家打分法建立风险成本量化模型，构建城镇棚户区改造PPP模式VFM定量评价模型；郝德强[13]对资本成本率和现金净流量计算方法进行改进，构建适用于PPP项目VFM评价的净现值修正模型，使VFM量值计算更加精确；高华等[14]基于政府与社会资本方视角，研究PPP项目VFM评价中折现率的确定方法；Xu等[15]根据某PPP公路项目定价参数及风险因素，利用系统动力学方法建立项目特许权定价模型，并提出一种考虑不可量化风险因素的基于案例推理(CBR)的定价调整模型；Guo等[16]利用公共部门比较基准法构建VFM定量评价模型，对某城市轨道交通PPP项目融资模式的适宜性和具体运作模式进行定量评价.

现有VFM定量评价研究多为在一定特许经营期限条件下对项目物有所值的评价，鲜有考虑特许经营期内相关变量动态变化对VFM的影响程度.因此，迫切需要研究用以科学判定关键变量变化对PPP项目VFM影响的分析方法和有效工具.基于此，本文从系统动态性视角出发，根据PPP项目全寿命周期成本-收益构成，建立VFM定量评价系统动力学模型;然后,根据所建的模型，以某工业废渣处理PPP项目为案例，分析关键因素对VFM的影响，以帮助实现对项目的合理定价和特许经营合理期限的准确判断.

1 PPP项目VFM的计算

目前常用的VFM定量方法有公共部门比较值(PSC)法、成本效益法和竞争性投标法[17].PSC法由于适用性强，是应用最为广泛的评价方法，该方法是在假定采用PPP模式与政府传统投资方式产出绩效相同的前提下，比较两种采购模式下政府的净成本现值的偏差，即通过比较PPP模式下全生命周期内政府的净成本的现值(PPP值)与公共部门比较值(PSC值)，判断PPP模式能否降低项目全生命周期成本.PPP值(LCCPPP)与PSC值(PSCNPV)的计算式分别为

LCCPPP=NPVEI+NPVOS+NPVMI+NPVrisk,

(1)

PSCNPV=RVPSC+AVC+Crisk.

(2)

式(1),(2)中:NPVEI表示项目全生命周期内股权投资的现值；NPVOS表示生命周期内运营补贴的现值；NPVMI表示配套投入的现值；NPVrisk表示风险承担的现值;RVPSC表示PSC基准值，参照项目的建设、运营、维护的净成本；AVC表示竞争性中立调整值，主要指对政府部门所具有的一些固有优势和劣势进行调整；Crisk表示项目全部风险成本之和.

为了确保公共部门比较值与影子报价PPP值具有可比性，PPP项目VFM值的计算式为

VFM=PSCNPV-LCCPPP.

(3)

2 工业废渣处理PPP案例项目概况

G市位于我国西南地区，是全国最大的有色金属生产基地之一.长期以来，该市绝大多数从事有色金属冶炼的工厂将工业废渣集中露天存放，据统计，截止2015年底，G市累计堆存冶炼废渣量为3 500万t，其中，无序堆放量为2 000万t.2015年，G市有色冶炼企业一般废渣增量约为61万t，危险废物增量约为1.9万t；其他企业一般废渣增量约为1.2万t，危险废物增量约为3.1万t.2016年以来，随着对落后产能淘汰力度的不断加大，目前，G市需处置的新增废渣总量约为58万t·a-1.冶炼废渣中还有大量的重金属，对周边生态及群众健康造成严重威胁.根据当前区域危险固体废物防治的要求，为解决当地历史遗留的废渣处理问题，决定实施建设工业废渣集中处置场工程.

G市拟采用PPP和“设计-建造-运行-转让”(DBOT)方式建设一座838.8万m3的Ⅱ类一般工业固体废物填埋场，拟建项目特许经营期为15 a，含建设期1 a，总投资为33 812.56万元，其中，建设期投资29 055.53万元，建设期投资中包含工程的配套设施.项目由政府方发起，社会资本与G市国资公司共同组建项目公司，G市环保局与项目公司签订PPP项目合同，授予项目公司投融资、设计、建设、运营管理、维护并移交项目.资本金拟为20 250万元，其中，政府出资8 250万元，社会资本出资12 000万元.项目采用使用者付费模式，根据同类项目产品售价预测本项目堆渣收购价格为71.2元·t-1，特许经营期间，收费标准可根据政府最新出台的指导价格及当地物价浮动指数进行综合调整.根据项目公司收益情况，政府方和社会资本方按股权比例共享项目公司收益.

根据调研，历史存量废渣需送至堆场集中堆存的量约为630万t，结合现有废渣产生量，拟建渣场入堆渣量如下：第1～5年为108.2万t·a-1；第6年以后为34.1万t·a-1.本项目运营成本主要包括管理费和废渣处置费用，其中，废渣处置费用含废渣运费、处理费及填埋费.废渣运费、处理费和填埋费分别按22,24,21元·t-1测算.项目适用的增值税税率为6%，附加税含城市建设附加税、教育费附加税及地方教育费附加税的税率，它们分别为7%,3%,2%，企业所得税税率按15%测算.由于本项目为DBOT，建设期形成的固定资产所有权不归项目公司所有，因此,不计固定资产折旧，在特许经营期内长期使用的运营性资产计入摊销.项目运营期内融资成本率按中国人民银行同期贷款基准利率上浮10%，按等额本息法还本付息.

3 工业废渣处理PPP项目VFM系统动力学模型

系统动力学(system dynamics)是基于系统工程理论，研究系统内部结构与动态行为关系的重要方法，尤其适用于分析经济、社会等非线性复杂系统问题[3].PPP项目物有所值VFM计算涉及多个变量，这些变量与项目建设期投资、运营维护成本、税费、运营补贴、特许经营期、折现率等多个因素存在着相互作用和联系.由于PPP项目VFM属于非线性动态性反馈系统，因此，选择应用系统动力学方法，根据项目投资收益各相关变量构建VFM净现值模型.

根据式(3)，PPP项目VFM主要涉及PPP和PSC两个子系统，根据上述工业废渣处理PPP案例项目特点，对两个子系统的要素进行描述，如表1所示.

根据表1变量间的关系构建PPP项目VFM定量评价因果关系图，如图1所示.图1中：箭头前端的“+”和“-”表示相链接的两变量变化方向一致和不一致.

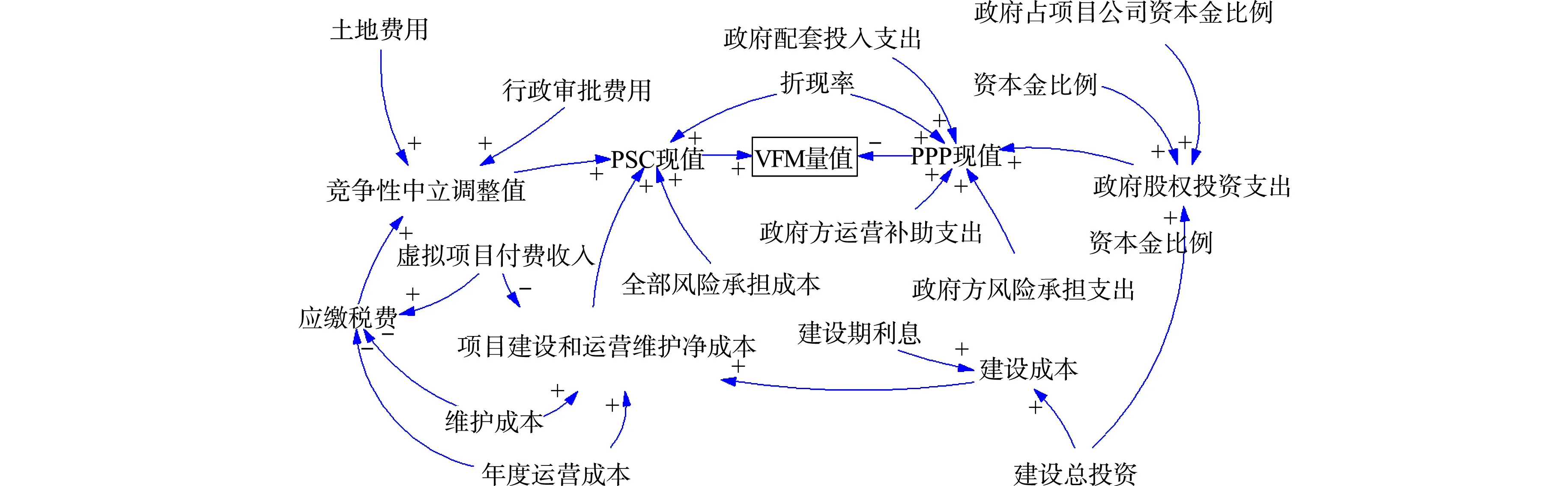
图1 PPP项目VFM量值系统动力学因果关系图Fig.1 Causal diagram of VFM evaluation system dynamics of PPP project

在PPP项目VFM定量评价因果关系分析的基础上，结合文中PPP案例项目中VFM变量关系，构建该项目物有所值VFM定量评价系统动力学模型.工业废渣处理PPP案例项目VFM量值系统动力学存量流量图，如图2所示.

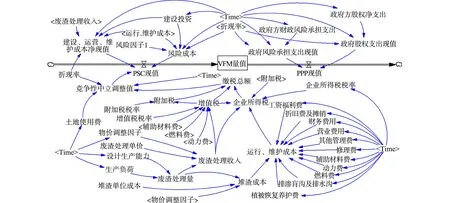
图2 工业废渣处理PPP案例项目VFM量值系统动力学存量流量图Fig.2 Stock flow chart of VFM evaluation system dynamic for industrial waste disposal PPP case project

工业废渣处理PPP案例项目VFM系统动力学模型由PSC现值与PPP现值两个子系统组成.VFM量值系统动力学模型参数设置,如表2所示.表2中：风险因子1指项目全部风险成本占项目建设运营成本的比例，文中按文献[11]取值.

表2 VFM量值系统动力学模型参数设置Tab.2 Parameter setting of VFM evaluation system dynamics model

4 工业废渣处理PPP项目基准场景VFM量值测度

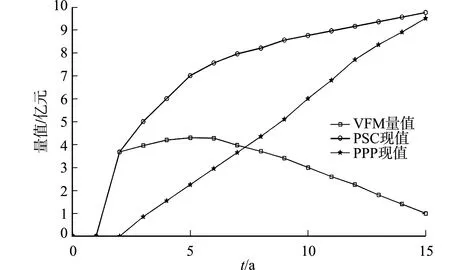
图3 工业废渣处理PPP案例项目 VFM，PPP和PSC变化趋势Fig.3 Change trend of VFM, PPP and PSC of PPP project of industrial waste disposal

由于案例项目运营期为15 a，含建设期1 a，因此，运营期开始的时间点为第1年末，仿真的各现值数据设定特许经营期的第1年末为折现点、第15年末为折现结束点.假定折现率为8%，贷款利率为5.39%.将工业废渣处理案例项目及参考数据输入PPP项目VFM定量评价系统动力学模型中，对案例项目的PPP现值、PSC现值和VFM量值计算过程进行仿真模拟，结果如图3所示.图3中：t为特许经营期.

由图3可知：项目物有所值定量评价中，PSC现值与PPP现值均随特许经营期的延长而呈上升趋势，PPP现值的初始值远低于PSC现值，但PPP现值的上升幅度大于PSC现值的上升幅度；由于在第2～6年处理历史存量废渣和新增废渣，生产负荷为最大值，从第7年起仅处理新增废渣，因此，PSC现值曲线在第7年以后上涨趋势逐渐变缓；同时，VFM量值随着特许经营期的延长呈逐年降低趋势，且在特许经营期的第15年趋于0，接近于物有所值定量评价的临界点.根据分析结果可知，在现有设定条件下，对于政府方而言，第15年的VFM量值大于0，因此，本项目物有所值.

5 工业废渣处理PPP项目VFM敏感性分析

5.1 生产负荷变化对VFM的影响

大多数市政工程PPP项目在建成后的运行负荷比较稳定(如污水处理项目)，但工业废渣处理项目的生产负荷受上游产业影响较大，特别是与高耗能、高污染的企业配套的固体废料处理项目，其上游产能受国家及地方政策调整影响很大，生产负荷难以预测.针对G市废渣处理项目未来生产负荷，可依据不同场景进行预测.除前文预测的基准场景外，还有以下3种不同场景.

1) 低负荷场景.设定历史存量废渣处理量与基准场景一致，仅处理630万t历史存量废渣，但预测未来产业结构发生调整，上游企业废渣生产量以1%的速度逐年递减.

2) 中等负荷场景.设定历史存量废渣处理量及年新增工业废渣量与基准场景一致，但预测未来项目公司市场运营得当，将周边县市的其他废渣垃圾也运至项目填埋，使项目在第7～15年内每年的负荷率上升2%.

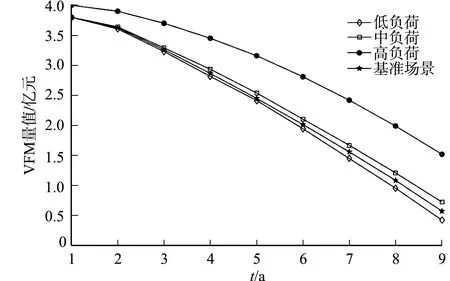
图4 不同负荷场景下工业废渣处理 PPP案例项目的VFM量值Fig.4 VFM of industrial waste disposal PPP case project under different load conditions

3) 高负荷场景.设定上游企业生产废渣水平与目前一致，但G市未来持续加大环境治理力度，不仅当年产生的废渣需处理，G市历史产生的无序堆放的2 000万t废渣也要在特许经营期内处理.假定在高负荷场景下，第2～6年，每年处理存量废渣108.2万t;第7～15年，每年处理存量废渣104.21万t.

针对上述3种场景，利用PPP项目VFM定量评价系统力学模型进行模拟仿真.不同负荷场景下工业废渣处理PPP案例项目的VFM量值，如图4所示.

由图4可知：在特许经营期末，高负荷场景的VFM量值远大于其余两个场景，中等负荷场景和低负荷场景的VFM量值差异较小.结果表明，未来政府部门处理历史存量废渣的政策对项目VFM量值的影响较大，如果仅处理现有计划的670 万t存量废渣，未来项目生产负荷的小幅波动对项目VFM量值影响较小.

5.2 折现率变化对VFM的影响

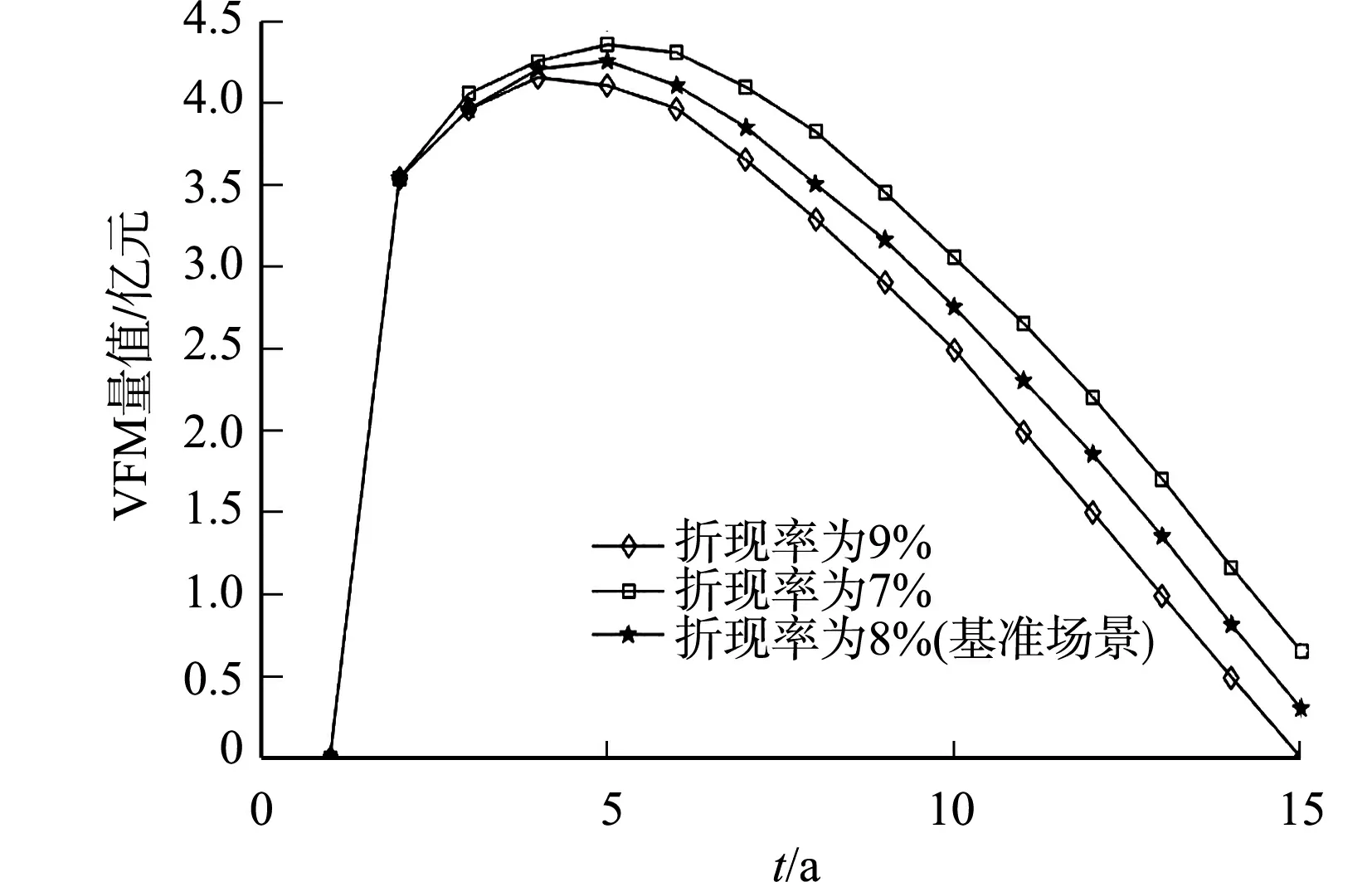
图5 不同折现率下工业废渣 处理PPP项目的VFM量值Fig.5 VFM of industrial waste disposal PPP project under different discount rates

在PPP项目VFM定量评价过程中，对政府方而言，关键且较难确定的影响因素是折现率.在工业废渣处理PPP案例项目中，借助VFM系统动力学模型可对折现率的敏感性进行分析，假设废渣处理单价为71.2元·m-3，生产负荷与基准场景一致，分别选取折现率为7%,8%,9%三种情形，利用PPP项目VFM定量评价系统力学模型模拟VFM值的变化趋势.不同折现率下工业废渣处理PPP项目的VFM量值,如图5所示.

由图5可知：随着折现率的提高，特许经营期末的VFM量值逐渐下降；当折现率为9%时，特许经营期末的VFM等于0.因此，从政府决策角度，如要保证项目物有所值，该项目的折现率取值应小于9%.

5.3 处理单价变化对VFM的影响

由于PPP项目涉及政府、社会资本及使用者，PPP项目定价是影响三方利益的关键，合理的定价标准是体现PPP项目公益性的保证，因此，分析价格与VFM之间关系尤为重要.

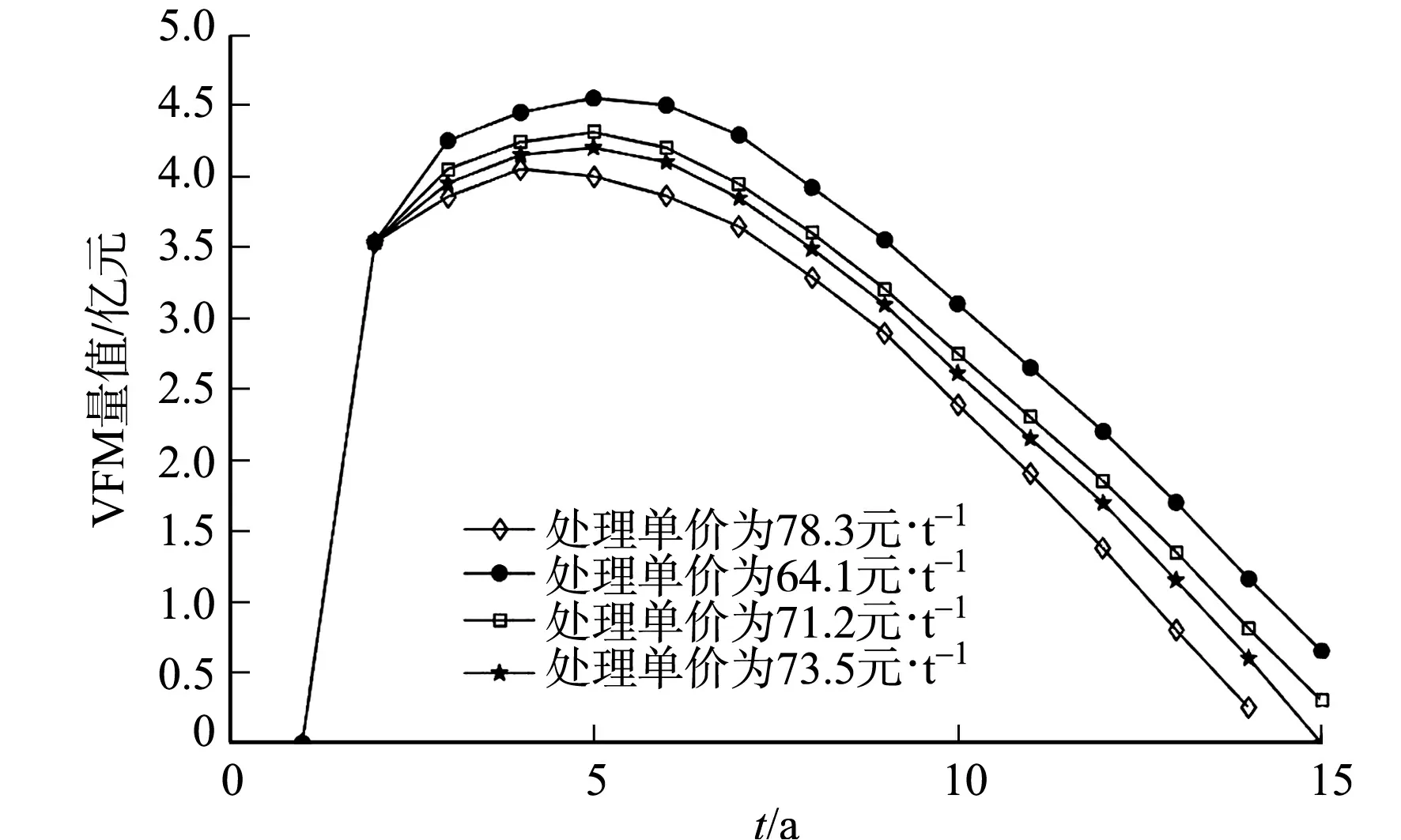
图6 不同单价下工业废渣 处理PPP项目的VFM量值Fig.6 VFM of industrial waste disposal PPP project under different prices

运用基于系统动力学的PPP项目VFM系统动力学模型，分别将废渣处理单价设为合同价(71.2元·t-1)、合同价上浮10%(78.3元·t-1)、合同价下浮10%(64.1元·t-1)，模拟废渣处理单价对项目VFM量值的影响，根据模拟结果可进一步判断满足VFM量值大于0的最低处理单价水平.废渣处理单价在特许经营期内对PPP项目的VFM量值影响，如图6所示.图6中:处理单价为73.5元·t-1时，废渣处理PPP项目在第15年的VFM量值为0.

由图6可知：随着废渣处理单价的提升，项目VFM量值呈下降趋势；当处理单价为73.5元·t-1时，第15年时的VFM为0.由此可判断，当废渣处理单价取78.3元·t-1时，项目特许经营期末VFM值将低于0，从政府决策的角度，特许经营期缩短至14年比较合理.因此，为了充分发挥PPP项目的社会服务作用，在其他参数不变的情况下，该项目初始的废渣处理单价不应高于73.5元·t-1.

6 结束语

PPP项目VFM量值的影响因素众多，且在项目生命周期内动态变化，为了能够动态分析VFM量值的变化过程，以PSC法为基准，根据PPP项目全寿命周期成本-收益构成要素的关系，利用系统动力学方法，构建PPP项目VFM系统因果关系模型及系统动力学定量评价模型.以某工业废渣处理PPP项目为案例，利用VFM系统动力学定量评价方法对项目的VFM变化趋势进行仿真，并分析VFM关键参数对VFM量值的影响.研究结果表明，对于固废处理PPP项目，在未来不同环保政策情况下，项目VFM量值存在较大差异；在一定生产负荷水平下，为保证项目物有所值，折现率和处理单价均存在理论上限值.文中提出的方法可以精准反映PPP项目特许经营期内VFM量值的变化趋势，并能够用于决策变量的敏感性分析，为PPP项目物有所值定量评价提供了一种新型实用工具.相比传统的VFM计算方式，基于系统动力学的VFM分析方法有着调整数据简便、结果清晰、指导性强的优点，具有良好的应用推广价值.