无刷直流电机DSP逻辑控制程序的Petri网设计方法
詹瑜坤,孙佳伟,罗继亮,郑力新,张兵
(1. 华侨大学 信息科学与工程学院,福建 厦门 361021; 2. 华侨大学 福建省电机控制与系统优化调度工程研究中心,福建 厦门 361021; 3. 华侨大学 工学院,福建 泉州 362021; 4. 南阳农业职业学院 机电工程系, 河南 南阳 473000)
电机等设备的逻辑控制程序需要人工反复调试和检测,非常费时、费力[1],而且难以避免程序中的逻辑错误,例如,英国希思罗机场行李分拣系统事故[2].因此,需要研究逻辑控制程序的形式化设计方法,从而有效地减少控制程序设计和调试的时间,节约人力成本[3-4].
Petri网是一种描述离散事件系统的形式化语言,适合描述数字硬件电路,尤其是异步或自动定时电路.文献[5]给出一种将Petri网翻译为布尔方程的方法,从而利用Petri网和布尔代数设计逻辑控制器.文献[6]利用Petri网及其关联矩阵,给出现场可编程门阵列(FPGA)逻辑控制器的设计方法.文献[7-8]给出基于Petri网的可编程逻辑控制器(PLC)程序设计方法.文献[9-10]提出基于输入输出Petri网的无刷直流电机FPGA逻辑控制程序的设计方法,将噪音滤波器、正交解码器、脉冲宽度调制(PWM)生成器和无刷直流电机换相管理器描述为Petri网结点,利用网结构刻画各功能模块的复杂关系,确保逻辑的正确性和可靠性,并利用Petri网设计电机的超高速硬件描述语言(VHDL)控制程序.基于普通Petri网,本文提出一种无刷直流(BLDC)电机数字信号处理(DSP)逻辑控制程序的设计方法.
1 基本概念
普通Petri网是一个三元组N=(P,T,F),P为库所集,T为变迁集,F为库所和变迁之间有向弧的集合.设m(p)为库所内的托肯数;m0为初始标识;·t为变迁t的所有输入库所集;t·为变迁t的所有输出库所集.如果∀pi∈·t,当m(pi)≥1时,标识m下变迁t是使能的;如果t激发,则托肯从输入库所跃迁到输出库所,得到后继标识m′.
可达图以有向图的形式描述Petri网的动态行为,每个结点表示Petri网的一个可达标识,结点之间用一条有变迁标记的有向弧相连,它描述了弧的终点标识是由弧的起点标识通过激发该变迁得到的.可达图生成算法是根据Petri网的激发规则计算其可达图的计算方法[11],主要有以下4个步骤.
步骤1将初始标识m0标记为一个新结点.
步骤2任意选择一个新结点m,激发m对应标识下每个使能的变迁t,如果生成的标识m′在可达图中没有出现过,则将m′标记为一个新结点,并画一条从m到m′的有向弧,该弧上标记变迁t.
步骤3将结点m标记为旧结点.
步骤4如果可达图中存在新结点,任意选择一个新结点,记作m,执行步骤2;否则,算法退出,输出可达图.
无刷直流电机驱动电路,如图1所示.图1中:VT1~VT6为功率管;D1~D6为二极管;AA′,BB′,CC′为无刷直流电机定子的三相电枢绕组.无刷直流电机的驱动电路主要由6组功率管构成,功率管根据两两导通(表1)的规则控制通断,通过霍尔传感器检测转子位置,控制器处理位置信号,输出换相信息,驱动逆变电路3个桥臂上的功率管VT1~VT6[12-15].
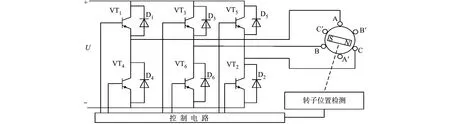
图1 无刷直流电机驱动电路Fig.1 BLDC motor drive circuit
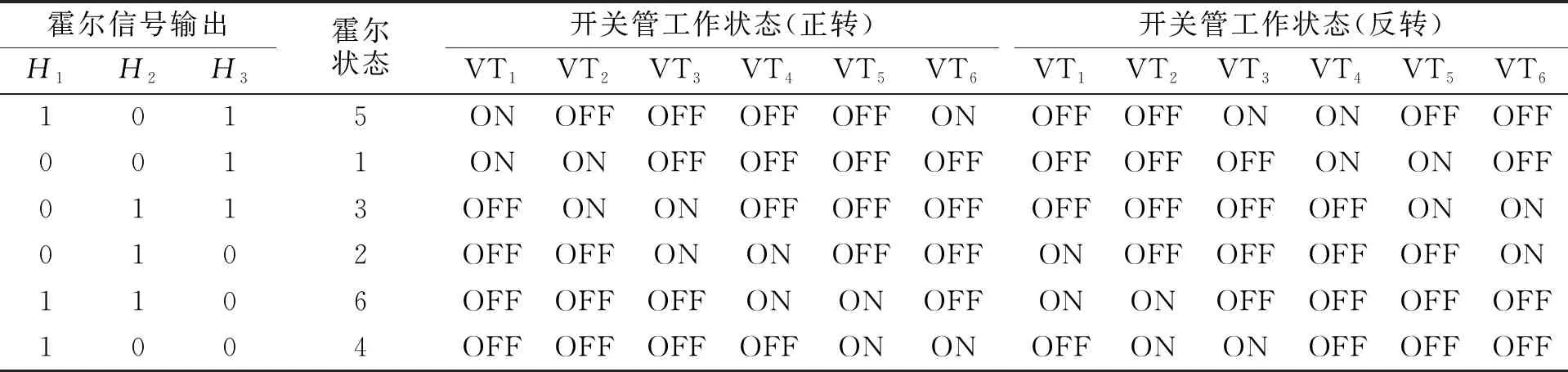
霍尔信号输出H1H2H3霍尔状态开关管工作状态(正转)VT1VT2VT3VT4VT5VT6开关管工作状态(反转)VT1VT2VT3VT4VT5VT61015ONOFFOFFOFFOFFONOFFOFFONONOFFOFF0011ONONOFFOFFOFFOFFOFFOFFOFFONONOFF0113OFFONONOFFOFFOFFOFFOFFOFFOFFONON0102OFFOFFONONOFFOFFONOFFOFFOFFOFFON1106OFFOFFOFFONONOFFONONOFFOFFOFFOFF1004OFFOFFOFFOFFONONOFFONONOFFOFFOFF
2 无刷直流电机逻辑驱动电路的Petri网建模方法
无刷直流电机逻辑驱动电路的Petri网建模包括两个部分:一是建立无刷直流电机驱动电路的被控Petri网模型;二是建立控制电路的Petri网模型.建立无刷直流电机驱动电路的被控Petri网模型是为建立控制Petri网切换提供前提条件.
算法1无刷直流电机驱动电路的被控Petri网模型设计方法.
输入:霍尔信号Hi(1≤i≤3);电机旋转方向控制变量D
输出:驱动电路的被控Petri网模型Np=((Pp,Tp,Fp),m0)
1:Pp=∅,Tp=∅,Fp=∅
2:for allHido
5: end if
6: end for
7:forDdo
10: end if
11: end for
霍尔传感器和电机旋转方向控制变量的Petri网模型,如图2所示.

(a) 霍尔传感器 (b) 电机旋转方向图2 霍尔传感器和电机旋转方向控制变量的Petri网模型Fig.2 Petri net models of Hall sensors and control variables of motor rotation direction
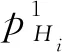
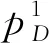
算法1的输入变量包括3个霍尔传感器和1个电机旋转方向变量,为每个输入变量设计2个库所和2个变迁结点,总计8个库所和8个变迁结点,因此,其时间复杂性是输入变量个数的多项式,即其复杂性是多项式级的.
算法2驱动电路的控制Petri网模型设计方法.
输入:被控对象的Petri网模型Np=((Pp,Tp,Fp),m0)和逆变电路两两导通切换规则
输出:驱动电路的控制Petri网模型Nc=((Pc,Tc,Fc),m0),1≤i≤6
1:Pc=Pp,Tc=Tp,Fc=Fp
2:for all VTido
6: end for


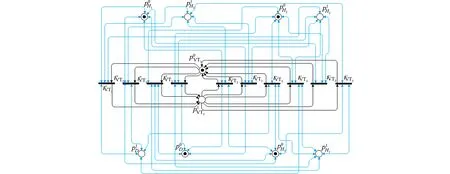
图3 功率管VT3的控制Petri网模型Fig.3 Controlled Petri net model of MOSFET VT3
在驱动电路中,功率管是控制电流通断的执行器件,算法2设计了功率管通断逻辑的Petri网模型,以描述驱动电路的控制执行逻辑.算法2具有6个功率管输入变量,为每个功率管设计了2个库所和10个变迁,因此,如果n表示输入变量的个数,那么,算法2的时间复杂性是12n,即算法2具有多项式级的时间复杂性.
3 基于可达图的分析和验证
在获得驱动电路的控制Petri网模型后,定义输入变迁和输出变迁的激发规则,生成的状态可达图可以完整地呈现程序运行过程中的状态迁移.
根据控制Petri网模型(图3),通过可达图算法,得到无刷直流电机的控制Petri网可达图,如图4所示.图4中:每个状态表示一个向量,即
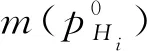

图4 直流无刷电机的控制Petri网可达图Fig.4 Reachable graph of BLDC motor control Petri nets
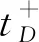

表2 可达图中关键结点表示的状态Tab.2 Status represented by key nodes in reachable graph
为了使可达图更加简洁明了,对其他结点(图4)进行隐藏.如实线有向弧所示,在电机正转(反转)过程中的状态切换时,隐藏了3个中间状态,例如,从状态m1到状态m3的切换过程中,隐藏了3个中间状态,这样的状态切换有12个,因此,电机正转或反转过程共隐藏了36个中间状态.如虚线有向弧所示,电机启动隐藏了3个中间状态,电机关断隐藏了2个中间状态,启动和关断各有12种可能,因此,电机启动和关断共隐藏了60个中间状态.如点划线有向弧所示,电机正、反转切换隐藏了40个中间状态,这样的切换共有12种可能,因此,电机正、反转切换共隐藏了480个中间状态.
在计算可达图时,涉及9个变量,包括3个霍尔传感器Hi、1个电机旋转方向控制变量D和6个功率管VTi.可达图状态随着变量个数快速增长,其状态结点数达到589个.
根据Petri网可达图,计算无刷直流电机动态系统的状态集合,并根据换向逻辑将信号逐个代入逻辑表达式,验证是否符合规范,若不符合,则重新设计系统的Petri网模型.
4 基于Petri网的电机驱动DSP逻辑控制程序的设计
根据无刷直流电机驱动电路的Petri网模型设计无刷直流电机的DSP逻辑控制程序.
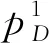
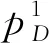

步骤4借助每个功率管的Petri网,根据每个变迁的执行逻辑,设计无刷直流电机DSP逻辑控制程序,编写功率管VTi的赋值程序指令.
以功率管VT3为例,其DSP控制程序为VT3=!VT3*(!H1*H2*H3D+!H1*H2!H3*D+H1*!H2*!H3!D+H1*!H2*H3!D)+VT3*!(!H1*!H2*H3+H1*H2*!H3+H1*!H2*!H3*D+H1*!H2*H3*D+!H1*H2*!H3*!D+!H1*H2*H3*!D).
在VT3的DSP控制程序中:当VT3为0时,表示管子开始由关断切换到导通,第一个括号中的布尔公式表示导通条件;当电机正转,D为1,霍尔信号H1H2H3为011和010时,VT3是导通的;当电机反转,D为0,霍尔信号H1H2H3为100和101时,VT3是导通的.
当VT3为1时,表示管子开始由导通切换到关断,第二个括号中的布尔公式表示关断条件;当电机正转时,D为1,当霍尔信号H1H2H3为100和101时,VT3是关断的;当电机反转,D为0,霍尔信号H1H2H3为010和011时,VT3是关断的;无论电机是正转还是反转,当霍尔信号H1H2H3为001和110时,VT3都是关断的.将控制程序与表1一一对应进行验证,可证明控制逻辑是正确的.
5 实验分析
无刷直流电机转速控制实验装置,如图5所示.无刷直流电机DSP控制实验系统采用TPR3003-3C型电源(广东省深圳市安泰信电子公司);无刷直流电机(江苏省南通市海安华洋机电有限公司)的额定电压为24 V,额定转速为1 600 r·min-1;F28335型开发板、BLDC-V2型驱动电路(江苏省南京研旭电气科技有限公司);ZDS2024PLUS型示波器(广东省广州致远电子股份有限公司);TPS2024B型示波器(上海市泰克科技(中国)有限公司).
将基于Petri网的无刷直流电机DSP逻辑控制程序下载到开发板,完成开环正、反转和速度环正、反转实验.供电电压为24 V,电机速度环正转转速为1 600 r·min-1,反转转速为-1 600 r·min-1.
电机正、反转实验中的速度变化曲线,如图6所示.图6中:v为电机转速.电机先正转,然后,再切换到反转,多次正、反转切换.
当电机正转和反转时,霍尔信号和功率管的电压(U)变化曲线,如图7所示.
图7中:PWM信号表示管子导通,高电平表示管子关断.当电机正转,霍尔信号为101时,管子VT1和VT6是导通的;当霍尔信号为001时,管子VT1和VT2是导通的;当霍尔信号为011时,管子VT2和VT3是导通的;当霍尔信号为010时,管子VT3和VT4是导通的;当霍尔信号为110时,管子VT4和VT5是导通的;当霍尔信号为100时,管子VT5和VT6是导通的.
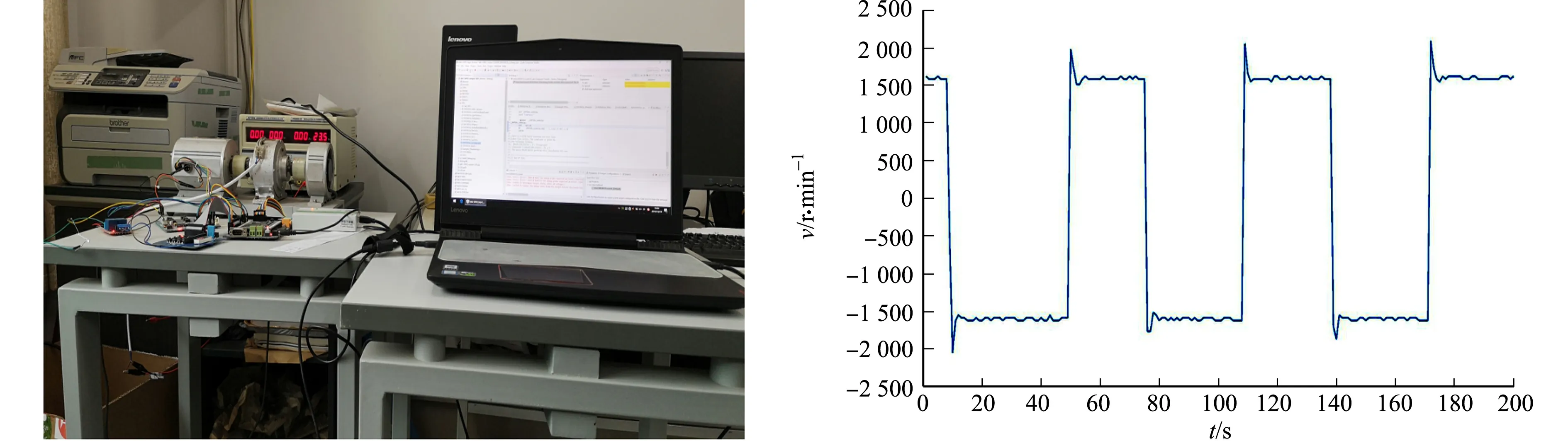
图5 无刷直流电机转速控制实验装置 图6 无刷直流电机正、反转实验中的速度变化曲线Fig.5 BLDC motor experiment device of speed control Fig.6 BLDC motor speed change curve in positive and negative rotation experiment
当电机反转,霍尔信号为101时,管子VT3和VT4是导通的;当霍尔信号为001时,管子VT4和VT5是导通的;当霍尔信号为011时,管子VT5和VT6是导通的;当霍尔信号为010时,管子VT1和VT6是导通的;当霍尔信号为110时,管子VT1和VT2是导通的;当霍尔信号为100时,管子VT2和VT3是导通的.实验结果与表1相符.
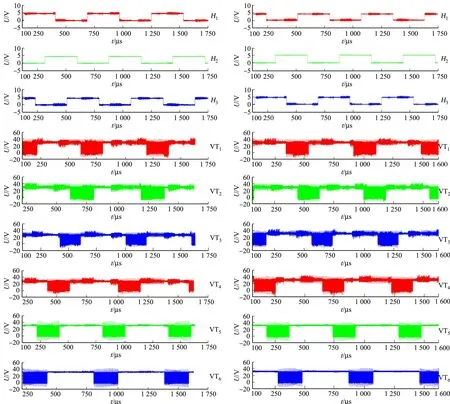
(a) 电机正转 (b) 电机反转图7 霍尔信号和功率管的电压变化曲线Fig.7 Change curves of Hall signals and MOSFET voltage
传统的无刷直流电机DSP逻辑控制程序的设计和调试比较繁琐,难以避免程序中的逻辑错误,而Petri网可克服现有技术的不足.首先,根据Petri网可达图,计算无刷直流电机动态系统的状态集合;然后,根据换向逻辑将信号逐个代入逻辑表达式,验证其是否符合规范,若不符合,则重新设计系统的Petri网模型.因此,通过Petri网先保证控制程序的逻辑正确性,再进行DSP程序的设计,无需反复测试.
6 结束语
设计无刷直流电机系统的控制Petri网模型,利用可达图验证模型表示的控制逻辑,根据Petri网设计DSP逻辑控制程序,并进行实验验证.
利用基本环状结构描述霍尔传感器和旋转方向控制变量,并按二二切换规则设计功率管库所状态切换变迁,获得无刷直流电机的控制Petri网模型;利用可达图算法对系统状态逐一验证,确保模型的正确性和可靠性;最后,给出Petri网转换为DSP程序的方法,并进行实验验证.相较于文献[9-10]的谓词Petri网,文中方法基于普通Petri网设计无刷直流电机的控制器,每个变量均描述为网络结点,具有更为严格的形式化语义,能够采用可达图算法进行严格的控制系统分析和验证.

