基于主体退出效应的灰色无标度网络优化模型研究
◆段林博 王迪飞
(1.中国电子科技集团公司第二十八研究所江苏 210007;2.南京航空航天大学经济与管理学院江苏 211106)
无标度网络演化模型(简称BA模型),是Barab演化模和Albert通过提取真实网络演化过程中普遍存在的规模增长与偏好选择两种机制建立的网络演化模型[1]。BA模型突破以往假定网络规模不变与网络结构始终为规则或均匀的限制,使得演化机制能够在更符合现实的情境中进行研究,极大地拓展了以网络为工具研究实际动态网络性质的应用范围。然而,BA模型只考虑了实际网络中的部分演化机制,主体退出行为、主体间连线断键等现象并未考虑。因此,BA模型的某些性质与真实网络仍有较大差异,普适性较弱。主体退出行为会在很多实际网络中出现并伴随网络的整个演化周期,例如市场中主体的退出是市场经济的一个必然要求,因为一个经济体没有退出,就不可能产生有效的市场定价机制,进而也就不可能形成资源的优化配置。战略性新兴产业集群、技术创新网络等亦是如此,没有主体的退出,就无法催生新循环,集群网络没有了新鲜血液,整体的效率就会降低,新兴技术停滞不前,错失发展良机。因此,利用BA模型研究主体退出效应更加贴合实际,更具实践意义。
目前,结合BA模型研究主体退出效应的文献数量相对较少,主要集中在理论推导和数值仿真两个方面。Moore C[2]构建了随机删除节点的网络演化模型,发现随着删除节点规模的不断增大,度指数发散,网络度分布从幂律分布逐渐向广延指数分布过渡,并通过模拟仿真验证了结论的有效性。Feng M[3]构建了反择优删除节点的网络演化模型,利用模拟仿真得出模型的度分布呈幂律形式。Shi D等[4]研究了优胜劣汰演化模型,利用平均场方法推导了模型度分布的近似解,演化网络服从度指数为(1,4]的无标度网络。Kong X等[5]构建了连边的一端择优选择,另一端在被选择节点的邻域中随机选取的连边删除网络演化模型,利用马尔可夫链理论求得该模型度分布的精确解,并得出新增连线在大于删除连边数量时,网络才具有无标度性,且度指数在(3,5]范围内。Li J等[6]研究了基于时齐泊松过程的“嵌入——删除——补偿”的网络演化模型,发现模型的度指数在(1,3]之间。
通过梳理上述文献,发现优化模型均认为每一时间步删除节点的行为是必然发生的,而现实中主体退出是具有某种不确定性的行为;节点的删除主要分为随机与反择优两种选取规则,反择优规则也包含不同的定义。若用某一概率值反映主体退出的不确定性,则固定概率值的演化模型仅对应一种可能性。因此,本文运用灰数表征主体退出的不确定性,并考虑三类不同的主体退出方式,结合BA模型,构建了基于主体退出效应的灰色无标度网络优化模型。本文以理论基础、模型构建和算例仿真三部分依次展开,分析主体退出行为将会给网络带来何种效应。
1 理论基础
根据复杂网络理论,网络异质程度和小世界性是区分网络结构最基本且最主要的两个方面,并且本文是在BA模型的基础上对主体退出效应进行研究。因此,理论基础部分按无标度网络演化算法、反映网络异质程度的网络度分布和网络小世界性的聚类系数三部分进行介绍。
1.1 无标度网络演化算法
(1)增长:给定一个含有m0个少量节点的初始网络,每一单位时间内生成一个带有m(m≤m0)条连边的新节点,每条连边选择一个已有节点进行连接,不允许重复连接和自连接。
(2)偏好连接:新节点与已有节点vi相连的概率Π(ki)由下式表示:

其中ki表示节点vi在时刻t拥有的连边数,即度数。分母表示网络在时刻t的总度数。从式(1)可以看出,已有节点的度数越大,其获得新节点连边的可能性也越大。随着网络的不断演化,这类节点获得新节点连边的能力越来越强,富者愈富的现象逐渐形成,从而复现了二八定律。
1.2 网络无标度特征
网络度分布是反映网络无标度性的主要指标。网络度分布的定义根据不同的推导方法会有不同的形式,但本质上完全相同。本文采用平均场方法,因此,基于平均场方法[7]的网络度分布定义如下:
定义 1[7]在时刻t从网络中随机选择一个节点,称节点自身拥有的连线数量为节点的度数。若该节点度数恰好为k的概率为P(k,t),则称P(k,t)为时刻t网络的瞬时度分布。当网络规模足够大时,若极限存在,则称P(k)为网络的稳态度分布。
BA模型的稳态度分布存在,根据平均场方法推导出的结果为P(k) = 2m2k-γ,其中γ=3为网络度分布的度指数。根据P(k)的幂函数形式,BA模型的度分布呈幂律性质,异质程度较高,该分布在双对数坐标系中近似为一条直线。研究表明,网络的异质程度随度指数γ取值的不断增大而逐渐降低,即网络愈来愈趋于同质化。
1.3 网络小世界特性
网络的小世界特性可由网络聚类系数反映。网络聚类系数的定义是通过节点聚类系数定义的,节点聚类系数的定义如下:
定义2[8]称与节点vi直接相连的节点为节点vi的邻居节点,节点vi的集群系数Ci定义为节点vi与ki个邻居节点之间实际存在的边数Ei与理论中总边数ki(ki-1)/2的比值。
因此,网络集群系数C就是所有节点集群系数的平均值,即
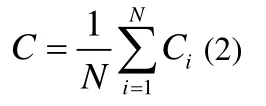
BA模型的聚类系数的建模较为复杂,可通过数值模拟的方法得到C=N-0.75,比同规模现实网络的集群系数要小很多。
根据文献[8],网络的聚类系数可表征主体间信息流动的稳定性与效率。聚类系数的增大说明某个主体与其他主体接触的数量变多、主体间相互交流更加频繁,网络稳定性越高,鲁棒性越强。
2 考虑主体退出效应的灰色无标度网络优化模型构建
根据文献[2-3,9],本文总结了三类节点退出方式。令N(t)表示时刻t网络的节点数量,ki(t)为时刻t节点vi的度数,简记为ki;Π(ki)为新节点的偏好连接概率。则主体可按随机Γ1、反择优概率Γ2(ki)和反择优概率Γ3(ki)三种方式退出。其中,Γ1、Γ2(ki)和Γ3(ki)的函数表达式分别为

由式(3)和式(4)可以看出,三种选取方式均满足归一性,即Σi= 1 ,i=1,2,3。
在主体决定以某种方式退出之前,主体退出行为本身是具有不确定性的,即在网络演化过程中的每一时间步内,主体并不总是必然退出的。主体的退出行为是主体决策的意愿,而现实情况中主体对于周围环境的认知往往有限,其意愿应在某一范围内变化,表现为某种不确定性,这种不确定性并不能以单一数值全面反映出来。根据灰色系统理论[10],灰数可以很好地描述这类不确定性,因此,本文用灰数⊗表示主体退出的不确定性。为研究方便,若以 0表示主体必然不退出,1表示主体必然退出,则⊗的取值范围为 ⊗ ∈[0,1],即主体退出意愿的最大考虑范围为[0,1],但此次的可能性究竟为区间中的哪一个值并不可知。
结合以上分析,构建基于主体退出效应的灰色无标度网络优化模型演化算法如下。
给定一个节点数量为m0的初始网络,此后的每一时间步有两个演化过程独立且同时发生:
Step1 产生a个新节点并进入原有网络,每个新节点以择优概率Π(ki)选择m个已有节点进行连接,不允许重复连接和自连接。
Step2 选择b个已有节点进行删除,被删节点与其连线一并移除原有网络。其中,被删节点可按式(3)中的三种形式进行选择,且决定该时间步删除原有节点的可能性为⊗。
由优化模型的演化算法可知,当a<⊗·b时,新节点产生的数量小于被删节点的数量,随着过程的演进,网络规模逐渐减小,直至为0。此种情况的网络一定是退化的。当a=⊗·b时,网络规模不变,在初始网络规模较小的情况下,此种情况的实际意义不明显。当a> ⊗·b,网络规模不断增大,这符合大多数实际网络的演化特征。
在所有关于网络度分布的研究方法中[8,10-14],均认为网络结构的变化与复杂系统类似,即网络规模较小时其结构并没有明显的规律。随着时间的推移,网络规模越来越大,其结构会呈现出明显的规律。基于此,首先将网络演化时间定格在较大的t值处。在a>⊗·b的条件下,主体无论选择何种方式退出,由于择优连接机制的存在,网络同质化的可能性很小。在异质化的前提下,网络中存在少数拥有大量连线的节点,其余节点的连线数很少。下面对两类反择优删除节点机制进行讨论。

则在反择优概率Γ2(ki)中,N(t)-1与 Σ ′均为较大的正整数,则(N(t) - 1 )-1≈N(t)-1。由于网络的异质性,1-Π(ki)的取值只有少数节点较小,大部分节点均较高,并且随着网络的不断演化,每一个ki对 Σ ′的贡献越来越小,则1 - Π(ki) = 1 -ki/Σ′≈1,且度数较大的节点在1-Π(ki)的取值也越来越大。因此,在时间t较大时,反择优概率 Γ2(ki)≈Γ1,即

在反择优概率Γ3(ki)中,网络中度数为0的节点相当于孤立节点,可认为已从网络中删除。因此 , Σ ′为调和级数,该级数发散。随着网络的演化,调和级数 Σ ′不断增大,在多数节点拥有少量连线的情况下,对于 Σ ′的贡献愈来愈趋于平均。因此,在时间t较大时,反择优概率 Γ3(ki)≈ Γ1,即

根据上述分析,在时间t较大时,两类反择优选择机制与随机选择非常接近。因此,本文以随机选取节点进行删除作为网络度分布的建模依据。由于网络聚类系数与平均路径长度在最简单的BA模型中建模已十分困难,至今没有很有效的方法进行解析研究。对于上述两种统计指标,本文会在第四部分给出其仿真结果。
在网络从t时刻至t+1时刻的演化过程中,主体vi度数的变化率由该单位时间内新主体的进入与原有主体的退出共同决定。令t时刻网络的连线总数为L(t),则新主体的进入使主体vi度数的增长率为
杨梅并没有被打晕,之所以装作被打晕,不与盗贼冲突,是爸爸教给她保全自己不再受二次受伤害的上上之策。就在杨梅佯装倒下后,她听见盗贼从工具包里窸窸窣窣翻东西的声音。还没等杨梅反应过来,嘴巴就被胶带封住了。杨梅立即睁开眼瞪着盗贼,盗贼一看晕倒的杨梅突然睁开眼睛也有点懵。但这个操着东北口音的盗贼连忙说:“我就跟你爸谈点事。你合作点,我就不伤害你。”

同时,原有主体的退出导致主体vi度数的下降率为

因此,根据平均场方法,可得如下主体vi度数的灰色动力学方程

由于主体以随机的方式退出,因此每一单位时间内网络连线的删除数量为原有连线均值的b倍,则优化模型中连边数量的变化规律由如下灰色微分方程表示:

结上以上分析,优化模型网络度分布由式(10)与(11)同时确定:
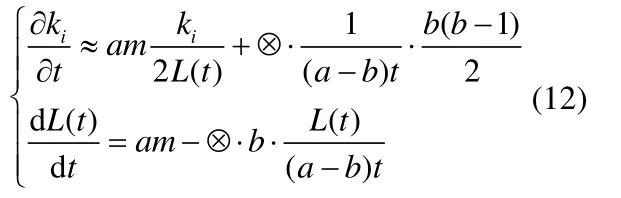
由于式(11)中参数L(t)嵌套在式(10)中,当计算出L(t)的解析表达式代入至式(10)后,求解式(10)的解析表达式较为困难,因此本文在第四部分采用数值解法与仿真结果进行对比。
4 算例仿真
本文以德国激光产业[15]作为案例背景,文中创新网络是以项目为纽带构建的。从激光产业1991年至2007年近16年的演化过程来看,每年都有新的主体加入,也有很多合作关系以及节点的消失,自身拥有合作数量较多的主体之间往往也存在联系,在拓扑结构图中呈现很明显的密集区。从实证的统计结果可知,网络中主体的合作数量大多在[1,3]之间,少数主体合作数量可达46个。
首先,固定优化模型中所有的参数值。由德国激光产业的实际数据可知,创新网络的规模不断增大,显然有a>⊗·b,由⊗的范围可知,只要a>b即可。本文使用等权均值白化的方法白化灰数。因此,模型中所有参数的取值如表1所示。

表1 优化模型参数取值表
图 1展示了主体的不同退出方式所对应的演化网络的度分布情况。

图1 三类主体退出方式相应的网络度分布
由图1可以看出,主体以随机方式Γ1、反择优选取方式Γ2(ki)和反择优选取方式Γ3(ki)在网络演化时间较长时,三者的度分布近乎一致,这证明了第三部分对于两种反择优删除机制与随机删除机制几乎相同讨论的正确性;随机方式Γ1与反择优Γ2(ki)在小度数范围内的分布规律非常相似,而反择优选取Γ3(ki)在小度数范围内的分布规律与随机Γ1及反择优Γ2(ki)有较为明显的差异,前者在主体度数最小及次小处所占比例明显低于后两者,这说明度数逆的反择优选取方式更能降低度数最小和次小的比例。网络整体服从幂律分布,与BA模型不同的是,度数最小的节点数量所占节点总量的比重已不再最大,并且在最小度数与某个较小度数之间的对应度数节点的比例呈比例增加。因此,优化模型中在小度数范围内节点数量的分布规律与度数较大时完全相反。网络聚类系数随时间的演化规律如图2所示。
图2中三角形、菱形和五角形分别代表聚类系数按随机方式 Γ1、反择优选取方式 Γ2(ki)和反择优选取方式 Γ3(ki)演化的取值。从图中可以看出,聚类系数取值的下降速率按反择优选取方式 Γ3(ki)、反择优选取方式 Γ2(ki)和随机方式 Γ1依次增大,说明主体随机退出使网络的小世界性变得最差,因为随机方式会导致一些度数较大的主体以同样可能性被选取,这些主体退出后,网络的连通性变弱,小世界性变差。

图2 网络聚类系数变化规律图
下面考察网络统计指标对于主体退出不确定性的变化情况。注意到⊗为连续灰数,网络度分布、网络聚类系数均为一条窄带,因此下图只描绘当⊗取0、1/2、1时的图例,其余取值均在0与1之间变化。

图3 优化模型网络度分布随主体退出不确定⊗的变化规律图
由图 3可以看出,主体退出行为的不确定性对于较小度数节点的分布规律影响显著,而在度数较大节点的处的作用不很明显。随着灰数的白化值逐渐变大,小度数节点所占比例愈来愈大,说明网络的异质程度不断降低。
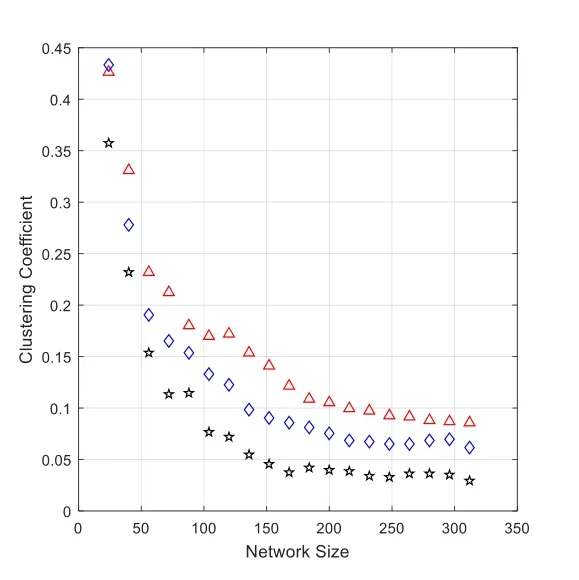
图4 优化模型网络聚类系数随主体退出不确定⊗的变化规律图
图4中三角形、菱形和五角形分别代表聚类系数按随机方式Γ1、反择优选取方式Γ2(ki)和反择优选取方式Γ3(ki)演化的取值。从图中可以看出,聚类系数随灰数白化值的增大而减小,说明主体退出的可能性越大,网络的小世界性越差。
5 结束语
本文尝试将区间灰数与经典无标度网络模型结合,研究主体退出的效应问题。主要得出以下两个结论:
(1)主体退出的方式对网络度数较大范围内节点分布规律的影响较弱,在度数较小范围内对节点分布情况作用明显。反择优方式Γ3(ki)在小度数节点处作用最强;网络聚类系数对主体退出的方式较依赖,随机方式Γ1的小世界性最差,反择优方式Γ3(ki)的小世界性最强。
(2)主体退出行为的不确定性对网络度数较大范围内节点分布规律的影响较弱,对度数较小处的节点分布作用明显,且随着可能性的增强,网络的异质性减弱;网络聚类系数与主体退出行为的可能性大小呈负相关关系,随着可能性的增强,网络的小世界性变差。
灰数的引进使优化模型网络的度分布、网络集群系数具备了一定的灰性,囊括了多种情形,而这些情形在实际中均有可能出现。因此,灰数拓展了无标度网络的应用范围。运用灰色无标度网络研究相关演化机理是今后研究的重点。

