Adaptive leader–follower formation control for swarms of unmanned aerial vehicles with motion constraints and unknown disturbances

Yueqian LIANG, Qi DONG, Yanjie ZHAO

China Academy of Electronics and Information Technology, Beijing 100041, China

KEYWORDS

Abstract In this paper, the 3D leader–follower formation control problem, which focuses on swarms of fixed-wing Unmanned Aerial Vehicles(UAVs)with motion constraints and disturbances,has been investigated.Original formation errors of the follower UAVs have been transformed into the Frenet-Serret frame.Formation control laws satisfying five motion constraints(i.e.,linear velocity, linear acceleration, heading rate, climb rate and climb angle) have been designed. The convergence of the control laws has been discussed via the Lyapunov stability tool.In addition,to address the unknown disturbances, an adaptive disturbance observer is exploited. Furthermore, formation control laws involving estimated disturbances are presented as well. The collision avoidance between UAVs is achieved with the artificial potential method. Simulation results obtained using four scenarios verify the effectiveness of the proposed method in situations with constant disturbances and varying disturbances, as well as without disturbances.

1. Introduction

Recently,the swarm concept has attracted increasing attention around the world and has been defined as a game-changing technology.1In October 2016, 103 Perdix Unmanned Aerial Vehicles (UAVs), also called drones, were dropped from three F/A-18 Super Hornet fighter jets in a joint effort with the US Naval Air Systems Command over their base at China Lake,California.2Then in 2017, China launched a record-breaking swarm of 119 fixed-wing unmanned aerial vehicles.3In May 2018,a Chinese company Yunzhou-Tech unveiled its test video of a swarm of 56 unmanned boats.4Besides, performances using hundreds and thousands of robots or UAVs have become pervasive worldwide.

The essential reason for the rising of the swarm, typically the UAV swarm,is that compared to a single UAV,when multiple UAVs are well coordinated,there are many advantages in mission efficiency, low energy consumption, robustness, faulttolerance,flexibility,and so on.UAV swarm is becoming a disruptive technology to enable highly reconfigurable, ondemand,distributed intelligent autonomous systems with high application potentials to many areas of science, technology,and society.5The formation control technology is one of the essential ones to guarantee successful mission execution when using UAV swarms.

Formation control can generally be classified into two categories: one is the exact formation control,6and the other is the flocking control.7The former requires the swarm to maintain a predefined geometrical configuration, while the latter makes the swarm form an amorphous formation generally by simple rules such as alignment, cohesion, separation,etc.8–12Herein the former type of formation control is investigated.In Ref.6,based on the sensing capability and the interaction topology, Oh et al. categorized the formation control methods into three types, which are position-based,displacement-based, and distance-based formation control methods. The position-based formation control method requires the most advanced sensing capability, whereas the least interactions, which is the opposite situation for the distance-based formation control method.

According to fundamental ideas in control schemes,formation control methods can usually be classified into the leader–follower method,13,14the virtual structure method,15,16the behavior control method,17,18the artificial potential method,19,20the consensus-based method,21–29etc.As the most classical method,the leader–follower method specifies the hierarchy of the formation control problem and generally needs the least communication connects between the UAVs.The virtual structure method treats the formation as a rigid structure,requires no leader and has high formation accuracy. The behavior control method achieves the formation control by using some simple behavior modes predefined for the UAVs.However, the convergence cannot be strictly proved mathematically. The artificial potential method originates from the potential method for collision avoidance in the robot field,and its usage difficulty lies in the designing of appropriate potential functions for different application scenarios. The consensus-based method has been paid more and more attention these years because it is easy to implement and is a distributed method. Some further discussions about these formation control methods and other methods can be found in Refs. 5,30,31, and also the literature listed therein.

Though extensive results have been achieved for the formation control problem, the researches considering the practical motion constraints of the UAVs especially the fixed-wing UAVs are still not enough and thorough.Ren32and Abdessameud and Tayebi33utilized the tanh function to design bounded inputs for second-order multiagent systems. Li et al.used the saturation function to propose finite-time consensus control for linear time-invariant multi-agent systems.34Some considered the input saturations as vector constraints,35–37but this is not the case in practical applications.Zhao et al.proposed a general approach for coordinated control of multiple agents and addressed the motion constraints using the saturation function38. Yu and Liu investigated the planar formation control of the nonholonomic vehicles subject to linear velocity and angular velocity constraints.39However, only the twodimensional situation was considered and complete constraints were not solved by them.

Motivated by the above discussions, in this paper we further study the formation control problem of fixed-wing UAV swarms with both motion constraints and unknown disturbances. The main contribution of the paper is as below: Five types of motion constraints, which are linear velocity constraint, linear acceleration constraint, heading rate constraint,climb rate constraint and climb angle constraint, are considered,and furthermore,in the framework of the leader–follower method, nonlinear formation controllers satisfying these constraints are proposed by using the rotating formation errors and the saturation function.

The remainder of the paper is organized as follows. In the next section, the detailed problem is formulated. In Section 3,the formation controllers without and with unknown disturbances are designed to meet the motion constraints. Then in Section 4,four simulation scenarios are given to assess the proposed method. In the last section, a short conclusion is provided.

2. Problem formulation

2.1. UAV model and motion constraints

Fig.1 Communication structure.

Fig.3 Formation errors in Scenario 1.

The formation control laws given in Eqs.(45),(26)and(46)now always satisfy the mentioned motion constraints given in inequalities (2)-(6).

Remark 3. The main role of the introduction of the saturation function is to impose restrictions on the control and state variables during the initial phase. After that, the formation errors of the followers with respect to the leader can usually be reduced significantly, which further reduces the magnitudes of the original (before the usage of the saturation function)control and state variables to the extent that they are between the lower saturation bound and the upper saturation bound.This means that the saturation function does not work after some initial phase.These conclusions can be partially observed from the simulation discussions in Section 4. However, the theoretical results about the influence of the introduction of the saturation function on the stability of the closed-loop system are still to be explored.

3.3. Formation controller with disturbance

Under the situation that the unknown disturbances exist for the UAV swarm, the disturbances are firstly estimated by the above-designed observer. Then the formation control laws given in Eqs. (25)-(27) should change to

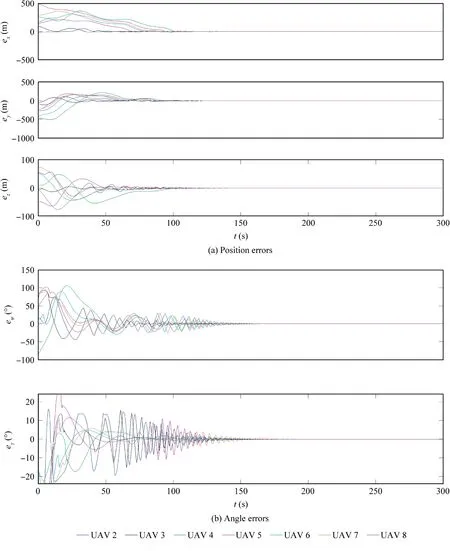
Fig.7 Formation errors in Scenario 2.

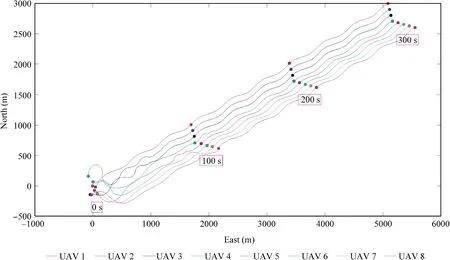
Fig.8 Flight trajectories of UAV swarm in Scenario 2.

Fig.9 Control inputs in Scenario 2.

In order to satisfy the linear acceleration constraint given in inequality (3) and the climb angle constraint given in inequality(6),similarly as before,Eqs.(47)and(49)are then adjusted to

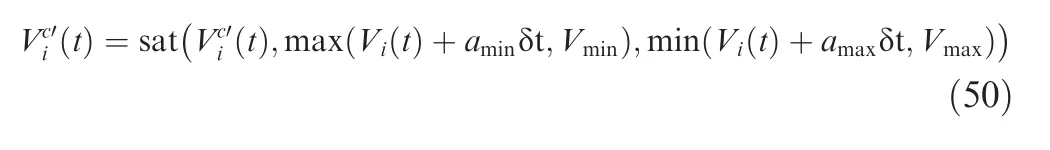
and

respectively.

3.4. Collision avoidance consideration

The artificial potential method is adopted herein to address the possible collisions between the UAVs. Choose Zras the collision avoidance distance, i.e., when the distance between two UAVs is less than Zr, the related UAVs should take some collision avoidance strategy which is determined by the designed artificial potential.Herein, for the i-th UAV, we choose its artificial potential as20

Fig.10 Acceleration, heading angle and climb angle in Scenario 2.

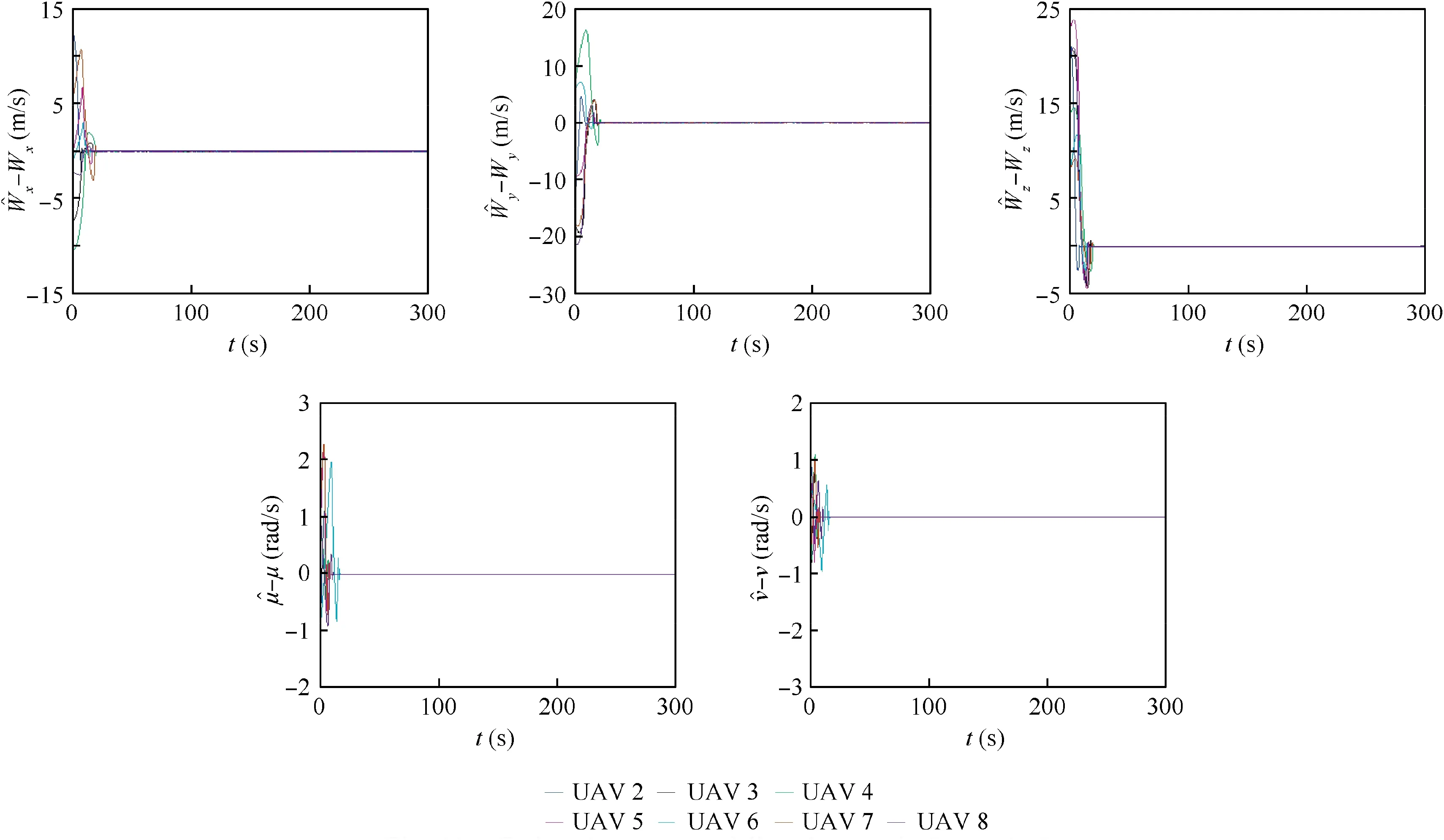
Fig.11 Estimation errors of disturbances in Scenario 2.

where

When it is necessary, the negative gradient of the artificial potential, which is－∂Ui/∂pi, is employed to generate feasible control laws for the linear velocity, the heading rate and the climb rate to achieve the collision avoidance. In specific, the collision avoidance control laws are given as

Fig.12 Formation errors in Scenario 3.

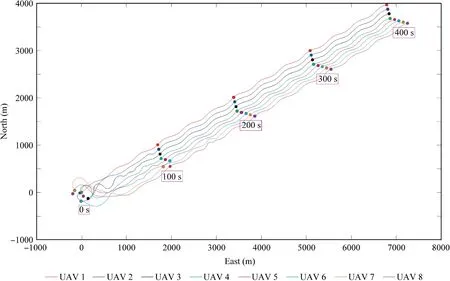
Fig.13 Flight trajectories of UAV swarm in Scenario 3.

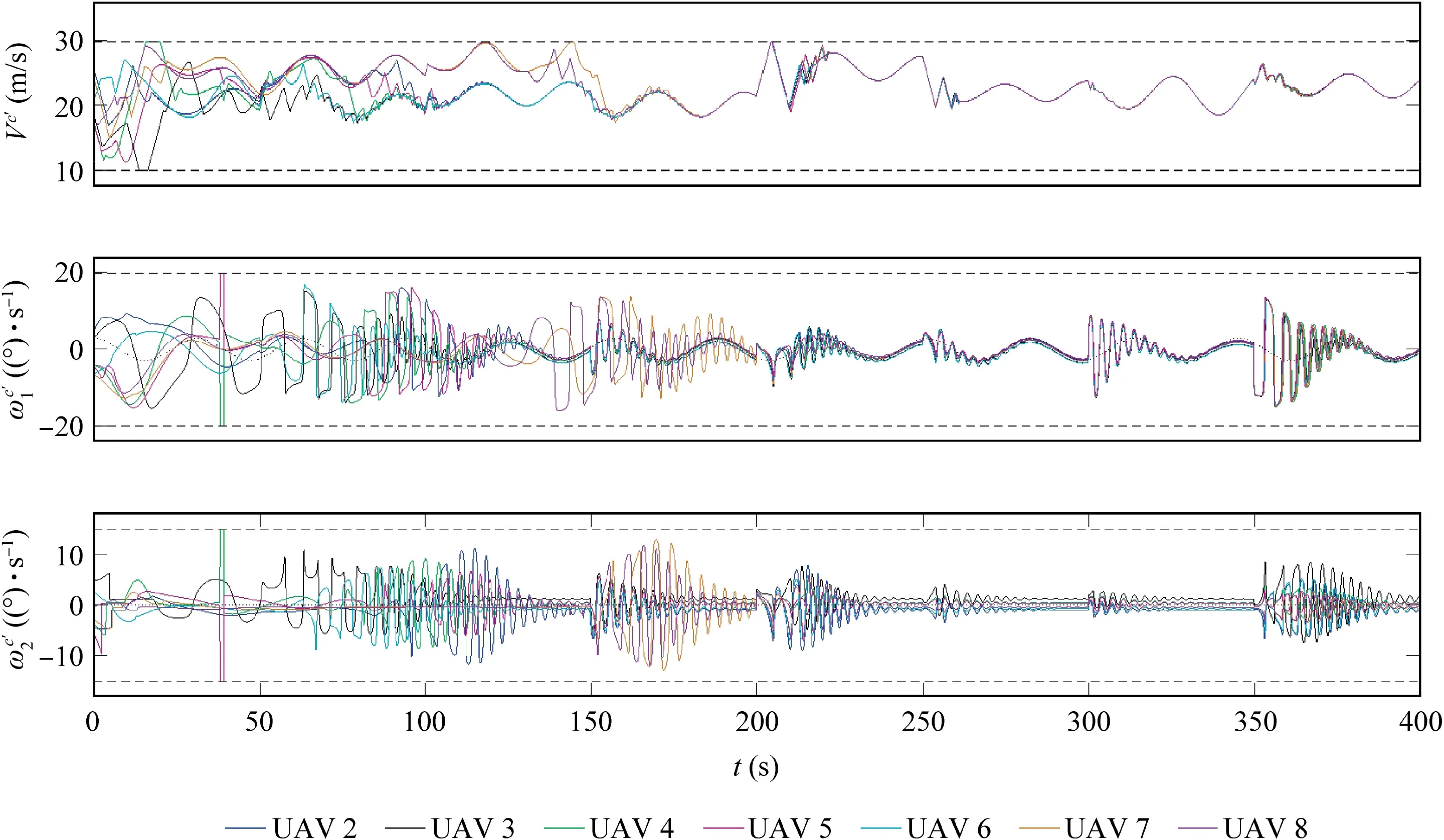
Fig.14 Control inputs in Scenario 3.

4. Simulation verification

4.1. Simulation settings

In this section, four simulation scenarios are conducted to assess the proposed adaptive formation control strategy. In the first three scenarios, the energy-saving V-shape is chosen for the UAV swarm comprised of 8 fixed-wing UAVs. And in the fourth scenario, the UAV swarm is assumed to include 24 fixed-wing UAVs and is used to mimic a large flying-wing aircraft shown below.

The desired distance between each two neighbor UAVs is set to be 100 m, from which the desired relative positions of the follower UAVs with respect to the leader UAV can be obtained. The collision avoidance distance is chosen as Zr＝20 m. The positive constants in the adaptive gains are chosen as follows: ϖil＝1, γil＝1, εi1＝1with l ＝1，2,σT，i1＝0.004 and σT，i2＝0.0002. The positive constants in the formation controllers are selected as k0＝0.011, k1＝6,k2＝0.611 and k3＝0.458. We set the small positive constant κ in Eq. (46) as 0.001.

The motion constraints of the follower UAVs and those of the leader UAV are listed in Table 1 and Table 2 respectively.

Fig.15 Estimation of disturbances in Scenario 3.

Fig.16 Sketch of a flying-wing aircraft.

4.2. Simulation results

4.2.1. Scenario 1: V-shape, no disturbance

Fig.17 Flight trajectories of UAV swarm in Scenario 4.

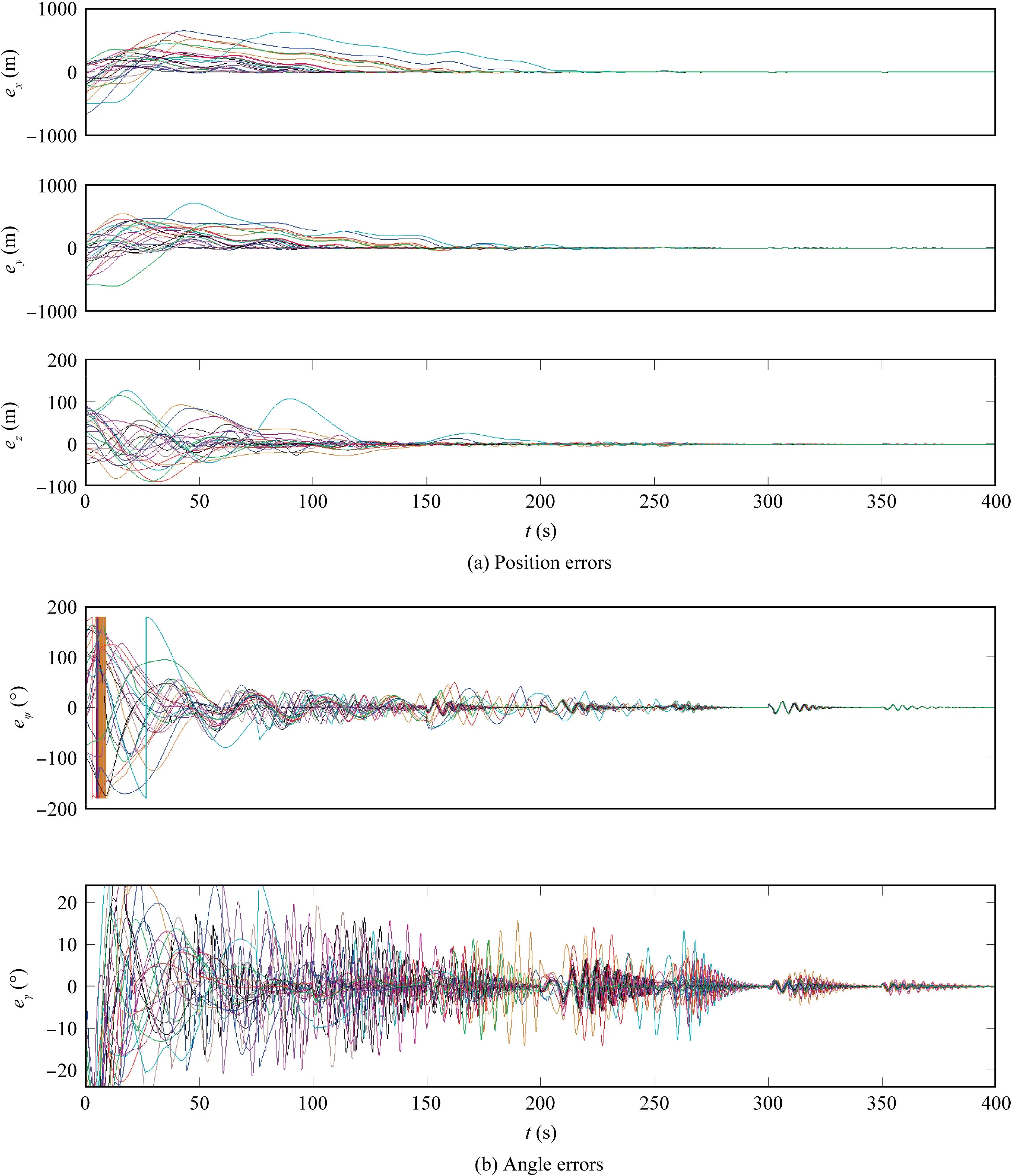
Fig.18 Formation errors in Scenario 4.

In Scenario 1,suppose there is no disturbance, and the swarm consisting of 8 UAVs is controlled to form a V-shape.The simulation results are shown in Figs. 2–6. Fig.2 depicts the flight trajectories of the 8 UAVs from the top view. Figs. 3 and 4 show us the evolution of the formation errors and the rotating formation errors with respect to the time, from which we can find that all the errors converge to 0 at about 200 s.This means that the V-shape formation has been formed at about 200 s,and the swarm will move forward with the leader UAV and in the meantime maintain this formation afterwards.Note that the rotating heading angle error and the rotating climb angle error are the same with the heading angle error and the climb angle error respectively. From Fig.5, we can easily find that after about 200 s, the control inputs (the linear velocity, the heading rate and the climb rate given by Eqs. (45), (26) and(46)) of the follower UAVs become the same with each other.Moreover, the magnitudes of these control inputs satisfy the constraints given in inequalities(2),(4)and(5).And similarly,it can be found from Fig.6 that the acceleration, the heading angle and the climb angle of all the follower UAVs coincide with each other and satisfy the constraints defined in inequalities (3) and (6) as well.

4.2.2. Scenario 2: V-shape, constant wind

In Scenario 2, the disturbance is set to be constant with W t（ ）＝3，5，0.5［］Tm/s. The constant values of both of μit（ ）and νi（t ） are randomly chosen from the normal distribution N（ 0，0.012）,which is the same selection method in the remaining two scenarios. The formation errors are illustrated in Fig.7, from which it can be seen that all of the errors are almost zero from about 200 s, implying the achievement of the V-shape formation. The flight trajectories of the UAVs are given in Fig.8. The control inputs obtained by Eqs. (50),(48) and (51), and the acceleration, the heading angle and the climb angle are depicted in Fig.9 and Fig.10 respectively.Because the acceleration is not straightly controlled and no chattering reducing approach is exploited, the acceleration experiences severe fluctuations. The estimation errors of the disturbances are shown in Fig.11,from which we can observe that the errors quickly reduce to about zero after some initial effort.

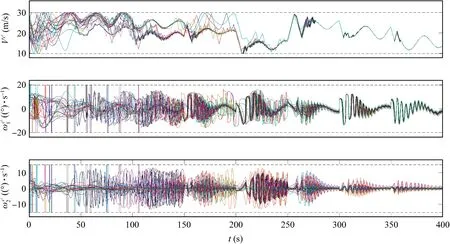
Fig.19 Control inputs in Scenario 4.

4.2.3. Scenario 3: V-shape, gust wind

In this scenario,the wind disturbance is set to be gust winds.In specific, the wind is assumed to change in every 50 s, and the magnitudes of Wxt（ ）, Wyt（ ） and Wzt（ ） are chosen randomly from the normal distributions N 0，32（）, N 0，52（）and N（ 0，0.52）respectively. The evolution of the formation errors can be found in Fig.12. We can observe that when the wind changes, the errors (especially those of the angles) will enlarge suddenly, but they (especially those of the position components) will reduce to zero quickly. This means that the formation configuration can be kept well though in the presence of gust winds.Fig.13 depicts the corresponding flight trajectories of the UAVs.In Fig.14,the control inputs are depicted,from which one can easily find the influence of the gust winds. The estimation results of the disturbances can be found in Fig.15.One can see that the change of the wind can be well captured by the designed adaptive observer.

4.2.4. Scenario 4: Flying-wing-shape, gust wind.

In Scenario 4, a swarm consisting of 24 UAVs is used to simulate a flying-wing aircraft sketched in Fig.16. The wind situation is the same as in Scenario 3.The flight trajectories of the UAVs are shown in Fig.17, from which we can observe the approximate flying-wing shape from about 300 s. From Fig.18,we can see the evolution of the formation errors versus the time. Similarly as in Scenario 3, we can see that unlike the flight angle errors, the position errors only experience small fluctuation at the moment of wind change. The control inputs are illustrated in Fig.19.

5. Conclusions

We have investigated the 3D formation control of fixed-wing UAV swarms including five kinds of motion constraints and unknown disturbances. The motion constraints have been explicitly addressed by introducing the rotating formation errors in the Frenet-Serret frame and the saturation function.The disturbances have been adaptively estimated by employing a finite-time disturbance observer.The effectiveness of the proposed method has been verified by four simulation scenarios.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China (Nos.61803353 and U19B2029) and the China Postdoctoral Science Foundation (No. 2017M620858).