Two-phase guidance law for impact time control under physical constraints
Yng TANG, Xioping ZHU, Zhou ZHOU, Fei YAN
a National Key Laboratory of Science and Technology on UAV, Northwestern Polytechnical University, Xi’an 710065, China
b UAV Research Institute, Northwestern Polytechnical University, Xi’an 710065, China
c School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
KEYWORDS
Abstract An impact-time-control guidance law is required for the simultaneous attack of suicide attack unmanned aerial vehicles. Based on the nonlinear model, a two-phase guidance strategy is proposed. The impact time is derived in a simple analytical form of initial states and switching states,and it can be controlled by switching at an appropriate range.Firstly,a two-phase guidance law is designed to make the magnitude of the heading error decrease monotonically from its initial value to zero.And then,the feasible interval of the switching ranges and of the impact times under the acceleration constraint are given analytically in sequence.Furthermore, a general form of twophase guidance law is proposed,which allows the magnitude of the heading error to increase in the first phase, to improve the applicability of the methodology. Having the same structure as proportional navigation guidance with a time-varying gain,the proposed algorithms are simple and easy to implement.The corresponding feedback form is presented for realistic implementation.When a predefined impact time is taken within its permissible set,the constraints on the acceleration and fieldof-view will not be violated during the interception.Finally,simulations validate the effectiveness of the methodology in impact time control and salvo attack.
1. Introduction
As a kind of precision-guided munitions, the suicide attack Unmanned Aerial Vehicle (UAV) is fast becoming a research hotspot of the military powers due to some advantages over the conventional missile. With the rapid development of antimissile technology, it is found increasingly difficult for the UAV to penetrate the powerful defense systems equipped by high-value targets, such as ground radars or warships. A simultaneous attack against a common target by multiple suicide attack UAVs can make the defense systems be saturated,and unable to conduct timely interference and interception,greatly enhancing the survivability of the UAVs. The control of impact time is the key to the simultaneous arrival of multiple UAVs.
A simultaneous attack can be achieved in two ways.One is individual homing, in which a common impact time is appropriately determined and loaded to the interceptor in advance,after that each interceptor completes the attack mission independently by applying Impact-Time-Control Guidance(ITCG).The other is cooperative guidance based on a communication network, where all members rely on online data links to synchronize the impact times,1thereby reducing the reliability of the weapon system. In this paper, the problem of ITCG is investigated.
Since an ITCG law was first introduced for anti-ship missiles,such subjects have been attracting much interest in recent years. The guidance law in Ref. 2 achieved time control by combining proportional navigation guidance with an additional feedback term of the impact time error. In Ref. 3, a polynomial guidance command was derived, and its coefficients were determined by boundary conditions and constraints on impact time and angle. These two algorithms are simple in form and easy to implement, but they rely on linearization in derivation under small angle assumption, which limits their applicability.Based on the accurate time-to-go calculated in nonlinear framework4,5or the estimated one obtained by approximation methods6–10, nonlinear control methods have been used to eliminate the impact time error and increase the robustness. However, these algorithms are usually complex, and it is difficult to analyze the influence of different parameters. Besides, the acceleration required at the initial time of guidance could be tremendous, and there may be singularity sometimes.
In order to adjust the impact time,ITCG laws usually make the interceptor’s trajectory very curved, sometimes leading to the seeker’s failure of maintaining a lock on the target or saturated acceleration. To confine the look angle to the seeker’s Field-of-View (FOV), in Ref. 11 a switching logic was proposed. When the look angle approaches the boundary of the FOV, the ITCG law will be switched to another algorithm to make the look angle no longer increase. In Ref. 12, a rule of the cosine of weighted look angle in the bias term was used to achieve this purpose. In Ref. 13, a backstepping-based ITCG law was proposed. The look angle is taken as a virtual control input, and its magnitude is limited by the controller gain.The guidance laws designed in Refs.14–16 made the look angle monotonically change from the initial value to zero to guarantee that the FOV constraint was not violated.However,all the work mentioned above did not deal with the acceleration limit of the interceptor. In Ref. 17, an ITCG law was designed to track a look angle profile, which is polynomial in time. Therein, the extreme values of acceleration and look angle are given analytically in the form of the guidance gain,which is determined by numerically solving an integral equation to meet the time constraint. Therefore, unexpected situations can be prevented by appropriately setting the impact time before guidance. However, a guide to the suitable choice of impact time is hard to obtain. Moreover, this kind of openloop control based on off-line calculation is often affected by disturbances, which tends to cause error accumulation.
Based on the above discussion, a two-phase ITCG strategy is proposed for the realization of the salvo attack in this paper.A Two-Phase Guidance (TPG) algorithm is first derived to reduce the magnitude of the heading error monotonically,and successively a Generalized Two-Phase Guidance (GTPG)law is proposed.Directly dealing with the nonlinear equations,this strategy uses the idea borrowed from Ref.14 to design the guidance laws without any approximation or linearization process. On this basis, Ref. 14 is improved in the following aspects:
(1) A two-phase guidance strategy is proposed, in which a switching mechanism is introduced to control the impact time. A simple function is used to relate the heading error variation to the range in each phase, resulting in a simpler guidance law. Taking the switching range as the single parameter for time control, which can be calculated analytically, the switching logic is concise.
(2) It is no longer required that the magnitude of the heading error decreases to zero strictly in time during the engagement. In TPG, it is designed to monotonically decrease to zero, while in GTPG, it is even allowed to increase in the first phase, further expanding the scope of application of the two-phase guidance strategy.
(3) Considering the acceleration limit and the FOV constraint,the permissible set of impact times can be calculated.In TPG,it is given analytically according to initial conditions and the acceleration limit.While in GTPG,it is obtained by solving two optimization problems related to initial conditions and constraint boundaries of the FOV and acceleration.
The remainder of this paper is organized as follows: The ITCG problem is described in Section 2. And then, TPG and GTPG algorithms are derived and analyzed in detail in Section 3. Simulations are carried out in Section 4 to validate the effectiveness of the proposed methodology. Section 5 presents concluding remarks.
2. Problem statement
Consider a planar engagement geometry between a suicide attack UAV and a stationary target, which are represented by P and T in Fig.1, respectively. It is assumed that the UAV is moving with a constant speed v and maneuvers by applying a lateral acceleration a normal to its velocity. Here,the range-to-target is denoted by r, and λ,γ refer to the Lineof-Sight (LOS) angle and the heading angle, respectively.The initial and terminal states of the system are denoted by subscripts 0 and f respectively.
The governing equations can be described as:


Fig.1 Planar engagement geometry.

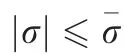
According to the definition of heading error, there is
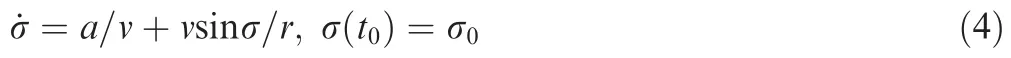


which satisfy the boundary conditions

respectively.
According to the previous discussion, both rfand ηfare taken as 0. The objective of this paper is to design a guidance command a to make tfconverge to the predefined impact time tdwithout violating the acceleration limit and FOV constraint.
3. Guidance law design
For the sake of time control, a simple idea is to calculate the total engagement time and control it with a single parameter.It is assumed that there are two instantsta,tb∈t0,tf[]in the guidance process satisfying ta<tb. The states corresponding to the instants are distinguished by subscripts a and b, respectively. From Eq. (5), we get

In order to perform the integral operation in Eq. (9), we need to relate the heading error variation to the range. For convenience, it is desirable that r is a strictly monotone function of η. We define the set of all the continuous functions r η( ) satisfying the boundary conditions r ηa( )=ra,r ηb( )=rbas Ξ,in which its subset Ξ′is defined as the set of all the strictly monotone functions in the interval η||<1. When r η( )∈Ξ′,Eq. (9) can be rewritten as
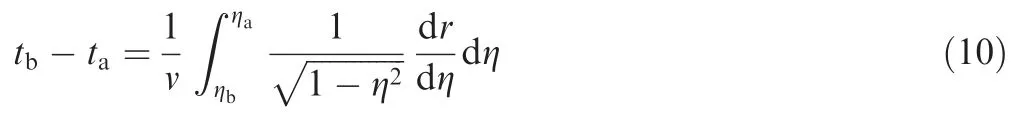
In general,to obtain a solution that satisfies n equality constraints, including two boundary conditions, we can assume
that r has the form of a weighted sum of n independent basis functions of η.

where the coefficients pi(i =0,1,...,n-1) are calculated to satisfy n equality constraints. If r η( )∈Ξ′, the candidate function is admissible.
Obviously, the expression of the duration is dependent on the choice of the reference profile r η( ). A common choice of the basis function is fiη( )=ηi. Only considering the case r η( )∈Ξ, it is advisable to choose

for simplicity.
(1) If ηa≠ηb, there is r η( )∈Ξ′. The coefficients are determined as

When r decreases from rato rb, the flight time can be acquired from Eq. (10).

From Eq. (6), the control command is derived as

(A) If rb≠0, there is

when t ∈[ta,tb]. The corresponding acceleration is

For analysis of the guidance law, the derivative of a with respect to η can be obtained after substituting Eq. (12) into Eq. (16)



where







Table 5 Permissible sets of the impact times.

Remark. When designing ITCG laws with FOV constraint,the velocity direction of the interceptor is generally considered to be the direction of its longitudinal axis because the coupling of guidance and control is neglected so that the aerodynamic angle is assumed to be small enough to be neglected. In practice,this is unacceptable sometimes.When considering the aerodynamic angle, we discuss this problem in the vertical plane. The look angle ε is defined as the angle between the interceptor longitudinal axis and the LOS. It can be expressed the sum of the heading error σ and the angle-of-attack α.

according to which we get




4. Numerical simulation
In this section, simulations are carried to verify the performance of the proposed strategy through various scenarios. It is assumed that the same type of suicide attack UAV is used in all scenarios with a constant speed of 170 m/s. The heading error limit determined by seeker’s FOV constraint is±50°,and its available lateral acceleration is 6g,where g =9.8 m/s2.The numerical integration is performed by the Runge-Kutta method with a fixed step of 0.01 s. All simulations are terminated when ˙r >0 or r ≤1.7 m.
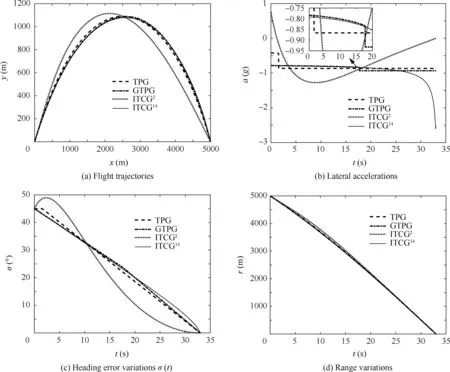
Fig.2 Results under different guidance laws.
The guidance laws in Ref.2 and Ref.14(denoted as ITCG2and ITCG14respectively)are considered as comparisons.With the help of the fmincon function provided in MATLAB, the interior-point method is employed to solve the constrained optimization problems in GTPG. Different initial guesses may lead to different optimal solutions. In GTPG, the initial guess of the switching states is taken as
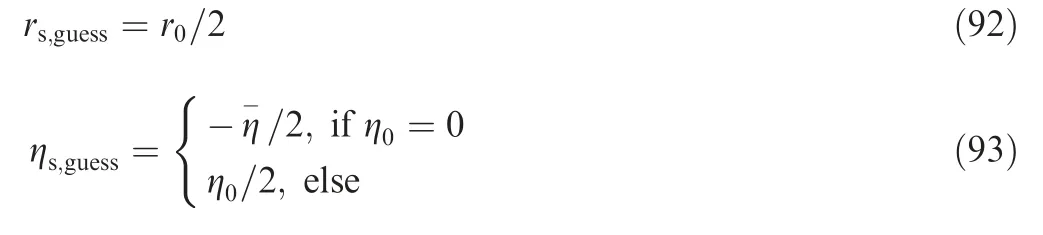
4.1. Impact time control for a single UAV
Consider a sample scenario with r0=5000 m and σ0=45°.An inertial coordinate system is established with the initial position of the UAV as the origin and the initial LOS direction as the x axis.
4.1.1. Comparison of the permissible sets of impact times under constraints
This section compares the impact-time-control capabilities of four ITCG laws under the same conditions. For a horizontal comparison,the case with σ0=-10°, r0=5000 m is also considered here. The permissible sets of impact times for individual laws are presented in Table 5, wherein the interval of the achievable impact times is obtained analytically in TPG or by the optimization algorithm in GTPG. While the laws in Ref.2 and Ref.14 cannot give the intervals in advance,which are obtained from numerical simulations and indicated by the superscript *.
When determining the permissible set of impact times for ITCG2and ITCG14, it is found that in general, the maximum of the achievable impact time tf,maxis determined by the FOV constraint, while the minimum, tf,min, is determined by the acceleration constraint.It makes intuitive sense that the larger the velocity is allowed to deviate from the LOS, the more curved the trajectory is, resulting in a longer duration of the flight. So a larger σ-leads to a larger tf,max. For the shortest time, the UAV must fly along the shortest trajectory: First,the heading error is brought to zero as soon as possible, and after that, the UAV flies along a straight-line trajectory until impact. Therefore, a larger a- results in a smaller tf,min.
First, a vertical comparison is performed for Table 5. As seen, TPG expanded the achievable impact time coverage in ITCG14by relaxing the requirement,that is strictly decreasing the magnitude of the heading error to zero until impact.Allowing the magnitude of the heading error to increase in the first phase,GTPG can capture the target along a less direct trajectory,which can be achieved by first increasing the magnitude of the heading error and then decreasing it.So GTPG has a larger achievable time coverage than TPG by increasing tf,max, while tf,minin GTPG is the same as that in TPG.
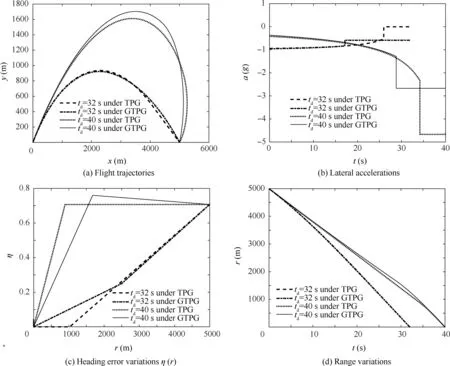
Fig.3 Results with different impact times.
Then, Table 5 is analyzed horizontally. It can be seen that when the magnitude of the initial heading error is small, the impact-time-control capacity of TPG and ITCG14almost disappears, while GTPG and ITCG2still retain some because an increase in the magnitude of the heading error is allowed at the beginning of the guidance.
4.1.2. Impact time control under different guidance laws
The simulation of the current case is carried out to investigate the evolution of the relevant states under different guidance laws. Set the desired impact time as td=33 s. The simulation results are shown in Fig.2. As seen in Figs. 2(a) and (d), the UAV intercepts the target at the specified time under individual laws. As Fig.2(b) shows, the acceleration under ITCG2finally converges to zero, while the accelerations under TPG and GTPG change monotonously in the first phase and remains constant after switching.As for ITCG14,the acceleration does not change much early, but more is required in the final phase. Fig.2(c) depicts the heading error variations during the engagement,which all converge to zero at impact. It is noted that under ITCG2, which cannot guarantee to meet the FOV constraint, the magnitude of the heading error grows at the beginning due to the same sign as acceleration. Under the other three guidance laws, the magnitude of heading error decreases monotonously, and the accelerations are always in the opposite direction of the initial heading error.These different behaviors cause the flight trajectory under ITCG2to be significantly different from those under the other three algorithms in Fig.2(a).
4.1.3. Impact time control with different impact times
The performance of TPG and GTPG is verified in two scenarios with desired impact times td=32 s and td=40 s.The simulation results are shown in Fig.3. From the trajectories plotted in Fig.3(a),it is found that a larger desired impact time leads to a more curved trajectory. With the same predefined impact time, the flight trajectories under TPG and GTPG are different due to the different switching states. The corresponding accelerations and heading errors are given in Figs. 3(b) and (c). It can be seen that under the two-phase guidance scheme,the UAV’s acceleration and heading error show visible switching action during flight, and there is no violation of the FOV and acceleration constraints. The accelerations under both algorithms change monotonically in the first phase and remain constant during the second phase. The evolution of accelerations is consistent with the theoretical analysis in Section 3.1.3.3 and 3.2.3.3. From Fig.3(c) we can see that the profile η r( ) consists of two straight-line segments as designed, and the heading error converges to zero at the time of impact. Under GTPG, the heading error is allowed to increase in the first phase, while it is always monotonically reducing under TPG. TPG corresponds to Case 1 when td=40 s,and corresponds to Case 2(with a =0 in the second phase)when td=32 s.Fig.3(d)indicates a successful interception at the predefined time.
4.1.4. Impact time control with autopilot lag
Simulations are carried out to demonstrate the robustness of feedback control.A first-order autopilot dynamics with a time constant τ =0.2 s is considered,and the desired impact time is set to be td=35 s.The simulation results are plotted in Fig.4.
Fig.4 Results of realistic implementation.As seen in Fig.4(a), the feedback form of TPG and GTPG drives the UAV to impact the target successfully with an acceptable impact time error. Fig.4(b) presents the guidance commands and the actual accelerations.

Table 6 Simulation parameters.
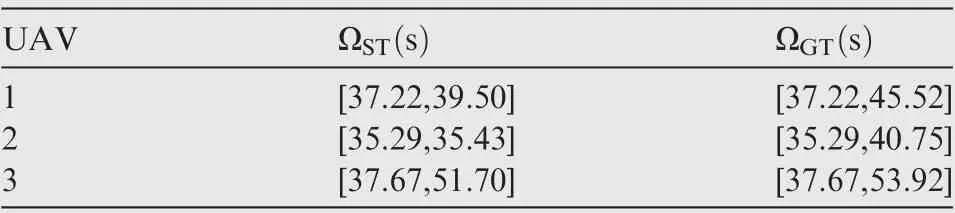
Table 7 Permissible sets of the impact times.
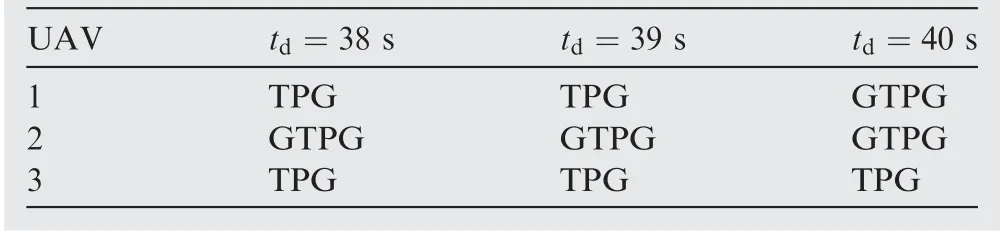
Table 8 Selected guidance laws.

Fig.5 Results of simultaneous attack.
4.2. Simultaneous attack for multiple UAVs
In this simulation,three UAVs at different locations engage in a salvo attack against a stationary target at the origin. An autopilot dynamics with a time constant τ =0.2 s is considered for UAVs to realize the instantaneous switching logic.The initial conditions of each suicide attack UAV are listed in Table 6,and the permissible sets of the impact times are tabulated in Table 7.
The intersection among ΩGTof individual UAVs can be acquired as[37.67,40.75]s,wherein three common impact times are selected as td=38 s,39 s and 40 s. According to tdand Table 7, appropriate guidance laws can be selected. It can be seen that when td=38 s,39 s UAV1 and UAV3 can be guided by TPG or GTPG,while UAV2 can only be guided by GTPG;when td=40 s UAV3 can be guided by TPG or GTPG, while UAV1 and UAV2 can only be guided by GTPG. The selected algorithms are listed in Table 8.
The simulation results are given in Fig.5. It can be seen from Fig.5(a)–(c) that three UAVs can hit the target at the same time.In Figs.5(d),only the flight trajectories of the three UAVs with td=39 s are shown to illustrate the entire interception process.
5. Conclusions
Without relying on any approximation or linearization, this paper proposes a two-phase guidance strategy for impact time control against a stationary target.As the single parameter for time control,the switching range is given in a simple analytical form without complicated calculations. The proposed two guidance laws can be regarded as proportional navigation guidance with a time-varying gain. During the engagement,the FOV constraint and the maneuver limit are satisfied. A feedback form of the guidance scheme is presented to keep robust to system delays. Also, the methodology can give the feasible interval of the impact times, providing a guide for the choice of the common impact time in a salvo attack. Simulations validate the relevant performance and analytic findings.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
 CHINESE JOURNAL OF AERONAUTICS2020年11期
CHINESE JOURNAL OF AERONAUTICS2020年11期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Event-triggered control for containment maneuvering of second-order MIMO multi-agent systems with unmatched uncertainties and disturbances
- Battery package design optimization for small electric aircraft
- Coactive design of explainable agent-based task planning and deep reinforcement learning for human-UAVs teamwork
- Adaptive leader–follower formation control for swarms of unmanned aerial vehicles with motion constraints and unknown disturbances
- Optimal video communication strategy for intelligent video analysis in unmanned aerial vehicle applications
- An aggregate flow based scheduler in multi-task cooperated UAVs network
